基于项目管理成熟度模型的创新工程质量目标控制研究
张小强, 丁玉乔
(中铁二院集团工程有限公司, 成都 610000)
在创新工程领域,新型轨道交通等创新项目的成功需要技术的不断创新,但是技术创新需要较高的费用和较长的周期。一个工程项目往往受到来自工程的工期、费用和质量三者共同影响,而这三者一般情况下都有着对立统一的关系,一个因素的改变往往会引起另外一个因素的改变。创新工程需要大量的新型技术,而新型技术往往造成工期和费用的不确定性,所以这三者的关系在创新工程中的矛盾更为突出。在创新工程中如何达到工期、费用和质量三者的最佳状态是工程建设需要不断考虑的问题。工程质量是否达标是象征一个国家和地区经济发展水平和生产力提高的重要标志和明显特征,在一些工程项目中,质量管理的重要性日渐突出,直接关系到工程的成败,关系到经济的发展,对工程质量管理的关注度也在逐渐提高。
目前,在实践过程中对于创新工程质量的优化控制较少。根据已有的研究,很多工程建设方面的研究往往着重于工期和费用两者之间的研究[1-2];注重工程技术和财务等方面的问题,对工程的质量不达标概率控制关注不够[3-4]。工程质量往往决定创新工程项目是否成功,因此,应重视对工期、费用和质量三者之间关系作用的研究[5-6]。由于缺少对项目质量的关注,所以一些工程实际完成质量目标低于计划完成的质量目标,使得最后延期交付或者是无法交付。因此,工程质量控制和优化也是工程管理极其重要的一个方面。
目前,创新工程项目的质量管理主要存在以下3个方面的问题[7]:①标准化程度较低,没有一个行业内通用的成熟的质量管理标准;②创新性较差,目前的质量管理往往还是根据以往的管理思想和经验步骤来进行管理,这种管理手段往往难以解决工程项目中不断出现的新的质量管理问题,从而使得质量管理效率低下;③缺乏数据的支持,正如上面所述很多的质量管理往往根据经验来进行管理,而没有数据方面的决策支撑与优化,使得最后的质量目标和计划目标相差甚远。基于以上问题,现借鉴项目管理成熟度模型(project management maturity model,PMMM)思路对质量控制进行研究。针对创新工程新问题,基于PMMM模型思想,通过考虑费用和工期对工程质量进行控制,使得实际质量目标低于计划质量目标的概率降低;建立质量控制模型,采用动态规划求解,同时通过对历史数据验证,确认了模型的有效性,一定程度上为质量控制提供了参考和借鉴。
1 质量管理相关研究
1.1 质量、工期和费用关系
影响创新工程的因素很多,包括质量、工期、成本、人力资源、风险及沟通等多方面[8],其中工程的工期、费用和质量是工程建设的3个决定因素,被称作“铁三角”。在实际的工程建设中往往无法同时达到三者的最优,为了保证质量目标的实现可能需要变更一些资源条件(包括工期和费用等),工程中质量与其他资源的关系如图1[3]所示。

图1 工程质量和费用、工期的关系[3]
在实际建设工程中,工程质量的提高通常需要工程工期和费用的支持。通常来说,工程工期和费用的缩减往往会导致质量的下降[9];相反,如果在原有基础上给工程追加一些资源,例如延长工期、增加费用等,一般情况下会使得工程的质量得到提高。基于此,本研究希望通过工期和费用两种资源的约束,对创新工程的质量进行优化。通过考虑如何增加工程的工期和费用资源使得工程的“质量不达标概率”最小,令工程质量可以达到最优。
1.2 质量管理方法
目前,质量管理大多集中在管理手段方面的研究而针对质量控制的研究较少。质量管理就是通过质量的目标制定、质量的实施方针以及各成员的职责履行等,并且通过管理中的控制、保证以及质量策划等,确保工程、产品和项目等质量的目标实现。目前质量管理途径与方法很多,例如汪霄和雷祖亮提出建立工程质量监督人员的评价模型,以此来督促管理人员对工程的监督[10];曾晖等和熊瑛等提出基于流程管理的质量管理方法[11-12],通过对流程进行分类以及构建流程化的质量管理模型对质量进行管理,从而可以从一个较为系统的角度来审视工程建设中的质量问题;乌云娜等通过将具体的工程质量管理问题与生物免疫机制相结合研究质量管理思想和方法,实现质量免疫系统的运行[13];杨高升等和郭延景等提出在政府项目中,工程主体可以运用系统动力学和演化博弈动态复制理念进行监督和管理[14-15];在供应链质量管理中,单汨源等通过社会责任和质量控制两个方面出发优化供应链质量管理[16];在工程企业和项目中,王琳娜等提出基于人工智能的质量管理方法,创新结合遗传算法和神经网络对质量水平进行预测,从而提高企业质量管理水平[17]。
影响工程质量的因素较多,使得工程质量问题逐渐复杂化[18]。传统的管理思路和管理方法已经难以适应新的管理问题。已有研究表明,工程质量受到多方面因素影响[19]。如果仅从工程质量方面出发进行研究往往难以克服不断出现的质量管理问题,故而需要从不同的视角进行质量管理问题研究[20-21],即工程工期和费用对工程质量的约束进行探讨。在创新工程中,工程受到技术影响较大,所以可以采用提高专利工法申请量[22]和设计施工总承包[23]等方法进行质量管理。
1.3 PMMM
PMMM最开始起源于美国卡内基梅隆大学软件工程研究所,该研究所最先基于软件项目研究,主要是针对软件过程的人员能力提升,经过几次修订后成为具有广泛影响的模型。之后,有多家组织及个人从项目管理的角度,参考模型和项目管理知识体系,使用不同的标准和依据,提出了各自的PMMM。目前PMMM被分为初始级、认知级、重用级、集成级和战略级5个阶段[24]。显然,成熟等级越高,工程的质量管理水平越强。
从PMMM考虑创新工程质量问题主要有以下3个优点:①PMMM可以将质量管理问题很好地融合在框架内进行研究;②PMMM质量问题研究主要是基于以往的历史数据,使得质量问题研究有数据支撑;③已有的PMMM中已经充分考虑过质量管理问题领域的基本过程,具有良好的适配性。
2 质量控制模型
2.1 假设与定义
虽然在创新工程项目中,质量与时间、费用有因果关系,但影响工程质量的关键因素很多。因此,在研究质量、时间、费用三者关系时,做出以下假设。
假设1:在工程项目的开始阶段,工程质量与时间、费用成线性因果关系,即增加时间或费用,可以确保工程质量,降低质量风险。
假设2:在工程项目的中期,当工程质量是可逆时,增加时间或费用可维持或提高质量。当工程质量不可逆时,可能增加时间或费用就不一定能维持或增强质量。
假设3:在工程项目的后期,工程质量与时间、费用成非线性因果关系,增加时间或费用就不可能维持或增强质量。
本研究主要考虑的是工程质量可逆的前期和中期,即在此阶段增加时间和费用的投入,可以降低质量风险。
2.2 质量模型
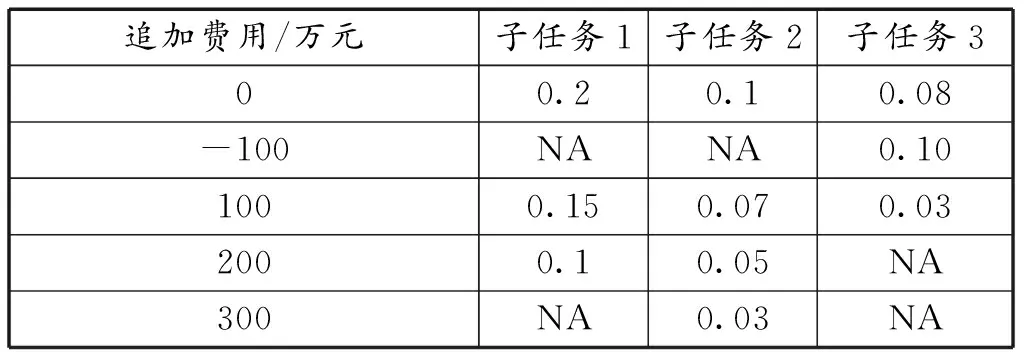
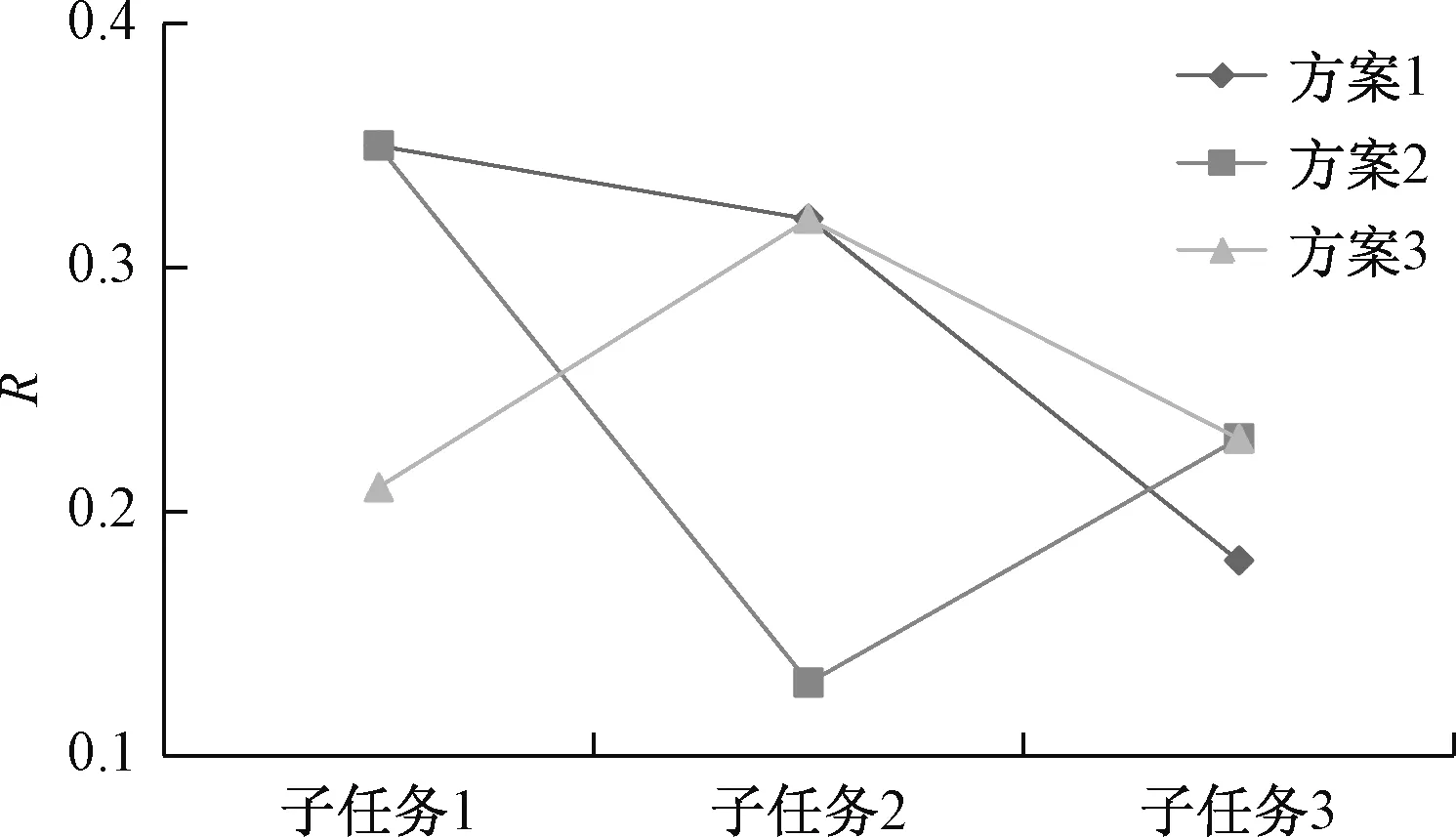
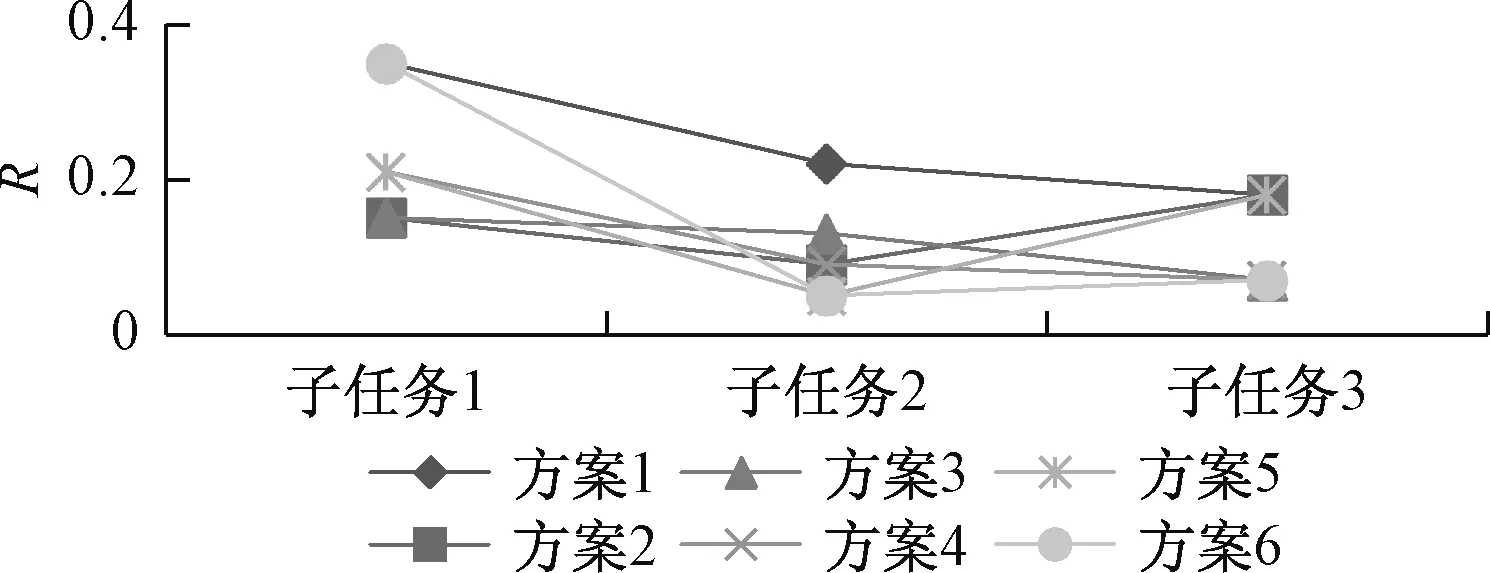
设ri为没有实施质量控制时子任务i的实际完成质量低于计划完成质量的概率,即ri=P(qi 设工程质量不达标概率为R,没有实施质量控制时工程实际完成质量目标低于计划完成质量目标的概率R=P(Q 如果工程有n个子任务,则工程质量不达标概率[25]为 (1) 整个工程的质量不达标概率目标为 (2) 通常来说工程的质量不达标概率与费用、时间的投入有负相关的关系,设在子任务i上增加费用投入ci,增加时间投入di,投入前后的质量不达标概率分别为ri(0,0)和ri(ci,di),分别记为r′i和ri。 投入前后质量不达标概率和时间费用之间的关系为 ri=gi(r′i,ci,di) (3) 式中,gi取决于任务i本身组织的优化能力。 假设追加的总费用为Cmax,并且工程有n个子任务,如果Cmax在n个任务之间中有e种分配方案,对于其中第h种分配方案,每个任务得到的追加投入分别为c1h,c2h,c3h,…,cnh相应各个子任务的质量不达标概率为r1h,r2h,r3h,…,rnh。 假设管理追加的总时间为Dmax,并且工程有n个子任务,如果Dmax在n个任务之间中有l种分配方案,对于其中第p种分配方案,每个任务得到的追加时间投入分别为d1p,d2p,d3p,…,dnp相应各个子任务的质量不达标概率为r1p,r2p,r3p,…,rnp。 设U和V分别是可以选择的投入方案以及相应的状态。 考虑成本进度,多目标优化模型为 (4) 运用动态规划求解,假设追加的费用投入为α,时间投入为β,对于其中的第i个子任务追加投入为αi和βi,相应各个子任务的质量不达标概率为f(αi,βi),存在以下4种情况: 1)如果该工程的所有子任务都没有追加投入,则此时总的追加费用和时间投入α0=0,β0=0,设此时的工程质量不达标概率为f0(α0,β0)。 2)如果该工程只有子任务1得到追加投入而其他子任务没有得到追加投入,那么此时总追加费用投入为α1(0≤α1≤Cmax),总追加时间投入为β1(0≤β1≤Dmax),相应的此时只有子任务1的质量不达标概率发生变化,其余的子任务质量不达标概率都没有变化,设此时的工程质量不达标概率为f1(α1,β1)。 3)如果子任务1,2,3,…,k(k 4)如果所有的子任务都得到了追加投入,那么此时的追加费用总投入为αn(0≤αn≤Cmax),追加时间总投入为βn(0≤βn≤Dmax),此时所有子任务的质量不达标概率都发生变化,设此时的工程质量不达标概率为fn(αn,βn)。 求解如下: (5) 式中,α=β=α0=β0=0,α′i=ri(α0,β0)。 2)f1(α1,β1)=min(1-{1-f0[(α1-c1)+(β1-d1)]δ1(c1,d1)}) (6) 式中,δ1(c1,d1)=[1-r1(c1,d1)]/[1-r1(c0,d0)]。 3)fk(αk,βk)=min(1-{1-fk-1[(αk-ck)+(βk-dk)]δk(ck,dk)}) (7) 式中,δk(ck,dk)=[1-sk(ck,dk)]/[1-sk(c0,d0)]。 中国某段新型轨道移动供电项目被某企业承包,该项目采用目前最新的技术工艺,属于目前国内首创的技术,并且零部件结构还在不断改进。该项目主要是对原有轨道进行更换,即新型轨道采用钢铝融合导电轨,采用革命性的新工艺制造,整体性能大幅度提高,满足最新的轨道要求,增加轨道的耐磨性。该项目主要有贴边和打磨等生产环节和材料物理性能检测、材料化学性能检测和电性能检测等试验环节,本研究主要针对研发试验环节。 由于该轨道项目采用新型技术,会给工程的质量带来不确定性,所以在工程实施过程中会涉及工期和费用的变动;同时由于该段轨道更换只能夜间进行,为了保证工程质量,在项目实施过程中需要增加人员等进行弥补,而人员的增加往往也会涉及工期和费用的变动,所以本研究以该项目为实例来验证模型的有效性。 基于PMMM思想,根据该新型轨道工程项目研发试验环节的历史数据,得出子任务在不同的追加费用下的质量不达标概率程度。其中Cmax=400万元,在最开始没有追加费用投入的情况下,3个子任务的质量不达标概率分别为0.2、0.1和0.08,同时表1给出了不同追加费用情况下的备选方案。 表1 子任务追加费用后质量不达标概率 表2根据以往的历史数据,得出子任务在不同的追加时间下的质量不达标概率程度。同样地Dmax=4个月,在最开始没有追加投入时间的情况下,3个子任务的质量不达标概率分别为0.15、0.12和0.1,表2给出了不同追加时间情况下的不同备选方案。 表2 子任务追加时间后质量不达标概率 在没有追加投入的情况下可分为3种方案,为了方便计算,考虑追加投入的时间和费用一致。 1)在最初工程没有追加投入费用的情况下,即追加费用为0,工程的最初质量不达标概率分别为0.2、0.1和0.08;同时在没有追加投入时间的情况下,即追加投入时间为0,工程的最初质量不达标概率为0.15、0.12和0.1,所以此时工程的质量不达标概率为 2)子任务分别追加投入0、1、-1(包括时间和费用),即子任务1没有追加投入,子任务2追加投入1个月和100万元,子任务3减少投入1个月和100万元,此时的工程质量不达标概率为 3)子任务分别追加投入1、0、-1(包括时间和费用),即子任务1追加投入1个月和100万元,子任务2没有追加投入,子任务3减少投入1个月和100万元,此时的工程质量不达标概率为 从以上3种方案的计算结果可以看出,3种方案的质量不达标概率分别为0.584 26、0.564 565和0.525 526,方案3的质量不达标概率最小,即子任务1追加投入1个月和100万元,子任务2没有追加投入,子任务3减少投入1个月和100万元,此时每个子任务在不同方案下的质量不达标概率如图2所示。 图2 不同方案下子任务质量不达标概率 从结果可以看出方案3相较于其他两个方案质量不达标概率更小,但是方案3的质量不达标概率R=0.525 526,此时整个工程的质量不达标概率仍然比较大,所以可以考虑不断向工程追加投入。 在考虑追加投入时,根据已有历史数据,分为以下4种情况,即原始方案没有追加投入、追加部分任务的投入、追加全部任务的投入和随机追加投入。 3.3.1 原始方案 工程没有追加投入,即每个子任务的追加投入为0,此时的工程质量不达标概率为 3.3.2 追加部分任务投入 将全部追加投入分配给子任务1和子任务2,即分别得到200万元追加费用和2个月的追加时间,此时的工程质量不达标概率为 3.3.3 追加全部任务投入 1)将全部追加投入分别分配给3个子任务,分别得到200万费用和2个月时间的追加、100万费用和1个月时间追加,以及100万费用和1个月时间追加投入,此时的工程质量不达标概率为 3.3.4 随机追加投入 1)将全部追加投入随机分配给3个子任务,分别得到100万费用和1个月时间的追加、300万费用和3个月时间追加,以及0费用和0时间追加投入,此时的工程质量不达标概率为 2)将全部追加投入随机分配给3个子任务,分别得0费用和0时间的追加、300万费用和3个月时间追加,以及100万费用和1个月时间追加投入,此时的工程质量不达标概率为 以上方案中,不同子任务的质量不达标概率如图3所示。 图3 追加投入后不同方案下子任务质量不达标概率 由计算结果可知,方案3即3个子任务分别得到200万费用和2个月时间的追加、100万费用和1个月时间追加,以及100万费用和1个月时间追加投入,工程的整体质量不达标概率最小为0.312 265,同时从图3也可以看出,该方案下各子任务的整体质量不达标概率最小;其次就是方案4,即3个子任务分别得到100万费用和1个月时间的追加、200万费用和2个月时间追加,以及100万费用和1个月时间追加投入,此时工程质量不达标概率为0.331 423。这两个方案都是将全部追加投入分别分配给3个子任务,也说明了这一追加投入方法可以使得工程质量不达标概率降到最低,在后期的工程实践中也验证了该方法的科学性。 在实际的工程质量管理中,为了保证质量目标的达成,应该将追加投入分配给尽可能多的项目子任务,这样可以保证工程项目质量不达标的概率最低;针对轨道交通这一类创新工程具有更为重要的意义,这类项目周期长成本高,通过协调费用和周期的追加,使得创新工程的质量效果最大化,降低创新质量不达标的风险。 值得注意的是在创新工程项目中,除了费用和工期会影响工程质量以外,技术、沟通和环境等因素都会直接或间接影响工程质量,应该加强项目的实施管理; 同时本文只考虑将质量作为优化目标,在以后的研究中,应该把费用和工期也作为优化对象,综合优化是下一步的研究方向。2.3 考虑费用及工期追加
2.4 优化模型
2.5 模型求解
3 应用举例
3.1 项目概况
3.2 没有追加投入

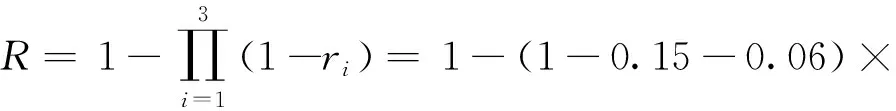
3.3 增加追加投入
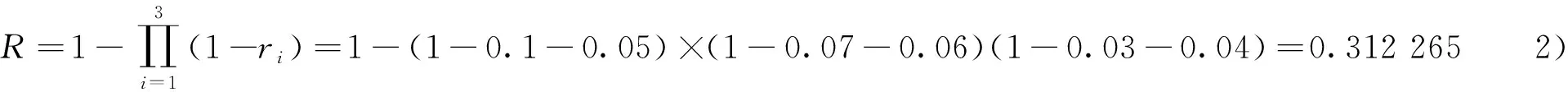
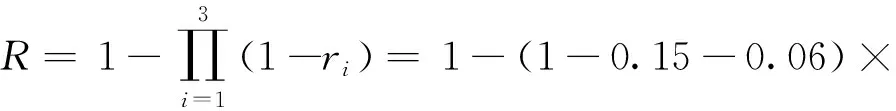
4 结语

