基于Lagrange插值多项式拟合的力学系统的变分积分子*
孔新雷 杨雪
(北方工业大学理学院,北京,100144)
引言
Lagrange系统是由Euler-Lagrange方程

所描述的一类力学系统,其中x=(x1,x1,…,xn)代表位 形 流形M的局部坐标 ,L(x,ẋ)是系统的Lagrange函数,一般为系统的动能和势能之差.如果进一步考虑非保守力,那么Euler-Lagrange方程的形式会发生些许变化[1],但这种情况在本文中暂不研究.当系统(1)是一组非线性微分方程时,对其解析求解是非常困难甚至是不可能的,因此需要借助于数值手段,通常是采用经典差分格式,用差分方程代替微分方程实现数值求解.
然而,人为地采用经典差分格式离散系统的运动方程,不可避免地会破坏连续系统具有的几何结构,引入不必要的数值耗散.因此,在“数值算法应尽可能地保持原问题的本质特征”[2]的指导原则下,针对系统(1),人们提出并设计了保结构算法[2,3].较早的保结构算法主要是保辛差分格式 .借助于Legendre变换,Euler-Lagrange方程可以转化为Hamilton正则方程,而基于Hamilton系统的辛结构,利用生成函数法可以构造系统的保辛差分格式[2].变分积分子是另外一种构造思路的保结构算法.考虑到Euler-Lagrange方程可以由Hamilton原理诱导,仿照这一连续情形,在对系统(1)构造数值算法时可以先离散Hamilton原理,由离散后的Hamilton原理可以导出离散Euler-Lagrange方程.作为离散变分原理的产物,离散Euler-Lagrange方程在作为数值差分格式时,真实地继承了连续系统具有的几何特性,不仅是自然保辛的,而且满足Noether定理进而保持系统的动量[4,5].自然简便的构造方式和优越显著的计算性能,使得变分积分子迅速发展,不仅局限于系统(1),对于非保守系统[5,6]、非光滑系统[7]、完整和非完整约束系统[8-10]、Birkhoff系 统[11-13]、连续介质力学[14,15]、随机系统[16,17]等都可以构造系统的变分积分子,进行高效的数值模拟仿真.
本文结合局部路径拟合[18,19]方法提出一种新的变分积分子的设计构造方式.考虑到变分积分子的经典构造过程最终归结为计算离散Lagrange函数的偏导数,本文先对相关涉及到的偏导数进行解析计算,发现一个新的依赖于Euler-Lagrange方程的积分随之产生.在对该积分实现科学有效的近似之后,离散Lagrange函数的偏导数就转化为连续Lagrange函数关于速度变量的偏导数,这样就省略了利用经典求积公式计算离散Lagrange函数的过程.因此,这种新的构造方式不仅让最终得到的差分格式仍然继承了变分积分子特有的优越计算性能,而且显著地简化了其构造过程,特别是对于高阶精度的变分积分子.
1 变分积分子
如引言中所述,Lagrange力学系统是由Euler-Lagrange方程

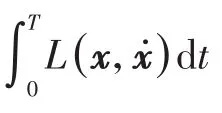
变分积分子是一类特殊的数值差分格式.与经典差分格式不同,构造力学系统的变分积分子,出发点不是直接离散运动方程,而是离散能够诱导运动方程的变分原理.
具体到Lagrange力学系统,首先考虑离散Lagrange函数
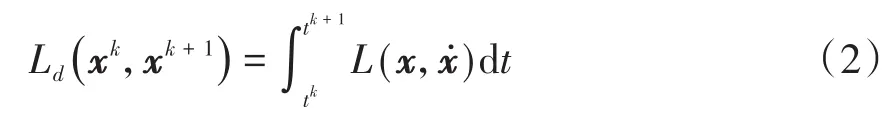
其中,xk是x(tk)的近似,τ=tk+1-tk是选定的时间步长.这样
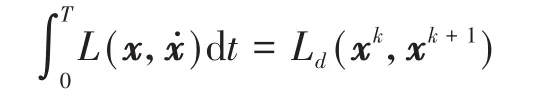
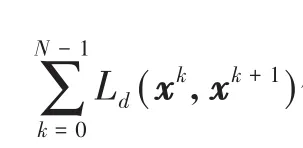

进 一 步 注 意 到δx0=δx(0)=0 以 及δxN=δx(T)=0,可得离散Euler-Lagrange方程
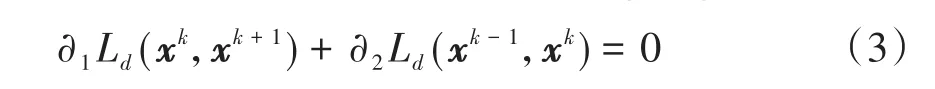
写成分量形式为

当∂2Ld满足非退化条件时,离散Euler-Lagrange方程(3)就确定了差分格式
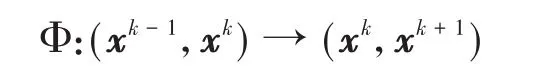
这种由离散变分原理所得到的数值算法Φ就被称作变分积分子.独特的构造方式避免了人为的离散运动方程所带来的数值耗散,使得变分积分子能够真实地继承连续系统的解所具有的几何性质,例如保辛性,即算法Φ满足Φ∗Ω=Ω,其中微分形式
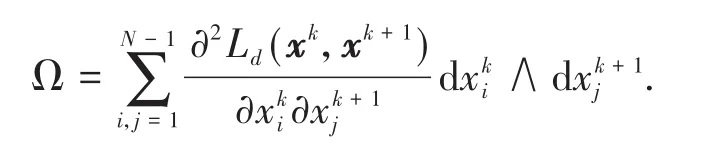
另外,与连续情形类似,当离散Lagrange函数Ld进一步满足李群作用不变性时,算法Φ还保持动量(映射)不变.根据后误差分析理论,变分积分子所表现出的优越计算性能,如高精度、长时间稳定、保持系统守恒量等,都与其保结构特性有着直接关系.当力学系统受到若干完整约束,即位形坐标x=(x1,x1,…,xn)满足代数方程组
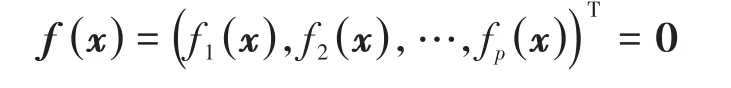
时,借鉴上述先离散后变分的思想,并结合Lagrange乘子法,同样可以构造完整约束系统
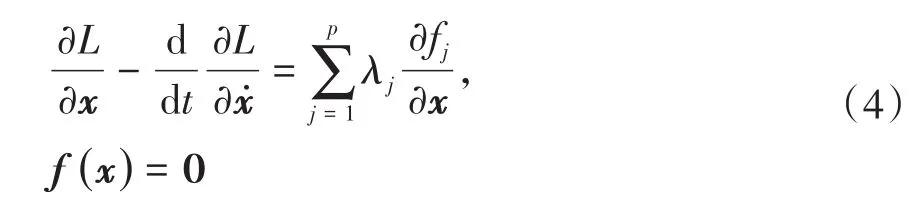
的变分积分子

其中,
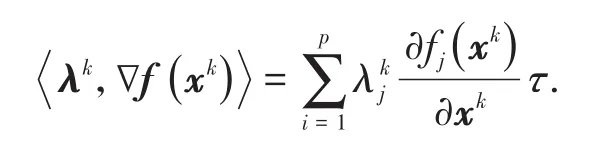
值得注意的是,如果引入扩展的离散Lagrange函数
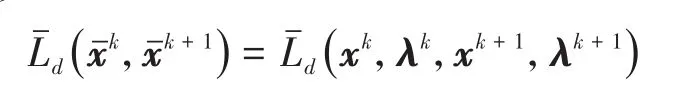

或

那么,方程组(5)与以Lˉd(xˉk,xˉk+1)为离散 Lagrange函数的离散Euler-Lagrange方程

等价[5].
2 基于Lagrange插值多项式拟合的力学系统的变分积分子
根据离散Euler-Lagrange方程(3)的形式可知,构造力学系统的变分积分子最后归结为计算离散Lagrange函数的偏导数——∂1Ld和∂2Ld.为了计算这些偏导数,首先引入自由变量μ,在实际计算偏导数时μ可以代表或.由于离散Lagrange函数

那么,


进一步地,利用分部积分公式可得

在上式中,记



同理,当考虑时间区间[tk-1,tk]时,
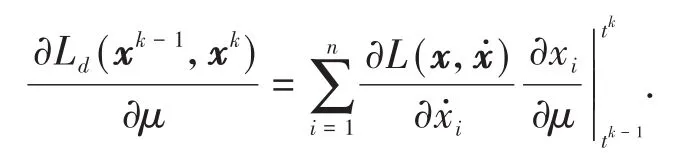
假设在时间区间[tk,tk+1]内,
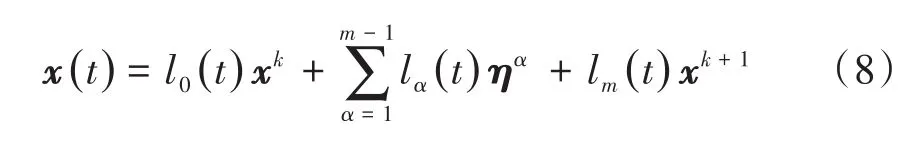
其中,

而ηα=(,,…)T是拟合轨迹x(t)在离散时间结点处的值,并且满足Euler-Lagrange方程,那么根据x(t)的表达式可以计算ẋ(t)、ẍ(t)以及

这样,由(7)式可得
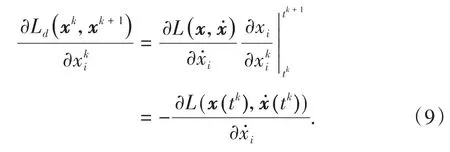
同理,当考虑时间区间[tk-1,tk]时,

利用(9)式和(10)式,联立方程组


其中,i=1,2,…,n,α=1,2,…,m-1,则首先由方程(12)可求得ηα=ηα(xk,xk+1),平行地,当时间区间为[tk-1,tk]时,ηα=ηα(xk-1,xk);然后将求得的ηα代入x(tk)和ẋ(tk),并进一步带入(9)式和(10)式,那么方程(11)就转化关于xk-1、xk和xk+1的代数方程,即变分积分子Φ:(xk-1,xk)→ (xk,xk+1).
注1:单个步长区间[tk,tk+1]内,在对局部轨迹x(t)进行插值拟合时,除了Lagrange插值多项式(8)之外,还可以采用其他的插值方式,例如二项插值

式可得

代入偏导数∂1Ld和∂2Ld,同样可以得到

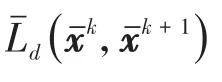
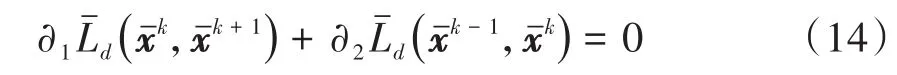
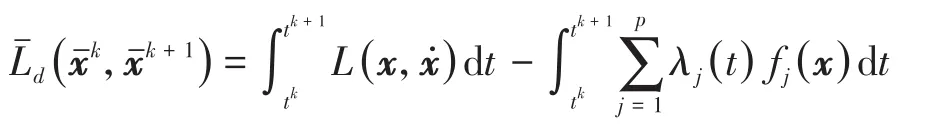
对应地


记
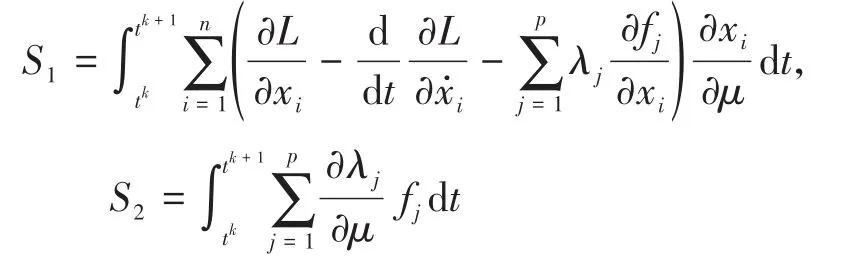

平行地

在时间区间[tk,tk+1]内,如果局部轨迹x(t)和λ(t)都按照Lagrange插值多项式进行拟合,则最终可得
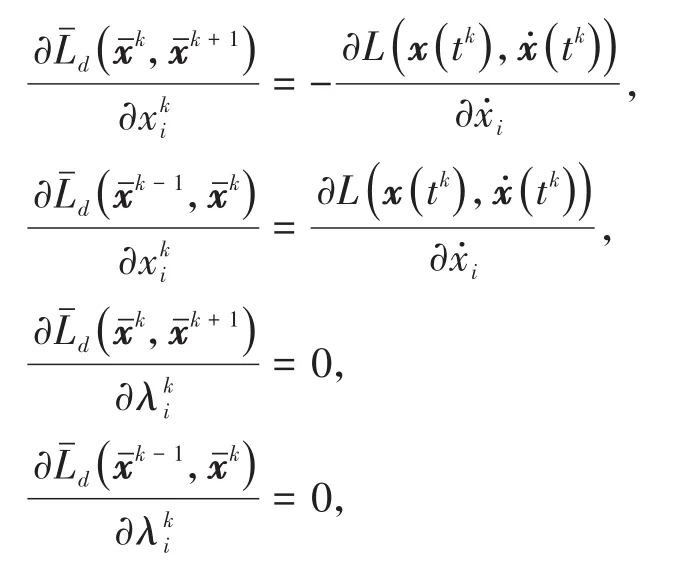
而方程(14)则随之变为
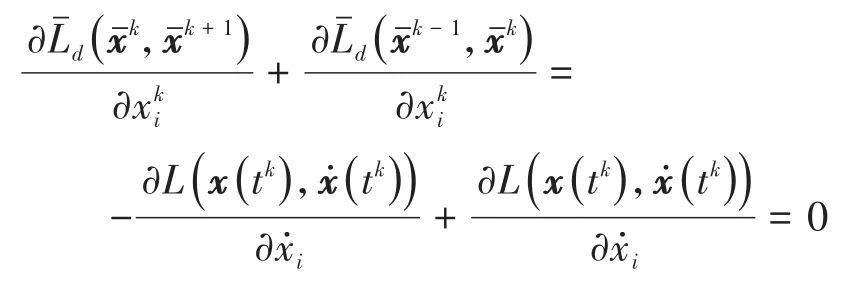
3 数值算例
3.1 算例1—简谐振子
考虑简谐振子方程

在时间区间[tk,tk+1]内,令
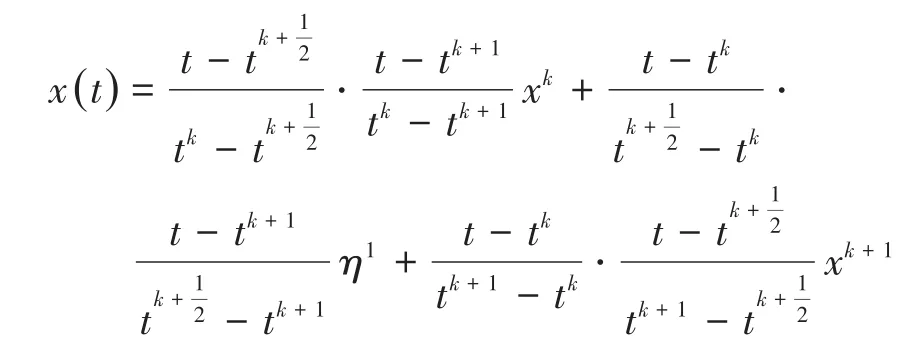
则求导可得

在t=tk+τ/2处,由Euler-Lagrange方程,即系统运动方程(15)成立可得
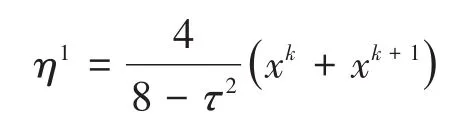
将η1带入ẋ(t)相应可得

那么,由离散Euler-Lagrange方程(11)可得

迭代算法(16)就是利用新的构造方法针对简谐振子方程(15)设计的变分积分子.假定系统(15)的初值为x(0)=ẋ(0)=1,以τ=0.1为时间步长,利用差分格式(16)对系统进行数值求解,则对应的数值解如图1所示.显然,该差分格式非常精确地数值模拟了简谐振动,在图示的尺度下,方程的数值解和精确解所对应的曲线完全重合,无任何差别.
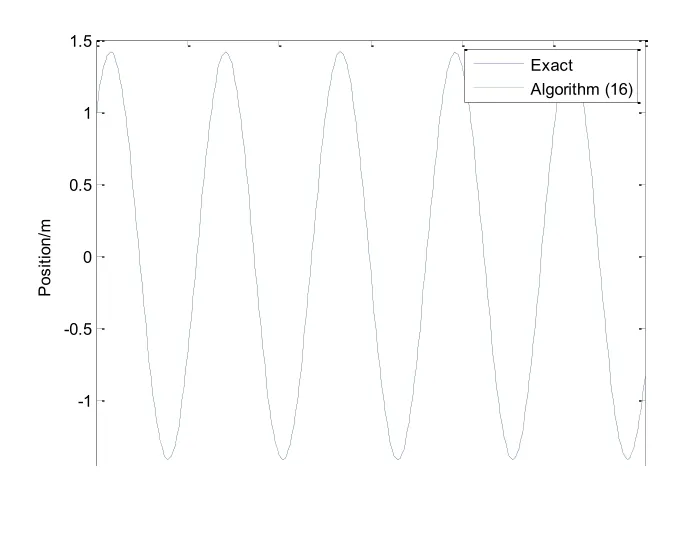
图1 方程(15)的精确解与通过差分格式(16)算得的数值解对照Fig.1 Comparison between the exact solution and the numerical solution computed by algorithm(16)for equation(15)
除了有效性得以验证之外,由图2可以非常直观地看到,差分格式(16)也非常真实地模拟了系统的能量,所计算出的数值能量曲线呈现出长时间的守恒行为,且能量误差始终保持在有界的范围内.保持保守系统的守恒量,这是变分积分子特有的计算优越性,因此,图2中的数值结果也验证了通过局部路径拟合方法构造的变分积分子继承了经典变分积分子优越的计算性能.实际上不仅如此,在同阶精度的情况下,借助新方法得到的变分积分子具有更小的误差.

图2 由差分格式(16)算得的系统(15)的数值能量曲线Fig.2 The numerical energy curve of system(15)computed by algorithm(16)
为了验证这一事实,采用经典求积公式—中点格式—逼近(2)式中的积分可得与系统(15)对应的离散Lagrange函数

根据离散Euler-Lagrange方程(3)可得经典变分积分子

差分格式(16)和差分格式(17)尽管都是具有二阶精度的数值算法,然而由表1中数据可以直观地对比出差分格式(16)具有更小的局部误差和整体误差.

表1 不同时刻差分格式(16)和差分格式(17)的误差对比Table 1 Local errors of numerical solutions and energies at different times computed with algorithms(16)and(17)respectively
当然,如果单个步长区间[tk,tk+1]内的离散结点取得更加密集,那么可以得到更加精确的差分格式.例如,在时间区间[tk,tk+1]内,如果设
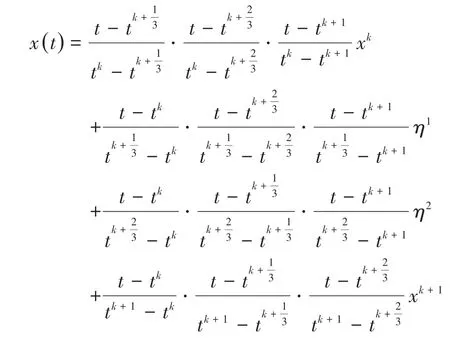

对应地

代入离散Euler-Lagrange方程(11)可得差分格式

又例如,如果在[tk,tk+1]内再多取一个结点,即令
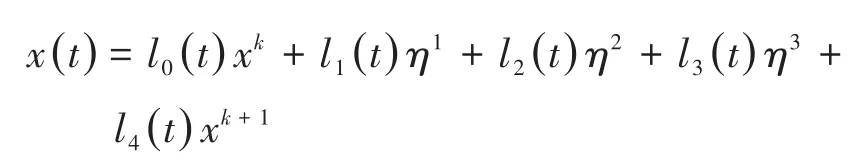
则最终可得变分积分子
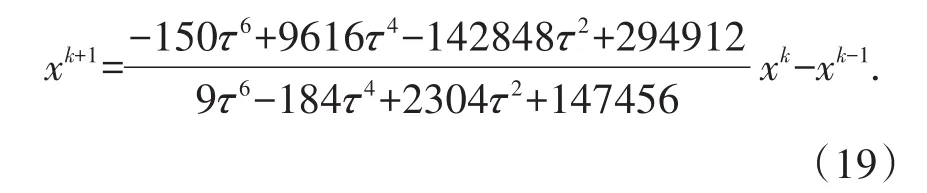
如表2中数据所示,差分格式(18)和差分格式(19)较之差分格式(16)具有更小的误差.内部结点选取得越密集,得到的数值算法越精确,这一规律与经典构造过程中愈加复杂的积分逼近格式诱导愈加精确的变分积分子相一致.
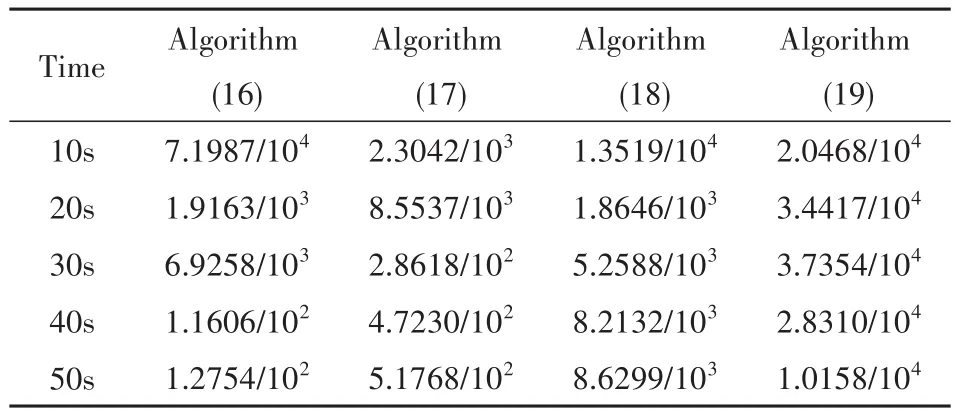
表2 不同时刻差分格式(16-19)的数值解误差对比Table 2 Local errors of numerical solutions at different times computed with algorithms(16-19)respectively
3.2 算例2—单摆
单摆运动方程

也可以等价地表述为Euler-Lagrange方程,对应的Lagrange函数为

在单个步长区间内如果只选取一个结点,那么对于系统(20)可得如下方程组

或
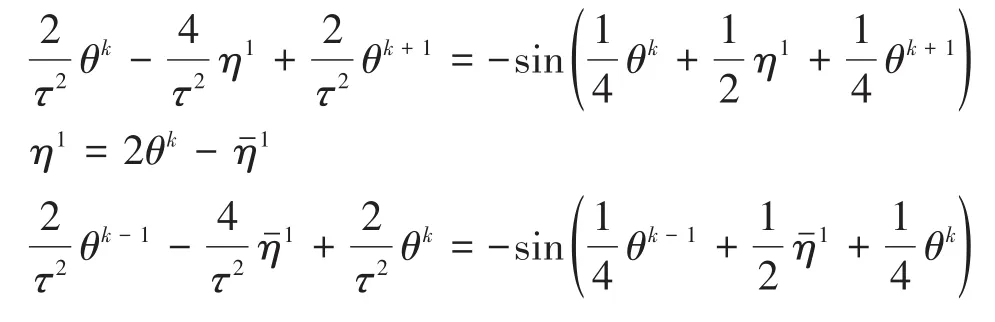

其中方程组(21)是基于Lagrange插值(8)诱导得来,而方程组(22)是基于二项插值(13)得来.隐式地求解方程组(21)或(22)均可得变分积分子(θk,θk+1)= Φ(θk-1,θk).利用两种差分格式算得系统(20)在相空间中的数值轨迹和数值能量如图3所示.显然,两种差分格式不仅有效地模拟了系统的运动,而且非常真实地反映了系统能量守恒.

图3 由差分格式(21)和(22)分别算得的系统(20)在相空间中的数值轨迹(a)和数值能量曲线(b)Fig.3 Numerical orbits in the phase space(a)and numerical energy curves(b)of system(20)computed by algorithms(21)and(22)respectively
3.3 算例3—匀速圆周运动
单位质量的质点在二维平面内做匀速圆周运动,其运动方程可以表述为
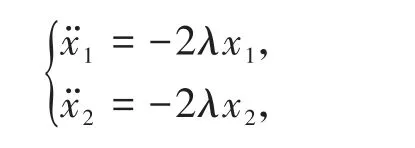
其中位形坐标(x1,x2)满足约束条件x21+x22=1.基于Lagrange插值多项式(8),可得该完整约束系统的变分积分子

式(23)构成了一个具有二阶精度的隐式差分格式.
4 结论
本文结合局部路径拟合方法提出了一种新的力学系统变分积分子的设计方式.数值结果表明,这种基于局部路径拟合的构造方法不仅让最终得到的数值算法仍然继承了变分积分子特有的优越计算性能,而且显著地提高了算法的精度.另外,这种构造方法不仅适用于自由无约束系统,而且适用于完整约束系统.

