高强轻质重整加热炉管板结构优选与优化分析
丁宇奇 成佳浩 芦 烨 王学勇 叶碧涛 谢 清 卢 宏
(东北石油大学机械科学与工程学院)
重整加热炉是连续重整装置的主要设备之一,随着重整装置大型化的发展,对流段中间管板作为炉内关键的支撑部件也从结构上趋于大型化,因而对其强度和可靠性的要求也日益提高[1~3]。优化设计出高强度轻质量的对流段中间管板, 对于重整加热炉大型化的发展具有重要意义。 杨良瑾等从理论上提出管板优化设计的途径: 在一次结构法基础上采用GB/T 151—2014《热交换器》 中的方法计算管板应力或用有限元数值分析法计算管板应力,以3[σ]作为控制值可获得较薄的管板计算厚度,得到经济合理且安全可靠的设计结果[4]。 薛明德和吴强胜以对流换热条件下的换热器管板为研究对象,使用有限元分析方法得出管板过厚会引起过大的热应力的结论,对于各种以温度载荷为主的换热器应注意选择合理的管板厚度[5]。 王思莹和李卫红采用ANSYS有限元软件模拟管壳式换热器的管板厚度对管板和壳体连接处应力的影响,发现在温度载荷下管板厚度对应力数值有显著影响[6]。 蔡建光等使用有限元模拟计算方法对直线形和波浪形两种加筋肋结构的管板分别取不同区域进行应力分析,发现波浪形加筋肋管板的应力分布比直线形加筋肋管板的更为均匀[7]。 王战辉等以换热器管板为研究对象,利用有限元分析软件对管板进行了应力和热-应力耦合分析, 并对管板进行结构优化分析, 改进后管板质量减轻了38.5%[8]。Masanori Ando等通过模拟非均质管板结构在周期性热瞬变下的强度,评估了管板在循环热载荷作用下的失效形式[9]。 Liu M S等研究了传热设备管板温差引起的热应力,采用有限元法计算温度场和应力场,提出了减小或消除管板热应力的措施[10]。 Du Y N以换热器管板为研究对象,使用极限荷载法和弹塑性法,优化管壁厚度后进行了塑性倒塌评估,实现了管板轻量化[11]。 Liu J Y采用有限元法建立了由管板、管槽、部分管壳组成的U形管换热器的三维有限元模型,对管板的最小厚度进行了优化计算,使管板厚度减薄31%[12]。
通过上述分析可知,国内外学者主要采用理论计算和数值模拟的方法,通过控制管板厚度实现管板的优化,但多是以换热器管板或是换热设备的管板为研究对象,与重整加热炉内的管板相比还有很大区别。 因此对加热炉内不同结构管板进行优选和优化设计, 得到高强轻质的管板结构,对重整加热炉管板结构的大型化具有重要意义。 为此,笔者以直板形、波浪形和直板加筋肋形3种不同结构对流段中间管板为研究对象, 采用有限元计算方法对比了3种管板的应力分布和最大应力出现的位置,优选出最佳管板结构;再以此管板结构为研究对象, 以管板质量为目标函数、管板厚度为设计变量,对管板结构进行优化分析,科学合理地确定相关设计参数,有效提高管板的承载能力,对高强轻质管板的设计具有重要意义。
1 基于三维模型的对流段中间管板有限元模型的建立
1.1 几何结构和受力特点
笔者研究了3种不同形状的管板结构, 分别是直板形、波浪形和直板加筋肋形对流段中间管板。 图1所示为波浪形对流段中间管板结构,该管板材料为ZG35Cr25Ni12, 常温下的屈服强度为678MPa; 管板排数为5排、 温度由下而上依次为791、737、689、642、593℃; 管 板 开 孔 直 径 为176mm、 孔中心距203.2mm、 上下排孔中心距为203.2mm,管板长度2 750mm、高度867mm、厚度25mm,筋板长度2 570mm、宽度120mm,吊耳厚度25mm。
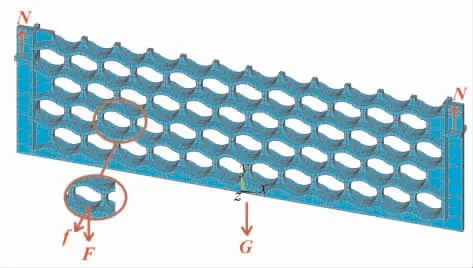
图1 波浪形对流段中间管板结构
由图1标出的管板受力方向可以看出, 管板整体结构受到自身向下的重力G, 在两端吊耳处受到竖直向上的支撑力N, 管板局部开孔位置处承受炉管和管内介质带来的竖直向下的压力F,在炉管与管孔接触的位置受到炉管轴向膨胀引起的水平摩擦力f。
1.2 有限元模型的建立
建立波浪形对流段中间管板整体结构有限元模型如图2所示, 该模型可以描述管板整体的实际结构,管板的网格划分采用六面体,并且经过多次网格无关性的验证,确保了管板计算的准确性。 为了详细分析管板的应力分布情况,设计两条管板应力评价路径:
a. 考虑管板实际安装状况,管板两端吊耳支撑整个对流管板重量和管孔内炉管及其介质重量,是管板容易发生危险的位置,因此在吊耳处设置评价路径A-A;
b. 管板开孔承受来自炉管及管内介质重量和炉管轴向膨胀的摩擦力作用,因此在管板开孔位置设置评价路径B-B。
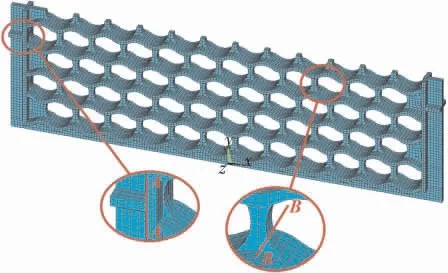
图2 波浪形对流段中间管板有限元模型
2 对流段中间管板应力分析与强度评定
2.1 应力评定方法
对流段中间管板所受静载荷+摩擦载荷时,根据SH/T 3036—2012《一般炼油装置用火焰加热炉》[13]的规定,设计温度下管板最大许用应力应不超过下列各值:
a. 抗拉强度的1/3;
b. 屈服强度(0.2%残余变形)的2/3;
c. 10 000h产生1%蠕变时的平均应力;
d. 10 000h发生断裂的平均应力。
对流段中间管板各部位的一次局部薄膜应力σ2、 一次薄膜应力+一次弯曲应力σ3, 按照JB 4732—1995(2005年确认)《钢制压力容器——分析设计标准》[14]给出的应力分类与强度评价条件为:一次局部薄膜应力σ2≤1.5[σ],一次薄膜应力+一次弯曲应力σ3≤1.5[σ]。
2.2 计算结果
波浪形对流段中间管板的整体变形和等效应力分别如图3、4所示,整体危险路径A-A的线性化曲线如图5所示, 管板危险路径处的应力计算结果列于表1。
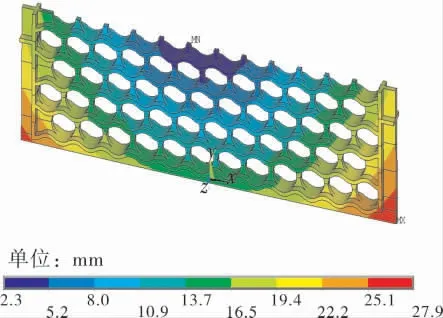
图3 波浪形对流段中间管板的整体变形
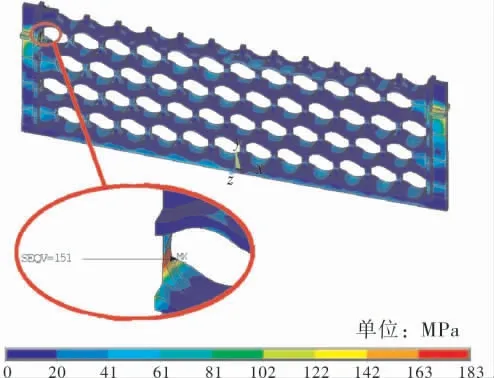
图4 波浪形对流段中间管板的等效应力

图5 波浪形对流段中间管板整体危险路径A-A的线性化曲线
由图3、4可看出, 波浪形对流段中间管板的整体变形为2.3~27.9mm,最大等效应力(183MPa)出现在吊耳处。 由表1可知,波浪形对流段中间管板吊耳处的σ2=68MPa,开孔处的σ2=56MPa;吊耳处的σ3(129MPa)大于开孔处的σ3(108MPa),更接近强度条件(1.5[σ]=162MPa),并且是两个危险路径处(图5)的最大应力值,因此该管板的吊耳处比较危险。而管板整体和开孔处的σ2、σ3均在安全范围内,满足强度要求,说明该管板结构能够安全工作。

表1 波浪形对流段中间管板危险路径处的应力计算结果
3 不同对流段中间管板的结构优选
3.1 结构特点
对直板形、波浪形和直板加筋肋形对流段中间管板进行分析,三者在管排数目、开孔数目、开孔直径、 吊耳的高度以及结构尺寸等方面均相同,但结构形状不同。 直板形对流段中间管板结构的显著特点是筋板形状为直线形,吊耳位于管板两端上侧的位置,上下排之间开孔的位置采用相互交错的形式,且孔心距受到开孔直径和筋板厚度的影响;直板加筋肋形对流段中间管板的结构特点是将筋板加宽,增大了炉管与筋板的接触面,有效地提高了筋板的强度;波浪形对流段中间管板在筋板设计上与上述二者有很大区别,采用波浪线的形式构建管板的形状,缩短了上下排管孔之间的中心距,进而使得管板的整体高度较低,结构更加紧凑[15]。
3.2 计算结果分析
图6为直板形对流段中间管板的等效应力分布, 图7为直板加筋肋形对流段中间管板的等效应力分布。 由图6、7可看出,直板形和直板加筋肋形对流段中间管板的应力分布几乎一样,这主要是因为二者的筋板结构均为直线形。
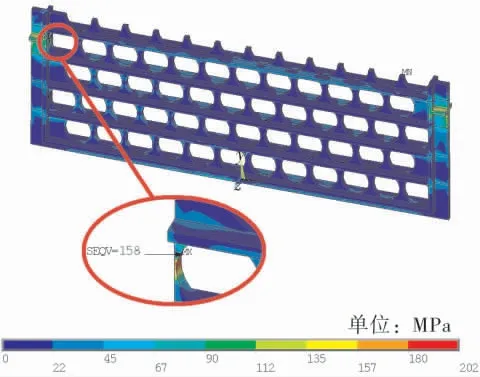
图6 直板形对流段中间管板等效应力
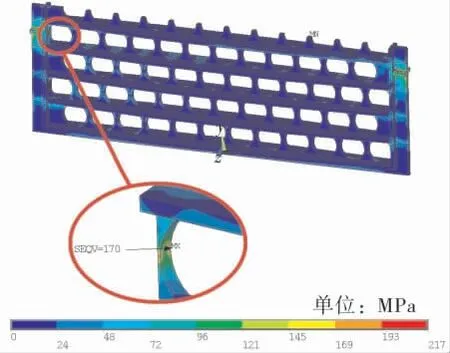
图7 直板加筋肋形对流段中间管板等效应力
对比图4可以看出, 波浪形对流段中间管板的应力分布与直板形和直板加筋肋形有一定差别,这主要是由于波浪形管板的筋板结构为波浪形,与直板形和直板加筋肋形管板相比,其每一排管孔处相互交错下沉,受力效果与前二者管板的不同。 从管孔局部应力分布来看,由于3种管板结构吊耳支撑处相同,因此导致开孔最大应力均出现在靠近吊耳处且应力分布相同。
3种管板结构的整体变形和危险路径处的应力计算结果见表2。 由表2中所列的整体变形数据可以看出,3种管板的变形量均为正值,其中直板形管板与直板加筋肋形管板的整体最大变形量相同,波浪形管板的小0.8mm,主要原因是直板形和直板加筋肋形管板的结构尺寸相同,而波浪形管板由于筋板形式为波浪形,上下排管孔孔心间的距离变小,使波浪形管板的整体高度低、质量变轻,整体变形就小;从表2所列的等效应力可以看出,3种管板结构中波浪形管板的等效应力最小(183MPa),与直板形和直板加筋肋形管板的等效应力相比分别降低9.0%和15.6%, 主要原因是波浪形管板结构的整体高度最低、 质量最轻,故等效应力最小,而直板形和直板加筋肋形管板结构的高度虽然相同,但加筋肋形管板的筋板宽度变大、质量最大、等效应力最大,直板形管板的质量次之、等效应力次之。
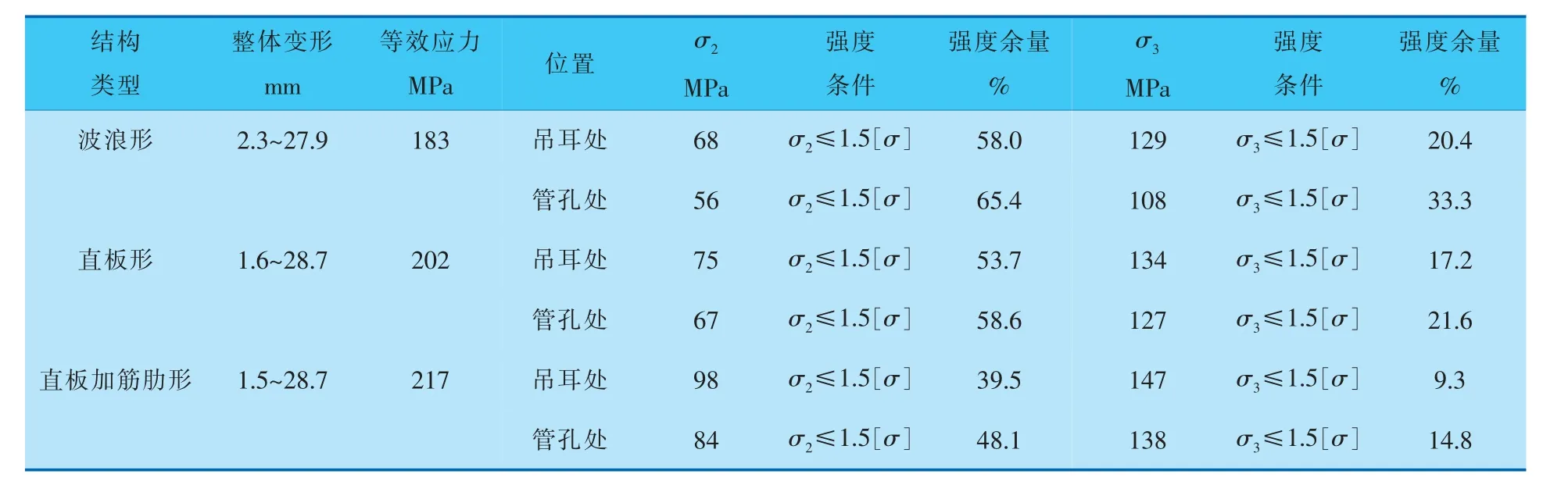
表2 不同结构管板整体变形和危险路径处的应力计算结果
由表2可知,3种管板中波浪形在吊耳处的σ2和σ3最小,主要是因为波浪形管板的质量最小,产生的薄膜应力和弯曲应力最小; 管孔处的σ2和σ3也最小, 主要是因为选取的3种管板管孔局部位置在吊耳附近,受管板吊耳处应力的影响,吊耳处应力越小,管孔处的应力也会越小。 对比3种管板的强度余量可以看出,波浪形管板在吊耳处和管孔处的σ2和σ3强度余量最大。
综上,波浪形对流段中间管板的等效应力在3种管板中最小, 并且波浪形管板的强度余量最大,所以波浪形管板有很大的优化空间,在强度安全的范围内,选择波浪形对流段中间管板进行优化。
4 波浪形对流段中间管板的优化设计
4.1 优化设计方法
理论上, 增加管板的厚度相当于加强其刚度,是降低应力的一个措施[16]。 但对流段中间管板进行优化设计时, 往往考虑将管板的厚度减薄,以满足轻质的要求,同时又由于管板的厚度决定其刚度。 因此,管板优化的过程中,需要在管板厚度与强度之间选择,通过有限元分析来获取一个合适的管板厚度。 在满足安全性的前提下,使管板质量减小,达到经济性的目的,以管板质量W为目标函数,管板厚度t为设计变量,管板的σ2和σ3为状态变量,对管板进行结构优化,优化设计的函数表达式为:
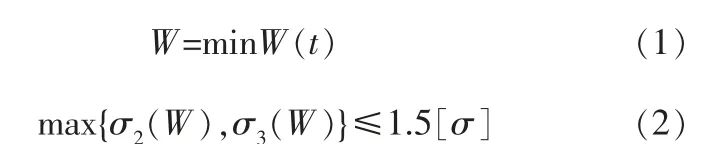
4.2 优化设计分析
不同管板厚度下,管板的变形、应力和各危险路径的应力评定见表3。
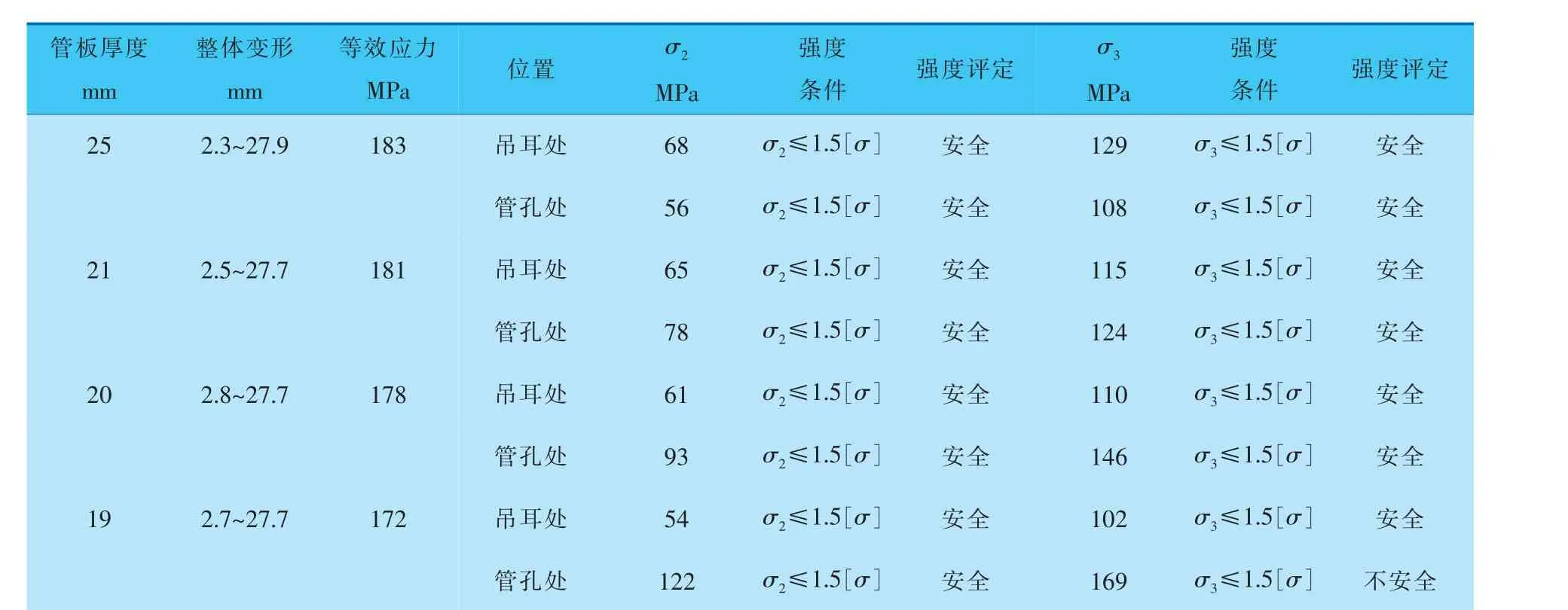
表3 不同管板厚度下的整体变形和危险路径处的应力计算结果
从表3中整体变形数据可以看出, 波浪形对流段中间管板厚度从25mm减薄到19mm时, 管板的变形量均为正值且逐渐减小,随之等效应力也不断减小,主要原因是管板厚度在减薄的同时质量也在减轻,管板吊耳处受到的支撑载荷不断减小。 对于管板吊耳处而言,由于管板吊耳处的σ2和σ3是通过管板等效应力最大点制定危险路径得出,因此与管板等效应力的下降趋势一致。 而管孔处的σ2和σ3不断增大, 根据σ2和σ3产生的原因可知, 当管板的质量随厚度减薄而减轻时,由于管板厚度对应力所起的作用更大,导致管孔处应力不断变大,所以当管板厚度减薄到19mm时,管孔处的σ3增加到169MPa,超出了管板的安全强度(162MPa),则优化后的管板厚度确定为20mm。
通过优化后,波浪形对流段中间管板厚度由25mm减薄到20mm, 质量由原来的517.1kg降为413.6kg,减轻了20%。
5 结论
5.1 考虑对流段中间管板复杂的结构形式,采用实体单元分别建立了直板形、波浪形和直板加筋肋形的三维有限元模型,该数值计算模型未经简化和等效,能够准确描述管板吊耳处和开孔处的受力特征,确保了管板数值计算结果的准确性。
5.2 依 据SH/T 3036—2012 和JB 4732—1995(2005年确认)要求进行管板强度评定。 通过充分对比3种管板的变形和应力计算结果, 发现波浪形管板的变形和等效应力在三者中最小,并且强度余量最大,故在保证管板强度的前提下,优先选用波浪形管板结构。
5.3 以管板质量W为目标函数, 以管板厚度t为设计变量,以管板应力σ2和σ3为状态变量,进行波浪形对流段中间管板的结构优化设计。 使管板厚度由25mm减薄到20mm,质量由原来的517.1kg降低为413.6kg,减轻了20%,达到了管板优化的目的,对高强轻质管板的设计具有重要意义。

