圆盘错流过滤黑液截留木质素数值模拟研究
杜钟雨 吴俊飞 赵文捷
(青岛科技大学机电工程学院)
木质素作为一种大量存在的可再生资源,具有巨大的应用潜力,工业木质素主要来源于制浆造纸工业和木材水解工业[1],通过过滤机过滤制浆黑液得到。 传统的过滤机理是滤液垂直于过滤介质的表面流动,固体被过滤介质截流,小颗粒通过过滤介质,大颗粒则被留在膜上达到过滤效果。 但是,随着过滤的进行,滤膜上会有固体物质堆积形成“滤饼”,且随着“滤饼”厚度逐渐增加,过滤速度会急剧降低,在过滤时需要进行人工排渣。 所以传统过滤必须使用絮凝剂或助滤剂[2]。
动态错流过滤是一种全新的过滤系统,原料液在压力泵的作用下, 通过进口进入滤室中,并一级一级地往下过滤。 由于滤膜的过滤作用,滤液通过滤膜时大颗粒被截留在滤膜上。 另外,在滤室中设置了连续转动的转子,使原料液产生旋流。 随着过滤的进行,原料液逐渐变浓,在过滤机的最末端,物料的浓度达到最高,这时就需要进行人工卸料。 动态错流过滤机广泛用于悬浮物的连续过滤和浓缩,过滤压力通常为0.4~0.6MPa;固体浓度可高达80%以上[3]。 通过研究,相对于传统的交叉流过滤,旋转圆盘过滤能产生更高的渗透通量和更好的溶质传输,因为它们在膜上产生的高剪切速率可以防止或限制“滤饼”的形成,而且高剪切速率和跨模压(TMP)的结合促进了大分子在膜上的传输[4]。
动态过滤机作为一种新型的过滤设备,自问世以来,受到国内外学者的广泛关注,并对过滤机的设备和过滤理论方面进行大量的实验和模拟研究。
日本学者Shirato于1986年首先研究了没有过滤过程、没有流体流入条件下,层流状态时的流体切向速度;1991年Yamaznki等在Shirato研究的基础上又对相同条件下湍流状态时流体切向速度的表达式进行了研究,且对牛顿型流体和非牛顿型流体进行了对比研究[5]。然而在实际操作中,旋转压滤机是有过滤过程和有滤液流入的,所以日本学者的研究与实际操作状态不符。
文献[6]中研究了层流状态(雷诺数Re<104)滤室内的流体过滤机理与流体的流速、剪应力和过滤速率的关系,在理论上进行初步讨论,但是只停留在有单面过滤、有流量的情况下。 天津大学课题组通过分析滤室内流体的流动机理,建立了数学模型并得到了实验验证,形成了一套滤室内流体流速的理论计算方法。
1996年,谭蔚等通过探针和激光多普勒测速系统测定了在不同条件下的切向速度并分析得出几个结论:滤室进口处的流量大小对进口两侧流体切向速度的影响呈相反趋势;流体的切向速度随着圆盘转速的增加而增加;通过分析给出了低浓度物料过滤面上的平均过滤速率表达式[7]。
近年来,如何提高压滤机的效率、减少功耗成了该领域的热点问题。 压滤机的过滤效率取决于滤室内的流场分布,而流场分布则直接受到圆盘转子高速运转形成的力场的影响,这与圆盘转子的转速及其与膜之间的间隔有着十分密切的关系。笔者将利用CFD软件Fluent对不同转速的圆盘转子压滤机滤室内部的流场进行模拟,可以避免实验条件和各种因素的限制, 得到特定转速、跨膜压作用下剪切速度和转子动压力的有效数据,为以后的研究积累经验。
1 滤室内部流体流动控制方程
滤室内部流体的流动要受到物理守恒定律的支配, 基本的守恒定律包括质量守恒定律、动量守恒定律和能量守恒定律。 对于本课题中的不可压缩流体,整个过程热交换可以忽略,所以能量守恒定律可以不考虑,只考虑质量守恒定律和动量守恒定律。
任何流动问题都要遵循质量守恒定律,可以表述为: 单位时间内流体微元体中质量的增加,等于同一时间间隔内流入该微元体的净质量。 因此可以得到质量守恒方程为:
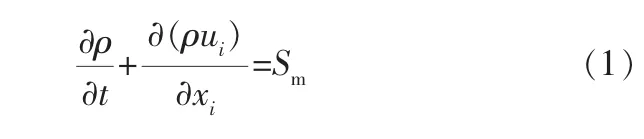
该方程同时适用于可压缩流动和不可压缩流动。 Sm是从分散的二级相中加入到连续相的质量,当然也可以是任何自定义源相。
任何流动系统都要遵守动量守恒定律,可以表述为:微元体中流体的动量对时间的变化率等于外界作用在该微元体上的各种力之和。 因此可以得到动量守恒方程为:

2 计算模型的建立
2.1 几何模型的建立
如图1所示, 使用NX-UG完成一级滤室的三维模型建立。In和Out分别表示黑液进口和滤液出口。 其中圆盘转子与膜的距离C=15mm,圆盘的直径D=128mm,滤室的直径T=137mm,滤室的厚度H=30mm。 滤室模型正等轴测图如图2所示。
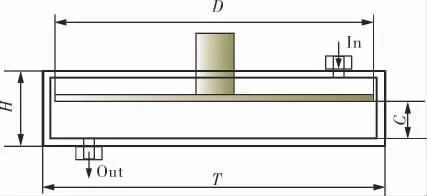
图1 一级滤室几何模型尺寸标注

图2 滤室模型正等轴测图
2.2 数值模型的建立
在NX-UG中创建滤室和旋转圆盘的三维模型,考虑到Fluent中选用MRF(多重参考系)模型进行计算, 所以对整个模型进行动静区域划分,此步骤直接在UG中使用求“减”运算来完成。在整个滤室内建立一个圆柱块体将整个圆盘包住作为动区域,整个滤室内充满黑液作为静区域。 这个圆柱块体的外表面设置成一对相对应的Interface,作为能量传输界面,使得动区域转子产生的旋流能够影响到静区域。 另外,在滤室的出口附近建立一个多孔介质区域,同理,多孔介质区域外边界也为一对Interface作为能量的传输界面。因为圆盘内部不参与流场计算且不考虑传热等,所以直接求“减”运算且不保留工具体,圆盘只保留一个外壳形状的面,后续边界条件设置直接将之设置为Wall。 然后再次对圆柱体、 多孔介质区域和整个滤室腔做“减”运算,并保留工具体,目的是为了在动区域和静区域中都有一个可以选择的面定义为一对Interface。
完成三维模型的建立之后将之另存为Parasolid(.x_t)格式的文件并导入Workbench Mesh进行网格划分, 将导入模型的3个body重命名为liquid、swirl-area、membrane, 分别代表黑液区、动区域和膜。 划分的网格数为651 023,质量检测良好,平均质量为0.81。整体网格划分如图3所示;具体的分区如图4所示; 圆盘和滤膜区域进行了网格加密(图5)。

图3 整体网格划分

图4 边界类型及分区示意图

图5 圆盘及滤膜区域网格划分
2.3 边界条件设置
使用Fluent对滤室内部的流场进行模拟,基于常用的压力与速度耦合的SIMPLE算法,SIMPLE算法的核心思想可以概括为:给定压力场,求解离散形式的动量方程,从而得到速度场,与本模拟相吻合。模型选用RNG k-ε模型,该模型计算速度梯度较大的流场时精度更高,且考虑到旋流效应,对旋转流动计算精度有所提高,因此更加适用于本旋流模型。 材料物性设置中,黑液的密度设置为1 098kg/m3,粘度为5.85mPa·s。边界条件设置中, 入口类型为进口压力, 分别为0.5、1.0、1.5、2.0bar(1bar=0.1MPa)。 出口类型为压力出口,压力为零。
旋转圆盘设置为Wall边界条件, 分别以300、800r/min的速度旋转, 旋转类型设置为Moving Wall,且与邻近单元相对转速为零,实现与周围流体同步运动,不存在相对运动。
旋转流体区Swirling-Area: 在运动类型中选择多重参考系MRF模型,运动方式为转动,旋转速度分别为300、800r/min。 旋转方向为绕z轴正方向。
Liquid区域同样选择MRF模型, 运动方式相对于动区域运动,旋转方向为z轴正方向。
2.4 多孔介质区域设置
因为流场中存在滤膜,设置边界时就需要使用多孔介质条件,以提高计算精度。 多孔介质模型的动量方程就是在标准动量方程的基础上加了源项Si, 这个源项包括粘性损失项和惯性损失项,即:

2.5 假设条件
在整个滤室内部,湍流流场很复杂,需要对其中几个条件进行假定:黑液在滤室内部做定常且不可压缩流动,且整个过程为恒温过程;文中的研究对象是压滤机的一级滤室,所以混合物浓度相对较低,可以忽略液固相之间的相互作用力。
3 模拟结果及讨论
由Fluent通过后处理可以得到圆盘转子动压力云图和膜表面的速度矢量图,结论中主要观察了圆盘转子的转动引起的膜剪切速度的变化和转子动压力的变化。
3.1 圆盘转子动压力的变化
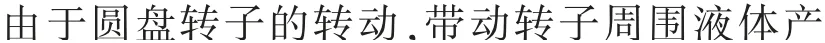

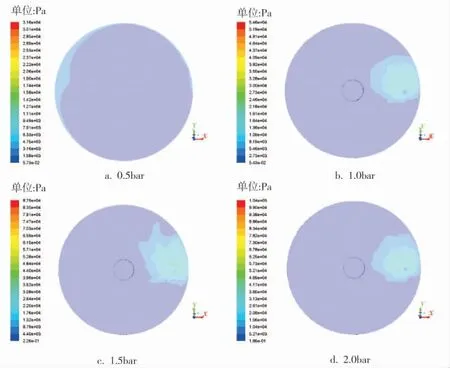
图6 转速为300r/min时圆盘转子的动压云图
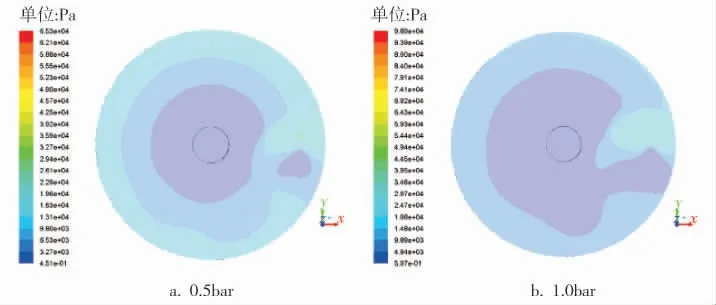
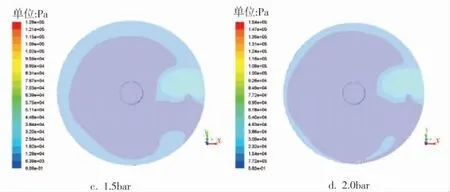
图7 转速为800r/min时圆盘转子的动压云图
根据动压变化散点图(图8)可知,当转速为300r/min时,此时的动压最大为949Pa(0.5bar条件下),最小为606Pa(1.5bar条件下);当转速增大为800r/min时,动压数值随进口压力的增大而增大。0.5bar 时 动 压 达 到 了6 162Pa,2.0bar 时 最 大 为7 643Pa。计算得知,相同进口压力条件下,800r/min时要比300r/min时的动压力高很多, 最高相差12倍。 另外,根据图8可以很清晰地发现,300r/min、0.5bar时的动压为4个压强下最大; 而800r/min、2.0bar时的动压为4个压强下最大。
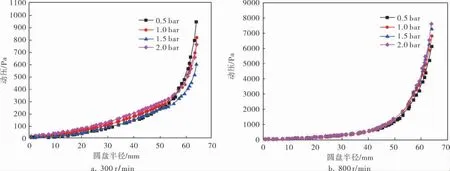
图8 不同压力下动压变化散点图
3.2 膜附近流场剪切速度的变化
膜附近流场的变化,直接受到圆盘转速的影响。 另外,Interface界面的定义也保障了动区域、静区域和膜区域之间的能量传输,保证圆盘旋转产生的力场直接影响到膜附近的流场。 通过Fluent后处理可以得到流场的剪切速度矢量图,笔者截取了距离滤膜最近的z=2mm的等值面作为目标面,查看流场的剪切速度变化。
由两个速度矢量图(图9、10)可以看出,剪切速度沿膜半径的增大而增大, 由图9、10可以得知,当圆盘转速为300r/min时,目标面的剪切速度最大达到1.29m/s, 而当转速增大到800r/min时,4个进口压力下最大剪切速度达到3.70m/s。 同样进口压力作用下剪切速度是300r/min时的2.8倍左右。 另外,由两个散点图(图11)不难看出,转速较低时,剪切速度随着进口压力的增大而呈现逐渐减小的趋势,且进口压力的变化对于剪切速度的影响相对较明显;转速较高时,剪切速度随着进口压力的增大而增大,进口压力的变化对剪切速度的影响较小。
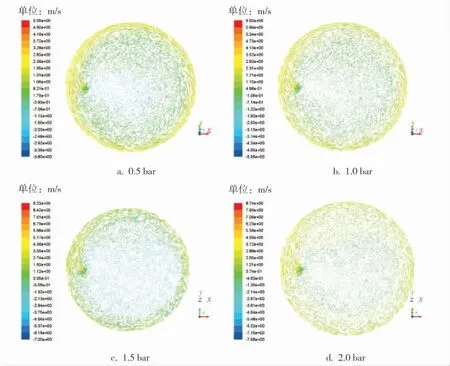
图9 转速为300r/min时膜上剪切速度矢量图
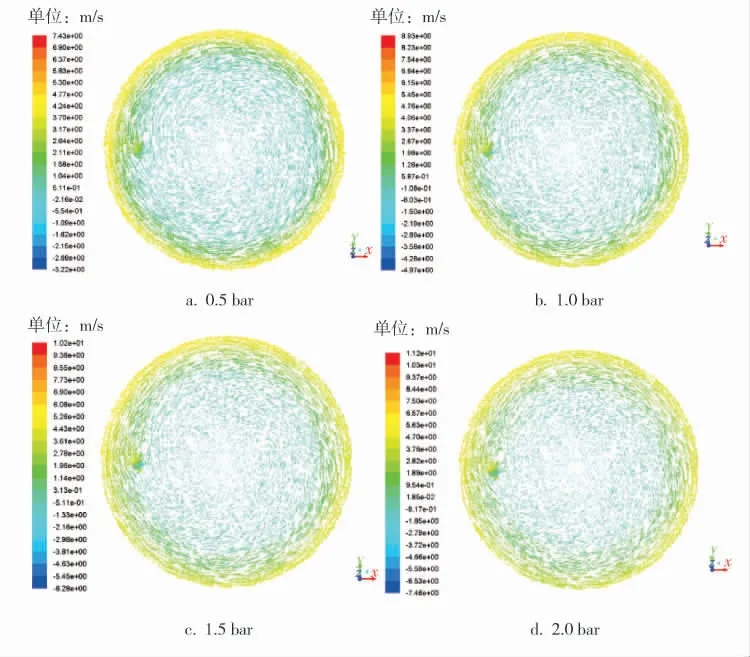
图10 转速为800r/min时膜上剪切速度矢量图

图11 不同压力下剪切速度变化散点图
4 结论
4.1 用Fluent软件对圆盘错流过滤机的一级滤室进行流场模拟,分别模拟了圆盘转速为300r/min和800r/min时不同跨膜压作用下的流场情况,当圆盘转速为300r/min时, 圆盘动压力在1.5bar时进口压力下最小,为600Pa,在0.5bar时最大,为949Pa;而当转速为800r/min时,随着进口压力设置参数逐渐增大而增大。 相同进口压力条件下,800r/min时要比300r/min时的动压力高很多,最高相差12倍。
4.2 当圆盘转速为300r/min时,4种进口压力条件下剪切速度最大值的下降趋势为0.5bar>1.0bar>1.5bar>2.0bar,最大达到1.29m/s;当转速为800r/min时,4种进口压力条件下剪切速度最大值的下降趋势为2.0bar>1.5bar>1.0bar>0.5bar, 最大达到3.70m/s;转速较低时,进口压力的变化对于剪切速度的影响相对较明显。

