服役构件疲劳损伤的声发射信号特征提取
冷建成 王玉洁 钱万东 刘 晔
(东北石油大学机械科学与工程学院)
管道、压力容器等化工设备在工业、民用及军工等许多领域都有着重要的地位和作用,尤其在石油、 化工行业应用极为广泛。 TSG R0004—2009《固定式压力容器安全技术监察规程》中规定,压力容器设计时必须标明设计使用年限或循环次数,即一般情况下,到达设计使用年限的压力容器应当报废;然而为了规避风险,有些设备设计使用年限往往较短,因此,设备达到设计使用年限并不意味着没有继续使用的可能性。
再制造工程就是一种通过修复或改造报废产品而延长其剩余使用寿命的新兴产业,而无损检测和寿命预测技术对再制造毛坯的可再制造性评价和再制造产品是否符合生产使用标准起到了关键性作用。 由于声发射检测可以实时跟踪再制造构件在疲劳损伤过程中的变化趋势,因此相比其他离线检测方法更加适用于剩余寿命的预测。Miura S等在研究铝合金的声发射疲劳试验中,发现累积计数值可以将整个疲劳过程分为类似于疲劳循环的3个阶段[1];柴孟瑜等通过研究Q345R钢在疲劳裂纹扩展过程中声发射累积计数值和累积能量值的变化,建立了声发射计数率和能量率与疲劳裂纹扩展速率之间的关系[2]。 Yu J等研究了声发射累积绝对能量、累积计数和疲劳裂纹扩展尺寸与载荷循环次数之间的关系[3];Miguel J M等利用声发射技术对不同变形程度的试样进行研究,通过声发射计数率的变化规律建立了声发射事件的数量和振幅与裂纹类型之间的关系[4]。 Megid W A等则通过实例研究并证实了利用声发射技术监测钢桥吊环疲劳裂纹萌生和扩展的有效性[5]。 为进一步深化认识金属疲劳过程中的声发射信号特征,黄振峰等引入混沌特征中的K熵和关联维数来探索声发射信号与疲劳损伤程度之间的关系[6]。在再制造无损检测领域,Shi Y等构建了以声发射能量、计数参数动态表征曲轴疲劳裂纹扩展深度与机器视觉表征疲劳裂纹表面长度的双参量曲轴剩余寿命预测模型[7,8]。
可见,声发射在再制造检测方面的应用相对较少,同时由于声发射信号容易受到外部噪声的干扰,笔者的目的就是在声发射基本参数的基础上,提出一种基于小波包能量谱和小波熵的声发射特征参数提取方法,进而表征不同疲劳阶段的损伤累积程度, 为后续的寿命评估提供参数依据。
1 疲劳试验
1.1 试件
试件材料为Q235B碳素钢, 其屈服强度为235MPa,抗拉强度为375~460MPa,因其塑性、强度及焊接等性能得到较好配合且成本相对低廉而广泛应用于现代工程领域。 试验采用中间带有预制V形缺口的试件, 以便于合理布置声发射传感器跟踪监测疲劳裂纹发展过程,试件具体尺寸如图1所示。
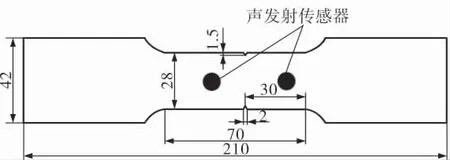
图1 V形缺口板状试件的形状和尺寸
1.2 试验设备
试验设备主要包括加载设备和声发射在线监测系统, 其中加载设备采用QBG-300微机控制高频疲劳试验机,该试验机为微机控制,最大静负荷为±300kN,动负荷为180kN,循环次数值精确到0.1千次,其工作原理是基于电磁谐振,由试件连同夹具与试验机组成的系统在电磁铁激励下产生共振,以此来对试件施加循环载荷。
声发射在线监测系统主要由传感器、前置放大器、采集器和信号记录与分析软件组成,如图2所示, 其中传感器选用WSα型宽频带传感器,其频率范围为100~1 000kHz, 谐振频率为125kHz;前置放大器选用40dB的增益型放大器;采集器为PCI-2声发射系统, 配套采用AEwin采集分析软件。
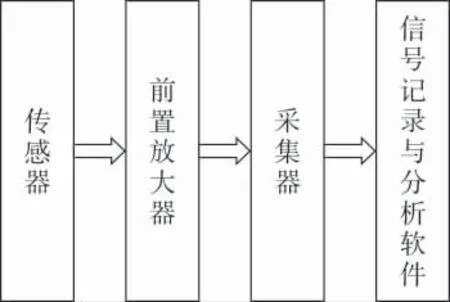
图2 声发射在线监测系统组成
1.3 试验方法
首先将试件夹持在高频疲劳试验机上、下夹具之间,然后在声发射传感器陶瓷面上涂上耦合剂真空脂与试件进行耦合, 在预制V形缺口两侧对称布置2个传感器(图1),并用胶带固定,现场照片如图3所示。

图3 声发射监测试验设备现场照片
为减少试验过程中的背景噪声干扰,前置放大器增益设置为40dB, 声发射门槛值设置为40dB,采样频率设置为1MHz。 基于GB/T 3075—2008《金属材料 疲劳试验 轴向力控制方法》,在疲劳试验机控制程序中, 分别输入静载荷12.6kN和动载荷5.4kN,同时同步开启声发射监测设备, 自动记录2个监测点在整个疲劳循环过程中的声发射信号变化,直至试件断裂。
2 试验结果分析
分别对1#~4#试件进行了疲劳试验,结果表明声发射信号具有相似的变化规律, 为此仅以3#试件为例进行分析。
2.1 不同循环次数下的声发射信号
常用的声发射参数有幅值、能量、计数、上升时间及持续时间等, 图4给出了声发射信号在疲劳循环初始阶段的幅值变化曲线。
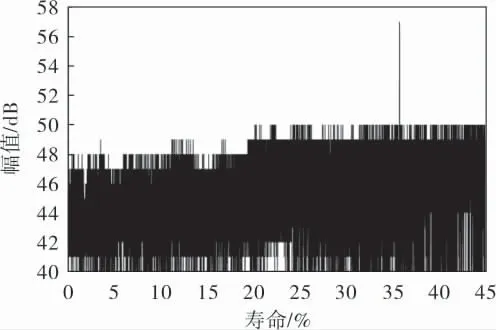
图4 初始阶段的声发射信号幅值
由图4可见, 幅值分布相对均匀, 且相对较小,基本都稳定在50dB左右;这个阶段的声发射波形呈良好的周期性, 电压幅值较小, 稳定于10mV左右,如图5所示。
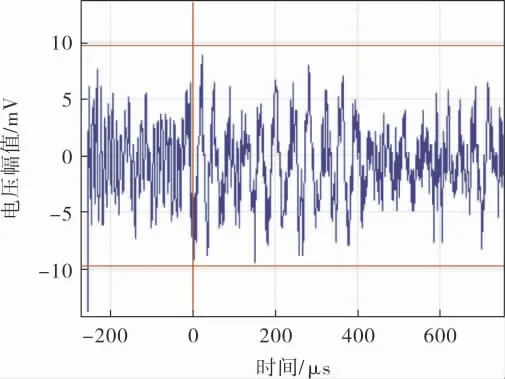
图5 初始阶段的声发射信号波形
随后经过长时间的疲劳循环,在中间阶段声发射信号幅值呈现出一定程度的不稳定跳动,跳动幅度一般在55~65dB之间,如图6所示。
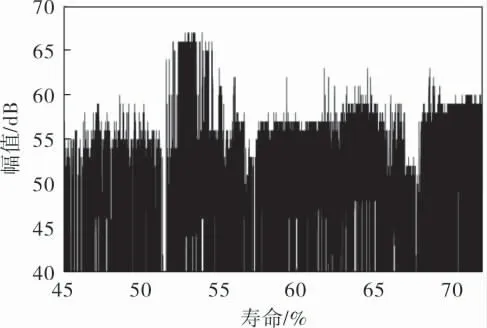
图6 中间阶段的声发射信号幅值
由图6可知,该阶段出现突发型声发射事件,声发射信号向高频区转移,而波形信号开始出现不同程度的波动,如图7所示。
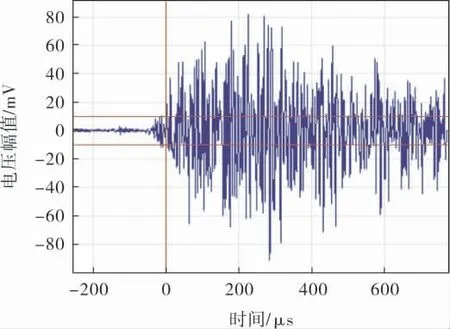
图7 中间阶段的声发射信号波形
由图7不难发现,相对于循环初始阶段,中间阶段的声发射波形电压幅值明显增大,最大电压达到80mV。 通过微观机理分析,这主要是由于试样内部缺陷的增值与位错滑移过程中会产生较大程度的应力波,随之被声发射探头所采集,因而引起声发射信号的改变[1]。
随着疲劳循环周次的增加,裂纹由稳定扩展逐步发展为失稳扩展,随后试件迅速断裂,此时的声发射信号幅值会达到峰值,如图8所示。

图8 后期阶段的声发射信号幅值
相对应的,声发射波形多以高衰减特性的突发型信号为主,如图9所示,这主要是由于试件裂纹大面积开裂瞬间释放大量的能量,进而形成强度较大的声发射信号, 该信号突变幅值高达300mV, 但信号衰减较快, 衰减时间仅为300~400μs。
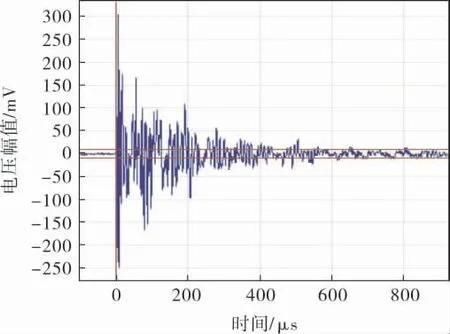
图9 后期阶段的声发射信号波形
在实际测试时, 由于现场有很多噪声干扰,单纯利用幅值、波形等声发射信号基本特征很难准确反映疲劳损伤的发展过程,为此提出基于小波包能量谱和小波熵的损伤特征提取方法。
2.2 小波包能量谱分析
小波变换只对信号的低频部分做进一步分解, 而小波包变换既可以对低频部分进行分解,也可以对高频部分进行分解,而且这种分解既无冗余也无疏漏,所以对包含大量中、高频信息的信号能够进行更好的时频局部化分析。 由于需要对高频能量进行详细分析,因此笔者选用小波包变换对声发射信号进行处理。

其中,g(k)=(-1)kh(1-k),即2个系数也具有正交关系。在多分辨分析中,退化尺度函数φ(t)和小波基函数ψ(t)满足如下双尺度方程:

由于φ(t)由hk唯一确定,因此又称{Un(t)}n∈Z为关于序列{hk}的正交小波包。
若设{Un(t)}n∈Z是φ(t)的正交小波包,则有(Un(t-k),Un(t-l))=δu,即{Un(t)}n∈Z构成L2(R)的规范正交基。
小波包分解的层数与信号的分析精度关系紧密,若分解的层数越少,则分析速度越快,但同时频带分辨率就相应减小; 若分解的层数越多,则频带分辨率也越高。 设采样频率为p,则经过n层小波包分解得到的频带的分辨率为p/2n。 以3层小波包分解为例,其分解树如图10所示。
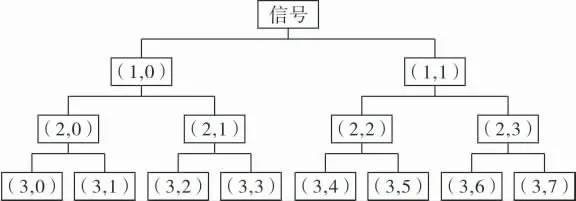
图10 3层小波包分解树
利用dB4小波包分解对疲劳试验过程中初始阶段、中间阶段和后期阶段的声发射波形信号分别进行3层小波分解与重构, 其中第3层8个节点(0~7)的 频 率 范 围 分 别 为0~8Hz、8~16Hz、16~24Hz、24~32Hz、32~40Hz、40~48Hz、48~56Hz 和56~64Hz。
在循环初始阶段,声发射波形频率主要集中在40Hz以下,高频能量占比较小,是典型的低频连续型声发射信号,如图11所示。
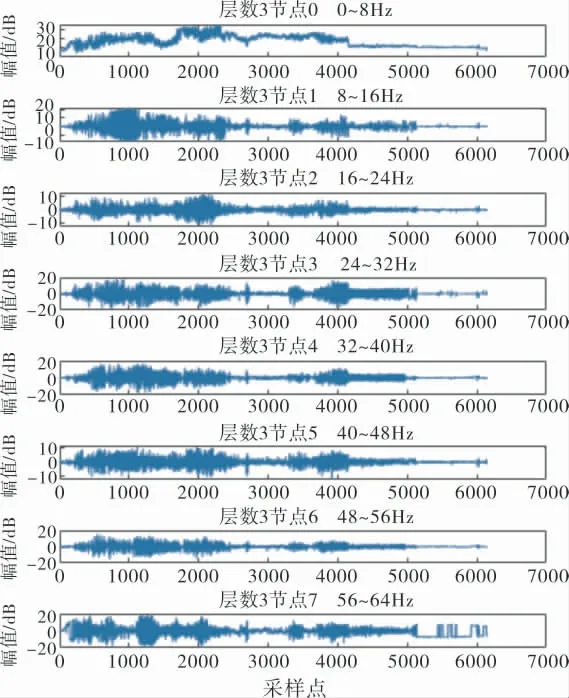
图11 初始阶段小波分解频率分布
试件进入疲劳中间阶段时,小波分解结果如图12所示。
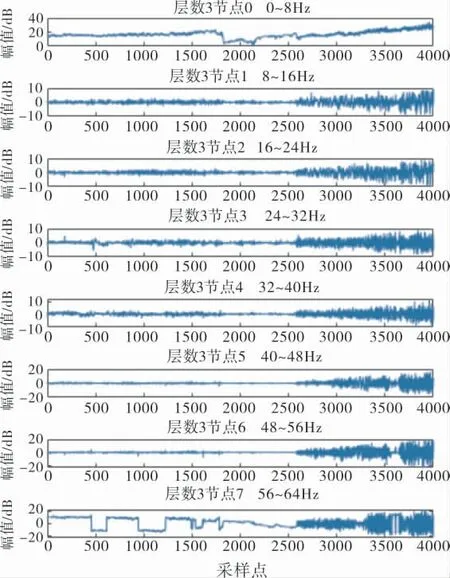
图12 中间阶段小波分解频率分布
由图12不难发现,各个频率段的能量占比分布均匀,但电压值极不稳定,与之前声发射幅值的变化趋势相似, 每个频率段信号都有较大波动。
试件在疲劳后期阶段,信号逐渐向高频段转移,高频信号能量占比增大,且电压信号逐渐衰减,如图13所示。
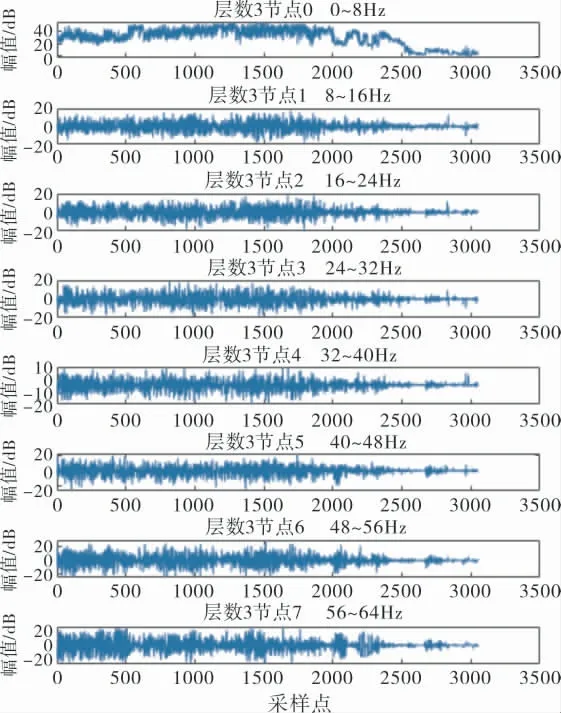
图13 后期阶段小波分解频率分布
为了更加直观地反映声发射信号随着疲劳循环的变化趋势,将疲劳寿命均匀划分为10个阶段,对每个阶段分别进行小波分解与重构,最后计算得到各阶段的高频能量占比,即设各阶段总能量为E, 频率在56~64Hz范围内的能量为Eh,则高频能量占比t=Eh/E, 画出各阶段的高频能量占比如图14所示。
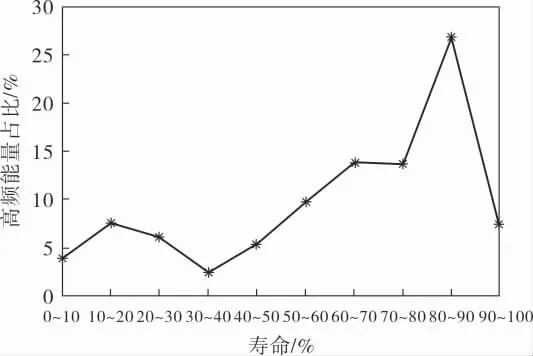
图14 不同寿命阶段的高频能量占比
由图14可知,试件在疲劳初始阶段,即对应着裂纹萌生阶段,声发射信号的能量主要分布在低频段范围内,所以高频能量占比较低,大约在5%左右;随着循环的进行,裂纹进入稳定扩展,声发射信号能量开始向中间频段转移,所以高频能量占比逐渐增大;到疲劳后期时,裂纹进入失稳扩展, 声发射信号能量越来越多地转移到高频段, 高频能量占比上升到28%, 最后试件突然断裂,高频能量占比急速下降。
2.3 小波熵特征提取
小波熵由小波变换和信息熵构成,首先通过小波变换进行多尺度多分辨率分析,将所得的各尺度小波系数处理成概率分布序列;然后由这个序列计算得到熵值,即表征这个系数矩阵的稀疏程度, 它反映了整个信号的不确定性和复杂程度。
定义某一尺度下小波分量的能量为该尺度下小波系数的平方和:

其中,E1,E2,…,En为不同小波尺度的能量,按小波函数的尺度自然划分。
由正交小波变换的特性可知,各尺度分量的能量之和就是信号总能量:

将各尺度分量的能量归一化处理,得到原始信号能量在不同小波尺度下的分布为:

由此定义小波熵为:

利用dB4小波对声发射信号进行3层小波包分解,得到8个频带的信号序列;然后对重构后不同寿命区间的信号进行信息熵计算,得到声发射信号的小波熵变化趋势,如图15所示。
由图15可以看出,裂纹萌生阶段试件状态比较稳定,信号波动较小,因此小波熵比较小且比较稳定;随着循环次数的增加,在裂纹稳态扩展阶段,试件内部的能量愈发不稳定,小波熵逐渐增大;到了裂纹失稳扩展阶段,试件迅速断裂,信号波动由剧烈归于平静,因此小波熵迅速下降。
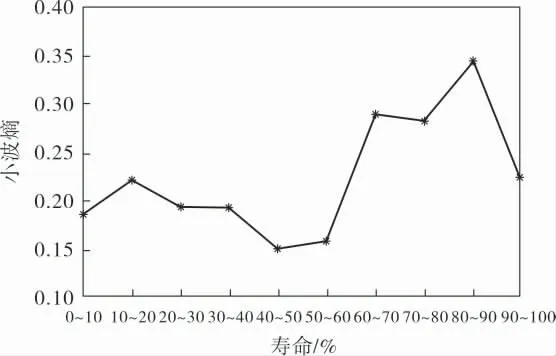
图15 不同寿命阶段的小波熵
3 分析与讨论
通过对声发射幅值、波形、高频能量占比和小波熵的分析对比不难发现:在疲劳循环的不同阶段,各特征参数表现出不同的变化规律,整体变化趋势见表1。
由表1可以看出,在初始疲劳阶段,声发射信号幅值较低,稳定在50dB左右;波形信号比较有规律,电压值最大只有10mV;高频能量占比只有5%左右, 稳定在较低水平; 小波熵大致在0.15~0.20之间,稳定在较小范围内。 在循环中期,声发射信号幅值增大,且一直在55~65dB范围内波动;波形多次出现不同程度的突变,对应的电压值明显增大,最高达到80mV;部分声发射信号向较高频段转移,各个频段分布均匀,高频能量占比逐渐上升到15%;小波熵增加较快。到了疲劳后期阶段,声发射信号幅值增大且均超过60dB,甚至很多在65dB以上;电压值突增至300mV;同时,越来越多的声发射信号向高频段转移,高频能量占比最终上升到28%;小波熵也迅速上升到0.35,至断裂时急剧下降。

表1 各阶段的声发射信号特征
基于疲劳损伤演化机理,可将试件的整个寿命划分为裂纹萌生、裂纹稳态扩展、裂纹失稳扩展及断裂等几个阶段,而所提取的声发射信号特征参数,尤其是高频能量占比和小波熵可以很好地反映疲劳损伤的累积发展过程,为后续建立声发射信号特征与寿命之间的映射关系提供参数依据。
4 结论
4.1 对Q235B钢试件进行了拉-拉疲劳过程中声发射信号的实时监测,结果表明声发射信号的幅值和波形电压在疲劳循环初始、中间和后期阶段的变化呈现出与裂纹萌生、裂纹稳态扩展和裂纹失稳扩展相对应的3个阶段。
4.2 通过对声发射监测数据进行小波包能量谱分析和小波分解与重构,分别得到各寿命阶段的声发射信号高频能量占比和小波熵,结果表明试件在裂纹萌生阶段的高频能量占比为5%左右,信号波动较小,而小波熵比较小且相对稳定;在裂纹稳态扩展阶段,声发射信号高频能量占比逐渐上升至15%,试件内部的能量愈发不稳定,而小波熵逐渐增大;在裂纹失稳扩展阶段,声发射信号高频能量占比上升速率变大,信号波动幅度逐渐减小,而小波熵迅速下降。
4.3 所提取的声发射信号高频能量占比和小波熵随着寿命的变化呈现出明显的3个阶段, 反映了不同疲劳阶段的损伤累积程度,可作为后续预测剩余寿命的特征参数。

