基于改进经验傅里叶分解的工作模态分析
周 伟,冯仲仁,王雄江
(武汉理工大学 土木工程与建筑学院,武汉 430070)
随着大跨桥梁和超高层建筑的兴建,近年来健康监测系统在此类大型土木结构中得到广泛应用。健康监测系统主要目的为对结构的状态进行实时监测和评估,实现损伤预警,而其基础为结构的模态参数识别。由于工作模态分析实用且成本低廉,越来越多的研究人员正在探索环境激励下的模态识别技术[1-5]。
自经验模态分解(empirical mode decomposition,EMD)被运用在模态识别中以来,各地学者致力于将各种非平稳信号分解方法运用至结构模态识别。Perez等利用同步挤压小波变换(synchrosqueezed wavelet transform,SST),结合随机减量技术、Hilbert变换(Hilbert transform,HT)及Kalman滤波,对环境激励下的四层benchmark框架和实桥进行模态识别[6]。Amezquita-Sanchez等[7]和Xin等[8]分别利用多重信号分类算法和标准自回归功率谱改进经验小波变换(empirical wavelet transform,EWT),并将改进EWT应用于结构的模态识别。Bagheri等[9]将变分模态分解(variational mode decomposition,VMD)应用于结构模态分析中,并使用实验框架和人行天桥检验该方法。上述各种信号分解算法尽管在模态识别中取得一定成绩,但也存在一些困难。例如,EMD没有数学理论基础,分解的信号分量存在端部效应和模态混淆;SST母小波无自适应性;EWT中滤波器的过渡带导致密集模态信号分解分量产生混淆;VMD同样不适用于含密集模态的信号。
近日,为了减轻上述困难,一种新的非平稳信号分解方法被提出,即经验傅里叶分解(empirical Fourier decomposition,EFD)[10]。该方法结合EWT和傅里叶分解法[11]的思想,具有自适应、数学理论完备和处理密集模态等特点,是一种有应用前景的信号分解方法。然而,与EWT相同,基于傅里叶频谱峰值进行频带分割是EFD的关键。对于低信噪比信号,频谱的毛刺极大地影响了频带分割的准确度,这使得EFD无法直接处理环境激励下结构的振动信号。基于此,本文提出自回归(auto regression,AR)功率谱对EFD改进,得到改进EFD(improved empirical Fourier decomposition,IEFD),并对四层模拟框架和某人行斜拉桥进行工作模态分析。此外,利用协方差驱动的随机子空间(covariance-driven stochastic subspace identification,SSI-cov)分析以对比结果。
1 经验傅里叶分解及改进
1.1 原始经验傅里叶分解
经验傅里叶分解(EFD)通过对原信号的傅里叶谱进行分割,再对每个分割区间进行逆向傅里叶变换,从原信号中提取出不同频率分量的信号。首先,将原信号傅里叶谱归一化到区间[0,π],假定划分成N个连续的区间,每个区间表示为Ω= [ωi,ωi+1]。确定分割区间后,定义解析傅里叶固有频带函数。
将x[n]设置为长度为K的离散时间序列信号,并将离散傅里叶变换应用于x[n]
(1)
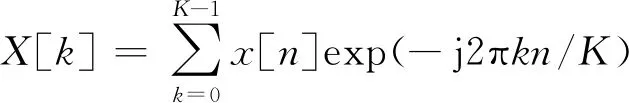
(2)
式中:Re{v[n]}表示v[n]的实部;v[n]和v*[n]是复共轭的。v[n]广义傅里叶级数展开为
(3)
式中:N表示频谱分割区数。最终,依据频谱分割区间[ωi,ωi+1],得解析傅里叶固有频带函数
(4)
1.2 改进经验傅里叶分解
当一个信号被显著的噪声或非平稳分量污染时,利用傅里叶频谱来分割区间是不理想的。针对此问题,本文提出利用AR模型的功率谱进行频带分割,以确定解析傅里叶固有频带函数的上下限。
假设存在平稳随机信号序列x(m)为一个AR(p)过程,则该序列有差分方程
(5)
式中,ω(m)是方差为σ2,均值为零的白噪声激励信号。AR模型的自相关函数可以用矩阵形式表示为
(6)
式中,rxx()为自相关函数。式(6)描述的线性方程称为Yule-Walker方程,系数ak和σ2可通过使用Levinson-Durbin递归算法求解。该随机过程的功率谱密度可表示为
(7)
确定AR功率谱之后,本文利用EFD中相同的方法确定分割边界,进行AR功率谱分割。首先,将AR功率谱归一化至区间[0,π],假定将功率谱划分为N个连续的区间,共需确定N+1个边界。其次,在功率谱中寻找M个控制点,即初值和极大值。其中,分段数N与控制点数M有如下关系
(1)当M≥N时,功率谱有多余的控制点来确定N个分段,固只保留按降序排列的前N个控制点。
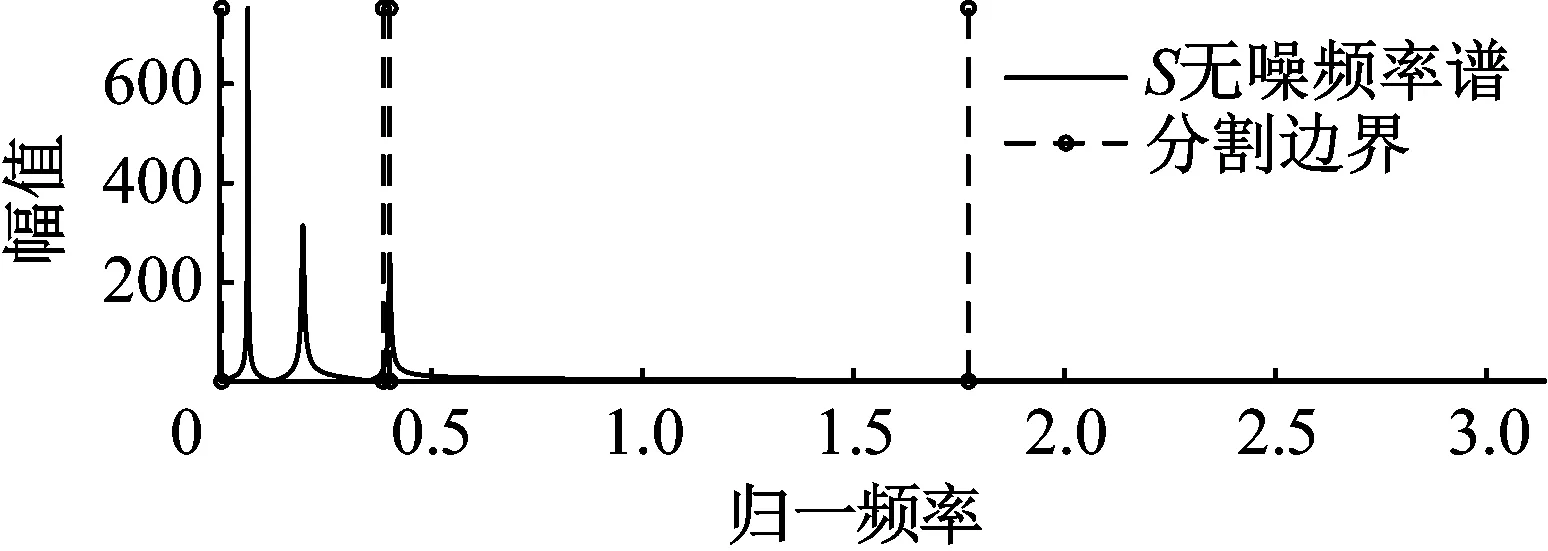
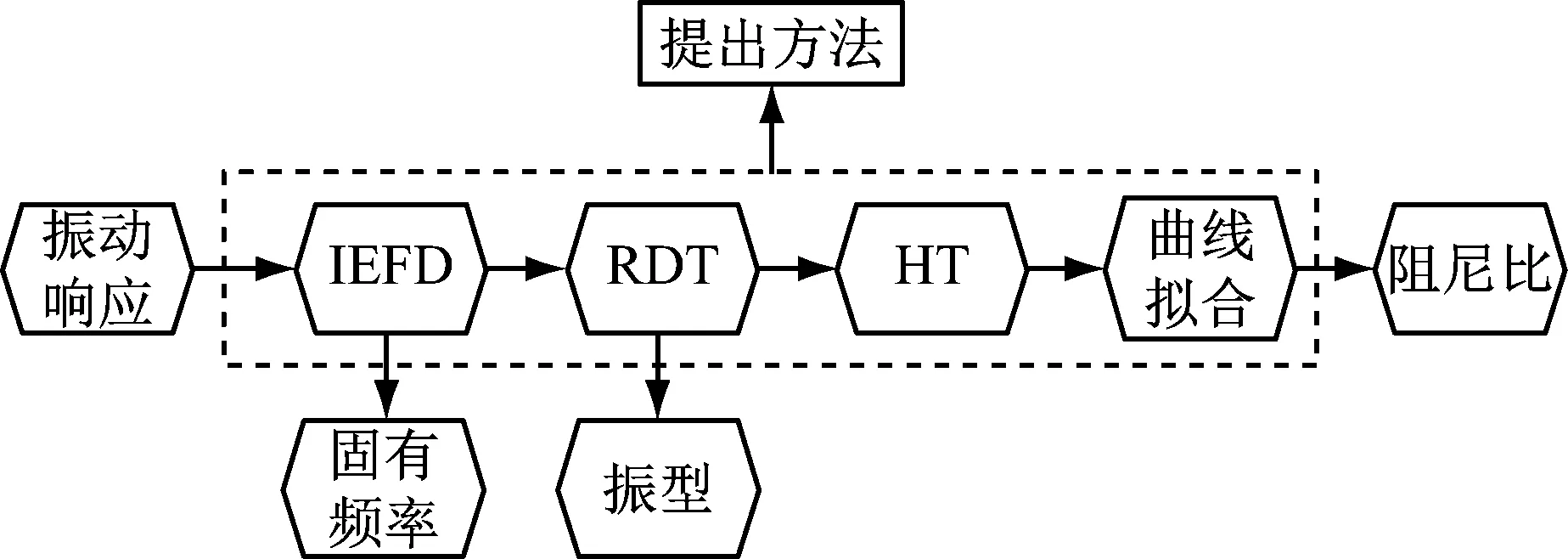
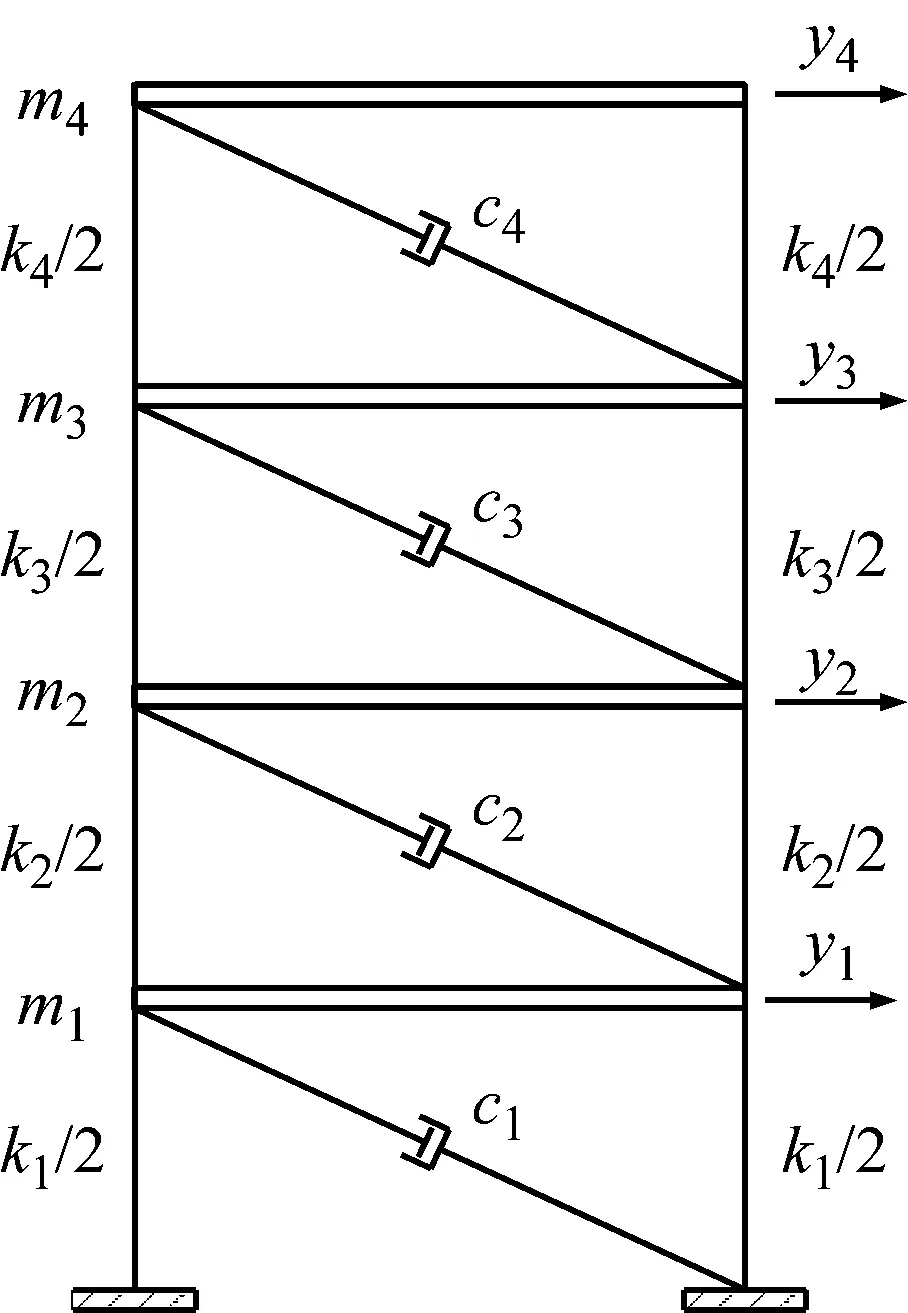
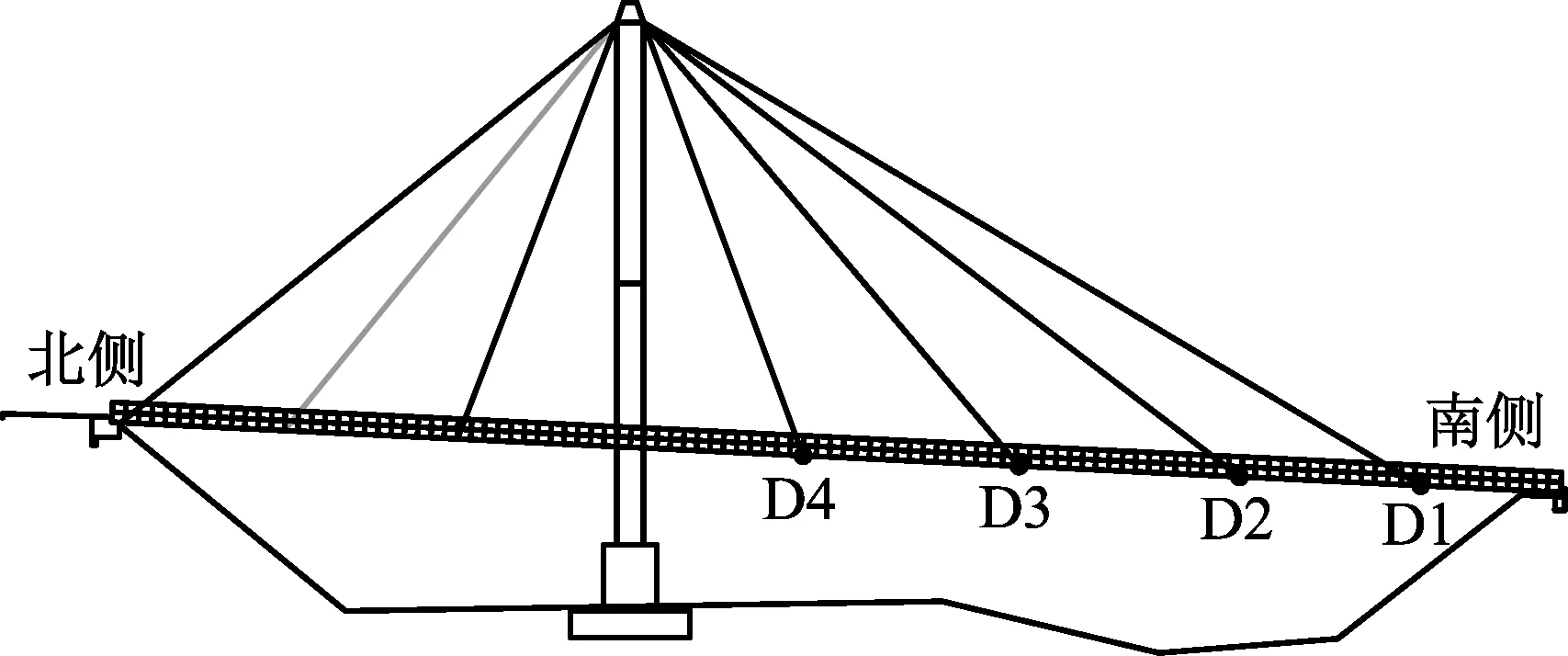
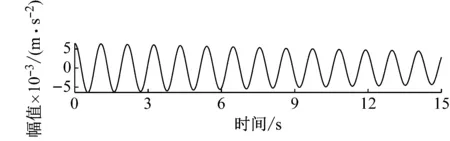
(2)当M 然后,记录控制点的位置ωn(其中1 ≤n≤N,ω0= 0,ωN+1=π)。前N个边界定义为区间[ωn-1,ωn]中功率谱最小值ωn,并将这些最小值的集合表示为Ωn,而第N+1个边界则由ωN和ωN+1的中点确定。AR功率谱分段边界可描述为 (8) 基于AR功率谱改进的EFD主要分为两个步骤,IEFD的框架如图1所示。由图1可知:第一步,计算处理信号的AR功率谱,确定分割边界;第二步,根据确定的分割边界,利用EFD将振动信号分解成若干分量。 图1 改进经验傅里叶分解流程图Fig.1 Flow chart of IEFD 为了对比IEFD和EFD在信号处理中的效果,对加噪的三自由度结构自由振动响应S进行分解。该模拟信号由式(9)给出。 (9) 式中:Ai为幅值;ζi为阻尼比;fi为频率;R(t)为高斯噪声;θi为第i阶频率的相位角。本例各参数如表1所示。 表1 含噪合成信号参数Tab.1 Parameters of the synthetic signal IEFD和EFD对含噪信号S处理的分割区结果如图2所示。其中,为了提高分割效果的辨识度,将含噪信号S去除噪声的频率谱和分割边界组成图2。由图2可知,IEFD相对于EFD,划分的频率区间更加合理,每个频带只包含一个频率峰值,即IEFD在处理含噪信号时比EFD有较大优势。 (a) EFD 随机减量技术(random decrement technique,RDT)是一种利用环境激励下结构响应信号提取自由振动响应的技术。 (10) 设固定值A截取响应u(t),交于不同时刻tk,u(tk)=A(k=1,2,…,n)。从每个tk开始,截取足够长的样本u(t-tk),并将样本u(t-tk)的时间起点tk平移至原点,可得初始值为A的随机子样本函数yi(t) (11) (12) 式中:N为截取的样本数量;y(t)是初始速度为零、初始位移为A的自由振动响应。 希尔伯特变换(Hilbert transform,HT)由Hilbert提出,即为时间系列u(t)和1/πt的卷积,可表示为 (13) (14) 式中:A(t)和φ(t)分别为z(t)的瞬时幅值和瞬时相位,各表示为 (15) (16) 基于IEFD的模态识别由图3所示的步骤组成。第一步,利用IEFD对结构振动信号进行分解,得到振动信号分量及它们的频率值。第二步,利用RDT提取分量的自由振动响应,并利用多个测点的各阶自由振动提取模态振型。第三步,使用HT求得各阶自由振动的瞬时幅度。第四步,通过瞬时幅度自然对数值的最小二乘拟合,由式(17)得到各阶模态阻尼比。 图3 基于IEFD的模态识别方法Fig.3 Modal identification method based on IEFD (17) 式中:ak为阻尼比ζk与角频率ωk的乘积,可通过最小二乘拟合瞬时幅度自然对数值得到。 为了验证模态振型的可靠性,引入模态置信准则(modal assurance criterion,MAC) (18) 式中:φa,j为使用方法a估计的第j阶振型向量;φb,j为利用方法b估计的第j阶振型向量。 本节采用四层框架结构模型以验证提出方法的有效性,该结构如图4所示。结构每层的质量、刚度和阻尼分别为m=100×[20,30,15,30] kg、k=10 000×[15,20,20,30] N/m和c=250×[1,1,1,1] N/(ms)。利用状态空间法得到四层框架模态参数理论值及随机激励下各层振动响应。其中,振动响应的采样频率为50 Hz,采样持续时间为500 s。 图4 四层框架结构Fig.4 Four layers frame structure 利用2.3节描述的步骤,对四层框架进行模态识别。IEFD分解的框架第4层振动响应结果如图5所示。利用RDT得到图5中各分量的自由振动响应,如图6所示。并对其他三层的振动响应同样进行基于IEFD的模态识别,得到的频率和阻尼比平均值如表2所示,模态振型如图7所示。另外,使用SSI-cov对该结构进行模态参数识别,结果同汇总于表2。 (a) 模态1 (a) 模态1 图7 基于IEFD识别的四层框架模态振型Fig.7 Modal shape of four-story frame identified by IEFD 表2 四层框架模态参数识别结果对比Tab.2 Comparison of modal parameter results for the four-story frame 结果表明,基于IEFD的模态识别方法能够准确识别四层框架的模态参数。对于固有频率,SSI-cov和IEFD的结果与理论值基本一致。对于阻尼比,IEFD的结果准确度高于SSI-cov。对于模态振型,以理论值作为计算MAC的参考值,四阶模态振型中最小MAC值为0.996,振型识别准确。 试验桥为一座跨度为109 m的人行斜拉桥。该桥桥塔为单A型塔,42 m高,桥面由锚碇在塔顶的七对拉索支撑。加速度传感器布置如图8所示,从右到左编号为D1~D4。该测试以128 Hz的频率进行了1 h的采样[12]。 图8 全桥立面及传感器布置图Fig.8 Elevation and sensor layout of the test bridge 为了减少激励噪声的影响和计算量,本文选取了该测试中1 000 s~2 000 s段的加速度时程作为处理信号,并利用[0.5,3.5]Hz的带通滤波处理。同样,采用IEFD和SSI-cov对该斜拉桥进行模态识别,并利用快速傅里叶变换(FFT)识别各测点振动响应的频率,四测点平均值如表3所示。图9和图10分别为IEFD处理D4采集振动信号的分量及各分量的自由振动响应。同时对其他三个测点进行识别,表3汇总各测点识别固有频率和阻尼比的均值。其中,采用文献[12]识别的模态振型作为计算MAC值中的参考模态振型。各阶模态振型如图11所示,图中实线为文献[12]的识别结果。 (a) 模态1 表3 斜拉桥模态参数识别结果对比Tab.3 Comparison of modal parameter results for the cable-stayed bridge (a) 模态1 图11 基于IEFD识别的使用试验桥模态振型Fig.11 Modal shape of the test bridge identified by IEFD 结果表明,IEFD能够识别该斜拉桥的模态参数。对于固有频率,除了SSI-cov第三和第四阶模态有差别外,文献[12]、FFT、SSI-cov和IEFD的结果基本一致。对于阻尼比,文献[12]和IEFD的结果基本在同一数量级别,而SSI-cov的第三和第四阶的结果有一定偏差。对于模态振型,IEFD与文献[12]相近,同样,SSI-cov第三和第四阶的结果较差。由于该斜拉桥第三和第四阶模态较为密集,造成SSI-cov产生虚假的第三阶模态,而没识别出自然频率为2.24 Hz的模态。因此,针对该含密集模态的斜拉桥,IEFD较SSI-cov更可靠。 基于EFD无法处理低信噪比信号的缺陷,本文利用AR功率谱鲁棒性强、分辨率高等特点,对EFD进行改进。通过四层框架和人行斜拉桥的模态分析,得到基于IEFD的模态参数识别如下结论: (1) 基于AR功率谱分割的EFD能够处理类似结构环境振动的低信噪比信号,比EFD有较大优势。 (2) 基于IEFD的模态识别方法能够较为精确地识别结构模态参数。 (3) 针对含有密集模态的结构,IEFD方法识别的模态参数较为准确,具有一定优势。
1.3 IEFD与EFD对比


2 基于IEFD的模态参数识别
2.1 随机减量技术



2.2 Hilbert变换

2.3 模态参数识别
3 四层框架模拟验证
3.1 框架基本参数
3.2 框架参数识别




4 实桥测试验证
4.1 测试概况
4.2 参数识别


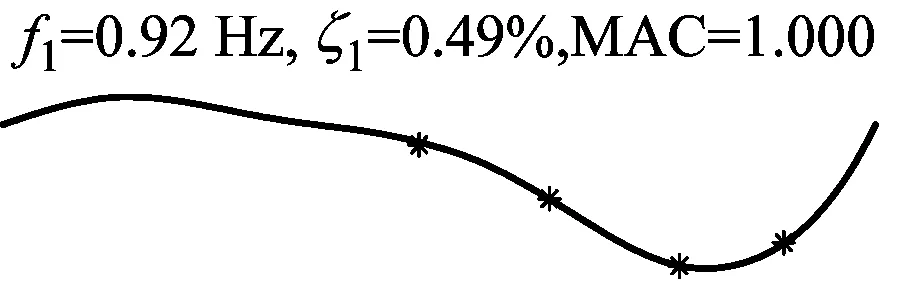
5 结 论

