基于插值与降维方法的输电塔线体系随机脉动风场有效模拟
杨雄骏,黄金山,张建国,雷 鹰
(厦门大学 建筑与土木工程学院,福建 厦门 361005)
输电导线在风致作用下将产生的低频率、高振幅的振动,因此,风荷载是输电塔线体系结构设计必须考虑的重要因素,而随机脉动风场的模拟是输电塔线体系抗风设计的首要任务[1]。关于风场模拟的维度,白海峰等[2]考虑输电塔线体系结构特征与风场特性,将三维风场简化为多个一维风场。沈国辉等[3]对比不同方法的计算一维风场的效率与结果,对不同计算方法的适用性进行了讨论。楼文娟等[4]采用CFD 数值模拟与风洞试验相结合研究山地风场特性对输电线路风偏响应的影响。韩枫等[5]也对输电塔线体系进行了三维多变量脉动风场模拟。
谐波叠加法是模拟脉动风速时程的传统方法,该法虽有理论简单清晰等优点,但计算十分耗时,尤其是当需要模拟的点数较多时,效率变得更加低下[6-7]。在谐波叠加法中,Cholesky 分解与三角级数叠加将耗费大量的计算时间,因此减小二者的计算量十分重要。Yang[8]在模拟过程中引入快速傅里叶变换(fast Fourier transform,FFT)技术,提高了三角级数叠加的计算效率。Ding等[9]在互谱密度矩阵的 Cholesky 分解中引入三次 Lagrange 插值,减少了 Cholesky 分解的次数。罗俊杰等[10]采用三次均匀B样条插值来拟合分解谱密度曲线。Tao等[11]引入Hermite插值建立的分解谱函数矩阵在全频域内的近似函数表达。
另一方面,谐波叠加法在本质上属于Monte Carlo模拟方法,而在Monte Carlo模拟方法中,处理高维的随机变量一直是个难题。需要进行大量的随机抽样才能保证模拟的精度,但是数量巨大的样本不仅增加了随机模拟的计算量,更重要的是,结构动力响应的计算量也随之大大增加。Chen等[12]提出随机谐和函数表示方法,并对频率选点进行了优化。刘章军等[13]通过引入随机函数的约束条件,对脉动风场模拟的谱表示法降维处理。
目前对输电塔-线系统风场模拟的研究中,较少考虑到横风向与竖风向的脉动风的相关性,或未针对输电塔-线系统结构特点对风场进行简化,导致计算效率较低。此外,虽然插值方法在改进Cholesky 分解方面得到了广泛的应用,但是未有将插值方法与脉动风场模拟降维方法相结合的研究。因此本文对于输电塔,主要考虑其顺风向与横风向的脉动风,而且认为其两个方向不存在相关性,将其简化为一维多变量进行;而输电导线需考虑横风向与竖风向的脉动风,并认为两者存在相关性。基于以上研究基础,本文对输电塔进行一维多变量脉动风场模拟,但对输电线进行考虑二维多变量脉动风场的模拟,而且将改进Cholesky分解的Hermite插值和谐波表示法的降维处理技术相结合进行输电塔线体系的脉动风场模拟,提出了一种较现有的输电塔线体系脉动风场数值模拟方法更有效的模拟方法。
1 输电塔线风场体系
在笛卡儿坐标系中空间P点t时刻的瞬时风速U(P,t)由平均风速和脉动风速组成,即
(1)
式中:u、v和w分别表示纵向、横向和竖向风脉动分量;U(z)为纵向平均风速,用指数律分布表示为
(2)
式中:zs为离地参考高度;α为风速廓线指数。
如图1所示的输电塔-线系统中,输电塔是垂直矗立的高耸结构,风场的垂向(Z方向)脉动能量较低,对输电塔可忽略不计,主要分析其顺风响应(X方向)与横风响应(Y方向);而输电导线由于受到沿线路方向(Y方向)的约束作用,而只计纵向(X方向)及垂向(Z方向)脉动作用,且同时考虑这两个方向的相关性,进行二维多变量脉动风场模拟。
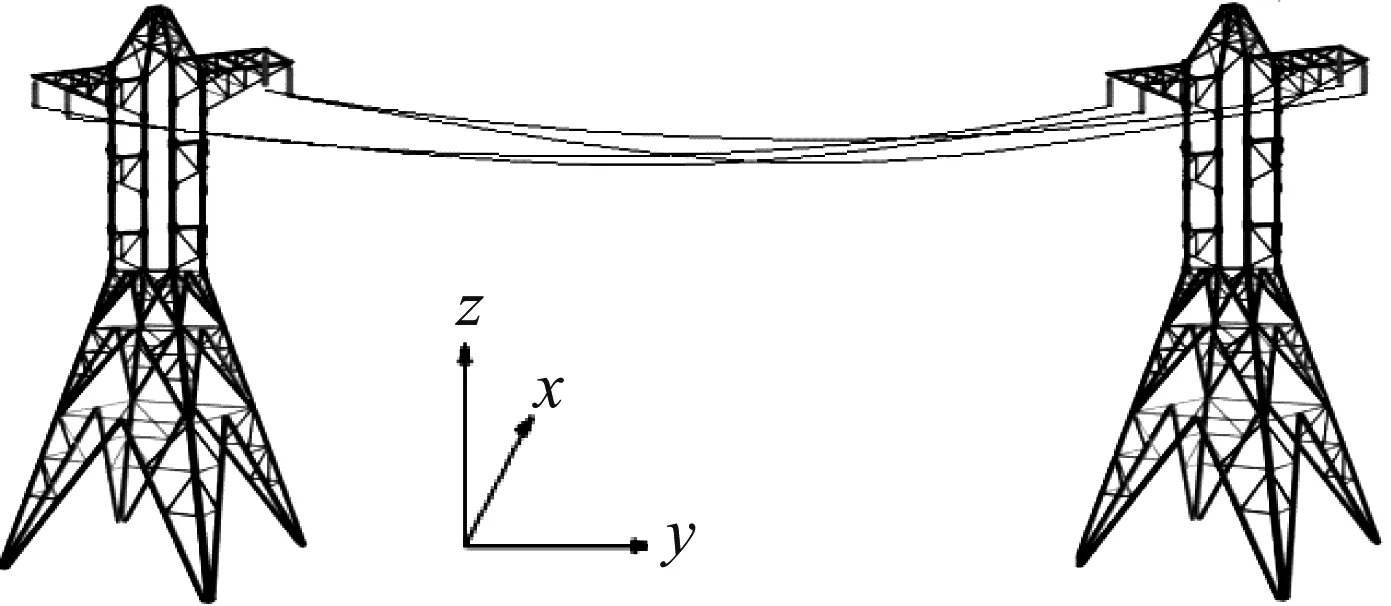
图1 输电塔线体系示意图Fig.1 Schematic of transmission tower-line system
由于输电塔线体系具有高度高的结构特征,采用沿高度变化的风场功率谱密度函数比较符合工程实际。因此对纵向风速谱可采用的Kaimal谱,而对横风向和竖风向均可采用Panofsky- Kaimal谱,其表达式分别如下[14]
(3)
(4)
(5)
式中:u*=KU(z)/ln(z/q0)为摩擦风速;q0为地面粗糙长度;K为Karman常数。
由实测数据可知,横向脉动风速v(t)与纵向脉动风速u(t)及竖向脉动风速w(t)之间不存在相关性,但纵向脉动风速u(t)与竖向脉动风速w(t)之间具有相关性,因此引入纵向脉动风速u(t)与竖向脉动风速w(t)之间的交叉谱密度
(6)
综上所述,对于输电塔,可将风场简化为两个相互独立的一维风速场(X方向与Y方向);对于输电线导线,则需要模拟一个X、Z方向相关的二维风速场。
2 输电塔-线风场模拟方法
2.1 基于传统谐波叠加法及Cholesky分解
2.1.1 输电导线的风场模拟
一组有n个点的二维多变量的平稳高斯随机风场f(t)=[f1(t)f2(t) …fn(t)]T,节点的风速向量空间fj(t)=[uj(t)wj(t)]T。n个点的互功率谱密度矩阵S(ω)可以表示为
(7)
式中,考虑X、Z方向脉动风速相关,每个功率谱矩阵Sij(ω)为 2×2的子矩阵,Sij(ω)可以表示为
(8)
相干函数用来描述脉动风在空间上的相关性。采用Davenport相干函数表达式[15]
(9)
式中:r=x,y,z;s=u,v,w;zi、zj分别为离地高度;Crs为指数衰减系数。
S(ω)为半正定矩阵,进行Cholesky分解可得
S(ω)=H(ω)·H*T(ω)
(10)
式中,H*T(ω)为H(ω)的转置共轭矩阵。
S(ω)为实对称矩阵,故H(ω)为实数矩阵。对某一频率点ω的谱密度矩阵进行分解,可得
(11)
随机过程fj(t)的样本可由下式来模拟[16]
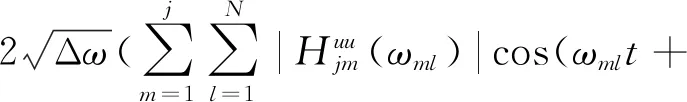
φ2m,l))
(12)
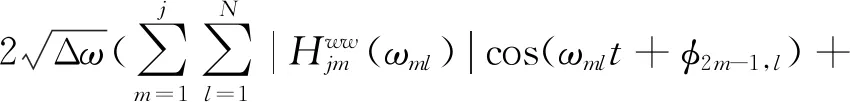
(13)
式中:N为频率等分数,取为足够大的正整数,一般取2的整数次幂;Δω=ωu/N为频率增量;ωu为上界截止频率,即当ω>ωu时S(ω)=0;φ为均匀分布于[0,2π]区间的随机相位角。ωml为双索引频率,其表达式为
m=1,2,…,n;l=1,2,…,N
(14)
2.1.2 输电塔的风场模拟
输电塔的风场模拟的方法与上节输电导线模拟风场方法类似,但纵向风场与横向风场是分别独立模拟。分解的谱密度矩阵S(ω)降为n阶(输电塔线风速谱密度矩阵为2n阶)。以竖向风vj(t)(j=1,2,…,n)为例,对于一维n变量零均值的平稳随机过程vj(t),同样将其进行Cholesky分解
S(ω)=H(ω)·H*T(ω)
(15)
而随机过程vj(t)的样本可由下式来模拟
(16)
虽然运用FFT技术可以加快上述谐波叠加法中三角级数的叠加,然而在随机过程的模拟中,仍需进行大量的Cholesky分解,尤其是对输电导线的风场模拟,需考虑纵向脉动风与竖向脉动风的相关性,所以谱密度矩阵阶数更大,Cholesky分解更加困难,使得风场模拟效率大大降低。由于Hermite插值函数具有较高的准确性,因此本文采用Hermite插值来减少谐波叠加法中Cholesky分解次数,有效进行对输电塔-导线系统风场的数值模拟。
2.2 基于Hermite插值改进Cholesky分解
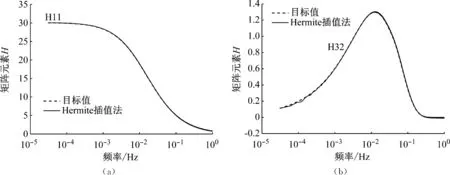
对输电导线或输电塔的数值模拟,仅需在k个插值节点频率及其邻点处进行对互谱矩阵的 Cholesky 分解,而对其他频率点的分解谱函数则采用Hermite插值拟合。这样将传统谐波合成法中的Cholesky分解次数由n×N次缩减为n×2k次(2k< 采用三阶Hermite函数近似表达H矩阵,需要计算插值点处的函数值与其一阶导数值。插值点处的一阶导数值H′(ωi),可利用插值点处的函数值与邻近点ωi+Δω的差商近似。建立区间[ωi,ωi+1]内的Hermite插值函数 a3(ω-ωi)2(ω-ωi+1) (17) a3= (18) 将上述Hermite插值函数引入谐波叠加法,将显著减少互谱密度矩阵S的Cholesky分解次数,插值间距可采用前密后疏指数分布的形式。 要得到可以完备描述n×N维随机变量空间概率信息的样本集,需要从n×N维随机变量空间中采样足够多的样本点。显然,随机变量空间的维度决定了采样点的数量。但是这里存在两个问题,一是从高维空间中采样出具有完备性的样本集相当困难;二是采样效率十分低下。本文采用一种降维方法,可以先在低维随机空间中采样一个完备样本集,再用随机函数映射到高维空间中去,从而达到在高维随机空间中获得完备样本集的目的。 2.3.1 输电塔线风场模拟的谐波叠加法的降维表示 将式(12)、(13)及(16)中的三角函数展开得 cos(ωmlt+φml)= cos(ωmlt)cos(φml)-sin(ωmlt)sin(φml) (19) 式(12)、(13)及(16)中的随机变量φml并没有独立性的要求,它仅存在以下的约束关系[18-19] E[cos(φml)]=0,E[sin(φml)]=0 (20a) E[cos(φml)sin(φm′l′)]=0 (20b) (20c) l=1,2,…,nsel (20d) 为此,可构造一个仅由两个独立的基本随机变量表示所有φml并满足式(20)的随机函数映射 φml(Θ)=m×Θ1+l×Θ2 m=1,2,…,n;l=1,2,…,N (21) 式中,Θ={Θ1,Θ2}为(0,2π)上均匀分布的独立实值随机变量。 由于随机函数映射是确定性映射,为此通过随机函数得到n×N个变量后,还需要随机打乱其排列。这样,每计算一个风场样本均只需要首先从2维的随机变量空间中采样一个点{Θ1,Θ2},然后通过式(22)的变换得到n×N个随机变量,然后打乱排列,再代入式(12)~式(13)或式(16)即可得到一个风场样本。可见,降维表示后,为得到完备的样本集所需要的采样空间维度将大大降低。 2.3.2 基本随机变量的完备抽样 为了获得一个完备的样本集,数论选点法[20]是一个很好的选择。主要包括: (1) 选一个合适的素数nsel作为样本个数 (2) 计算nsel的一个原根a (3) 计算整型向量h h=([1,a])modnsel (22) (4) 计算最优晶格点集 l=1,2,…,nsel (23) 根据数论选点法得到样本集具有完备性,且每个样本的赋得概率均为1/nsel。由于φml与基本随机变量之间存在确定性映射,所以模拟的风场样本的完备性可以得到继承,即风场样本也是完备的,且各样本的赋得概率也为1/nsel。完备的风场样本集可用于风场随机特性和结构可靠性方面的研究。 为了验证所提方法的准确性,进行图2所示模型的风场模拟。输电塔上模拟点位置取在竖向轴线上,每个塔模拟4个点,分别模拟X,Y两个方向的风速,不考虑输电塔之间相干性的影响。输电线模拟点等间距布置,每层每跨均布4点,模拟X,Z方向的风速,考虑各点相干性影响。设计风速U(z10)=30 m/s,风速廓线指数α=0.16,Karman常数K=0.4,地面粗糙长度q0=0.01,上限截止频率ωup=2π,频率等分数N=1 024,M=2N,插值间距Δ=64Δω,时间间隔Δt=0.5 s。 图2 输电塔线体系示意图 (m)Fig.2 Schematic of transmission tower-line system (m) 图3 H矩阵元素插值精度对比Fig.3 Comparison of interpolation accuracy of H matrix elements 选取输电塔第4点与输电线第16点为例,进行统计分析。脉动风速时程曲线如图4所示,模拟风场功率谱与目标功率谱如图5所示,可以看出脉动风能量主要集中于低频,且纵向风谱能量大于横向风谱能量,横向风谱能量大于竖向风谱能量,模拟出的纵向脉动风速也最大,横向脉动风速次之,竖向脉动风速最小,模拟的脉动风的功率谱密度函数与目标值拟合较好。模拟风场互相关函数与目标相关函数如图6所示。在时滞等于0时,相关性达到最大,且纵向风速的相关程度要大于横向风速的相关程度。模拟的脉动风的互相关函数与目标值变化趋势基本一致,都随着时滞增大相关性迅速减小。对功率谱密度与相关函数的误差进行定量分析,以功率谱密度为例,定义误差如下 (a) (a) (a) (24) 表1 样本的功率谱相对误差Tab.1 Comparisons of PSD relative errors 在降维处理方面,本文模拟样本数选取为113,233,383。以样本数113为例,其原根可取为33,由式(22)可知整型向量h=[1,33],随后基于式(23)可获得113×2维的最优晶格点集Θ(133)={Θ1,Θ2}(133)。将Θ(133)={Θ1,Θ2}(133)通过随机函数式(22)变换得到4×1 024个变量后,并随机打乱其排列得到所需完备的随机变量φml(Θ),最后将φml(Θ)代入谱表示式(16)即可得到模拟样本。以第4点为例,表2为生成相同样本数时传统方法和采用插值与降维谱表示法的均值误差及耗时的比较。计算机为:CPU是Intel i5-4 200 H@2.80 GHz、4 G内存,采用MATLAB软件编程。均值误差定义如下 表2 不同数目样本的均值相对误差以及耗时比较Tab.2 Comparison of relative errors of mean and computation time of different numbers of samples (25) 根据模拟结果的统计分析,其统计特征检验符合假定条件。并且和传统谱表示法相比较,在生成相同数目样本时,插值与降维谱表示法不仅可以达到更好的精度,同时耗时也明显减少,表明所采用方法的合理性与高效性。 本文基于输电塔线体系的结构特征和风场特性,对输电塔与输电线分别进行风场模拟。将输电塔风场简化为两个独立的一维风场,而对输电线,引入纵向与竖向交叉谱的影响,模拟一个二维风场。由于传统谐波叠加法中Cholesky需要较大计算量,根据函数曲线随频率的变化规律,采用Hermite插值来拟合Cholesky分解后谱密度曲线,从而提高计算效率。 进一步应用随机函数的约束条件,将传统的谱表示法中的随机变量个数大大减少,实现随机脉动风场的谱表示降维模拟,与传统谱表示法相比,达到相同精度所需生成的代表性时程数量减少。 这样,与目前相关的输电塔线体系脉动风场数值模拟方法相比,本文提出了更高效的模拟方法。通过数值算例分析,表明了本文采用方法能快速准确地模拟出符合要求的多变量随机脉动风场,可为输电塔线体系动力响应分析提供基础。
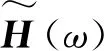
2.3 基于降维的风场谱表示法
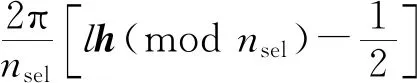
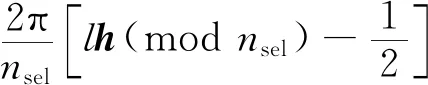
3 数值算例与分析
3.1 数值算例模型
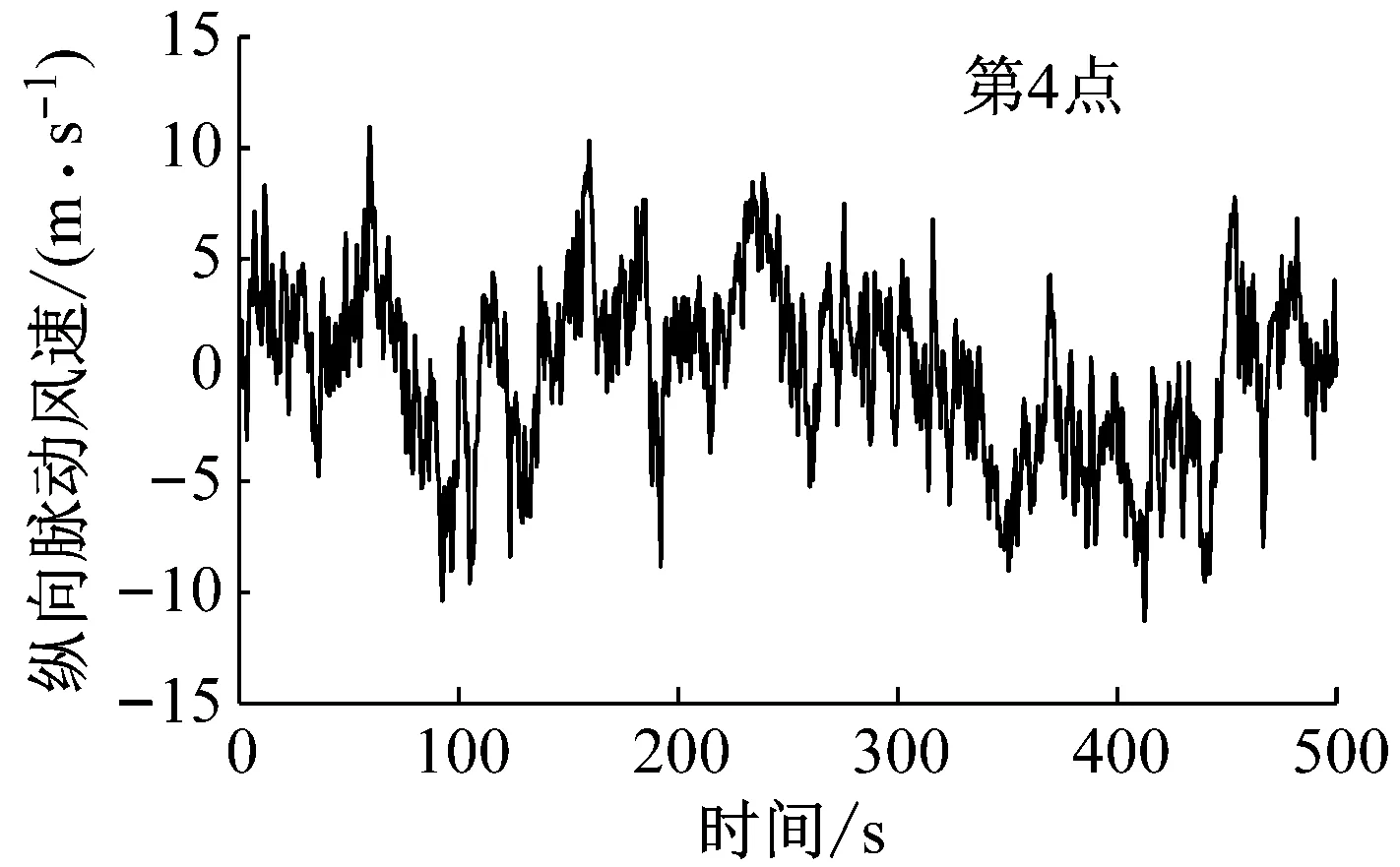
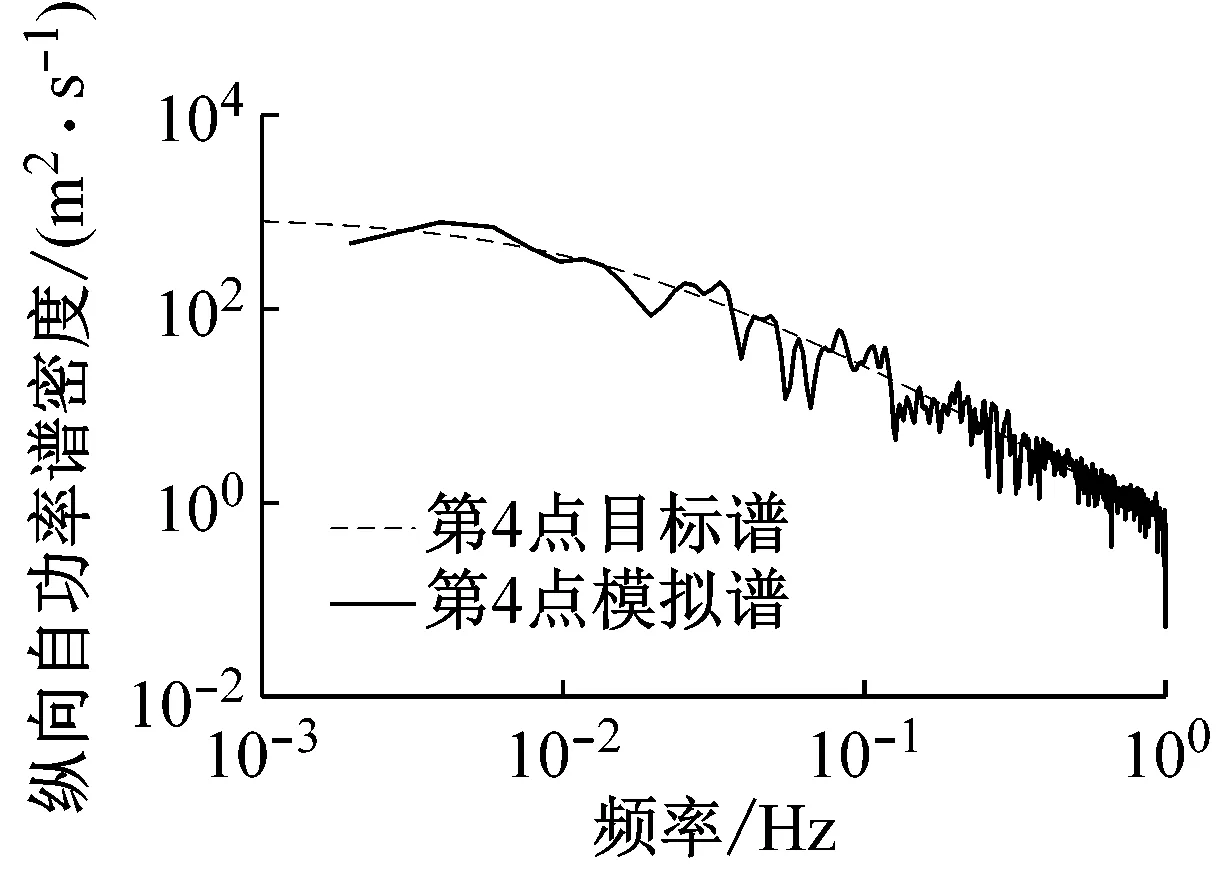
3.2 模拟结果分析
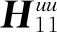


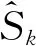



4 结 论

