一类随机递归神经网络的稳定性分析
郭旭晖,姚志易,马维军
(宁夏大学 信息工程学院, 宁夏 银川 750021)
近年来,递归神经网络在组合优化、模式识别等领域得到了广泛的应用[1-3],引起了人们的广泛关注.由于神经网络的动力学行为常常受到随机和时滞等因素的影响,导致系统失稳或震荡.然而在工程应用中要求网络必须是稳定的,因此对于具有时变时滞的随机递归神经网络的稳定性研究,无论是在理论研究还是实际应用中都十分重要.很多学者对随机递归神经网络进行了大量研究[4-5],然而关于其优化问题的研究结果相对较少.到目前为止,还没有关于具有时变时滞的随机递归神经网络逆最优控制的相关研究成果.本文基于逆最优方法和Lyapunov函数,针对一类具有时变时滞的随机递归神经网络模型,讨论了其全局渐近稳定性问题.
1 模型描述
考虑如下具有时变时滞的随机递归神经网络模型

(1)
其中,x(t)=(x1(t),x2(t),…,xn(t))T∈Rn表示状态向量,A=diag(δ1,δ2,…,δn)是一对角矩阵且δi>0,i=1,2,…,n,B=(bij)n×n和C=(cij)n×n分别表示反馈矩阵和时滞反馈矩阵,τ(t)表示时变时滞,f(x(t))=(f1(x1(t)),f2(x2(t)),…,fn(xn(t)))T∈Rn表示非线性激励函数,E是具有适当维数的控制输入矩阵,u(t)为控制输入,σ(t,x(t),x(t-τ(t)))∈Rn×n表示噪声强度函数,ω(t)∈Rn是一个n维独立标准的Wiener过程.
假设激励函数fj(xj(t)),时变时滞τ(t)和噪声强度函数σ(t,x(t),x(t-τ(t)))满足以下条件.
(A1)∀x,y∈R,∃kj>0,使得|fj(yj)-fj(xj)|≤kj|yj-xj|;j=1,2,…,n.
(A2)σ(t,x(t),x(t-τ(t)))是全局Lipschitz连续且满足Tr{σ(t,x(t),x(t-τ(t)))Tσ(t,x(t),x(t-τ(t)))}≤‖M1x(t)‖2+‖M2x(t-τ(t))‖2,其中,Tr表示矩阵的迹,M1∈Rn×n和M2∈Rn×n为矩阵.
(A3)fj(0)=0;σij(t,0,0)=0;i,j=1,2,…,n.
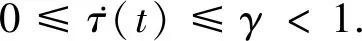
定义[6]对于一般的随机非线性系统
dx=F(x)dt+G1(x)udt+G2(x)dω,
(2)
其中,x∈Rn表示n维状态,u∈Rp表示状态输入,ω∈Rq是一个独立标准的Wiener过程.
如果存在满足以下Hamilton-Jacobi-Bellman(HJB)方程的正最优值函数V(x)
(3)
则
(4)
是可以最小化性能函数的最优稳定控制
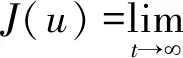
(5)
其中,对于所有的x,q(x)≥0和R(x)≥0.
2 主要结果
在开始证明定理之前,先对Lyapunov函数进行简单计算.
对系统(1)构造如下Lyapunov函数
(6)
由假设(A1-A4)及不等式2xy≤xTx+yTy,利用It可得
≤-δxT(t)x(t)+xT(t)Eu(t)+

(7)
选择控制输入如下
(8)
将(8)代入(7)可得
LV≤-δxT(t)x(t)≤0.
因此,控制输入(8)是一个稳定控制.
根据非线性最优控制,将Lyapunov函数(6)作为最优值函数代入HJB方程(3)可得
(9)
在稳定控制输入(8)的基础上,定义了一个新的控制(即对控制输入(8)进行简单修正),
(10)
其中,λ>2是一个常数.
由(3)和(7)可得
(11)
则
xT(t)[-Ax(t)+Bf(x(t))+Cf(x(t-τ(t)))+Eu(t)]-
(12)
定理对于系统(1),存在正定函数q(x)(12)和严格正函数R(x)(11),使系统(1)通过反馈控制律
(13)
在原点达到全局逆最优,并使性能函数最小化
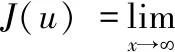
(14)
因此,最优控制律(即控制输入)能使系统(1)达到全局渐近稳定.
证明根据Lyapunov函数(6),系统(1)的无穷小生成元为
(15)
将控制输入(13)代入(15)可得

≤0,∀x≠0.
(16)
系统(1)通过控制器(13)在x=0处达到全局渐近稳定状态.
下面,对q(x)和R(x)进行讨论.
由(12)可得
(M2x(t-τ(t)))-xT(t)[-Ax(t)+Bf(x(t))+Cf(x(t-τ(t)))+Eu(t)]-
(17)
在上述中可知,δ>0,λ>2.则q(x)是正定的和径向无界的.
由(11)可得
(18)
如果|E|≠0,则ETE>0,R(x)>0.通过选择q(x)(12)和R(x)(11),LV可表示为
LV=-q(x)-uTR(x)u+(u-u*)TR(x)(u-u*).
(19)
由文献[7]可得
(20)
根据(16)可得,最优控制u=u*是有意义的成本函数J的最优解.
备注1 本文通过构造适当的Lyapunov函数,给出了稳定控制(10).由于控制器的设计与参数有很大关系,在实际应用中,当激励函数的权值和Lipschitz系数均为常数时,通过选择合适的参数λ,使(11)中的R(x)变为常数,则控制输入(11)就变成了易实现的常数状态反馈控制器.
备注2 在控制工程应用中,最优系统具有许多良好的特性,如稳定性、鲁棒性、降低灵敏度等[8].然而一般随机非线性系统(2)的HJB方程(3)的解很难求得,在很多情况下,HJB方程没有解或不存在唯一解.因此,逆最优方法为求解非线性系统的最优控制问题提供了可能,这种方法的优点是不需要求解HJB方程.
备注3 文献[9]和文献[10]中指出,逆最优控制方法是仿生学神经网络领域最有效的方法之一.然而,在特定任务中优化确切的成本函数并不总是清楚的.因此,如何设计合适的控制器使所考虑的系统达到稳定状态,并使系统的成本函数达到最优,是研究非线性系统稳定性与控制十分重要的课题之一.
3 结论
本文对一类具有时变时滞的随机递归神经网络提出了一种新的全局渐近稳定控制方法.因为求解HJB方程十分困难,很难设计出反馈控制器来实现非线性系统的稳定性.本文基于Lyapunov函数和逆最优方法,我们得到了在逆最优控制下的具有时变时滞的随机递归神经网络的全局渐近稳定控制的充分条件.此外,本文的方法也可以推广到文献[5]的模型.

