迷宫式调节阀节流碟片的流道优化研究

唐腾飞， 肖 莉， 高 翔

(武汉工程大学机电工程学院，湖北武汉 430205)

引言

迷宫式调节阀是流体控制领域常用的节流装置，广泛应用于热力、化工、水循环系统等工业领域。迷宫式调节阀常用于高压差的工作环境，通过迷宫式节流碟片上的流道实现多级降压，降低流体速度，从而保障了整个系统的正常运行。节流碟片是调节阀中的核心组件，同时也是调节阀降低振动、噪声与空化等现象的主要组件，合理设计迷宫式节流碟片，可以显著提升调节阀的性能[1-4]。

迷宫式节流碟片的研究主要热点集中于迷宫式流道的降压级数分布与不同几何形状流道的流动特性研究，并取得了良好的研究成果：李树勋等[5]讨论了节流碟片降压级数在设计过程中的选择；刘来全等[6]在节流碟片上添加了连接槽来改善流动特性；姚伍平等[7]讨论了高温调节阀迷宫式流道的不同参数对流量的影响。

目前，迷宫式调节阀与其降压组件节流碟片研究设计主要以设计者经验为主，主要手段为计算流体力学(Computational Fluid Dynamics, CFD)，基于仿真实验可获得调节阀的整体性能。受限于CFD仿真的操作步骤繁多，多以人工操作来进行相关仿真设置，自动化的仿真优化设计讨论相对较少。另外，在迷宫式节流碟片降压限流过程中，流道内压降变化显著，流体流速在拐角处突变且流速增加，引起碟片振动并可能产生空化，需要合理设计迷宫式节流碟片的几何流道结构来降低上述影响。

本研究提出了一种适用于节流碟片流道的优化设计流程，以流道内流体的最高流速和流量为研究目标，将节流碟片流道的三维几何参数作为输入参数，结合CFD仿真与NSGA-II多目标优化算法，获得可抑制最高流速的同时流量最大化的节流碟片流道优化结构，为相关降压限流元件的优化设计提供研究基础。

1 迷宫式调节阀节流碟片结构与原理

调节阀常在阀体内部放置阀套来抑制高压差等恶劣工况产生的阀体振动、阀体冲刷等问题。以Fisher公司的流量阀为例，阀套放置形式如图1a所示，位于阀芯与阀体内流道相交处。迷宫式流量调节阀的节流碟片组合叠加形成阀套，每级节流碟片上由若干迷宫流道组成，迷宫流道选择平面流道形式，如图1b所示，迷宫流道通常由多个弯道组成。本研究所讨论的迷宫流道由2个直角弯道组成，为多级迷宫流道的典型基础形式，对其研究可为多级迷宫流道的流动特性规律提供参考。

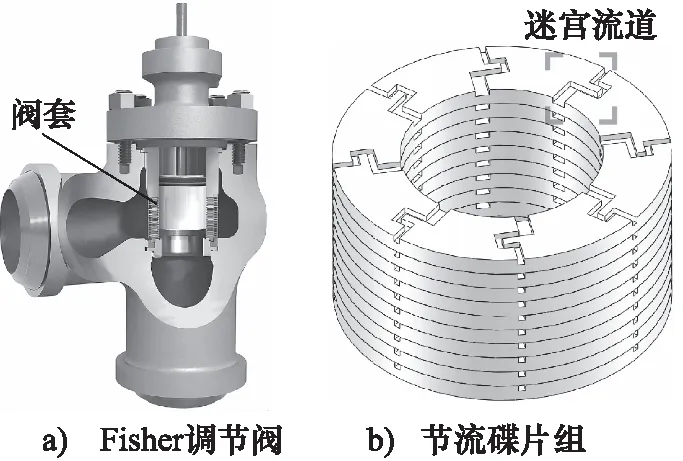
图1 结构示意图

在1片节流碟片上，多个迷宫流道结构相同，因此选取其中1个流道进行分析，如图2a所示，流体从入口进入，经过迷宫流道从出口流出。为方便后续研究，将流道几何参数进行参数化建模，三维流道由流道中心线和流道宽度组成，流道的长为L，宽度的1/2为D，具体参数如图2b所示，共10个参数，取值间隔为0.001 mm，参数的取值范围展示在表1中。流道的深度变化会引起节流碟片组成的阀套高度的变化，受限于调节阀内部空间限制，三维流道的深度一致选择为3 mm。同时，流道的总长度选择为30 mm，因此流道的几何参数L5=30-L1-L3，mm。

图2 流道模型

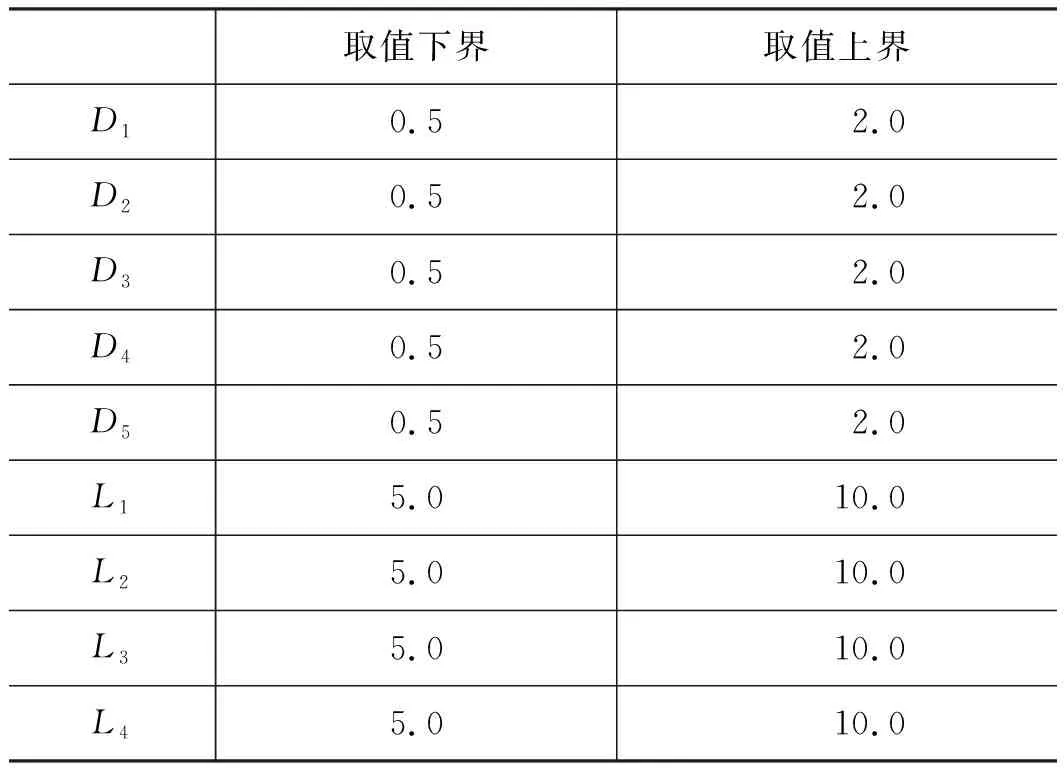
表1 三维流道几何参数取值范围 mm

2 节流碟片流道数值计算模型与仿真结果

2.1 计算模型

本研究的迷宫式调节阀节流碟片的三维几何模型与网格，如图3所示。流道模型的网格通过前处理软件ANSYS ICEM-CFD划分，采用非结构化网格，考虑到模型结构比较简单，网格数量约10万，满足网格独立性要求。需要指出的是，选择非结构化网格而不是结构化网格的原因为，在后续节流碟片优化流程中，非结构化网格自动化生成可靠性更高，且代码编写更简洁。一般来说，流道出口端需要进行延长，保证下游流道充分发展，但本研究关注的重点是流道本身，引入延长流道相当于增加了流道的几何参数L5的距离，从而影响结果，同时L5的变化范围为10～20 mm，约为几何参数L1与L2的变化范围2倍，可以认为出口部分流道已经适当延长，因此本研究中并未增设下游延长流道。

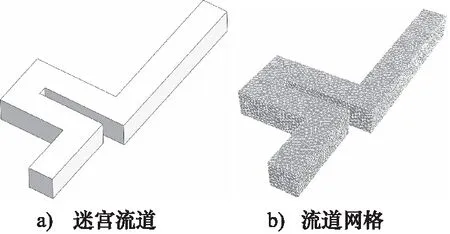
图3 计算模型

数值模拟采用ANSYS Fluent软件，8核并行运算加快仿真速度。流体介质选择为纯水(25 ℃)，入口压力为1.0 MPa，出口压力为0.1 MPa，近壁面边界采用标准壁面函数计算Standard Wall Functions处理方法，模型常数Cμ,Cε1,Cε2分别取0.0845, 1.42, 1.68，流体与外界为绝热，无热交换，壁面边界为无滑移速度边界，湍流模型选择为RNGk-ε湍流模型，同时选用Simple算法二阶迎风格式。

2.2 仿真结果

节流碟片的CFD仿真结果如图4所示，流道中最大速度42.15 m/s，流量1.335×10-4m3/s。在迷宫式流道设计中，满足流量要求的情况下，希望流体的速度尽量越低越好，从而可以降低节流元件的振动，同时可以减少对元件的冲刷。

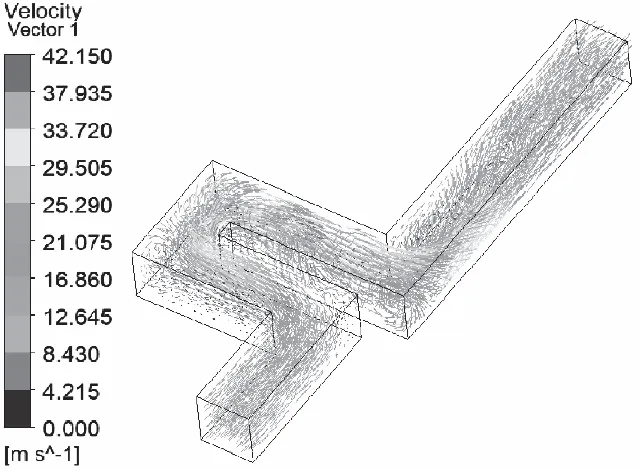
图4 节流碟片三维流道仿真结果

3 节流碟片流道优化流程

3.1 自动化仿真流程

在构建了参数化节流碟片的几何模型，并给出了几何参数的取值范围的基础上，建立节流碟片的自动化仿真流程[8-9]。

节流碟片的三维几何建模选择CATIA软件，可以通过VB脚本实现几何模型的自动化建立；网格建模采用ANSYS ICEM-CFD软件，通过TCL/TK脚本实现网格的划分；CFD仿真采用ANSYS Fluent软件实现，其自动化操作通过IronPython脚本完成；全局控制与数据后处理通过Python脚本实现。整个流程只需要预先设定好几何参数的输入尺寸集合，即可完成节流碟片的CFD仿真并获得结果，如图5所示。与传统人工操作相比较，主要具有2个优点，首先是仿真速度快，几何模型的建立和不同软件的参数设置均在2～3 s 内完成，效率大大提高；其次，在大量重复操作中可以避免操作者因疲劳或疏忽引起的操作错误。

图5 节流碟片自动化仿真流程

3.2 多目标优化流程

以节流碟片的三维流道流动特性中流道内最大流速和流道流量为2个优化目标，其中希望流道内最大流速最小化，流量最大化。这2个优化目标相互矛盾，且2个目标无法比较优劣，因此2个目标的最优解为Pareto最优解。Pareto最优解可以理解为优化过程中，流道内最大流速会逐步降低，同时流量逐步增加，两者均向各自优化目标前进到一定程度后，2个目标无法再同时满足时的目标值。非Pareto最优解具有如下特征，最大流速降低会引起流量减小，或流量增加会引起最大流速增加。

在流道内最大流速和流道流量为优化目标的条件下，节流碟片的三维流道的长度与宽度的参数取值范围为约束条件，采用NSGA-II算法结合CFD自动化仿真流程寻求优化目标的最优解，即Pareto最优解[10-11]。建立的流量Q和最大流速v的数学优化模型可以表示成：

max(Q(L,D),-v(L,D))

(1)

(2)

优化过程中，将最大流速v取反，在优化算法中可以同时寻找流量Q和负值最大流速v的最大值，即可得到流量Q的最大值和最大流速v的最小值。节流碟片流道多目标优化流程如图6所示，主要思想是通过CFD仿真来计算NGSA-II中种群个体的适应度，NSGA-II算法的具体理论可参考文献[12]。

图6 基于NSGA-II的节流碟片流道多目标优化流程

优化过程中，设定种群规模为20，交叉概率0.5，变异概率0.5，最大迭代次数设定为16，加上初始种群数量，一共进行了340次仿真。考虑到CFD仿真耗时较长，因此流程中引入比较数据库，每次新的CFD仿真几何参数与结果会被记录，重复几何参数的结构直接读取CFD结果，减少重复仿真的资源消耗。需指出的是，考虑计算资源和实际工程需求，迭代次数需要综合确定，因此算法不一定收敛至理论上最优，但已获得满足工程目标的最优结果。

4 结果分析

经节流碟片流道多目标优化流程获得了一系列的Pareto最优解，受限于仿真迭代次数的限制，Pareto最优解数量为11，最优解结果如图7所示。Pareto最优解为方块型案例，与非最优解相比较，最大流速v相同时，Pareto最优解的流量Q更大；流量Q相同时，最大流速v的数值更低，说明提出的节流碟片流道多目标优化流程有效的获得了节流碟片的优化结构。

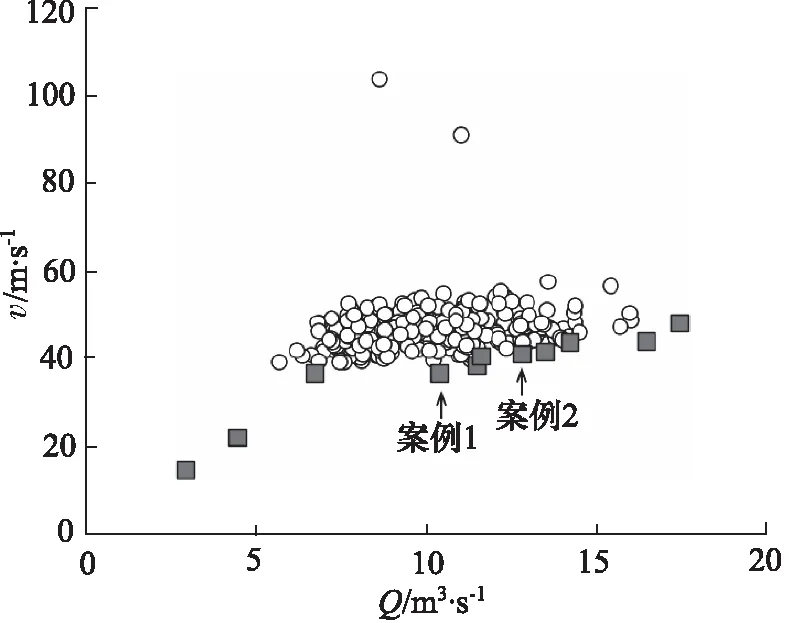
图7 节流碟片流道优化最优解集分布

以图7中案例1、案例2为例，案例1的流量为1.004×10-4m3/s，最大流速为37.667 m/s；案例2的流量1.304×10-4m3/s，最大流速为40.494 m/s，两案例的几何模型与CFD仿真结果，如图8所示。流量增加后，几何模型差异较大，几何参数变量较多情况下难以通过设计者经验来搜寻最优的节流碟片几何结构。最优解集提供了一系列的最优选择，可以按照流量的需求选择对应结构。此外，案例1与案例2中最大流速v与接近流速存在的区域较多，且多在直角拐角附近，控制流体流速需要合理设置直角弯道尺寸来实现逐级降速。比较案例1和案例2的结果，流量增加23%，最大流速增加7%，结合Pareto最优解集，此增长趋势近在流量10×10-4～15×10-4m3/s区间内近似线性，可以为节流碟片的流道设计提供模型选择。

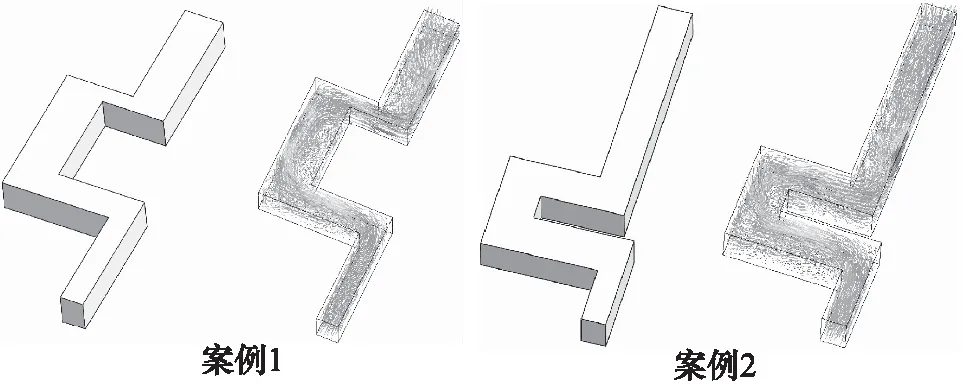
图8 不同案例的几何模型与仿真结果

5 结论

针对迷宫式调节阀的节流碟片流道设计中，几何参数多，难以选择，目标流量与流道最大流速冲突的问题，本研究提出了一种基于NSGA-II算法的节流碟片流道多目标优化流程，可以获得有效降低流体的最大流速并提高流量的节流碟片几何结构集合，为设计者提供模型选择。选择Python语言作为全局控制脚本，实现了节流碟片的自动化CFD仿真流程。将节流碟片的自动化CFD仿真流程与NSGA-II算法联合，获得了的节流碟片最优结构解集。在流量10×10-4～15×10-4m3/s区间内，选择的几何结构流量增加23%，最大流速增加7%，流量增加与最大流速的增加呈近似线性关系。本研究提出的节流碟片流道优化设计流程的可为流体传动元件的设计提供参考。