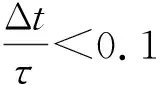一种基于神经网络的磨粒混叠误差修正方法

李彤阳， 洪 葳

(1.中国民航工程咨询有限公司，北京 100621；2.华中科技大学物理学院，湖北武汉 430074)

引言

油液磨粒检测[1-2]已经被应用于旋转机械中，并有效地起到了视情维修[3-5]和延长剩余寿命[6]的作用。由于电感式的磨粒检测基于电磁感应原理，具备非接触和适合于金属管道的优点，基于这种原理的传感器更适合于在线磨粒检测，因此获得了广泛的关注[7]。然而，当多个磨粒同时通过传感器时，会造成磨粒信号产生混叠的现象，将严重影响磨粒检测的精度。同时，相较于图像法和铁谱法，基于电感法的信号混叠问题更为突出。

对于这一问题，钟智等[8]提出一种基于2个传感器不同安装方式的解耦方法；李彤阳等[9]提出一种退混淆的估计方法用于减小检测误差。这些研究探索了混叠问题的解决方法，但是存在对不同传感器的适应能力不足的问题。人工神经网络[10]可以通过特定数据集的训练从而获得特定的模型，这一特点能够很好的解决不同对象的适应性问题，所以被广泛的应用于噪声消除、声源分离等信号混叠问题[11-13]。针对磨粒信号的混叠问题，本研究提出一种基于人工神经网络(ANN)的混叠误差修正方法，通过特定传感器的数据进行训练从而解决修正方法的适应性问题。

1 混叠误差分析

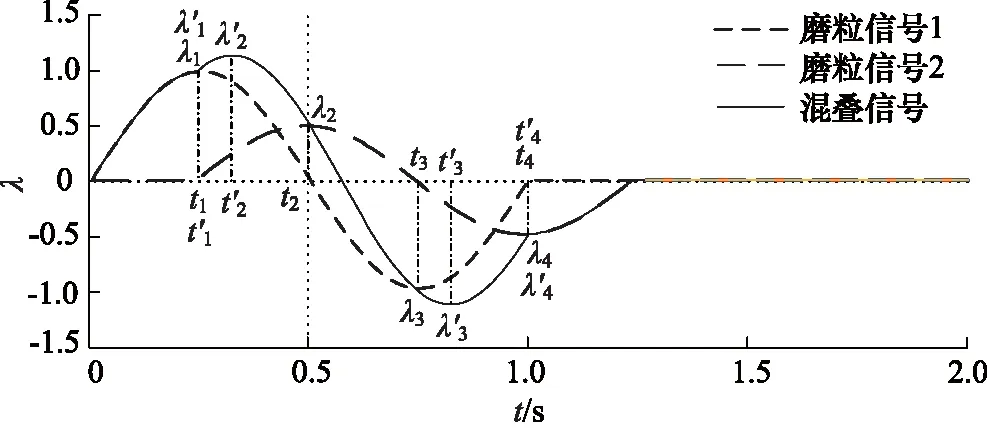
图1 信号的混叠现象

如果想解析的求解混叠问题，则需要准确的获得磨粒信号的波形。将混叠函数记为Ω，则混叠问题可以描述为：

(Λ′,T′)=Ω(Λ,T)

(1)

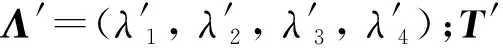
所以，混叠误差即为混叠函数输入与输出之间的差异。为了修正混叠误差，需要获得一个满足式(2)的反映射函数Ω′；然后，通过测量畸变后的参数Λ′和T′可以求出无误差结果Λ和T。

(Λ,T)=Ω′(Λ′,T′)

(2)

然而实际过程中，不同的电感式传感器所产生的磨粒信号具有不同的形状，这会导致Ω和Ω′具有不同的形式，很难通过一个解析模型来解决不同传感器的混叠问题。

2 神经网络修正方法

人工神经网络是一种强有力的建模方法，类似于人脑一样的生物神经网络，其内部是一些计算机模拟的神经元所构成的多层网络，如图2所示，通常包含1个输入层、1个输出层和若干个中间层。通过使用不同的数据集对神经网络进行训练，其中各神经元的输出权重将被调节从而实现对特定问题的适应。对于本研究的混叠问题而言，将传感器实际测量到的信号中所提取的特征参数Λ′和T′作为输入，而真实的磨粒信号中的特征参数Λ和T作为神经网络的输出，对神经网络进行训练，训练后的神经网络就是Ω′的一个近似表达。

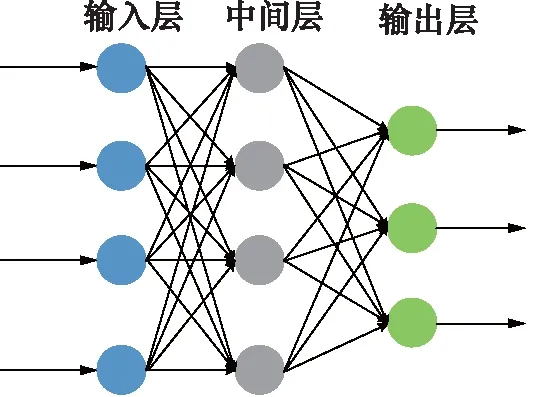
图2 人工神经网络的结构

换而言之，通过特定数据训练的建模方式能够取代数学建模和推导，有益于反映射函数Ω′的建立，而不同传感器所获得的训练数据可以解决方法的适应性问题。本研究提出的基于人工神经网络的修正方法框架如图3所示，包含预处理、训练和解算3个部分。

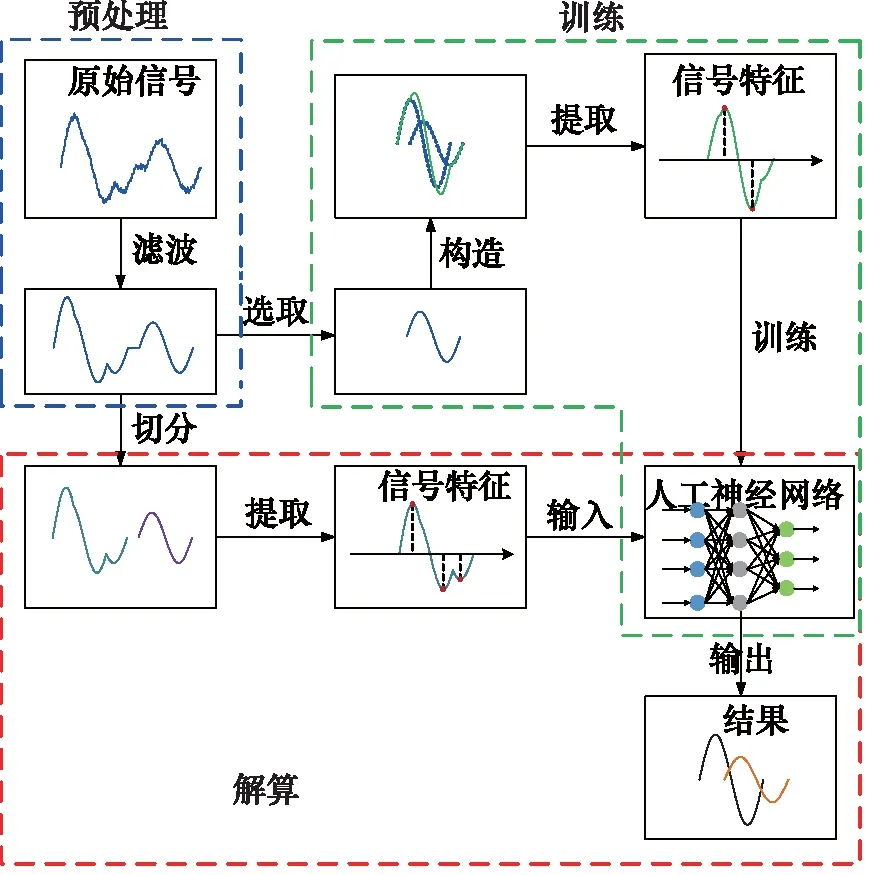
图3 基于人工神经网络的混叠修正方法

预处理用于消除原始信号的噪声、平滑信号以及减少极限点提取的错误。

在训练部分，通过实验波形构造一系列的混叠样本用于训练神经网络，训练部分的步骤如下：

(1) 从滤波后的信号中选取一个完整而且没有混叠的信号曲线作为单个磨粒的原始波形；

(2) 通过复制、缩放和平移原始波形构造一系列的混叠样本；

(3) 提取每个混叠样本中极值点的幅值和相位作为神经网络的输入，同时将构造样本所用的波形的真实幅值和相位作为输出；

(4) 训练人工神经网络。

在解算部分中，将滤波后的信号切分成若干个片段，然后通过训练好的网络解算各个片段中的真实幅值和相位，具体步骤如下：

(1) 通过极值点之间的间距将滤波后的信号切分成一些包含2～4个极值点的片段；

(2) 提取各个片段中极值点的幅值和相位作为训练后的人工神经网络输入；

(3) 通过神经网络解算，估计各个信号片段的真实幅值和相位。

3 仿真验证

为了验证修正方法，2个正弦波被用于仿真多变的混叠情况。在0.2～5之间均匀地选取50个值作为2个信号幅值比例系数λ1/λ2。同时，在0到τ之间均匀地选取101个值作为2个信号的相位差Δt，其中τ为单个信号的周期，由此可以构造5050个混叠信号进行训练和测试。

人工神经网络的重要参数包括：网络的层数、激活函数的形式和隐藏层的神经元个数。由于没有通用的方法来确定这些参数，因此基于经验的选择和测试是通常采用的方法。一般而言，隐藏层为1～2个；激活函数从“Logsig”、“Tansig”和“Purelin”中选取；由于隐藏层的神经元个数与问题的复杂程度有关，因此通常需要测试确定。因此，本研究先将隐藏层的个数确定为20个来测试不同隐藏层的数量和激活函数的差异，然后在此基础上测试不同隐藏层神经元个数的影响，均方差(MSE)作为评估不同参数下人工神经网络性能的指标。采用单隐层的测试结果如表1所示，采用双隐层的测试结果如表2所示。

由表1、表2可以看出，相对于单隐层，双隐层并没有明显的减小训练误差，所以单隐层被用于本研究的混叠问题。同时，采用单隐层中“Tansig”作为隐藏层的神经元以及“Purelin”作为输出层的神经元时具有最小的训练误差，所以基于这些参数进行隐藏层的神经元个数N的测试，其结果如图4所示。

表1 采用不同激活函数的单隐层测试结果 %

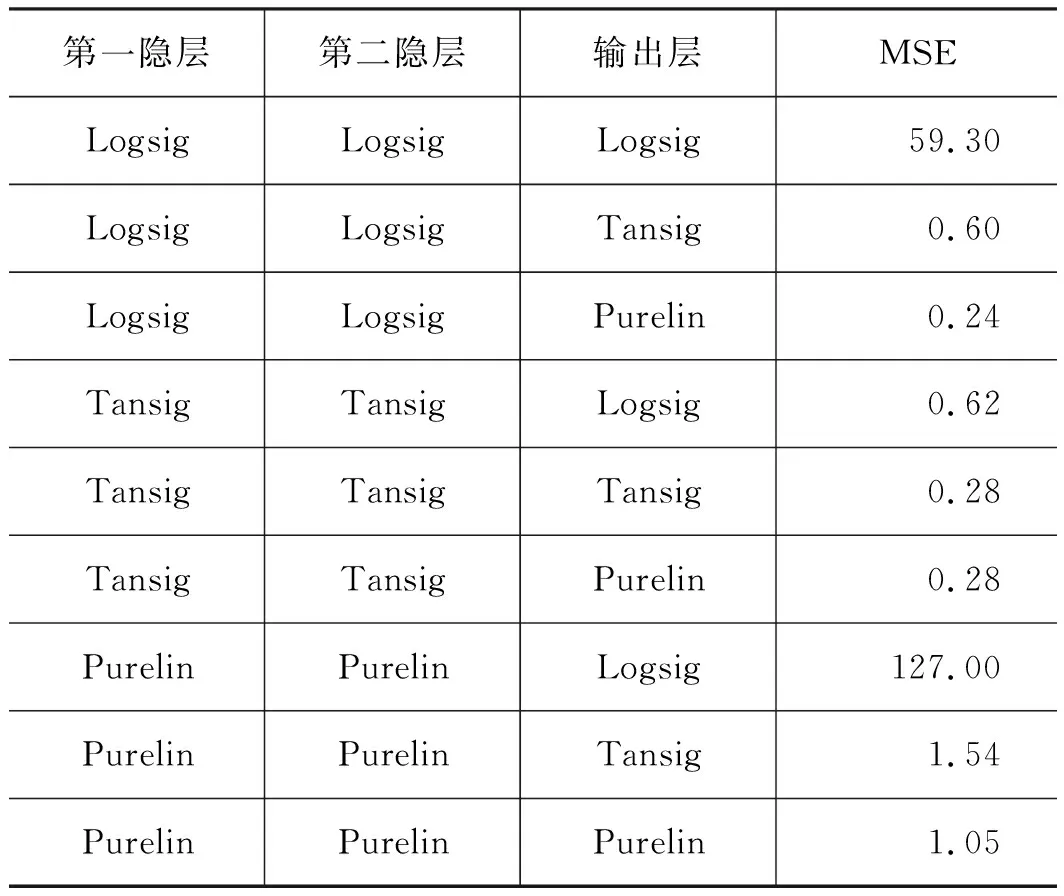
表2 采用不同激活函数的双隐层测试结果 %

图4 不同隐藏神经元个数的训练误差

从图4可以看出，当神经元的个数达到5个以上时训练误差就达到了稳定，也就意味着对于本研究涉及的混叠问题隐藏层的神经元最少需要5个。为了确保网络能够充分地拟合所有的混叠情况，采用10个神经元作为隐藏层，最终采用的网络参数如表3所示。

表3 最终采用的网络参数

表4是基于2个正弦波叠加的5050个混叠信号的测试结果，直接检测是将每个样本中所有的正极值直接求和；修正检测是将经过训练后的神经网络修正的正极值进行求和；误差是与2个原始正弦波的正极值之和进行对比。

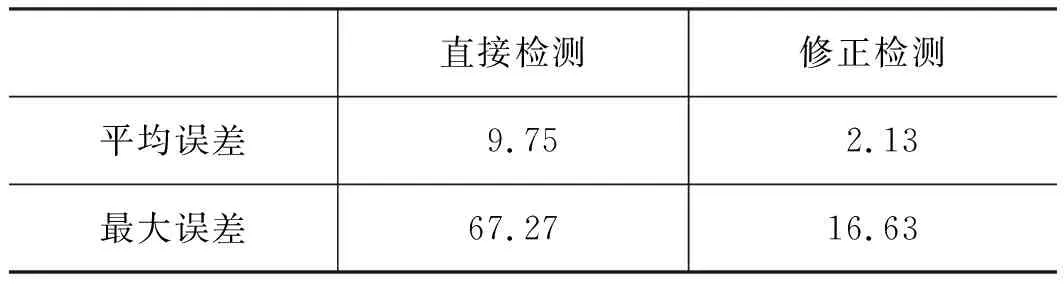
表4 混叠信号的测试结果 %

为了进一步验证修正检测方法的有效性，对比直接检测和修正检测的误差e分布，如图5、图6所示，其中X轴表示原始信号的相位差与信号周期之比，Y轴表示原始信号的幅值之比。

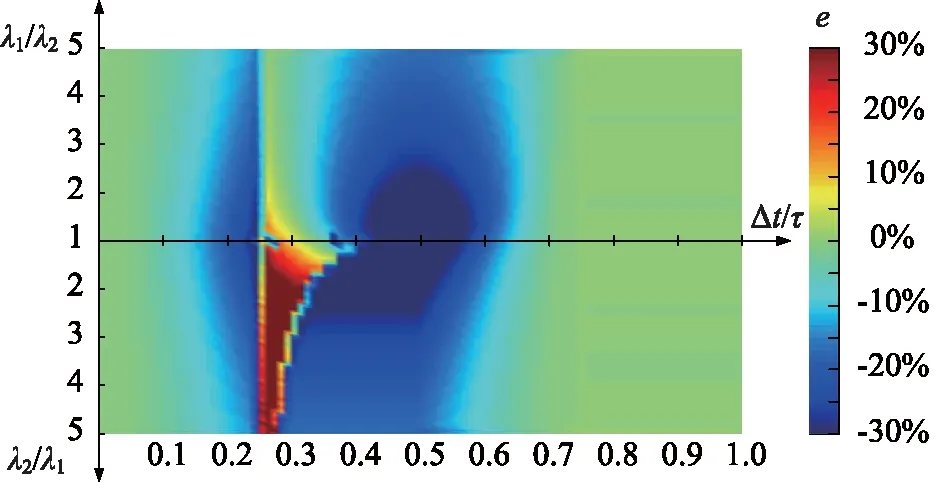
图5 直接检测的误差分布

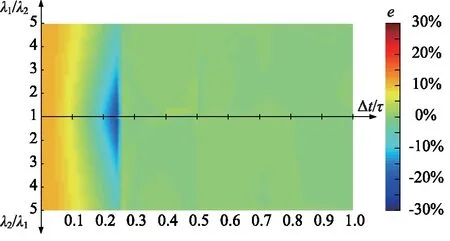
图6 修正检测的误差分布

4 结论