基于IPSO-BP算法的燃油系统气压控制优化

张永贤， 邰万文， 陈杨谨瑜， 李 伟

(华东交通大学电气与自动化工程学院，江西南昌 330013)

引言

在飞机研制过程中，燃油系统地面模拟试验是保证飞机能够正常、可靠、稳定飞行的必要环节，对飞机的飞行工作性能有着直接的影响[1-2]。飞机燃油系统用于储存燃油并在各种规定的飞行状态和工作条件下，确保燃油按需求的流量大小安全地输往发动机，其地面模拟试验为飞机燃油系统提供了设计依据，还能对燃油控制系统的工作状态进行检验。气路压力模拟系统的主要功能是保证飞机在不同姿态下油箱与大气相通，加油时将油箱内的气体排出，避免正压与气泡；耗油时让空气进入油箱，防止真空负压而影响供油。构建一个好的飞机燃油气路模拟系统，是验证燃油系统设计的合理性和优化控制系统精确性的关键步骤。

引气箱压力作为气路控制系统的一个重要执行机构，需为飞机发动机供给任意环境下所需求的气压。地面模拟试验的引气箱压力控制是一种集非线性、时变性、强干扰为一体的电液控制复杂系统，需要设计合理的控制器来对气箱压力进行调节。普通的PID控制器无法达到快速、精确的控制，故利用神经网络逼近非线性函数、结构算法简单易懂的特性，将其与常规PID控制器相结合，通过自学习找到最优的比例积分、微分控制参数，从而提高系统的快速稳定跟踪性。文献[3]中对此研究并发现实际效果并不理想，神经网络的学习时间长、收敛速度慢且连接权重随机初始化，有时导致系统不稳定。文献[4]中提到了一种BP神经学习算法—梯度下降法，不过此算法全局寻优能力不佳，容易陷入局部极值。因此，在前人研究的基础上，本研究提出用改进粒子群算法对BP-PID控制器的参数进行优化，结果表明该控制器能够达到气压控制的预期效果。

1 测试系统组成及工作原理

燃油系统地面模拟试验的引气箱压力控制系统主要由四大部分组成，分别是电液伺服阀、液压缸、节流阀(针型气体调节阀)、气容箱，采用差动控制方法来调节引气箱的压力大小。由于气体的可压缩性，本系统在控制精度方面要求比较高，其中气压动态跟随误差需小于满量程的1%。

地面模拟引气箱气压控制系统结构如图1所示，为了引气箱快速、稳定的达到所需气压，在控制系统中设有稳压箱。引气压力控制系统采用双闭合回路差动控制法，内回路是由阀控对称液压缸控制系统构成，依据控制器的输入信号和伺服系统的位置反馈信号做粗调；外回路是依据引气箱的压力反馈信号和系统预设信号做精调。控制系统的整个工作流程是根据气箱位移传感器的反馈信号与给定信号做偏差，利用基于智

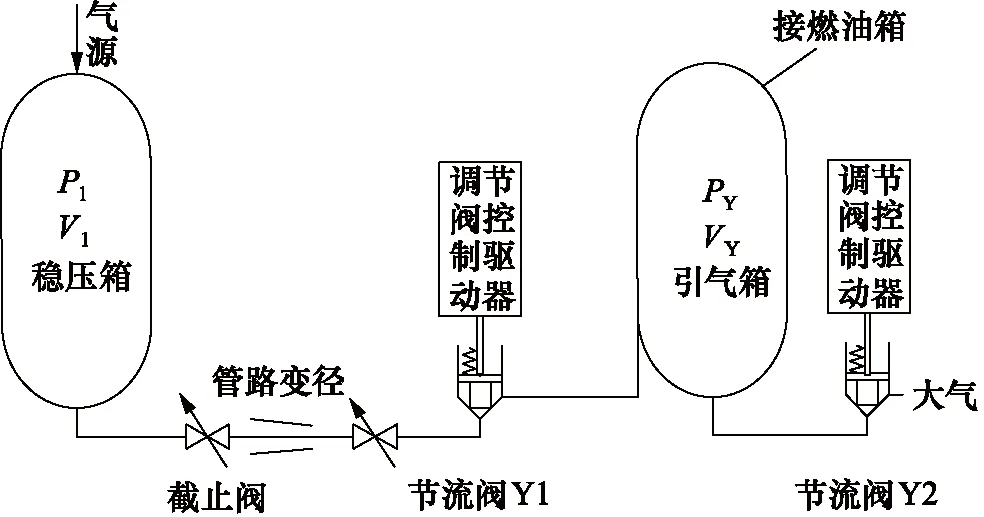
图1 引气箱系统控制系统结构图

能算法的PID控制器得到控制信号，并将其转换成电信号传递给电液伺服系统，最终通过控制节流阀的开度来得到精确的气压值。

2 系统部件模型

2.1 电液伺服系统模型

电液伺服系统在航空航天领域有着非常广泛的应用，具有精度高、响应快、大功率等优点[5]。伺服阀在低频工作时，可将其视为一阶惯性环节：

(1)

同时，伺服阀流量会随着负载变化，其线性化流量方程为：

Qf=KQXf-KCpf

(2)

将式(1)代入式(2)，可以得到：

(3)

式中，Xf—— 伺服阀芯位移

I—— 伺服阀控制电流

Km—— 伺服阀流量增益

T—— 时间常数

KQ—— 流量放大系数

KC—— 弹性系数

pf—— 负载压差

阀控对称缸的流量连续方程为：

(4)

式中，Ctp—— 阀控缸的泄漏系数

Vt—— 作动筒的左右两腔容积

Ey—— 有效体积弹性模数

At—— 活塞面积

Xt—— 活塞移动量

对称液压缸力平衡方程为(不计弹性)：

(5)

式中，mt—— 活塞及惯性负载质量

Bt—— 液压油黏性阻尼系数

FL—— 任意外负载力

将式(3)～式(5)整合化简得式(6)，即为对称液压缸的数学模型：

(6)

式中，Kce=KC+Ctp为流量-压力系数。

2.2 节流阀模型

节流阀的流量大小是依据阀的通流面积来控制的。针型阀在流量控制中应用较为广泛，控制微小的流量时，普通截止阀或其他结构很难实现精确的调节，针型阀可以实现精确的小流量控制[6]。采用针型阀，其流量为：

(7)

式中，d—— 阀座直径

x—— 阀芯开度

θ—— 针型阀的半锥角

α—— 气体流量系数

Q—— 流过针型阀的气体流量

Δp—— 针型阀的端口气压差

推导出：

(8)

对于进气阀来说，阀口的两端压差为稳压箱气压减去引气箱气压和损失压力；对于出气阀来说，阀口的两端压差为引气箱压力减去此刻的外部环境压力。

2.3 气压箱模型建立

凡是能储存或释放气体的空间称为气容[7-8]，根据气体动力学知识可知，气箱容积系数为：

(9)

式中，VY—— 气箱容积

n—— 多变指数，等温过程中，取1

R —— 气体常数

TY—— 容器内气体温度

根据气体理想状态方程：

pYVY=mRTY

(10)

将式(10)两端进行微分变化，得式(11)：

(11)

式中，Qgm，Qcm为进、出气阀质量流量。

当气箱内的气体压力改变时，其温度的变化为：

(12)

式中，c为空气的比热容，取值为1.4；r=pYF/pY0,pYF为气箱的目标压力；pY0为气箱初始压力;TY0为箱内初始温度。

由式(11)、式(12)可得，引气箱的模型为积分环节：

(13)

其中，

(14)

控制系统的器件模型参数数值如表1所示。

表1 控制系统器件基本参数

3 改进型PSO-BP-PID控制器设计

3.1 PSO-BP-PID控制器结构

基于PSO-BP神经网络的PID控制器结构如图2所示，整个控制系统由普通PID控制和PSO-BP神经网络组成[9]。其中，第一部分普通PID控制器负责对控制信号的正向传递，以及直接对引气箱气压进行闭环控制，且比例微分积分控制参数为在线调整方式；第二部分PSO-BP神经网络根据系统的不同状态，以某种性能的最优化，通过粒子群算法对BP神经网络隐含层、输出层的初始加权系数不断地优化更新，得到PID最优化的3个参数Kp,Ki,Kd，从而使系统获得最理想的控制效果。

图2 PSO-BP-PID控制器结构

3.2 改进粒子群算法

假设在一个S维的空间中由N个粒子构成的群体以一定的速度飞行，粒子i在S维空间的位置为Xi=(xi1,xi2,…,xiS)，速度为Vi=(vi1,vi2,…,viS)，是一个潜在的解。整个搜寻过程中，粒子本身寻优的位置记为Pi=(pi1,pi2,…,piS)；群体寻优的位置记为Pg=(pg1,pg2,…,pgS)。每一代粒子找到2个极值后，通过式(15)和式(16)对速度和位置进行更新，最终整个种群的粒子就会逐步趋向于最优解[10]。

viS(k+1)=ωviS(k)+c1r1(k)[piS(k)-xi(k)]+

c2r2(k)[pgS(k)-xi(k)]

(15)

xiS(k+1)=xiS(k)+viS(k+1)

(16)

式中，i=1,2,…,N；k为当前的迭代次数；c1,c2为学习因子，用来调节学习最大步长；r1,r2为介于0～1之间的随机数，为了防止在寻优过程中陷入局部最优值；ω为惯性权重(非负数)，其值的大小影响粒子的寻优强弱。

1) 惯性权重的改进

在标准PSO中，惯性权重为固定值，其值较大，全局寻优能力强，局部寻优弱；其值较小，局部寻优能力强，全局寻优较弱[11-12]。为了满足粒子在前期全局搜索能力强，后期加快粒子的收敛速度，惯性权重的调整如式(17)，这是一种非线性的调整策略：

(17)

式中，ωstart为惯性权重初始值0.9；ωend为惯性权重最终值0.4；kmax为最大迭代次数。

2) 学习因子的改进

在粒子群优化算法中，c1为自我学习因子，其值越大，个体粒子越容易寻找到最优位置；c2为全局学习因子，其值越大，群体粒子越容易找到最优位置[13]。因此，为了能够有效迅速的找到全局最优解，迭代过程中，对c1,c2进行动态调节：

(18)

式中，cstart，cend为加速常数的初始值和终止值，取值范围为1≤cend≤cstart≤4。

3.3 IPSO-BP-PID控制器工作过程

由万能近似定理可知：一个3层的BP网络就可以完成任意维度的映射，即输入层、隐含层和输出层，如图3所示是PSO-BP神经网络的拓扑结构。气压系统的设定值、实际输出值和误差变化量为输入层的3个神经元；隐含层的节点数越多，算法优化时间越长，为保证收敛速度用5个神经元；输出层的3个神经元为Kp，Ki，Kd。因此，本控制系统的神经网络为3-5-3结构。

图3 BP神经网络结构图

用粒子群算法优化BP神经网络的加权系数ωi,ωo来进行地面模拟引气箱气压控制的具体步骤如下：

(1) 根据气箱气压控制系统输入、输出的训练数量来确定网络拓扑结构，对BP神经网络的权值和阈值进行初始化；

(2) 确定种群规模，初始化粒子的速度、位置向量、允许迭代次数及学习因子等；

(3) 依据被控制对象的传递函数，由当前输入值r(k)输出值y(k)及误差值e(k)，从而得到BP神经网络的输入信号，对其进行采样、预处理；

(4) 正向计算BP神经网络的各层神经元输入、输出。输出层对应于PID的控制参数Kp，Ki，Kd为正值，故其激活函数为非负的Sigmoid函数：

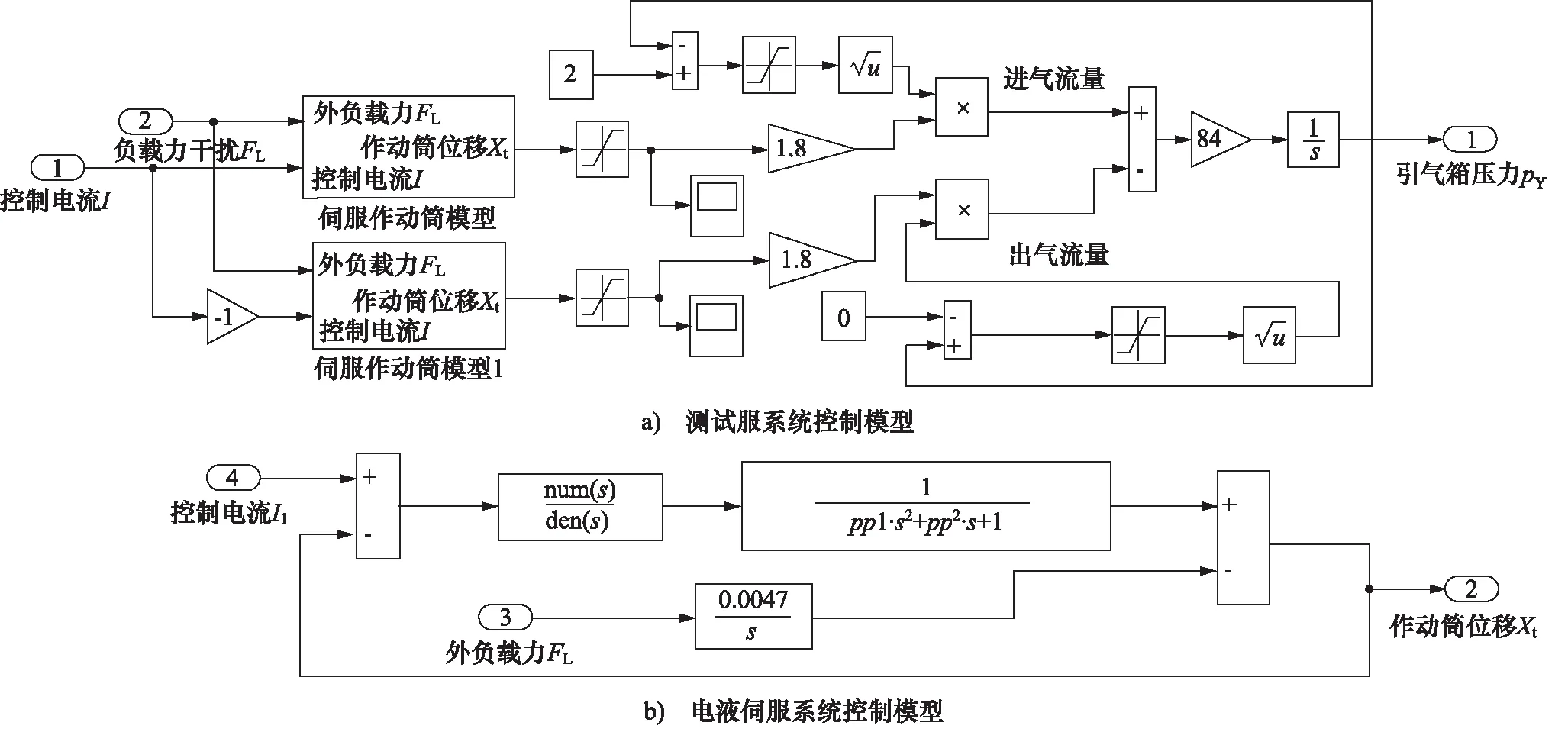
图4 系统仿真模型

(19)

(5) 本系统采用经典增量式数字PID算法，根据式(20)得到控制器的输出u(k)，并将其送入被控对象，对被控系统进行在线调控；

u(k)=u(k-1)+Kp(e(k)-e(k-1))+Kie(k)+

Kd(e(k)-2e(k-1)+e(k-2))

(20)

(6) 评价粒子适应度值F，其值可使用BP神经网络的误差指标计算，目的是判断粒子位置的优良；

(7) 粒子极值更新，比较粒子在每一时刻的个体极值和全体极值，如果比前一时刻的极值好的话，则需要对个体和群体最优值进行更新；

(8) 根据式(15)、式(16)，计算更新每个粒子位置、速度；

(9) 令k=k+1，返回步骤(6)，达到最大迭代次数，寻优结束，输出全局最优值。

(10) 根据得到的最优权值按BP神经网络学习进行训练、测试，获得最佳的Kp，Ki，Kd参数；

(11) 重复步骤(4)、步骤(5)，计算得到最优气压输出值y(k)。

4 系统仿真结果分析

为了比较基于粒子群算法优化的BP-PID控制器和常规的BP-PID控制器对引气箱系统的控制效果，利用Simulink软件对气箱压力控制系统仿真时，搭建的仿真模型如图4所示。

假设引气箱内气体与大气没有热交换，传递过程中泄漏的气体均忽略不计，粒子群算法迭代100次，种群大小为40，改进前后粒子群算法的性能指标IATE的变化曲线，如图5所示。常规PSO迭代到90次时控制系统才收敛，收敛值为6.618；IPSO迭代到80次时就开始收敛了，收敛值为5.219，可以得出IPSO的收敛速度快、精度高。

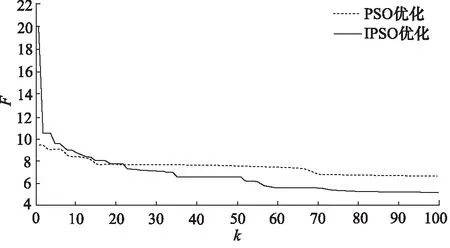
图5 性能指标变化曲线

当对气压控制系统施加单位阶跃信号，可以得到4种控制器下的气箱气压单位阶跃响应曲线，如图6所示，PID控制参数整定曲线如图7所示，系统趋于稳定时，在t=10 s处加入幅值为0.01的干扰量。

从图6、图7可以看出，4种不同的控制器对引气箱的气压控制都起到了一定的控制作用，不过由IPSO优化的BP-PID控制器同其他相比，有更好的性能，调节时间短、稳定性强。在t=10 s时加入了幅值为0.01的扰动量，各个控制器都能做出反应，其中，普通PID控制器和BP-PID有较大幅度的振荡，PSO-BP-PID控制器调节时间长，只有IPSO-BP-PID控制器波动幅度小、过渡时间短。因此，气箱压力控制系统在复杂条件下,IPSO-BP-PID控制器有利于对气箱压力进行实时控制。

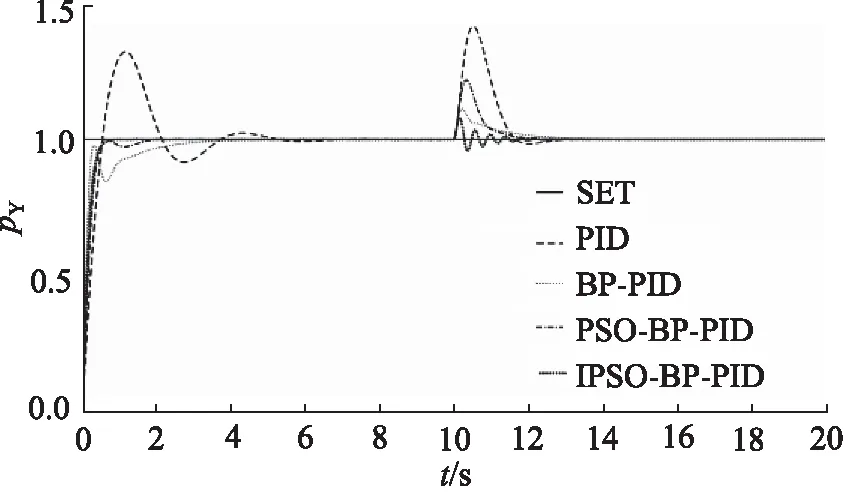
图6 各控制器下的阶跃响应曲线

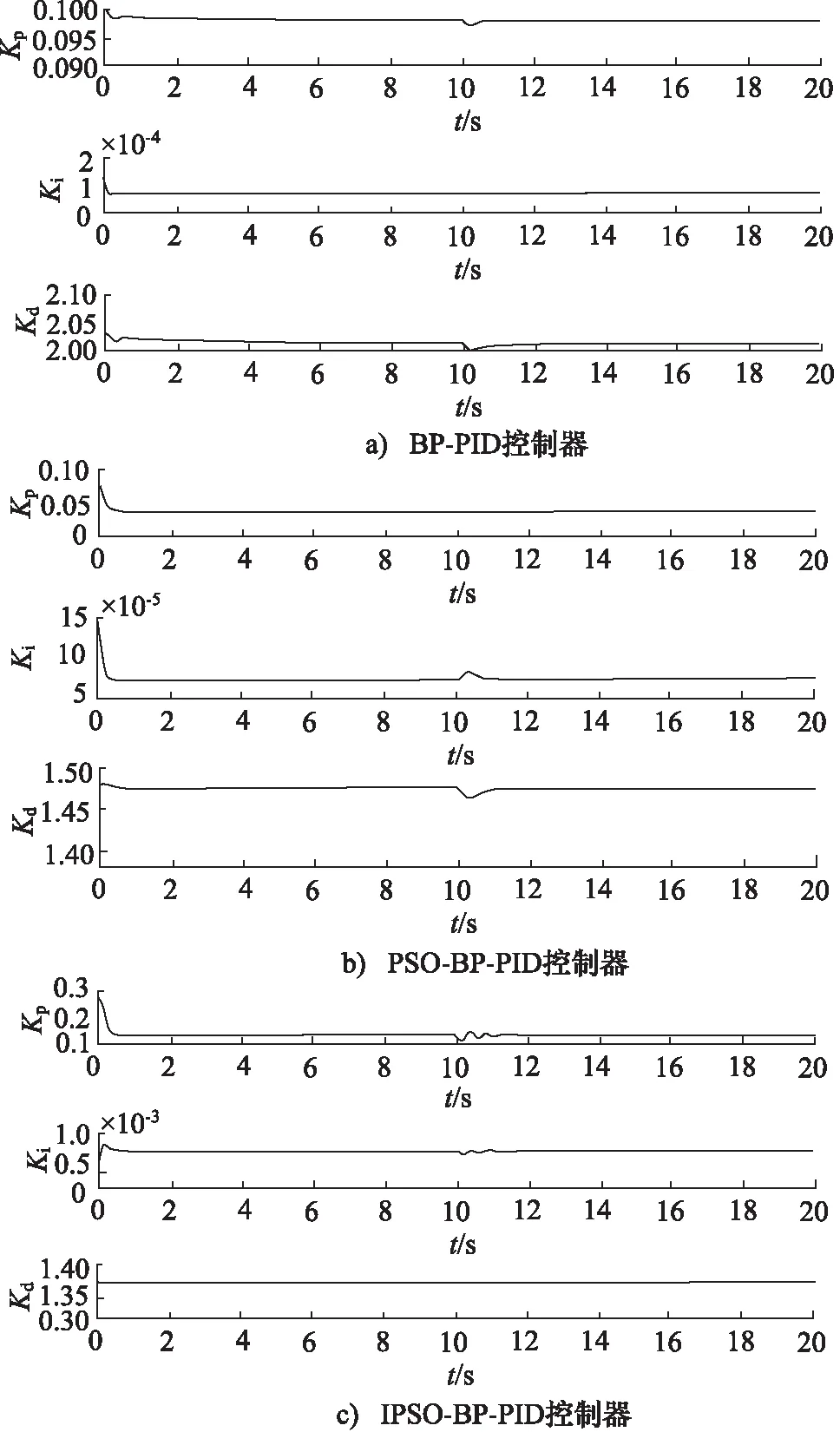
图7 控制参数Kp,Ki,Kd的变化曲线

当对气箱控制系统施加幅值为0.5，频率为0.4 π rad/s的正弦信号时，各控制器下的气压控制响应曲线如图8所示。

图8 各控制器下的正弦响应曲线

从图8中可以看出，由改进的粒子群优化后的BP-PID控制器的气箱压力跟踪响应曲线误差几乎为0，其他的控制器响应曲线相位滞后、跟踪误差较大。通过比较可得，IPSO-BP-PID控制器动态性能好，响应速度快。

5 结论

地面模拟气箱气压控制系统作为时变性、非线性的被控对象，常规的BP-PID控制效果较差。针对BP神经网络在训练过程中易陷入局部极小值的缺陷，本研究采用粒子群优化算法收敛速度快、全局寻优的特性去优化神经网络的初始连接权值，进一步对PID控制器的控制参数在线寻优。结果表明，采用IPSO-BP-PID控制器对引气箱气压进行控制时，在稳定性、精确性和响应速度方面的性能明显优于其他控制器，展现了其良好的性能。