动态调整概率的双重布谷鸟搜索算法

陈 程，贺兴时+，杨新社

1.西安工程大学理学院，西安710600

2.密德萨斯大学科学与技术学院，英国剑桥CB2 1TN

众所周知，随着人类和科技的发展，无论是在工程实践领域还是在研究领域，都会遇到越来越复杂的优化问题。人们使用一些传统的计算方法来解决这些问题时，求解精度以及收敛速度等方面均不能满足实际的需求，且耗时长、成本高。为解决复杂的优化问题，能找到更为合理和满意的近似解，科研工作者设计了大量的启发式算法，而在对自然启发式优化算法的研究中，群体智能算法在过去的二三十年中得到迅速发展，并成为当前最活跃的算法研究领域之一。群体智能算法主要有：萤火虫算法（firefly algorithm，FA）[1]、蝙蝠算法（bat algorithm，BA）[2]、蛙跳算法（shuffled frog leading algorithm，SFLA）[3]、粒子群优化算法（particle swarm optimization，PSO）[4]等。诸多学者也提出许多改进策略：学习因子独立调整策略[5]、自适应交叉策略[6]、早熟扰动[7]等策略，使群体智能算法在解决复杂优化问题时更加有效和高效。

2009 年，剑桥大学的Yang 和Deb 通过模拟布谷鸟寻窝产卵的行为提出了一种新的搜索算法，即布谷鸟搜索算法（cuckoo search，CS）[8]，由于这种算法简单高效、参数少、易于实现、随机搜索路径优等特点，已成功应用于医学图像优化[9]、多目标优化[10]、图像处理[11]、系统设计优化[12]、BT 神经网络（back propagation，BP）[13]、旅行商问题（traveling salesman problem，TSP）[14]等实际问题中。但也存在着求解精度低，易陷入局部最优，收敛速度慢等方面问题，针对这些问题诸多学者也提出了相应的改进方案。王凡等[15]提出了一种在迭代过程中对鸟窝位置加入高斯扰动的方法，它增加了鸟窝位置变化的活力，从而有效地提高了算法的收敛速度。罗东等[16]将函数动态递减因子引入到步长和发现概率中，并对步长和发现概率进行自适应调整，改进后的布谷鸟算法在收敛速度和求解精度方面均有效提高。叶亚荣等[17]在布谷鸟寻找最优鸟窝的时候增加了一个扰动因子，提高算法的收敛速度。王凡等[18]通过分析鸟窝位的群体状态转移过程加入了Markov 链，提高算法全局搜索能力。宋钰等[19]提出了一种基于自适应机制的改进布谷鸟算法，提高了算法的局部和全局寻优能力。贾涵等[20]利用状态判别参数Ps，通过探索-开发平衡状态计算出平衡参数Peb，最终实现鸟蛋的被发现概率Pa的自适应动态调整。但是，对于CS 算法的局部搜索能力弱，易陷入局部最优，算法后期收敛速度慢，求解精度不高等问题，上述改进策略的优化效果仍是有限的。针对CS 算法存在的诸多问题，本文提出了动态调整概率的双重布谷鸟搜索算法（double cuckoo search algorithm with dynamically adjusted probability，DECS），并增加以下策略：将搜索空间分区化，计算种群分布熵确定种群的分布特性，同时与算法的迭代阶数共同决定发现概率P0的大小；通过在寻优过程中引入的新型步长因子以及记忆策略，实现算法双重搜索模式的能力；在随机偏好游走更新公式中，引入了非线性惯性权重对数递减策略及高斯扰动，更大程度地提高鸟窝的探索和开发能力，增强了鸟窝位置的变化活力。通过以上策略，有效改善了布谷鸟搜索算法求解精度低，收敛速度慢，易陷入局部最优的问题。

1 基本的布谷鸟搜索算法

在大自然中，布谷鸟具有特殊的繁衍后代的方式，它们不筑巢，将自己的后代用寄生的方式来养育，通过将自己的卵悄悄地产在其他鸟的巢穴中，由其他鸟为它来卵化和抚养自己的下一代。然而如果宿主鸟一旦发现有外来的鸟蛋，宿主鸟就会抛弃这些外来的鸟蛋或者重新筑巢，为了模拟布谷鸟寻窝和繁衍后代的行为，Yang 和Deb 假设了以下三个理想规则：

（1）布谷鸟一次只产下一个蛋，并且随机选择鸟窝来孵化；

（2）最好的鸟窝将被保留到下一代；

（3）可选择的鸟窝数量N是固定的,宿主鸟发现外来卵的概率Pa∈[0,1]。

基于以上三个理想状态，Yang 等采用式（1）对下一代鸟窝位置x(t+1)进行位置更新：

由式（2）可知，布谷鸟在寻窝过程中，它的飞行路径变化带有重尾的概率分布，使得布谷鸟飞行路径表现出了Levy 飞行的本质，即在寻优路径中频繁的短步长偶尔会出现长步长，使得CS 算法拥有更大的全局搜索能力，也可以有效避免陷入局部最优。

文献[21]采用式（3）计算莱维随机数：

其中，υ和μ服从标准的正态分布，β=1.5，φ=

为了便于对莱维飞行进行计算，采用文献[21]步长因子：

其中，α0为常数，一般取0.01，xbest为当前最优解。

结合式（1）～式（4），CS 算法通过Levy 飞行采用式（5）来更新新的鸟窝位置：

发现概率Pa表示为宿主鸟发现外来鸟蛋的概率，如果发现有外来的鸟蛋，宿主鸟就会抛弃这些外来的鸟蛋或者重新筑巢，即CS 算法通过莱维飞行更新位置后，产生一个随机数r∈[0,1]，若r＞Pa时，则对采用偏好游走的方式生成相同数量的新解。偏好游走如式（6）所示：

式中，γ是(0,1) 区间均匀分布的压缩因子，表示第t代的两个随机解。

2 动态调整概率的双重布谷鸟搜索算法

2.1 动态权重下改变自适应概率P0

在基本CS 算法中固定发现概率P=0.25 不利于全局搜索和局部搜索之间的平衡，因此诸多学者在发现概率中引入了自适应性Pa，使得算法更具有灵活性，自适应Pa是CS 算法重要的参数之一，控制着全局和局部之间的平衡。当Pa值小时，增加了全局的多样性，增强了全局的探索性和开发性。当Pa越大时，加强了局部搜索能力，提高了算法的效率。设立一个合理的Pa可以平衡全局和局部的搜索能力，提高算法的整体性能。在关于Pa的大小控制，国内外诸多学者做出了大量的研究，文献[22]提出自适应布谷鸟搜索算法（adaptive cuckoo search algorithm，ACS），其中自适应性概率Pa的方法如式（7）：

式中，采用文献[22]的参数θ，θ=0.6。自适应性概率Pa方法简单，易实现，但是只考虑到发现概率P随着迭代次数的变化而变化。这样不利于全局和局部的搜索，对一些复杂的、高维的函数求解很难适应。因此在考虑发现概率Pa随迭代次数变化的同时，也应该考虑到每次迭代种群分布情况。发现概率P0的大小由自适应性Pa和空间种群分布位置分布信息共同决定，如式（8）：

式中，Gi是惯性权重的变异算子，其大小由解空间中种群分布的位置情况来决定。

因此本文采用文献[23]提出的分布熵来表达，如式（9）：

式中，j=1,2,…,K，K是解空间Ω被等分划分的个数；N是布谷鸟的总个数；nj是每次迭代后每个等分子空间中布谷鸟分布的个数。

Si表明种群分布情况。每次迭代后Si越大，说明布谷鸟越分散，Gi应该赋予一个较小的值，使发现概率P0越小，加强全局搜索能力。反之Si越小说明布谷鸟越集中，Gi应该赋予一个较大的值，使发现概率P0越大，加强局部探索能力。Gi的具体表达式为式（10）：

其中，Sd=lnK是种群分布熵的上界，即为在平分的解空间Ω中，每一个子空间中有着相同数目的种群个数；Sc是种群分布熵的下界，即为在被平分的解空间Ω中，N个布谷鸟全部分布在其中的某一个子空间Ωj中；δ是参数。

当布谷鸟全部集中在某个子空间Ωj时，由式（10）可得Gmax=δ，经大量实验测试[24]，P0max=0.55 为最佳取值。由式（8）可得，因此参数δ取值为0.751 3。

2.2 自适应双重搜索莱维飞行

基本的布谷鸟搜索算法中的莱维飞行机制，在寻优过程中偶尔出现的大步长，虽然增强了全局搜索能力，但是还是会存在陷入局部最优的情况。步长因子α一直较大，全局搜索能力强，无法获得高精度的解。步长因子α一直较小，算法要达到高精度的解时，就要付出更多的迭代次数，算法的效率低下。针对以上问题，本文提出了自适应双重搜索莱维飞行机制。步长因子由固定的α改为随迭代次数增加而变化的动态变化步长因子ω，如式（11）：

改进的莱维飞行更新公式（12）为：

式中，ti是当前迭代次数，tmax是最大迭代次数，ϑ为参数。

ω1=因子动态变化范围[0,0.367 9]，使动态因子ω变化在[0,1]范围内，由式（11）得ϑ=，ϑ取值为2.718 3。

式（11）中ω在（0,1）之间的随着迭代次数增加的变化如图1。

Fig.1 Factor ω curve图1 因子ω 变化曲线

由图1 可知，在DECS 算法中前期，由于记忆策略引入到Levy 飞行搜索机制中，即用上一代鸟窝反馈位置信息决定下一代鸟窝位置，实现种群由子空间Ω1,Ω2,…,Ωk到整体解空间Ω进行Levy 飞行机制搜索过程，整个解空间种群分布信息决定Gi值的大小，使得DECS 算法前期的多样性更强。DECS 算法中后期种群全局探索能力逐渐减弱，局部开发能力增强，实现双重搜索机制。发现概率P0与双重搜索形成了一个互补的状态，使得DECS 算法有效克服了易陷入局部最优的缺陷，提高算法性能。

2.3 对数递减惯性权重偏好游走

在基本的CS 算法中，偏好随机游走对全局搜索能力和局部搜索能力起着平衡作用，新的鸟巢位置采用固定的上一代鸟窝位置信息，容易造成算法迭代后期陷入局部最优。惯性权重策略可以提高算法的搜索能力，平衡局部搜索和全局搜索之间的关系，因此本文在偏好游走的更新位置中引入了对数递减惯性权重κ，如式（13）：

式中，rmax是惯性权重最大值，rmin是惯性权重最小值；取参考文献[24]rmax=0.1，rmin=0 。ti为当前迭代次数，tmax为最大迭代次数；ξ为对数压缩系数，N(μ,σ)是高斯扰动。惯性权重κ前两项利用对数递减的特性，随着迭代次数的增加而减小，而第三项利用高斯扰动，使得惯性权重κ更具有灵活性。

偏好游走更新公式更新为式（14）：

式中，κ是对数递减惯性权重；γ是（0,1）区间均匀分布的压缩因子；表示第t代的两个随机解。

在DECS 算法中，偏好游走位置更新引入了对数递减惯性权重的策略，使得布谷鸟算法在寻优前期较为完整保留上一代鸟窝的信息，有利于跳出子空间Ωj中的局部最优。随着迭代次数的增加惯性权重的减小，布谷鸟算法在寻优后期，有效削弱了上一代鸟窝的保留信息，更有利于跳出全局局部最优解。

2.4 DECS 算法的流程

动态调整概率的双重布谷鸟搜索算法（DECS）着眼于对算法整体优化，充分利用新型步长因子、发现概率P0和随机偏好游走搜索方式三者之间的关系。DECS 算法前期利用新型步长因子和种群位置更新的记忆策略，保证种群在子空间中充分勘探和寻找最优解的效率；与此同时发现概率P0中引入的种群分布熵，确保了P0在整个迭代期保持着一个动态变化的状态，使得算法更具有活力，增强了算法前期鸟窝的多样性，提升了全局搜索能力，也兼顾了算法后期局部开发的能力。DECS 算法的步骤如下：

步骤1初始化设置：最大迭代次数t，布谷鸟的个数N，解空间划分个数K，发现概率Pa，搜索空间的维数nd，搜索上下界。初始化鸟窝位置，算出每个鸟窝的适应度值fi=f(xi)，i=1,2,…,N，得到最好鸟窝位置，最优的适应度值fmin。

步骤2保留最好的鸟窝位置，按式（12），对每一个鸟窝进行Levy 飞行位置更新，得到一组新的鸟窝解，并计算新的适应度值，与上一代鸟窝位置进行比较，适应度值优的位置替代适应度值差的位置，得到一组较优的鸟窝位置

步骤3通过种群的分布情况计算出当前第t次迭代的发现概率Pa，与随机数r进行比较。若r＞Pa，则用式（14）进行偏好游走搜索方式，淘汰鸟窝数量相同的新解。

步骤4计算出淘汰的新解的适应度值，与Gt=的适应度值进行比较，适应度值优的位置替代适应度值差的位置，得到一组较优的鸟窝位置

步骤5找出中最好的鸟窝位置和最优的适应度值fmin。

判断是否满足终止条件，若满足则停止搜索，输出全局最优值fmin，否则，重复步骤1～步骤4 进行迭代搜索。

3 仿真实验

为了验证DECS 算法的寻优性能，本文选取了19个不同难度的测试函数，如表1 所示。同时与基本的CS算法、花粉算法（flower pollination algorithm，FPA）[25]、BA 算法以及自适应步长布谷鸟搜索算法（adaptive step-size cuckoo search algorithm，ASCSA）[26]四种算法进行了比较，针对不同算法独立运行50 次。其中f1(x)～f7(x) 为多峰函数，f8(x)～f12(x)为单峰函数，维数D=10,50,100。f13(x)～f14(x)为固定维度单峰函数，f15(x)～f19(x)为固定维度多峰函数，维数D=2。记录每次测试结果并计算平均值、最佳值、最差值、标准差。

3.1 测试环境及算法参数

实验环境如下：CPU 为i5-4258U 2.4 GHz，运行内存4 GB，操作系统Windows10，编程环境Matlab r2016。CS 算法、FPA 算法、BA 算法、ASCSA 算法种群数目为25，迭代次数1 000次，其他参数见表2所示。

3.2 算法求解精度比较分析

算法求解精度比较如表3～表21 所示。

本文运用5 种算法对19 个测试函数进行了比较，分别在相同的测试环境下运行了50 次，f1(x)为复杂的多峰函数，拥有无数局部极小值和局部最大值，常常导致算法在求解时陷入局部最优。由表3 可见，DECS算法在求解精度上和稳定性上远远高于其他4种算法，在后期求解时却陷入了局部最优8.881 8E-16。f2(x)函数为典型的非线性多模态函数，它的局部极小值的个数与维数成正比且跌宕起伏不定，由表4 可见，其他4 种算法随着维数的增加寻优能力减弱，DECS 算法却表现出显著的寻优能力，均可以寻到全局最优。f3(x)是典型多模态函数，搜索空间大并拥有许多局部极小点，通常被认为是智能算法很难求解的问题。由表5 可见，DECS 算法均可收敛到理论最优值，表现出了较好的搜索能力和跳出局部最优的能力。f4(x)～f7(x)为复杂的多峰函数，DECS 算法也表现出显著的寻优能力，均可以寻到全局最优。CS 算法、FPA 算法、BA 算法、ASCSA 算法却无法获得全局最优点，在精度上DECS 算法表现出了卓越的性能。DECS 算法在维度增加的过程中，仍然表现出卓越的搜索能力和稳定的收敛性。CS 算法、FPA 算法、BA 算法、ASCSA 算法随着维度的增加，求解精度也明显下降，且无法寻找到全局最优点。ASCSA算法与DECS 算法相比较，在10 维的情况下，有着寻优精度上的差别，但是在50 维和100 维的情况下，ASCSA 算法却无法寻找到全局最优。f8(x)～f12(x)均为单峰函数，f9(x)函数由于它的全局最小值附近函数变化极慢，因此常被用于评价算法的后期搜索性能。f12(x)函数常用于检查算法的寻优能力。DECS算法在10 维、50 维、100 维情况下，均可收敛到理论最优值。对于二维函数f13(x)～f19(x)，DECS 算法均可收敛到理论最优值，对于f15(x)、f17(x)、f18(x) 函数ASCSA 算法和FPA 算法也均可收敛到理论最优值，但在标准差上DECS 算法优于ASCSA 算法和FPA 算法，表明DECS 算法在寻优稳定性方面优于CS 算法、FPA 算法、BA 算法、ASCSA 算法，且表现出更强的鲁棒性。

Table 1 Test functions表1 测试函数

Table 2 Algorithm parameter settings表2 算法参数设置

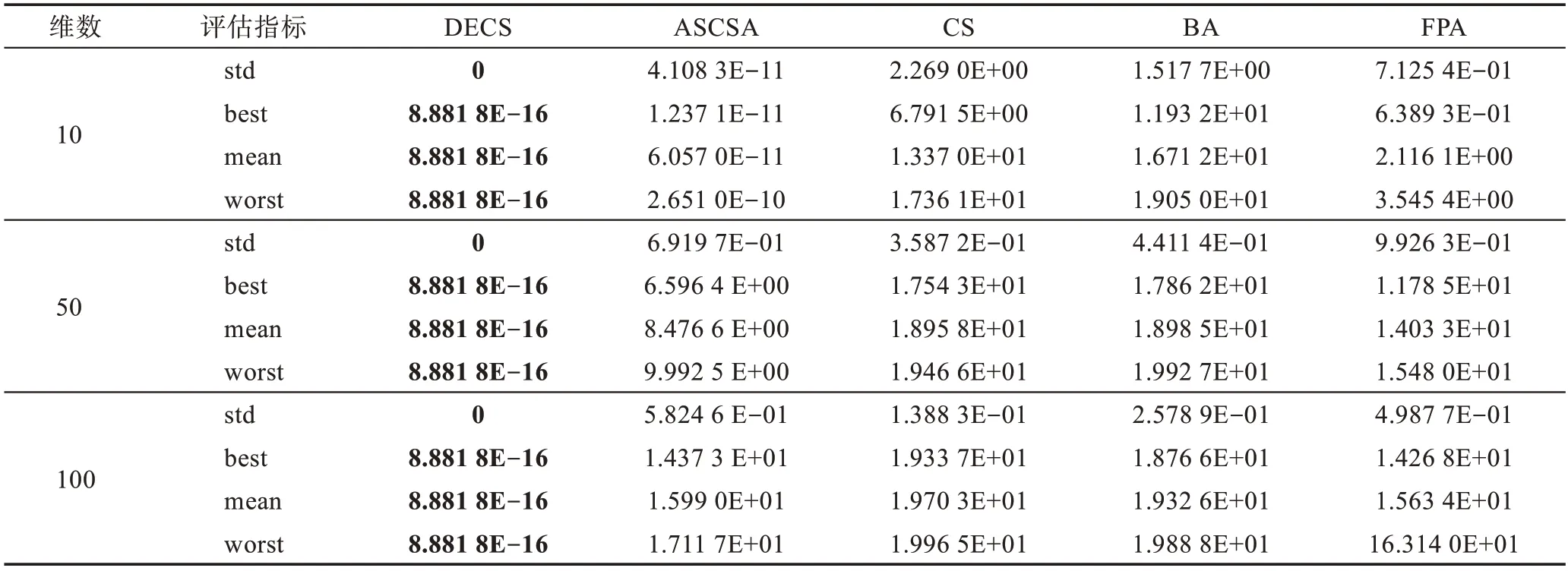
Table 3 Simulation results of f1(x)Ackley function表3 f1(x)Ackley 函数仿真结果

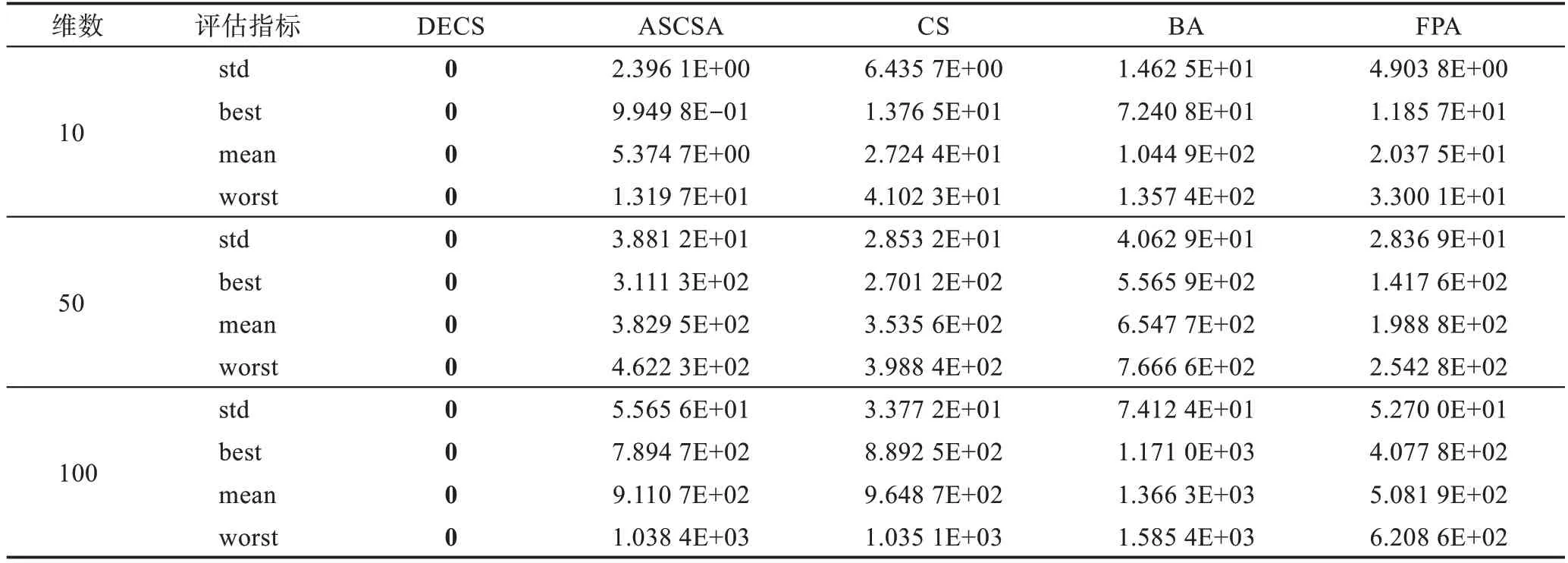
Table 4 Simulation results of f2(x)Rastrigin function表4 f2(x)Rastrigin 函数仿真结果

Table 5 Simulation results of f3(x)Griewank function表5 f3(x)Griewank 函数仿真结果

Table 6 Simulation results of f4(x)Zakharov function表6 f4(x)Zakharov 函数仿真结果

Table 7 Simulation results of f5(x)Alpine function表7 f5(x)Alpine函数仿真结果

Table 8 Simulation results of f6(x)Exponential function表8 f6(x)Exponential函数仿真结果

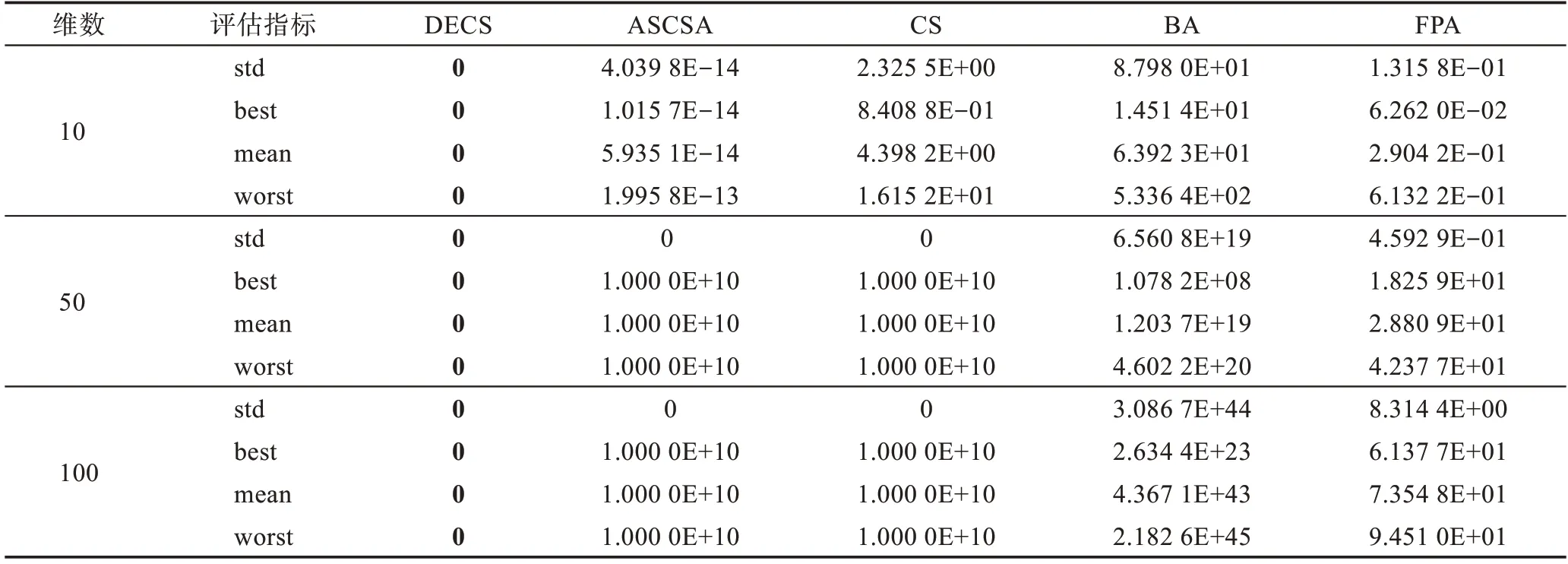
Table 10 Simulation results of f8(x)Schwefel 2.22 function表10 f8(x)Schwefel 2.22 函数仿真结果

Table 11 Simulation results of f9(x)Sphere function表11 f9(x)Sphere函数仿真结果

Table 15 Simulation results of f13(x)Beale function表15 f13(x) Beale函数仿真结果

Table 16 Simulation results of f14(x)Booth function表16 f14(x) Booth 函数仿真结果

Table 17 Simulation results of f15(x)Goldstein&Price function表17 f15(x) Goldstein&Price函数仿真结果

Table 18 Simulation results of f16(x)Bohachevsky function表18 f16(x) Bohachevsky 函数仿真结果

Table 19 Simulation results of f17(x)Easom function表19 f17(x) Easom 函数仿真结果

Table 20 Simulation results of f18(x)Branin function表20 f18(x) Branin 函数仿真结果

Table 21 Simulation results of f19(x) Shubert function表21 f19(x) Shubert函数仿真结果

3.3 算法收敛曲线分析

图2～图20 分别是5 种算法f1(x)～f19(x)的收敛曲线图，直观地反映出了5 种算法的收敛速度和收敛精度。图2～图13 是维数D=10，f1(x)～f12(x)函数收敛曲线图，图14～图20 是维数D=2，f13(x)～f19(x)函数收敛曲线图。在D=10 维测试情况下，由图2～图13可知，DECS 算法在收敛速度上优于CS 算法、FPA 算法、BA 算法、ASCSA 算法，且几乎在100 代之内可以收敛到全局最优，表明DECS 算法具有较快的收敛速度和较好的收敛精度。f2(x)～f7(x)、f15(x)～f19(x)为多峰函数且存在多个局部极小点，测试算法的跳出局部最优和寻优能力。由图3～图8，图16～图20 可以看出DECS 算法具有较强的寻优能力，克服了易陷入局部最优的缺点。f8(x)～f14(x)为单峰函数，测试算法的收敛速度。由图9～图15 可以看出DECS 算法在100 代以内可以收敛到理论最优值。通过对这5 种算法的收敛曲线比对分析可知，无论是高维、低维还是单峰或多峰函数，DECS 算法都具有较好的寻优能力和较快的收敛速度。

Fig.2 Convergence curves of Ackley function图2 Ackley 函数收敛曲线图

Fig.3 Convergence curves of Rastrigin function图3 Rastrigin 函数收敛曲线图

Fig.4 Convergence curves of Griewank function图4 Griewank 函数收敛曲线图

Fig.5 Convergence curves of Zakharov function图5 Zakharov 函数收敛曲线图

Fig.6 Convergence curves of Alpine function图6 Alpine函数收敛曲线图

Fig.7 Convergence curves of Exponential function图7 Exponential函数收敛曲线图

Fig.8 Convergence curves of Schaffer function图8 Schaffer函数收敛曲线图

Fig.9 Convergence curves of Schwefel 2.22图9 Schwefel 2.22 函数收敛曲线图

Fig.10 Convergence curves of Sphere function图10 Sphere函数收敛曲线图

Fig.11 Convergence curves of Schwefel 1.2 function图11 Schwefel 1.2 函数收敛曲线图

Fig.12 Convergence curves of Chung Reynolds function图12 Chung Reynolds函数收敛曲线图

Fig.13 Convergence curves of Sum squares function图13 Sum squares函数收敛曲线图

Fig.14 Convergence curves of Beale function图14 Beale函数收敛曲线图

Fig.15 Convergence curves of Booth function图15 Booth 函数收敛曲线图

Fig.16 Convergence curves of Goldstein&Price function图16 Goldstein&Price函数收敛曲线图

Fig.17 Convergence curves of Bohachevsky function图17 Bohachevsky 函数收敛曲线图

Fig.18 Convergence curves of Easom function图18 Easom 函数收敛曲线图

Fig.19 Convergence curves of Branin function图19 Branin 函数收敛曲线图

Fig.20 Convergence curves of Shubert function图20 Shubert函数收敛曲线图

3.4 三种策略下发现概率P 的比较分析

在布谷鸟搜索算法中发现概率P为重要的参数之一，为了比较三种策略下发现概率P的曲线变化，选取本文表1 中的f3(x)函数进行测试。f3(x)是典型的非线性多模态函数，搜索空间大并具有许多局部极小点。CS 算法、ACS 算法参数设置与表2 中DECS算法参数设置相同。

这里CS 算法发现概率P=0.25；ACS 算法发现概率Pa是典型性的自适应概率；DECS 算法发现概率P0是在典型的自适应概率Pa的基础上，引入种群分布熵的策略。

由图21 可知，CS 算法发现概率P=0.25 概率分布图为一条直线，在整个迭代过程中发现概率为一个固定值。由图22 可知，ACS 算法发现概率Pa概率分布图为一条抛物线，发现概率Pa随着迭代次数的增加而增加，在ACS 算法中迭代次数为200 次时，发现概率Pa已经达到0.416 6，不利于算法前期的种群多样性。DECS 算法发现概率P0概率分布图为一条不规则且跌宕起伏的曲线图。由式（8）可知发现概率P0的大小由自适应性Pa和空间种群分布位置分布信息共同决定。Si表明着种群分布情况，种群越分散Si越大，由式（10）可知惯性权重的变异算子Gi越小，使得P0越小，反之P0越大。例如由图23 可知，P0概率分布前200 次迭代中，概率在0.1～0.2 之间呈不规则分布，表明布谷鸟在解的子空间Ωj中位置信息比较分散且不断寻优。在第399 次迭代P0=0.363 8，400 次迭代P0=0.352 5，401 次迭代P0=0.385 8。概率P0由大到小，再由小到大，说明布谷鸟种群分布在解空间位置不断变化。位置信息在寻优过程中不断在变化影响着概率P0的大小。在DECS 算法后期636 次迭代到1 000 次迭代，发现概率P0概率分布为一条规则且光滑的曲线。表明种群分布集中在某个解的子空间Ωj内不断寻优。种群分布策略的引进有效提高了算法前期的种群多样性，同时也加强了算法后期的局部搜索能力。

Fig.21 Probability curve of P distribution of CS algorithm图21 CS 算法概率P 曲线分布图

Fig.22 Probability curve of Pa distribution of ACS algorithm图22 ACS 算法概率Pa 曲线分布图

Fig.23 Probability curve of P0distribution of DECS algorithm图23 DECS 算法概率P0曲线分布图

3.5 三种莱维飞行模式比较分析

在布谷鸟搜索算法中，由Levy(λ)～μ=t-λ可知，布谷鸟连续的位置变化形成了一个带有重尾分布的概率分布，使得布谷鸟飞行路径表现出了Levy 飞行的本质，即在寻优路径中频繁的短步长偶尔会出现长步长，使得CS 算法拥有更大的全局搜索能力，但是仍然存在全局搜索能力不足的缺陷。

本文提出的自适应双重莱维飞行机制主要分为两个阶段：搜索前中期和搜索中后期。由步长更新公式可知，该式描述莱维飞行是一个马尔科夫链，即下代的位置仅取决于当前位置信息。下一次位置是由当前位置Levy 飞行步长及步长因子ω共同决定的。由图1 步长因子ω变化曲线可知，DECS 算法前期拥有较小的步长因子，且Levy 飞行搜索偶尔出现的长步长，确保了算法前期每只布谷鸟在子空间Ω1,Ω2,…,Ωk中充分搜索。DECS 算法的中后期由子空间Ωk的搜索范围，扩大到整个解空间Ω的搜索范围，较大的步长因子确保了整个解空间Ω的充分搜索能力。随着迭代次数的增加步长因子的减小，DECS 算法后期的局部搜索能力增强。

为了验证自适应双重搜索Levy 飞行在全局搜索能力等方面的优势，从表1 中选取了4 个函数进行测试，f1(x)、f5(x)为复杂的多峰函数，拥有无数局部极小值和局部极大值，常导致算法在求解时陷入局部最优，可有效测试算法跳离局部极值的能力及全局收敛性能。f8(x)、f9(x)为单峰函数，由于它在全局最小值附近函数变化极为缓慢，因此被用来测试算法的收敛速度和寻优能力。CS-Ⅱ算法（自适应双重搜索Levy 飞行）是CS 算法仅采用引进新型步长因子策略；ASCSA-Ⅰ算法（自适应搜索Levy 飞行）是CS 算法仅采用自适应步长因子策略；CS 算法（标准的Levy 飞行）是标准的布谷鸟搜索算法。CS-Ⅱ算法、ASCSA-Ⅰ算法、CS 算法参数设置与表2 中DECS 算法参数设置相同。图24～图27 分别为f1(x)、f5(x)、f8(x)、f9(x) 在n=10 维测试情况下的函数收敛曲线图。表22 为CS-Ⅱ算法、ASCSA-Ⅰ算法、CS 算法在n=10 维情况下，对f1(x)、f5(x)、f8(x)、f9(x)函数测试并记录，平均值、最佳值、最差值及标准差测试结果的比较。

由表22 可知，CS-Ⅱ算法求解精度优于CS 算法，相比CS 算法f1(x)、f5(x)、f8(x)、f9(x) 在求解精度上分别提高了11、5、13、18 个数量级。CS-Ⅱ算法比ASCSA-Ⅰ算法在f1(x)、f5(x)求解精度上分别提高了8、2 个数量级，虽然在f8(x)、f9(x)求解精度上相差不多，但是在收敛速度上CS-Ⅱ算法优于ASCSA-Ⅰ算法。由图26、图27 可知CS-Ⅱ算法在100 次迭代收敛到全局最优，而ASCSA-Ⅰ算法在200 次迭代收敛到全局最优。由图24、图25 可知，CS 算法易陷入局部最优，而CS-Ⅱ算法在求解复杂的多峰且拥有无数的全局极小值的函数时，表现出更好的全局寻优性能，说明CS-Ⅱ算法比CS 算法更易跳出局部最优。由图24～图27 可知，CS-Ⅱ算法收敛速度优于ASCSA-Ⅰ算法、CS 算法。CS-Ⅱ算法在求解f1(x)、f5(x)多峰函数时，在300 次迭代内可收敛到全局最优，ASCSA-Ⅰ算法分别在500、650 次迭代收敛，CS 算法陷入局部最优；CS-Ⅱ算法在求解f8(x)、f9(x)单峰函数时均在100 次迭代内可收敛到全局最优，ASCSA-Ⅰ算法均在200 次迭代收敛到全局最优，CS 算法在求解f9(x)函数时400 次迭代收敛到全局最优，在求解f8(x)函数时1 000 次迭代未收敛。

Fig.24 Convergence curves of three Levy modes Ackley function图24 三种莱维模式Ackley 函数收敛曲线图

Fig.25 Convergence curves of three Levy modes Alpine function图25 三种莱维模式Alpine函数收敛曲线图

Fig.26 Convergence curves of three Levy modes Sphere function图26 三种莱维模式Sphere函数收敛曲线图

Fig.27 Convergence curves of three Levy modes Schwefel 2.22 function图27 三种莱维模式Schwefel 2.22 函数收敛曲线图

Table 22 Performance test results of three Levy modes表22 三种莱维模式的性能测试结果

3.6 三种改进策略的有效性分析

为了分析3 种改进策略对算法的性能影响，选取表1 中16 个函数进行测试，表23 测试结果为f1(x)～f5(x)、f7(x)～f9(x)、f12(x)函数，维数n=50；f13(x)～f19(x)函数，维数n=2；记录每次测试结果并计算平均值、最佳值、最差值、标准差；图28、图29 分别为5 种不同策略下，维数n=50 的f5(x)函数收敛图和维数n=2的f15(x)函数收敛图。将DECS 算法分别与CS-Ⅰ算法、CS-Ⅱ算法、CS-Ⅲ算法、CS 算法进行比较测试。这里CS 算法是基本的布谷鸟算法；CS-Ⅰ算法是CS算法仅采用在随机偏好游走的更新公式引入非线性对数递减的惯性权重策略；CS-Ⅱ算法是CS 算法仅采用引进新型步长因子策略；CS-Ⅲ算法是CS 算法仅采用在发现概率P中引进种群分布策略。CS-Ⅰ算法、CS-Ⅱ算法、CS-Ⅲ算法及CS 算法4 种算法参数设置与表2 中DECS 算法参数设置相同。

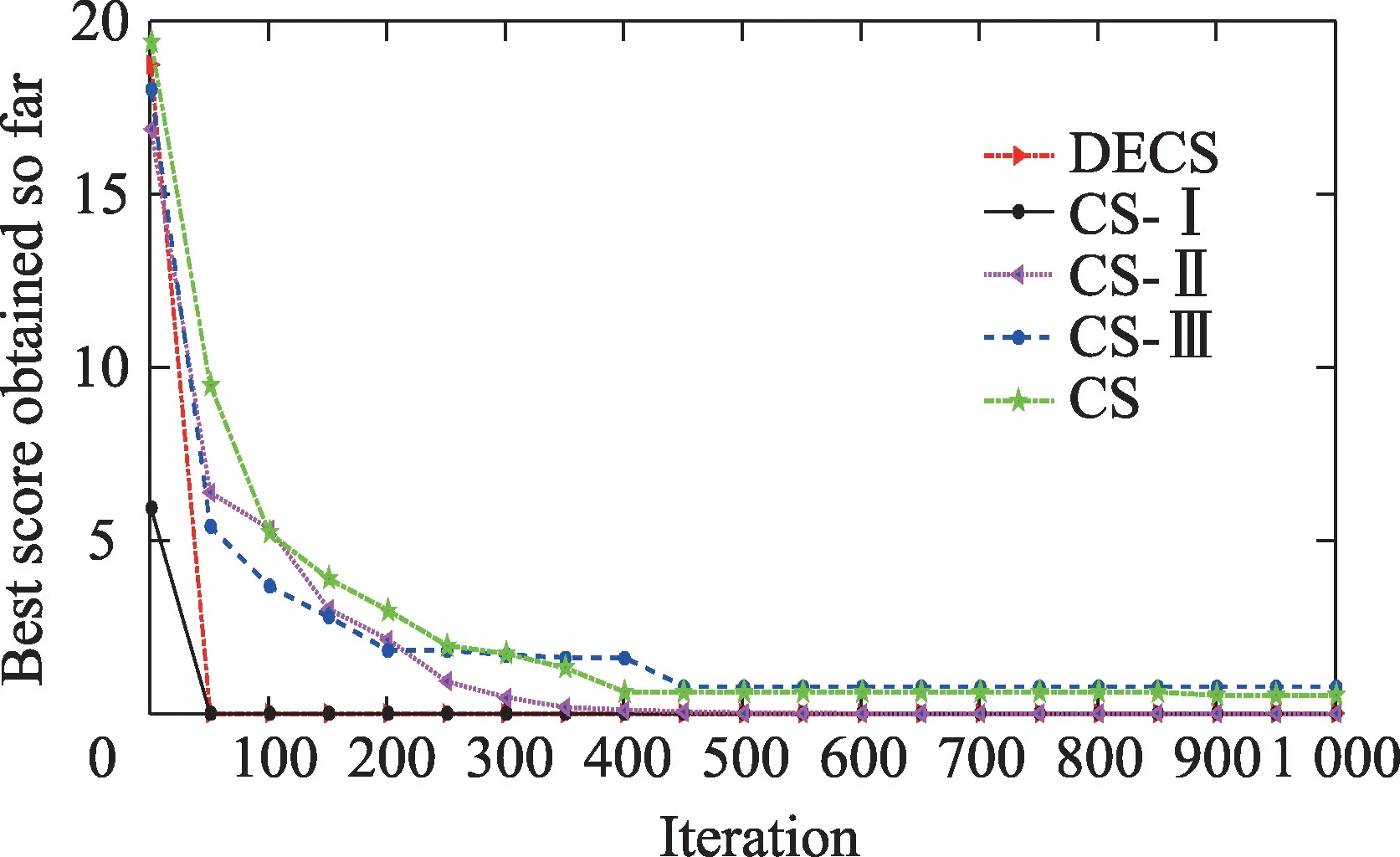
Fig.28 Convergence curve of Alpine function with different strategies图28 不同策略Alpine函数收敛曲线图

Fig.29 Convergence curve of Goldstein&Price function with different strategies图29 不同策略Goldstein&Price函数收敛曲线图

由表23 的比较结果可知，CS-Ⅰ算法在高维多峰函数、高维单峰函数上的寻优性能优于CS 算法、CS-Ⅱ算法、CS-Ⅲ算法。CS-Ⅰ算法求解f1(x)函数的精度相对于CS 算法提高了17 个数量级，f2(x)～f5(x)、f7(x)～f9(x)、f12(x)均可收敛到理论最优解。CS-Ⅱ算法在低维多峰函数、低维单峰函数上寻优性能优于CS-Ⅰ算法、CS-Ⅲ算法、CS 算法。f13(x)～f19(x)均可收敛到理论最优值。采用CS 算法在测试f13(x)、f16(x)～f17(x)函数时很容易陷入局部最优解，而CS-Ⅱ算法均可收敛于理论最优解。说明双重Levy 飞行搜索CS-Ⅱ算法比标准Levy 飞行搜索CS 算法更容易跳出局部最优解，有效克服了陷入局部最优的缺陷。由图28 可知，CS-Ⅰ算法在高维函数寻优精度和收敛速度上性能优于CS-Ⅱ算法、CS-Ⅲ算法、CS 算法。由图29 可知，CS-Ⅱ算法在低维函数的收敛速度上优于CS-Ⅰ算法、CS-Ⅲ算法、CS 算法。而CS-Ⅲ算法优于CS 算法，CS-Ⅲ算法在350 次迭代收敛到全局最优，CS 算法在600 次迭代收敛到全局最优，表明在概率P上引进种群分布熵策略，提高了CS 算法的收敛速度。

Table 23 Test comparison of five algorithms表23 5 种算法的测试比较

表23 （续）

DECS 算法采用了CS-Ⅰ算法、CS-Ⅱ算法、CS-Ⅲ算法中的策略，表现出了良好的寻优能力。f1(x)函数求解精度相对于CS 算法提高了17 个数量级，f2(x)～f5(x)、f7(x)～f9(x)、f12(x)～f19(x)函数均可收敛于理论最优值。对于高维多峰函数、高维单峰函数、低维多峰函数、低维单峰函数DECS 都表现出了良好的普适性。组合改进策略可以更加有效地提高算法的寻优性能。

3.7 DECS 算法跳出局部极值能力分析

基本的CS 算法的偏好游走中，下一代鸟窝位置更新是采用固定上一代位置为参考的更新方式，容易造成算法在迭代后期陷入局部最优解。因此本文提出了在偏好游走环节引入对数递减策略。DECS算法主要分为两个寻优阶段：迭代前期、迭代后期。由图1 可知，迭代前中期莱维飞行由于动态变化步长因子ω，已经将搜索精度缩小一个或多个数量级，因此偏好游走在迭代前期以较大的惯性权重κ保留上一代的位置信息，可以有效跳出子空间Ωj局部极

为了更好地验证DECS 算法的搜索效率及收敛性，本文设定了固定精度。从表1 中选取了9 个函数进行测试，对每个函数在固定精度下独立运行30次。记录每个函数在固定精度下的最小迭代次数、最大迭代次数、平均迭代次数、算法成功率、运行时间。测试结果如表24 所示。表24 中“最小迭代次数”为函数寻优独立运行30 次中达到预设精度值时的最小迭代次数；“最大迭代次数”为函数寻优独立运行30 次中达到预设精度值时的最大迭代次数；“平均迭代次数”为函数寻优独立运行30 次中达到固定精度值时所有运行次数的平均数，最大迭代次数设置为3 000 次，如果实验过程中迭代次数超过3 000，就认为寻优失败，其中没有达到预设精度的运行次数不算在内。“—”表示函数重复寻优过程中没有一次达到预设精度，“运行时间”为30 次函数寻优过程运行时间的平均数。算法成功率=达到精度的运行次数/总次数。

Table 24 Comparison of algorithm success rate and number of iterations表24 算法成功率和迭代次数比较

由表24 可知，本文提出的DECS 算法在9 个测试函数上进行的30 次独立运行实验，都达到了目标精度并且成功率均为100%。对于f3(x)、f4(x)、f5(x)、f7(x)复杂的多峰函数，在寻优精度固定的情况下，DECS算法的平均迭代次数明显小于ASCSA、CS、BA 和FPA 算法，且成功率都达到了100%，而对f3(x)函数FPA 算法的成功率只有83.3%，f5(x)函数CS 算法的成功率只有60%，充分说明了DECS 算法具有更好的搜索能力以及更高的收敛效率。f8(x)、f9(x)、f12(x)为单峰函数，测试函数的搜索效率和寻优能力。DECS 算法在平均迭代次数50 次以内，均达到了固定收敛精度，表现出了较优的收敛效率。面对二维的f15(x)、f19(x)多峰且具有多个极值点的函数，DECS 算法在平均迭代次数上优于ASCSA 算法，表明DECS算法有较强的跳出局部最优能力。从表24 第8 列运行时间可以看出，DECS 算法在时间效率上均高于ASCSA、CS、BA 和FPA 算法。

4 结束语

针对布谷鸟收搜索算法存在易陷入局部最优，后期收敛速度慢，求解精度不高等不足，分析基本布谷鸟的寻优过程与特性，提出了动态调整概率的双重布谷鸟搜索算法。该算法在发现概率P引入种群分布熵的概念，P不仅随着迭代次数的增加而变化，同时还随着布谷鸟分布的情况而变化，使得算法前期增加了种群的多样性且增强了全局搜索能力。布谷鸟寻优过程中引入了动态变化步长因子ω，使得算法前期在各自的子空间中进行Levy 飞行寻优机制，中后期再由整个解空间到局部精细搜索。有效改善了基本布谷鸟算法易陷入局部最优，收敛速度慢，求解精度低等缺点。通过19 个测试函数验证，DECS 算法的寻优能力、求解精度、收敛速度等方面均有较大幅度的提升。