粒子群优化算法在关联规则挖掘中的研究综述

钟倩漪，钱 谦，伏云发，冯 勇

昆明理工大学信息工程与自动化学院云南省计算机技术应用重点实验室，昆明650500

数据挖掘（database mining，DM）又称数据库中的知识发现（knowledge discovery in database，KDD），是从大量数据中提取出可信、新颖、有效并能被人理解的模式的高级处理过程[1]。关联规则挖掘（association rule mining，ARM）是一种寻找数据库中的频繁项或属性集之间相关性和因果关联的数据挖掘方法[2]，由Agrawal 等人[3]于1993 年针对购物篮问题首次提出，主要用于发现数据之间隐藏的关联关系。目前，关于关联规则挖掘的相关研究较为成熟，一般使用精确算法或智能算法对之进行求解，如Apriori 算法[3]、FP-growth（frequent pattern growth）算法[4]、Eclat算法[5]等都是典型的精确算法。精确算法首先从事务集合中找出频繁项集，然后从频繁项集中挖掘出强关联规则，但在处理大量数据候选项集和复杂数据时会带来严重的时间、存储开销[6]，且大部分算法需要人为设置支持度和置信度的阈值，导致结果易产生冗余规则及忽略重要规则。因此，部分学者转而研究智能算法在关联规则挖掘中的应用。Minaei-Bidgoli等人[7]提出了一种基于粗糙模式的多目标遗传算法进行数值关联规则挖掘，该方法使用由上限和下限间隔定义的粗略值来表示一个范围或一组值，同时使用帕累托最优思想解决多目标优化问题，有效提高了算法性能。Thangavel等人[8]提出了TACO-Miner（threshold ant colony optimization miner）方法，该方法是一种用于挖掘分类关联规则的改进蚁群优化算法，可以挖掘出具有更高预测精度及更为简单的分类规则。Wang 等人[9]提出了一种基于粒子群优化算法的关联规则挖掘方法，在分类数据上与传统Antminer算法相比具有更高的预测精度和更精简的规则集合。以上研究表明，智能算法具有良好的可扩展性，与一些精确算法相比执行速度较快，挖掘结果更具有价值。其中，粒子群优化算法因其实现简单、收敛速度快、搜索能力强等优点受到诸多学者关注，被广泛应用于关联规则挖掘领域，并取得了大量具有重要意义的研究成果。

现有研究表明，使用粒子群优化算法进行关联规则挖掘较遗传算法有更好的运算效率，能够生成更有效的规则[9]。目前还没有专门针对粒子群优化算法解决关联规则挖掘问题进行介绍的相关综述，因此，为方便相关研究者对该领域有更为清晰的理解，本文概述了粒子群优化算法在关联规则挖掘中的相关研究和应用，并总结了未来的潜在研究方向。

1 相关概念及原理

1.1 粒子群优化算法基本原理

粒子群优化（particle swarm optimization，PSO）算法[10]是一种基于群体的随机搜索算法，由Kennedy 和Eberhart 于1995 年提出，其思想主要源于鸟类和鱼类群体的社会行为。标准PSO（standard particle swarm optimization，SPSO）算法[11]中，每一个粒子表示问题的一个候选解，具有速度和位置两个属性，粒子通过个体最优解（Pbesti）和全局最优解（Gbest）不断调整自身的飞行方向和速度，从而改进候选解。假设第t次迭代时粒子群p(t)中包含N个粒子，第i个粒子在K维解空间中的位置向量表示为=(xi1,xi2,…,xiK)，速度向量表示为=(vi1,vi2,…,viK)，Pbesti表示为Pi=(Pi1,Pi2,…,PiK)，Gbest表示为G=(G1,G2,…,GK)。第i个粒子在下一次迭代中的速度及位置更新公式如下：

其中，ω为惯性权重，ω∈[0,1]；c1为自我学习因子，c2为社会学习因子，一般情况下c1=c2=2；r1、r2为分布在[0,1]区间上的随机数。

1.2 关联规则基本概念

在关联规则问题中，设项集I={i1,i2,…,ik}为k个不同数据项的集合，k为数据项的长度，长度为k的数据项称为k-项集，数据集D={t1,t2,…,tn}为n个不同事务的集合，且tn≠∅，每个事务tn对应I中的一个子集，即tn⊆I。设X⊆I，Y⊆I，且X⋂Y=∅，则X→Y为一条关联规则，其中X被称为规则的前件，Y被称为规则的后件，X→Y的支持度和置信度定义如下：

定义1（支持度）关联规则X→Y的支持度是指包含X和Y的事务占所有事务的比例，即事务X和Y同时出现在数据集D中的概率。

定义2（置信度）关联规则X→Y的置信度是指事务X包含事务Y的比例，即事务Y出现在事务X中的概率。

若support(X→Y)和confidence(X→Y)均满足最小支持度和置信度阈值，则认为关联规则X→Y为一条强关联规则。

关联规则挖掘最早用于分析超市商品的购买情况，其中，沃尔玛超市的“尿布和啤酒”是最为经典的例子，其商品交易的数据示例如表1 所示。

Table 1 Supermarket commodity sales data表1 超市商品销售数据

表1 中包含商品面包、牛奶、尿布、啤酒、鸡蛋、可乐，可具体表示为i1、i2、i3、i4、i5、i6，即项集I=(i1,i2,…,i6)。表中共有5 个事务，其中同时包含尿布和啤酒的事务总数为3 个，则规则i3→i4的支持度计算如下：

结合表1 中的数据，包含尿布的事务总数为4个，则规则i3→i4的置信度计算如下：

2 PSO 算法的研究现状

传统PSO 算法自提出以来，众多学者从参数、收敛性、运动轨迹、拓扑结构等角度进行研究，并针对其不足进行改进，以提高算法性能。2002 年Clerc 和Kennedy[12]提出带有收缩因子χ的PSO 算法，避免粒子速度和位置增长到无穷大时发生的“爆炸”或“随机游走”情况，在确保算法收敛的同时扩大粒子的探索范围，其速度更新公式如下所示：

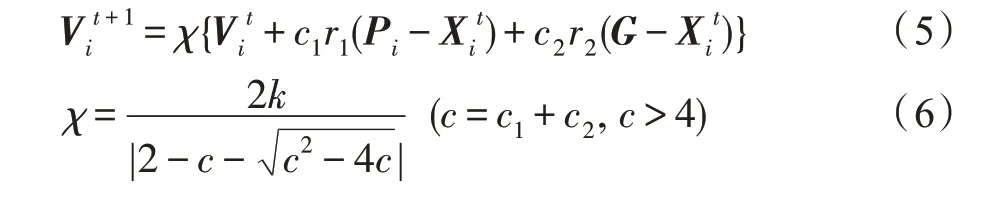
其中，k为分布在(0,1]区间上的随机数，一般情况下k=1，c1=c2=2.05，χ=0.729 8。

运动轨迹的调整在一定程度上影响整个粒子群的搜索趋势，一些学者将变异算子、量子力学及混沌思想引入PSO 算法，如2003 年Higashi和Iba[13]将高斯分布、变异算子与PSO 算法相结合，通过高斯分布的概率改变粒子的轨迹，改进后的粒子位置更新公式如下所示：其中，变异概率σ由1.0 线性递减至0，在算法前期粒子进行广泛搜索，中后期进行加速搜索，因此，引入高斯变异机制的算法在单峰和多峰函数上的测试结果均优于GA（genetic algorithm）及PSO 算法。2004年，Ratnaweera 等人[14]同样将变异算子引入到PSO 算法中以保证群体多样性，Juang[15]将精英选择、交叉、变异算子结合在一起，对适应度排名前50%的粒子进行交叉、变异操作后生成剩余粒子，实验结果表明改进后的算法搜索精度更高。Sun 等人[16]受量子力学启发提出量子粒子群优化（quantum-behaved particle swarm optimization，QPSO）算法，有效改进了PSO 算法中易陷入局部最优的缺陷。该算法参考量子不确定性原理，每个量子空间中的粒子速度和位置不能同时确定，即可对解空间中的任意位置进行搜索，加强了算法的寻优能力。QPSO 算法的位置更新公式如下所示：

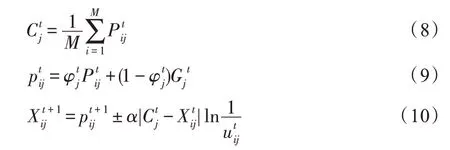
其中，μ为控制参量，μ∈[0,4]。

迄今为止，针对PSO 算法定义了许多不同的拓扑结构，包括星型拓扑（star topology）、环型拓扑（ring topology）、轮式拓扑（wheel topology）及金字塔型拓扑（pyramid topology）结构等，每种结构存在不同优缺点[18-19]。拓扑结构实际上决定了粒子间的关联方式，如SPSO 算法属于全局最优算法，该算法采用星型拓扑结构，每个粒子均与全局最优粒子相关联。除了众所周知的拓扑结构，一些学者提出了其他拓扑结构，如：Janson 和Middendorf[20]于2005 年提出了基于树型拓扑的分层粒子群优化（hierarchical particle swarm optimization，HPSO）算法；Zhang 和Yi[21]于2011年提出了基于自适应拓扑的无标度全信息粒子群优化（scale-free fully informed particle swarm optimization，SFIPSO）算法；Jiang 等人[22]于2013 年提出了一种基于年龄组拓扑的粒子群优化（particle swarm optimization with age-group topology，PSOAG）算法。

3 PSO 算法在关联规则挖掘中的研究

3.1 数据转换

数据库中的数据类型一般分为连续型和离散型，连续型数据可直接存储为实数格式，而离散型数据需对数据进行二进制转换。在关联规则挖掘中，大部分数据为离散型，需将每条事务数据记录和存储为0 或1[23]，这种处理方式能加速数据库的扫描操作，且便于计算置信度和支持度。根据表1所描述的商品交易数据集实例，对其数据的二进制变换如图1所示。

图1 中，数据集包含5 条交易记录T1至T5，共有6个不同项即6 个不同商品，每条交易记录包含一定数量的商品，若商品存在于交易记录中则存储为1，若不存在则为0。以事务T1为例，在这条交易记录中仅购买商品I1和I2，因此二进制变换后的交易数据为110000。

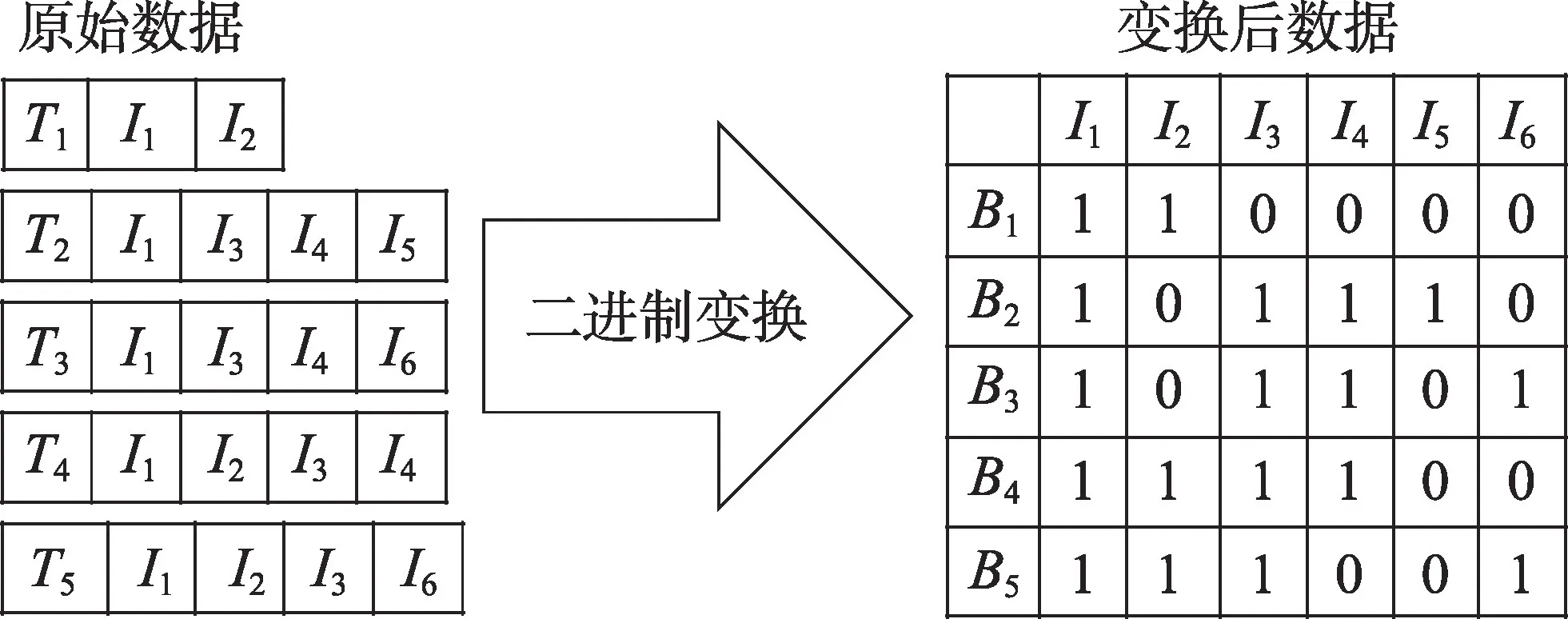
Fig.1 Binary transformation of data图1 数据的二进制变换

传统PSO 算法一般只适用于解决连续型数据的关联规则挖掘，针对离散型数据的关联规则挖掘需使用改进后的PSO 算法。Kennedy 和Eberhart[24]于1997 年对PSO 算法进行改进，提出了二进制粒子群优化（binary particle swarm optimization，BPSO）算法，该算法用于解决离散或组合优化问题。为了将粒子限制在{0,1}空间内，BPSO 算法的位置更新方式不同于传统PSO 算法，该算法使用sigmoid 函数作为变换函数，将粒子速度转换为[0,1]区间上的概率，通过概率决定粒子的位置为0 或1。二进制粒子位置更新的公式如下所示：

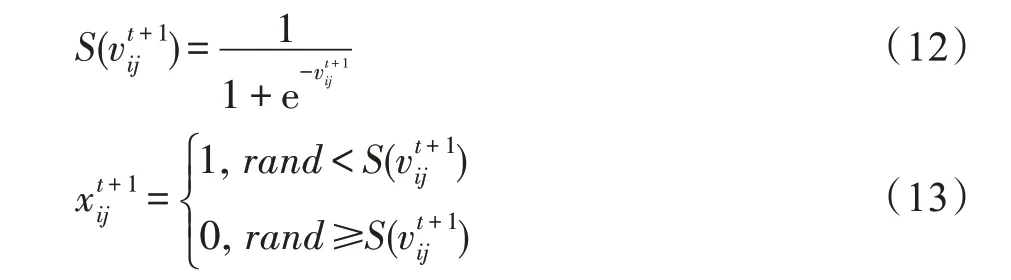
其中，rand为分布在[0,1]区间上的随机数。

3.2 编码方式

PSO 算法进行关联规则挖掘时主要采用两种方法对规则进行编码：第一种方法为匹兹堡方法（Pittsburgh approach），该方法关注所有规则的特征，每个粒子表示为一组规则，需对数据中包含的所有规则进行编码，因此该方法计算量较大、可移植性差[25]，比较适用于解决分类规则挖掘问题；第二种方法为密西根方法（Michigan approach），该方法关注单条规则的质量，每个粒子表示为一条规则，只需对数据中的部分规则进行编码，与匹兹堡方法相比，编码方式简单直接，具有更短的规则语法，在计算上更为高效[26]。基于上述原因，大部分涉及PSO 算法解决关联规则挖掘问题的文献中均使用密西根方法，能更为有效地挖掘出高质量预测规则及罕见规则。以密西根方法为例，假设数据库中存在N个项目，每个项目包含两个部分VN1和VN2，VN1的取值表示该项目是否出现在规则中，VN2的取值表示该项目为规则前件或规则后件，根据图1 中的商品交易数据集随机生成的一条规则编码如图2 所示。

Fig.2 Encoding with Michigan approach图2 使用密西根方法进行编码

图2 中，I1的编码为11，表示该项目存在于规则中且为规则前件，I2的编码为10，表示该项目为规则后件，因此，该编码表示为一条I1→I2的关联规则。

3.3 规则评估

在经典关联规则挖掘算法中，一般通过支持度和置信度衡量关联规则的好坏，但高支持度的项会直接产生高置信度的规则，与项之间的关联关系无关，仅考虑支持度和置信度容易挖掘出无效规则。因此随着相关研究的深入，一些用于衡量规则质量的新标准被提出，包括兴趣度、理解度、相似度等。

3.3.1 兴趣度

文献[27]和文献[28]指出大部分具有高置信度的规则并不会让人感兴趣，此类规则是重复且无意义的规则，如购物篮问题中挖掘出的“牙膏→牙刷”规则，此类规则容易被用户预测，是无趣的规则，而关联规则挖掘的主要目的是为了获取具有意外及隐含特性的规则，此类规则的支持度或置信度普遍较低，因此，仅考虑支持度和置信度两个标准难以针对用户的需求找到其真正感兴趣的规则。李呈林等人[29]引入基于差异思想的兴趣度标准，从规则的置信度与后件的支持度差异定义兴趣度，帮助用户在众多规则中选择更有意义的关联规则，节省大量分析规则的时间，其计算公式如下所示：

式（14）中，max{fconf(X→Y),fsup(Y)}表示标准化因子，其作用为将兴趣度的绝对值限制在[0,1]范围内，fconf(X→Y)-fsup(Y)表示为后件Y在前件X影响下发生的概率与自身发生概率的差异。规则X→Y的置信度与后件Y的支持度差距越大，表明该规则越新奇，即X→Y大概率为一条包含重要信息的隐含关联规则，更容易让人感兴趣。

基于差异思想的兴趣度标准主要是为了避免具有高支持度的后件Y直接产生高置信度的规则这一问题，从而消除用户不感兴趣、甚至错误的规则，但该标准应用领域有限，较难适用于分类数据问题。由于分类数据集要将规则后件中的每个属性进行划分，即后件部分可能包含比较多的项，使用式（14）计算发现此类规则都为低兴趣度规则。因此，文献[30]提出基于概率思想的兴趣度标准，文献[31-34]引入该兴趣度标准对规则进行评估，其计算公式如下所示：

式（15）使用规则前件和后件的置信度及支持度去评估兴趣度，主要分为三部分：第一部分表示基于规则前件的置信度；第二部分表示基于规则后件的置信度；第三部分表示可能无法根据整个数据集生成规则的概率。该评估标准对规则前件X与后件Y的置信度及规则的支持度进行综合度量，由于低支持度及高置信度规则容易产生高兴趣度规则，因此能挖掘出一些具有实际应用价值且难以被用户预测的关联规则。

3.3.2 理解度

支持度和置信度标准依据规则在整个数据库中的出现次数来评估其质量，若规则出现的次数越多则认为这是一条有效规则，但仅考虑这两个标准生成的规则可能包含大量属性，难以被用户理解[35]，从而此类规则被使用的概率非常低。基于上述原因，理解度标准被提出且广泛应用于规则的衡量之中，该标准从规则的简洁性和包含的信息量进行综合度量，规则越简洁、信息量越大，则越容易被人理解。文献[31-34，36]引入一种使用较多的理解度标准，其计算公式如下所示：

式（16）中，|Y|、|X∪Y|分别表示规则后件和总的规则中包含的属性数量，ln 函数用于标准化函数值的范围，若规则包含的总属性数量较少且规则后件包含的属性较多，则该评估标准能够挖掘出易被理解的规则。

3.3.3 相似度

实际应用中，使用PSO 算法或其他智能算法可以产生一组具有高适应度值的关联规则集合，但其中部分规则存在相似度过高的情况[37]。相似的规则容易造成规则库的冗余，不利于用户决策，因此相似度标准被提出且用于衡量规则的有效性。若一条规则的前件和后件包含另一条规则的前件和后件，则两条规则存在相似关系，例如存在关联规则集合D={AR1,AR2,…,ARn}，关联规则AR1:X→Y，AR2:X→(Y,Z)，AR3:Y→Z，则AR1与AR2存在相似关系，AR1与AR3不存在相似关系。Kou等人[36]引入一种衡量规则的相似度标准，其计算公式如下所示：

式（17）中，support(ARi,ARj)为ARi及ARj包含的事务在数据库中出现的次数，support(ARi)为ARi包含的事务在数据库出现的次数，若规则ARi与ARj不存在相似关系，则Simi[i,j]=0。该评估标准综合考虑规则ARi及ARj支持度概率分布的相似程度，对挖掘出的相似规则进行筛选，能够挖掘出更为有效的规则。

上述文献均考虑多种评估标准对规则质量进行衡量，从而避免仅考虑支持度和置信度所造成的缺陷。

3.4 PSO 算法与其他关联规则挖掘算法对比

本文选取了5 个在关联规则挖掘领域中被广泛应用的算法与PSO 算法进行对比，结果如表2 所示。

关联规则挖掘算法可大致分为精确算法和智能算法两类[38]，其最大不同之处在于精确算法需要获取频繁项集，而智能算法可以忽略该步骤直接获取关联规则，且能生成包含不同项集长度的规则。

精确算法包含Apriori算法、FP-growth算法、Eclat算法等。Apriori 算法作为经典关联规则挖掘算法，其核心思想是通过候选集逐层搜索生成频繁项集，有效降低对非频繁项的扫描时间。假设数据集中包含n个项目，项集长度为k，则Apriori 算法的时间复杂度为O(2n)+O(2k)，在运行过程中候选集数量呈指数形式增长，需要消耗大量内存和运算时间。同时，随着数据维度和数量的增大，该算法容易产生大量候选集，对数据的重复扫描次数过多，特别是在产生的频繁项集过大时，算法运行时间显著增加。因此，Apriori 算法适用于频繁项集小的数据，即小规模稀疏数据的关联规则挖掘。FP-growth 算法和Eclat 算法分别使用不同挖掘方法对Apriori 算法进行改进。FP-growth 算法使用模式增长挖掘方法，提出一种FPtree 结构对数据高度压缩，与Apriori 算法相比无需产生候选集，直接通过FP-tree 挖掘频繁项集。文献[4]表明，当生成的FP-tree 足够小或路径重叠较多时，在算法的运行效率上，FP-growth 算法远优于Apriori 算法，但当数据集规模大、维度高时，递归构造FP-tree的子节点过多，产生大量内存开销，导致算法效率大幅度下降。因此，FP-growth 算法适用于低维布尔关联规则挖掘。Eclat 算法使用深度优先挖掘方法，与FP-growth 和Apriori 算法不同，该算法将数据转换为垂直格式，只需扫描一次数据库，极大地降低了I/O消耗，运行效率较高。但垂直数据格式对于内存的依赖较大，在大规模数据集中，项目出现的频率变高，构建的频繁项集过大，处理交集运算需要消耗大量内存，从而导致算法运行效率降低。

Table 2 Comparison of association rule mining algorithms表2 关联规则挖掘算法比较

智能算法包含遗传算法、蚁群优化算法、粒子群优化算法等，此类算法主要是对数据集D中的部分数据进行操作，无需扫描全体事务，能有效减少数据的读取时间[39]。遗传算法[40]（GA）通过种群个体间的选择、交叉及变异操作逐步获取最优解，具有良好的全局搜索能力，寻优精度较高，但个体没有记忆，遗传操作盲目无方向，所需收敛时间长[41]。在处理高维数据时，该算法编码后的染色体规模庞大，因此交叉及变异等操作需要大量I/O 消耗，导致算法的运行效率低，不易收敛。蚁群优化（ant colony optimization，ACO）算法[42]受蚁群觅食行为的启发，最初被应用于求解旅行商问题，具有良好的鲁棒性和全局搜索能力。蚂蚁系统使用信息素决定移动方向，只需扫描一次数据集[43]，但在分配周期中需消耗大量时间用于解的构造，搜索时间过长。当处理的数据规模过大时，该算法迭代次数较多、效率较低，容易发生停滞现象，存在陷入局部最优的可能。粒子群优化算法易于实现、收敛速度较快，文献[44]表明该算法在较大规模数据中的关联规则挖掘效率高于GA。但对于高维数据，该算法缺少类似GA 中的交叉、变异操作，搜索空间有限，粒子不能很好地处理探索（全局搜索）和开发（局部搜索）之间的关系，容易收敛到局部最优解。

4 改进PSO 算法在关联规则挖掘中的研究

4.1 基于参数的改进

使用智能算法寻找到问题中最优或近似最优解的概率很大程度上取决于参数的选取[45]，同样，PSO算法中参数的设置对其性能产生很大影响，设置合适的参数值能优化算法的性能。PSO 算法包含三个重要参数，分别为惯性权重ω、自我学习因子c1和社会学习因子c2，c1和c2为加速度参数，通常为两个常数。ω控制粒子历史速度对新速度的影响，c1和c2用于保持群体的多样性，c2用于增加算法收敛到全局最优的概率。其中，ω是决定PSO 算法收敛的关键，ω越大，算法的全局搜索能力越强，但可能会在最优解附近发生震荡，导致算法无法收敛；ω越小，算法的局部搜索能力越强，但粒子对解空间的探索能力较弱，容易陷入局部最优。因此，合适的惯性权重能平衡粒子的局部搜索和全局搜索能力，合适的自我学习因子和社会学习因子能降低算法陷入局部最优解的概率。

Mangat 等人[46]提出一种基于动态自适应PSO 算法的关联规则挖掘分类器，即动态自适应联想分类器，该分类器试图在保持规则集合较小的同时最大化预测精度，使用自适应参数、区域动态重建和速度更新等改进，为粒子提供每个维度的最佳值。其中，PSO 算法使用基于平均理想速度概念对ω进行非线性调整，当粒子速度过大时，使用较小的ω；当粒子速度过小时，使用较大ω。同时，c1线性减少，c2线性增加，以上改进避免了算法过早收敛及陷入局部最优，平衡了粒子对解空间的探索和开发。关联规则的挖掘依赖于数据集中的项目和它们之间的关系，增加或降低参数值对算法性能的提升有限，因此，Indira等人[47]考虑数据依赖的自适应策略对PSO 算法进行改进，该算法根据数据集和生成的适应度值设置参数，通过欧几里德距离计算粒子之间的相似度，使用进化估计因子e和适应度对粒子状态进行估计，ω、c1和c2均使用自适应方式，ω基于适应度的变化动态调整，避免粒子陷入局部最优，整体呈线性下降，在收敛后期取值经常在0.461 左右波动。在粒子的探索前期和开发后期，c1值增加，c2值减少，允许粒子探索尽可能多的最佳区域；在粒子的收敛后期，c1和c2值均进行小幅度增加，帮助粒子尽可能寻找到全局最优解，加快算法的收敛。实验结果表明自适应PSO 算法在五个UCI（University of California Irvine）数据集上能挖掘出精度更高、数量更多的关联规则，但进化因子和参数自适应机制增加了算法的复杂度，与PSO 算法相比执行时间更长，且改进后的算法主要是与PSO 算法、SAPSO（self adaptive PSO）算法、ACO 算法进行对比，缺乏与精确算法的比较。

PSO 算法中的随机数参数r1、r2用于增加粒子飞行时的随机性，该参数的调整同样也能影响算法的性能。Alatas 等人[48]引入多目标混沌PSO 算法作为一种搜索策略来挖掘数据集中的分类规则，混沌映射的遍历性能加快算法的全局收敛，该算法中随机数r1、r2使用Zaslavskii 混沌映射[49]公式生成的序列进行替换，其公式如下所示：

一般情况下v=400，r=3，a=12，Yn+1∈[-1.051 2,1.051 2]，Xn+1∈[0,1]，此时变量X表现出良好的动态混沌性。Zaslavskii 映射产生的序列与传统Logistic 映射相比分布更为均匀，确保算法可以搜索到整个解空间，有助于粒子跳出局部最优解从而提高算法的全局搜索能力。但在大空间、多变量问题的优化搜索上，Zaslavskii映射的调用会增加PSO 算法的运行时间。

4.2 基于变异机制的改进

变异机制来源于自然选择中发生的基因突变，即生物染色体的基因在遗传过程中有一定概率发生改变，好的变异结果能增加种群的多样性。因此，针对传统PSO 算法的相关缺陷，变异机制的引入能增加算法的全局搜索能力，避免算法过快“早熟”。文献[50]引入变异算子，在PSO 算法的初始化阶段随机选择粒子进行变异操作，更新粒子的位置，避免其陷入局部最优的可能，然后使用改进后的PSO 算法对关联规则进行优化，能够挖掘出更为有效的规则。

普通变异算子对满足一定条件的粒子进行单次变异[51]，仅拓展了有限的搜索空间，因此王飞等人[52]提出一种多变异粒子群优化（multi-mutation PSO，MmPSO）算法，该算法将多变异算子与粒子群优化算法结合，通过设置多个维度的变异概率，对较差粒子进行多次单维变异和一次多维随机变异，从而提高粒子跳出局部最优解的几率，避免粒子由于收敛到局部最优而导致粒子群萎缩的情况，实验结果表明改进后的算法一定程度上提高了关联规则挖掘的准确率，但实验数据中包含的样本数量较少，且缺乏单独对多变异算子有效性的相关验证。文献[39]同样引入多变异算子，将其与粒子迁移策略结合提出MsPMmPSO（multi-swarm parallel MmPSO）算法，增加粒子种群的多样性，同时帮助粒子跳出局部最优解。

吴嵘等人[53]提出一种基于改进量子粒子群优化（improved QPSO，IQPSO）算法的关联规则挖掘方法，将数据实例以量子比特形式表示，构建一个基于QPSO 算法的关联规则挖掘基础框架，算法在迭代后期的角度变化幅度越来越小，有很大几率陷入局部最优。当算法后期量子个体最佳角度几乎没有改变时，引入变异算子，选择一些量子进行变异操作，把粒子与全局最优角度的距离作为变异概率，将远离最优角度的量子进行大概率变异，提高算法的全局搜索能力。

文献[54]指出基于PSO 算法的关联规则挖掘的最大缺点是用户必须指定生成最佳规则的数量，以及该算法在迭代次数过多情况下的时间复杂度高于Apriori 算法，处理大型数据集时效率较慢。基于上述考虑，Tahyudin 等人[32]将PSO 算法和柯西分布相结合求解数值关联规则挖掘问题，利用柯西变异进行跳跃搜索获得全局最优解，避免算法陷入局部最优，扩展粒子的搜索空间及增强粒子的进化能力。柯西变异策略能帮助粒子在大邻域内寻找其最优解，使算法具有鲁棒性，因此也适用于大型数据集的关联规则挖掘。大部分变异粒子围绕柯西分布中心进行分散，虽然减缓了粒子向局部最优位置聚集的趋势，但不能完全避免其陷入局部最优。

4.3 混合PSO 算法

PSO 算法与其他优化算法相结合可以充分发挥不同算法的优点，弥补各自算法的不足。混合PSO 算法主要分为三种类型：第一类将PSO 算法与精确算法进行混合；第二类将PSO 算法与其他智能算法进行混合；第三类将PSO 算法与神经网络进行混合。

4.3.1 混合精确算法

PSO 算法能有效优化数据，因此被应用于优化精确算法中的阈值或挖掘出的规则。曾本冲等人[55]提出一种改进PSO-Apriori 算法，使用PSO 算法优化Apriori 算法的支持度和置信度阈值，避免阈值需人为设置且不同数据需设置不同阈值的缺陷，PSO 算法的适应度函数为支持度和置信度的加权和，同时，该算法对优化后的多值属性关联规则进行改进，即在Apriori 算法的连接步骤中加入对特定维度的判断，能够挖掘出更为有效的关联规则。经典Apriori 算法使用逐层迭代的方式通过低维频繁项集得到高维频繁项集，在执行过程中需要频繁扫描数据库[56]，因此在挖掘大量数据中的关联规则时运行效率过低，陈建国[57]将PSO 算法与改进Apriori 算法结合用于处理大型数据集的关联规则挖掘，首先引入K-均值聚类思想，使用PSO 算法对大型数据库进行优化划分，形成多个子数据库，再在子数据库基础上采用改进后的Apriori 算法进行局部挖掘，最后合并各个局部频繁项集生成关联规则，从而解决海量数据挖掘的时间和空间复杂度过高的难点。虽然PSO 算法与Apriori 算法按先后顺序进行寻优，前期PSO 算法提高了运行效率，但算法精度仍有较大的提升空间。

FP-growth 算法使用分治策略构建频繁模式树（FP-tree）后进行频繁项集挖掘，与Apriori 算法相比挖掘效率更高。因此，越来越多的学者将PSO 算法与FP-growth 算法混合，如Mishra 等人[58]将PSO 算法与FP-growth 算法进行结合用于处理模糊频繁项集挖掘问题。首先使用FP-growth 算法构建模糊FPtree 挖掘出频繁项集，之后将PSO 算法应用于挖掘出的频繁项集，使用均方冗余（mean squared residue，MSR）分值作为适应度函数进行优化。实验结果表明，基于PSO 算法的模糊FP-growth 算法能挖掘出数量更多、结果更好的频繁项集，且运行效率较高。之后，考虑到PSO 算法容易早熟收敛，Mishra 等人[59]在之前研究基础上又引入了CLPSO（comprehensive learning PSO）算法[60]，该算法使用一种综合学习策略，利用所有粒子的个体最优位置更新粒子的速度，保持粒子群体的多样性，防止算法过早收敛。CLPSO 算法对模糊FP-growth 算法生成的频繁项集进行优化，生成的最佳频繁项具有较低的MSR 分值，优于标准PSO 算法。

Eclat 算法是一种频繁项集挖掘算法，与Apriori算法及FP-growth 算法相比，该算法无需重复扫描数据库，提高了规则的挖掘效率。Sathya 等人[61]提出一种IEPSO-ARM（integrated Eclat and PSO based ARM）算法进行高效关联规则挖掘，该算法将Eclat 算法挖掘出的规则作为PSO 算法的部分初始化粒子，随机初始化剩余的粒子，粒子的适应度函数用于衡量规则的有效性，因此，通过PSO 算法的优化能获得更为有效的规则。之后利用垂直布局格式来优化基于相关性度量生成的规则，即规则不仅基于相关性度量生成，同时基于相关性度量的强度生成。

4.3.2 混合智能算法

针对使用单一PSO 算法在解决问题时具有的收敛精度不足、局部搜索能力差等缺点[62]，文献[63]提出一种混合遗传粒子群优化（hybrid GA/PSO，GPSO）算法，将GA 与PSO 算法在同一个群体上并行运行，保证PSO 和GA 在互不影响的情况下共同迭代寻优，在迭代前期充分利用GA 的随机性扩大探索范围，迭代后期利用PSO 算法的快速收敛能力，实现算法探索与开发之间的平衡。虽然GPSO 算法较PSO 算法消耗时间更多，但挖掘出的关联规则更为精准。然而GPSO 算法仅考虑支持度和置信度两个指标，不能挖掘出更为有效的高质量规则，因此Agarwal 等人[64]提出一种NSGA-II-MPSO（nondominated sorting genetic algorithm II and multi-objective PSO）算法对购物篮数据进行多目标关联规则挖掘，该算法将带精英策略的非支配排序的遗传算法[65]（nondominated sorting genetic algorithm II，NSGA-II）与多目标粒子群优化（multiobjective PSO，MOPSO）算法[66]进行混合，平衡对规则的探索和开发。该算法将初始化中适应度较高的一半规则视为染色体，使用NSGA-II 进行优化，另外一半规则被视为粒子群体，使用快速收敛MOPSO算法进行增强，将使用不同算法的输出结果重新组合，生成新的群体进行下一代传播。NSGA-II 的精英策略保留了全局最优解，且通过交叉和变异操作能产生带有新染色体的子代，将遗传算法用于适应度较高的个体避免算法陷入早熟收敛[63]，而MOPSO算法借助个体反馈机制和基本的群体交互作用，增强适应度较低的个体，帮助其寻找到最优解，改进后的算法收敛速度更快、算法性能更高，但实验只与单目标算法进行了对比，且未考虑包含负相关项的规则。Zhou 等人[67]提出A_PSOGSA（adaptive PSO gravitational search algorithm）用于解决关联规则挖掘问题，该算法混合了自适应粒子群优化[68]（adaptive PSO，APSO）算法、GA 及引力搜索算法[69]（gravitational search algorithm，GSA）。GSA 具有较好的全局寻优能力，通过粒子的惯性质量、在每个方向的引力、加速度等信息，增加粒子群的记忆能力和粒子间的交流，加强粒子间的相互作用。混合后算法在每次迭代更新中考虑所有粒子的适应度，任何粒子都可以感知全局最优解，并与之保持接近，因此能提高算法的局部搜索能力。同时，该算法保存每次迭代后产生的全局最优解，有利于关联规则挖掘。最后，该算法在进化过程中利用种群分布信息动态控制加速系数，能更好地平衡全局和局部搜索能力。佘雅莉等人[70]混合了PSO 算法与ACO 算法对危险源原因进行关联规则挖掘，先使用PSO 算法挖掘出数据集中的频繁项集，从而确定ACO 算法的初始信息素浓度，避免蚁群运动的盲目性，同时增加算法的搜索能力。当蚂蚁完成一次搜索后，对本次迭代中的最优频繁项集中的点所构成的边进行信息素更新，直至挖掘出最大频繁项集，生成质量较好的强关联规则，实验结果表明使用混合后的算法更容易对危险源原因进行分析。

4.3.3 混合神经网络

人工神经网络（artificial neural network，ANN）具有自学习、自组织、自适应和非线性动态处理等特性，PSO 算法与ANN 的结合能更有效解决实际问题。Dhanalaxmi 等人[71]使用分类关联规则挖掘方法对软件缺陷进行分类，避免软件缺陷的产生，而软件缺陷数量越少则表明软件质量越高。该方法在挖掘关联规则之前，使用自适应PSO 算法对规则进行优化，提供更具体的聚类结果，避免挖掘到大量无效规则。之后，使用前馈反向传播神经网络（feed forward back propagation neural network，FFBNN）分类器对确定的实际缺陷进行分类，改进后的分类关联规则挖掘方法精确度达到99.5%。

PSO算法也适用于优化人工神经网络的权值，Ma等人[72]使用加权模糊神经网络（weighted fuzzy neural network，WFNN）进行模糊关联规则挖掘，将PSO 算法应用于WFNN 的优化，寻找合适的可变阈值wb，可变权重wc、we和wf。WFNN 中权重we的值象征一个模糊规则，当其值很小时，该规则为模糊冗余规则，需要进行裁剪。之后再根据有效规则确定模糊神经网络的结构。Boomilingam 等人[73]引入边缘灰度共生矩阵和人工神经网络对图像增强特征进行关联规则挖掘，使用改进的PSO 算法优化人工神经网络的权值，把经典Apriori 算法挖掘出的规则作为FFBNN 的输入类别，使用改进PSO 算法的ANN 在精度、召回率和准确率等方面都有提高，检索准确率从90%提高到95%。

PSO 算法能直接与人工神经网络进行混合，Kuo等人[74]混合了TD-FP-growth（top-down FP-growth）算法[75]、最佳人工免疫网络[76]（optimiz ation artificial immune network，Opt-aiNet）和PSO 算法解决供应商选择与订单分配问题。TD-FP-growth 算法对现有供应商数据进行关联规则挖掘，确定每个供应商的重要性，选择出关键供应商，aiNet-PSO（Opt-aiNet PSO）方法以最小成本为关键供应商分配订单量。OptaiNet 具有产生抗体、克隆抗体及变异等特性，不易陷入局部最优，同时PSO 算法对Opt-aiNet 中的每组抗体进行优化，加快算法的收敛。

5 PSO 算法在关联规则挖掘中的应用

在处理复杂的现实优化问题时，智能算法引导群体方向进行逐步搜索直至获得解决方案，此类算法在搜索过程中不受优化函数形态的约束，适应性强、运行效率高，因此被应用于各种领域，并且在解决大多数高度非线性和多模态的优化问题方面表现良好[27]。与精确算法相比，智能算法在解决关联规则挖掘问题时由于随机搜索的特性可能不会获取全部解决方案，但能在合理的时间内获得足够好的解决方案。

随着智能算法在关联规则挖掘中的不断发展，PSO 算法被广泛应用于不同领域。购物篮问题是一类超市商品交易问题，通过对顾客的交易信息进行分析从而对商品进行决策，关联规则挖掘算法主要针对购物篮问题被提出，同时也被广泛用于解决购物篮问题。文献[77]对超市购物数据进行动态关联规则挖掘，提出一种改进PSO 算法的灰色模型，通过增加缓冲算子，引入二次搜索机制对PSO 算法进行改进，优化求解灰色模型不同时刻的背景值，以提高PSO 算法的局部搜索能力，从而提高灰色模型的预测精度。文献[78]考虑到传统频繁项集挖掘算法主要用于寻找频繁出现的商品组合，而不关注商品的其他属性，比如销量、销售价和进货价等。为了进一步获取具有高利润的商品组合，发现具有高效用（例如，高利润）的项集，提出一种基于高效用项集挖掘[79]（high utility itemset mining，HUIM）的HUIM-IPSO 算法，实验表明该算法具有更高的挖掘效率和更快的收敛速度。HUIM-IPSO 算法的时间复杂度与传统PSO 算法的时间复杂度一致，假设PSO 算法中粒子的数量为m，迭代次数为N，每个粒子每一次迭代需要的运算时间为T，算法总的运行时间为m×N×T。

近些年，PSO 算法由于其实现简单、收敛速度快等优点被成功应用于金融领域，其中股票走势分析需要综合分析各股票涨跌情况、现金流入量、相关政策和GDP 等多种数据信息。传统数学统计分析方法主要针对单一股票信息进行预测，而股票走势往往与同行业中其他公司甚至其他行业的经营情况密切相关，因此对于股票的走势预测准确率不高。同时，股票预测数据具有规模大、维度高、价值密度低和实时性要求高等特点，使用Apriori 算法需要花费大量时间多次扫描数据，容易造成对股票走势的误判与延时，无法适用于实时性极高的股票关联预测分析。基于上述原因，文献[80]提出一种使用协同粒子群优化的股票关联规则挖掘方法用于预测股票走势，主要针对传统数据分析方法对股票走势进行预测时具有准确率不高，时效性不强的缺陷，该方法分别使用PSO 算法对支持度与置信度进行挖掘优化，较Apriori 算法和PSO 算法在准确率与挖掘速率上有了很大的提高。文献[81]同样对股票信息进行挖掘，主要针对投资者的股票交易数据，首先使用PSO 算法优化支持度和置信度的阈值，之后通过阈值筛选出合适的粒子即关联规则，基于PSO 算法的关联规则挖掘方法能挖掘出投资者与购买股票间的关联规则，有利于投资者进行决策。

对于医疗领域，使用传统关联规则挖掘算法生成的规则目标单一、数量巨大，需要剪枝、过滤才能获取重要规则，因此，一些学者开始使用PSO 算法进行医疗信息关联规则挖掘。医学影像和计算机视觉的快速发展，从庞大的数据库中管理和检索医学影像变得越来越困难。文献[73]使用PSO 算法及人工神经网络对医学图像进行关联规则挖掘，提出一种改进后的医学图像检索系统，能有效支持医生的诊断任务，方便对图像数据库进行检查及搜索，具有很强的实用价值。文献[82]提出一种基于PSO 算法、支持向量机[83]（support vector machine，SVM）及Apriori算法的模型用于诊断红斑鳞状疾病。该模型使用Apriori 算法从原始特征集中分离冗余疾病特征，降低数据集维度，之后使用PSO 算法优化SVM 模型，对多个患者的疾病特征进行分类，由于PSO 算法能有效确定SVM 的参数值，有利于提高SVM 模型的分类精度，即对疾病的诊断准确度。

工业产品在生产过程中包含大量设计、工艺、制造和装配信息等历史数据，对产品知识的挖掘与重用已成为企业所使用的重要手段之一，关联规则挖掘也常被应用于工业生产领域，包括产品族设计知识的挖掘，产品设计与制造的映射关系识别，生产过程中质量控制规则的挖掘，以及工艺序列知识等。文献[84]使用BPSO 算法对卫星典型件工艺知识进行关联规则挖掘，主要针对卫星典型件在工艺设计过程中设计任务量大、重复性工作多且其历史工艺数据未能充分有效利用的问题，通过建立工艺知识的关联规则模型，引入BPSO 算法对规则进行处理，有效提高工艺知识的挖掘效率。文献[36]对机床加工零件进行关联规则挖掘，使用基于BPSO 的关联规则挖掘方法，从数据中提取有用的工艺知识反映产品设计与制造的映射关系，且引入相似度指标以消除无效规则。

对于风险评估领域，关联规则挖掘方法适用于分析各事件间存在的内在联系，为风险预测、响应及防范提供决策依据，但随着社会的发展该领域包含了大量复杂数据，具有时间、地点、原因、造成的伤亡和损失等多个属性，仅单独使用传统关联规则挖掘算法效率较低，因此文献[85]对社会安全事件进行关联规则挖掘，提出PSOFP-growth 算法，该算法使用PSO 算法获得最优支持度，通过5 000 个包含时间、地点、攻击目标和死亡人数属性的社会安全事件数据构造FP-tree，以信息熵为兴趣度指标用于衡量关联规则的有效性，消除无效关联规则。文献[55]采用改进PSO-Apriori算法寻找数据库中所有具有强内在关联特征的恐怖组织信息，筛除不满足要求的频繁项集，通过对挖掘出的恐怖组织关联特征进行分析发现中东和北非、南亚和撒哈拉以南的非洲地区的恐怖组织具有较强的关联关系。关联规则挖掘同样是洪灾风险分析的重要方法之一，用于减轻洪水带来的灾害损失与影响[86]。洪灾风险评价涉及自然、技术、社会经济等诸多影响因素且国内外尚无统一的评价指标体系和评价标准，因而洪灾风险评价一直是国内外灾害学研究的难点和热点。文献[87]提出了一种基于PSO 规则挖掘算法（PSO-Miner）的洪灾风险评价模型，对北江流域进行洪灾风险评价，该算法使用实数型编码方式，每个粒子对应一条路径，相应产生一条评价规则，规则为评价指标节点和洪灾风险等级节点的连线。由文献[85]、[55]和[87]可知，基于PSO 算法的关联规则挖掘方法可能搜索不到所有有效关联规则，而且当粒子个数和迭代次数较大时算法运行时间相对较长，但为风险领域的智能化评价提供了一种新的解决思路。

6 总结与展望

PSO 算法在关联规则挖掘中的研究作为一个较新领域，通过学者们的探索与深入，在算法的设计及优化方面日趋成熟，并广泛应用于购物篮分析、金融、医疗、工业生产及社会安全等领域。本文总结了关联规则挖掘中针对PSO 算法的改进研究，改进方法主要有以下几种：（1）基于参数的改进，对惯性权重、社会学习因子及自我学习因子等参数进行改进；（2）基于变异策略的改进，粒子有一定概率进行改变；（3）将PSO 算法与其他算法混合，避免使用单一算法而形成的缺陷。

随着数据的爆炸增长，从中挖掘到有效关联规则越来越困难，因此，该领域在未来研究中仍是具有挑战性的方向，未来的研究工作重点可能主要在以下方面：

（1）PSO 算法是一种随机搜索算法，解决包含大量高维数据的问题时效率较低，仅使用单台计算机无法满足运算的需求，而分布式、并行运算的关联规则挖掘算法能显著提高运行效率。目前关于这方面的研究较少，大部分研究都是并行化经典关联规则挖掘算法，如：基于Hadoop Map-Reduce 模型的Apriori 算法[88]和FP-growth 算法[89]，基于Spark RDD框架的Eclat 算法[90]等，而PSO 算法具有本质并行性，每个粒子都是独立个体，其适应度值计算及运动过程都是并行的[91]。因此，设计并行化PSO 算法更为有效地处理海量数据关联规则挖掘是值得深入研究的课题。

（2）目前，针对PSO 的关联规则挖掘算法的缺陷已经提出了许多改进算法，但对粒子初始化方法进行改进的相关研究较少，大部分文献中使用随机初始化，这种初始化方法容易导致粒子分布不均匀，产生的粒子质量不高，大部分粒子可能远离最优解，影响算法的全局收敛。一般而言，初始粒子群应在有限的数量内最大限度地表征解空间包含的信息，在迭代早期粒子能深入探索寻找最优解，实现算法收敛性和快速性的协调统一。目前在传统PSO 算法领域中运用较为广泛的初始化改进方式有混沌初始化[92]、聚类初始化[93]及非线性单纯体法（nonlinear simplex method，NSM）初始化[94]。混沌初始化利用混沌序列的遍历性，产生大量初始群体，从中挑选出优秀粒子，优化初始群体的质量，同时增加粒子遍布整个解空间的可能性，但不能确保其完全均匀分布。聚类初始化利用聚类算法挖掘初始粒子群的信息，从每个子群的聚类中心中筛选出具有代表性的粒子，进而缩小了初始种群的规模，提高了粒子质量，但没有彻底解决初始粒子在解空间中分布不均匀的问题。非线性单纯体法克服了随机初始化不能保证粒子合理分布的缺点，通过反射、扩张等运算，使其产生的各个顶点可充分体现函数解空间中的峰谷特性，对提高初始粒子质量，加速PSO 算法的收敛速度起到了有效的作用，但该方法复杂性较高，需要较多的运算时间。关联规则挖掘领域涉及各种数据类型及函数形态，与传统PSO 算法领域使用的统一基准测试函数不同，因此针对不同类型设置初始化方式是一项较为困难的工作。同时作为未来研究的一个方向，关于粒子群初始化改进可以参考上述提及的初始化方法思想，设计更为优秀的种群初始化方式，提高算法的运行效率。

（3）现有研究中，基于PSO 的关联规则挖掘算法虽已被成功运用于多种领域，但涉及现实生活中的应用领域仍然有限，针对大部分领域的应用还处于初步阶段，相关研究较少。因此，研究新的关联规则应用领域，在应用的广度和深度上进行拓展都是很有价值的工作。