从一道高考题谈与函数零点有关的变量取值范围问题
浙江省兰溪市第一中学(321102) 张城兵
函数零点是函数、方程与不等式三个知识块联系的重要桥梁,因而知识点的重要性就不言而喻了,由它产生的题目简约而不简单,内涵丰富,意境深远.多种知识和解题技巧组合在一起,往往让学生无从下手,或者中途夭折.笔者选取一些典型的例子,予以剖析,以飨读者.
例1(2015年高考浙江文科第20 题) 设函数f(x) =x2+ax+b(a,b ∈R).
(1) 略; (2) 已知函数f(x) 在[-1,1] 上存在零点, 0 ≤b-2a≤1,求b的取值范围.
解法一这是当年浙江省文科高考压轴题,至今让人津津乐道,回味无穷.考生首先想到方法一,但庞杂的不等式组和难画的线性规划图,使学生很难做全对,由方程f(x) = 0在[-1,1]上有实根及已知,得

图1
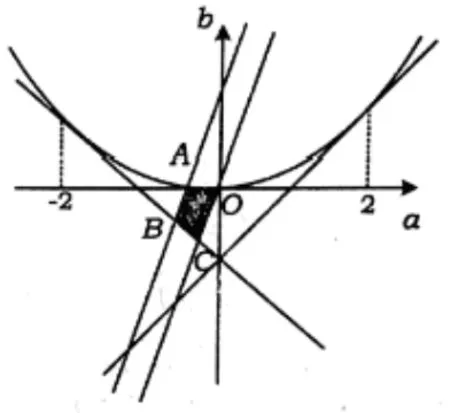
图2
解法二(官方的标准答案) 设s,t为方程f(x) = 0的解, 且-1 ≤t≤1, (笔者注: 因为题目告知函数f(x)在[-1,1] 上存在零点, 个数不明确, 所以只要保证其中一个零点t ∈[-1,1],s模糊处理), 则由于0 ≤b-2a≤1,因此(-1 ≤t≤1).当0 ≤t≤1 时,由于和≤9-所以当-1 ≤t <0 时,由于-2 ≤<0和-3 ≤<0,所以-3 ≤b <0.故b的取值范围是[-3,9-
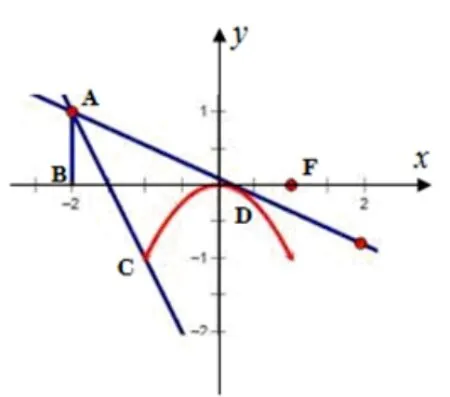
图3
解法三函数f(x) 在[-1,1] 上存在零点, 也就是g(x)=ax+b与h(x)=-x2在x ∈[-1,1]上有交点,而条件0 ≤b-2a≤1 意味着函数g(x) =ax+b图象过横坐标为-2,纵坐标在[0,1]上变化的点,也即为线段AB上的任意一点,且它与抛物线段有公共点,如图3,求截距b的范围.由图可知,直线BC、BD不符合要求, 直线AC、AD符合要求, 找它们与抛物线段有公共点的临界状态时b的值即为所求.易求AC的方程y=-2x-3,令AD的方程y-1=k(x+2)与y=-x2联立,得x2+kx+2k+1 = 0,若直线AD与抛物线相切,由Δ =k2-8k-4 = 0,得k= 4±取k= 4-(因为x ∈[-1,1] 的限制, 故k= 4 +舍去), 所以截距b=9-综上,b的取值范围是[-3,9-
评注方法一是学生首先想到方法,毕竟这也是学习函数零点后常用方法,但是它的复杂程度超乎想像;方法二是很创意的,用确定区间上的零点来充当自变量,特别是对另一个零点s的模糊处理是神来之笔;方法三更胜一筹,达到数形结合的最高境界.
下面笔者以零点个数为标准,分门别类剖析.
一、零点个数明确,以零点为自变量
例2(2017年浙江省数学竞赛题) 已知函数f(x) =x2+ax+b(其中a,b ∈R),在区间[0,1]内有两个零点,则a2-2b的取值范围是____.
解析设零点为x1,x2∈[0,1] 且x1/=x2, 则x1+x2=-a,x1x2=b, 此时,x1,x2是独立变量, 各自可取到最大或最小值, 只是要考虑不相等即可, 所以a2-2b=
例3已知函数f(x) =x2+ax+b(a,b ∈R)在区间(0,1)和(1,2)上各有一个零点,则a2+a-2b的取值范围为____.
解析设两零点为x1,x2,且x1∈(0,1),x2∈(1,2),则a2+a-2b的取值范围为
例4(2014年浙江省数学竞赛第18 题)已知b,c ∈R,二次函数f(x)=x2+bx+c.在(0,1)上与x轴有两个不同交点,求c2+(b+1)·c的取值范围.
解析令r,s为二次函数的两个零点(r /=s), 则f(x) = (x - r)(x - s), 易知r+s=-b,rs=c, 所 以c2+(b+1)·c=c(c+b+1)=rs(1-r)(1-s)≤因为r /=s,所以等号不成立,故c2+(b+1)·c的取值范围是
评注此三例零点明确有几个,并在哪个区间,此时的零点就是自变量,并且取值范围也知道了,将所求的代数式转化为以零点为自变量的函数,尽管有两个自变量,但它们是独立的,所以取值范围不难求,这是一种常规方法.
二、零点个数模糊,选一个独挡一面
例5已知函数f(x) =x2+ax+b(a,b ∈R)在[0,1]上至少有一个零点,则a2+2b的取值范围是____.
解析零点个数不明确, 题干中又未要求予以讨论, 此时解法可能与零点个数无关,故只需选某个零点为x0,x0∈[0,1],当然此时不能用韦达定理了,而改用方程实根的定义(函数的零点实质就是方程的实根),则+ax0+b= 0,即b=0,所以a2+2b=a2-2ax0-,这是有两个变量的函数,a与x0没有明显的制约关系,故可以先看作以a为主元的二次函数,求得(a2+2b)min=-,再以x0为主元,因为x0∈[0,1],故a2+2b ∈[-3,0].
例6已知函数f(x) =x2+ax+b(其中a,b ∈R)在区间(0,1]内有零点x0, 则的最大值是____.
解析令零点为x0,x0∈(0,1],则+ax0+b=0,即b=0,所以
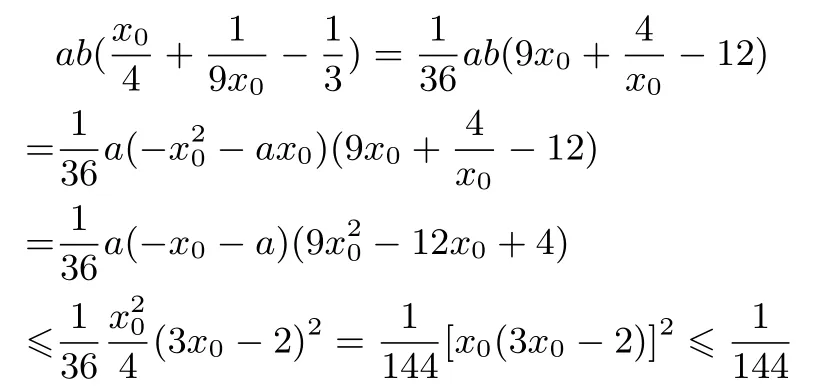
此例解法与前一例一脉相承,只是求最值难度加大,有更强的技巧性.
例7已知二次函数f(x) =ax2+bx+c有零点, 若(a-b)2+(b-c)2+(c-a)2≥Ma2恒成立,则实数M的最大值是____.
解析由已知b2≥4ac,则y,则x2≥4y,由(a-b)2+(b-c)2+(c-a)2≥Ma2,得进而M≤(1-x)2+(x-y)2+(y-1)2=2y2+2x2-2x-2y-2xy+2,令g(y)=2y2+2x2-2x-2y-2xy+2=2y2-(2+2x)y+2x2-2x+2,此时看作关于y的二次函数,定义域为
1) 当对称轴y=即x≥ 1 +或x≤1-g(y)min=从而
2) 当y=即时,+2x2-2x+2 =-2x+2,g′(y)=+3x+2=令g′(y) = 0,得x= 1 为极小值点,故g(y)min=所以M≤从而实数M的最大值是
评注例5、例6 零点个数不明确,我们可以在规定区间内选一个记作x0,但无法只用x0来表示所求代数式,所以借助主元方法,先来后到,确保x0用在最后,而例7 不用设零点,这是由所求问题决定的,利用齐次式,达到减元目的.
三、三个或四个函数的零点问题的处理
例8若函数f(x)=2x3+mx2+nx+t在(0,1)上有三个不同的零点,则f(0).f(1)取值范围是____.
解析令f(x)=2(x-x1)(x-x2)(x-x3),(x1,x2,x3互不相等)则f(0).f(1)=-4[x1(1-x1)][x2(1-x2)][x3(1-(用均值不等式,但等号取不到),所以f(0).f(1)取值范围是
例9已知函数f(x)=x+,g(x)=f2(x)-af(x)+2a有四个不同的零点x1,x2,x3,x4,则[2-f(x1)]·[2-f(x2)]·[2-f(x3)]·[2-f(x4)]=____.
解析令t=f(x),则y=g(x)=t2-at+2a,因为g(x)有四个不同零点x1,x2,x3,x4,故t2-at+2a=0 有两个不等实根t1,t2且t1+t2=a,t1t2=2a,所以2(t1+t2)=t1t2,令f(x1)=f(x2)=t1,f(x3)=f(x4)=t2,所以[2-f(x1)]·[2-f(x2)]·[2-f(x3)]·[2-f(x4)]=[(2-t1)(2-t2)]2=16.
例10设x1,x2是a2x2+bx+1 = 0 的两实根;x3,x4是ax2+bx+1=0 的两实根.若x3<x1<x2<x4,则实数a的取值范围是____.
解析当a >0, 如图4,g(x1)<0 =f(x1), 所 以得a >1;当a <0,则g(x2)>0=f(x2),求得解得0<a <1,矛盾,故a的取值范围是(1,+∞).
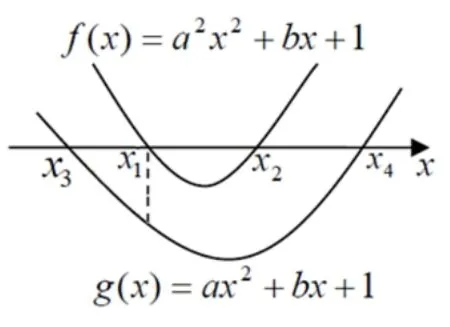
图4
评注零点个数增加,并不影响方法,只是增加学生理解难度.
四、反弹琵琶型——函数不存在零点
例11已知f(x)=x2-2x+c,f1(x)=f(x),fn(x)=f(fn-1(x))(n≥2,n ∈N*),若函数y=fn(x)-x不存在零点,则c值的取范围是____.
解析当f(x) =x无解时, 用判别式得c >此时f(x)>x恒成立, 则f2(x)-2f(x) +c=x <f(x)即f2(x)-3f(x) +c <0 此时仍无解, 由数学归纳法,y=fn(x)- x无零点.而当c≤时,f(x) =x有解,则y=fn(x)-x存在零点.所以c值的取范围是
评注学生习惯顺向思维,突然出现逆向思维的问题,对他们来说很难摆脱定势干扰,就好比说研究在某某区间单调性,一般学生没问题,但突然要求在某区不单调,就会手忙脚乱.
读者对下面练习不妨一试:
1.若函数f(x) =x2+2ax+b,(x ∈[1,2])有两个不同的零点,则a+b的取值范围为( )
A.(0,3] B.(0,2) C.(1,3) D.[0,3]
2.已知函数f(x) =x2+ax+b(其中a,b ∈R),在区间[0,1]上有零点,则ab的最大值是____.
3.已知二次函数f(x) =ax2+bx+c(a,b,c ∈N*),函数f(x)在上有两个零点,则a+b+c的最小值为____.
4.已知a,b ∈R 且0 ≤a+b≤1,函数f(x)=x2+ax+b在上至少存在一个零点, 则a-2b的取值范围是____.
5.已知关于x的方程x2+2bx+c= 0(b,c ∈R) 在[-1,1]上有实数根,0 ≤4b+c≤3,则b的取值范围是____.
6.(2017年福建省数学竞赛题) 若关于x的方程x2+ax+b -3 = 0(a,b ∈R) 在区间[1,2] 上有实根,则a2+(b-4)2的最小值为____.
7.若a,b,c为正整数,方程ax2+bx+c= 0 的两个实数根x1,x2满足-1<x1<x2<1,求a+b+c的最小值.
参考答案1.B 2.3.41 4.[0,1] 5.[-1,2] 6.2 7.最小值为11.

