一道双曲线题的探究
四川省名山中学(625100) 高继浩
一、题目呈现
题目(笔者自编题)已知双曲线的左,右焦点分别为F1,F2,过F2的直线l交双曲线Γ 的右支于A,B两点,若ΔABF1的内切圆半径为则直线l的斜率为____.
如图1, 看到题目中的“内切圆”三个字, 比较自然地会想到利用ΔABF1的面积找关系,通过两种面积法列方程求解,最终落脚于数学运算.该题在测试中的得分率很低,主要原因是多数学生在有限的时间内算不出,也找不到其他方法.

图1
二、题目解答
解法1设直线l的方程为x=ty+ 3,A(x1,y1),B(x2,y2), 联立直线l与双曲线Γ 的方程, 消去x得(4t2-5)y2+24ty+16=0,Δ=320(1+t2),由y1y2<0知4t2-5<0,故|y1-y2|=由双曲线定义知|AF1|=|AF2|+|BF1|=|BF2|+从ΔABF1的面积出发,有
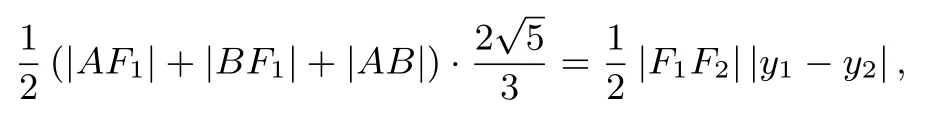
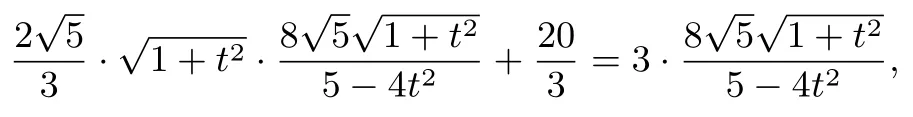
令u=化简整理解得u=故t=即直线l的斜率为±2.
解法2如图1,设ΔABF1的内切圆圆心为C,圆C分别与AF1,BF1相切于点D,E.若圆C与AB相切于点P,且点P位于线段AF2(不包括端点)上,则

由|DF1|=|EF1|知①与②矛盾; 若切点P位于线段BF2(不包括端点) 上, 同理可得矛盾.故切点P只能与F2重合.连接CD,CF1和CF2,不妨设直线AB的倾斜角为锐角α,则∠CF2F1=在ΔCF1F2中,由余弦定理知
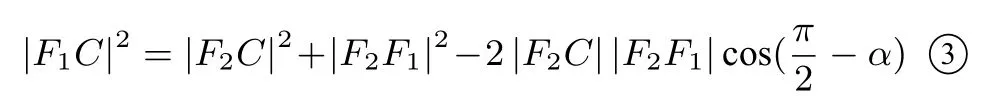
而
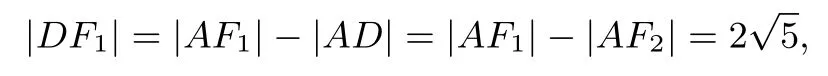
故|F1C|2=|CD|2+|DF1|2=代入③可得sinα=tanα= 2,由图形的对称性可知直线l的斜率为±2.
解法1 自然但运算偏繁,解法2 中注意到F2是切点使得运算量较小.
三、题目推广
命题1若双曲线= 1(a >0,b >0)的左,右焦点分别为F1,F2,过F2的直线交双曲线的右支于A,B两点,则ΔABF1的内切圆与AB相切于点F2.
命题2若双曲线= 1(a >0,b >0)的左,右焦点分别为F1(-c,0),F2(c,0),过F2且倾斜角为α的直线交双曲线的右支于A,B两点, ΔABF1的内切圆半径为r,则r=
采用题目解法2 的前半部分即可证得命题1,分α为锐角、钝角和直角三种情况,采用题目解法2 的后半部分不难得到命题2,读者不妨一试.
同理可得:
命题3若双曲线= 1(a >0,b >0)的下,上焦点分别为F1(0,-c),F2(0,c),过F2且倾斜角为α的直线交双曲线的上支于A,B两点, ΔABF1的内切圆半径为r,则r=
四、拓展探究
命题4若椭圆= 1(a >b >0) 的左, 右焦点分别为F1(-c,0),F2(c,0), 过F2且倾斜角为α /= 0 的直线交椭圆于A,B两点, ΔABF1的内切圆半径为r, 则
证明设A(x1,y1),B(x2,y2), 直线AB的方程为x=my+c,与椭圆方程联立,消去x得
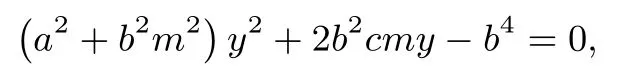
则y1+y2=从ΔABF1的面积出发,有
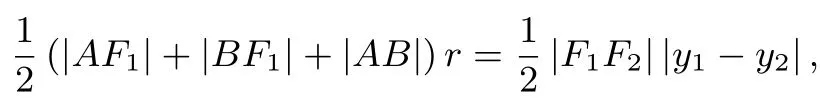
即2ar=故r=因为m=所以r=
同理可得:
命题5若椭圆= 1(a >b >0) 的下, 上焦点分别为F1(0,-c),F2(0,c),过F2且倾斜角为α /=的直线交椭圆于A,B两点, ΔABF1的内切圆半径为r, 则
抛物线只有一个焦点, 联想到焦点关于顶点的对称点,探究得到如下结果.
命题6若抛物线y2= 2px(p >0)的焦点F关于原点的对称点为C,过F的直线交抛物线于A,B两点,则直线AC和BC的倾斜角互补.
证明设易得y1y2=-p2,故所以直线AC和BC的倾斜角互补.
命题7若抛物线y2= 2px(p >0)的焦点F关于原点的对称点为C,过F且倾斜角为α的直线交抛物线于A,B两点,ΔABC的内切圆半径为r,则r=
证明不妨设点A在x轴上方, 设直线AC的方程为x=my -(m >0), 与抛物线方程联立, 消去x得y2-2pmy+p2= 0,Δ = 4p2(m2-1)≥0.从ΔABC的面积出发,有
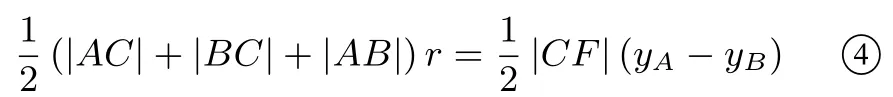
(1)当α=时,kAC= 1,m= 1,Δ = 0,直线AC与抛物线相切,由④可得r=满足r=
(2)当m >1 时,Δ>0,设直线AC与抛物线的另一交点为D,A(x1,y1),D(x2,y2), 则由命题6 知B(x2,-y2).因为y1+y2= 2pm,y1y2=p2, 所以|x1-x2|=m|y1-y2|=故|kAB|=设∠ACF=∠BCF=θ,则从而
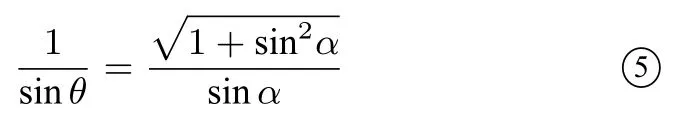
在ΔACF中, 由正弦定理有故|AC|=在ΔBCF中,同理有|BC|=所以|AC|+|BC|=又因为yA -yB=|AB|sinα, 代入④化简得=psinα, 结合⑤得r=
综上,命题得证.
同理可得:
命题8若抛物线x2= 2py(p >0)的焦点F关于原点的对称点为C,过F且倾斜角为α的直线交抛物线于A,B两点,ΔABC的内切圆半径为r,则r=

