大网目底拖网在稳定流场中的数值模拟

王永进，万 荣，张 勋，张 禹，刘龙腾，王鲁民

（1.中国水产科学研究院东海水产研究所，上海 20090；2.上海海洋大学，上海 201306；3.中国水产科学研究院，北京 100141）

底拖网是一种复杂的锥形网具，为了设计或优化拖网渔具，研究方法主要包括模型试验、海上测试和数值模拟，来分析和评估在实际作业中现有渔具（或新设计渔具）的水动力性能［1］。但是，渔具模型试验或海试需要花费较多的人力和成本，而计算机技术的进步推动了模拟柔性渔具数值方法的发展。

柔性渔具数值计算方法之一是将网目看作一组集中质量的点和弹簧杆件，质量点代表节点，杆件代表目脚。LEE等［2-3］首先采用集中质量法建立网片、拖网和围网网具系统的数学模型，计算水下柔性网具的形状和运动状态；BESSONEAU等［4］建立了网衣的力学平衡方程进行求解，开展了水流中拖网变形和受力情况的分析；还有学者对网状和实体锥形结构［5］以及特定的网片［6］等进行了仿真分析，以便能通过可视化技术呈现网具的形状和受力情况；万荣等［7-10］将其应用于稳流中网片、中层拖网以及网箱的形状变化和受力情况研究，得到了良好的模拟效果，并发展了适用于网箱网目群化计算以及渔具模型空间形状的计测方法；陈英龙等［11］构建大型中层拖网模型，并利用三维仿真呈现出瞬时作业状态，分析了拖网网具的张力分布。另一种方法是通过将网片离散成三角形单元进行网具形状计算［12］，克服了目脚单元的目脚必须与网线平行的缺陷，通过此方法，DANIEL PRIOUR［13］以三角形单元离散法计算了网口阻力；在这些研究基础上，AMELIA等［14］以1D杆单元模拟绳索，2D三角形单元模拟网片，比较分析了底拖网渔具在静态平衡时形状的两种数值方法 牛顿-拉斐尔迭代法和动态仿真法，研究表明后者计算结果较稳定但计算过程较慢。

根据以上研究，虽然数值模拟在计算网具形状和受力等方面取得了一定的效果，但在建模过程中，由于拖网网具系统规模庞大，结构复杂，网目繁多，或因计算机能力的限制，如果在有限元分析中单纯以实际单元进行数值计算，将导致计算量巨大而难以实现。为此，BESSONEAU等［4］在拖网数值计算中提出了网目群化的概念，即根据实际需要可以用1个虚拟的计算网目代替一定数量的实际网目，从而减少拖网的计算单元数。IGOR等［15］也提出了等效杆单元的概念，试图以有限个等效杆单元替代部分网衣单元，以提高计算效率。万荣等［10］提出了一种适用于网箱耐流特性有限元分析的网目群化方法，验证了其可行性，并讨论了不同流速和配重条件下网目群化数目对计算结果和计算效率的影响。DANIEL PRIOUR等［12］提出的三角形有限单元离散网片实质也是一种网目群化的概念。网目群化是在网箱、拖网等渔具数值模拟上提出并应用，目前，除万荣等［10］较详细介绍了适用网箱的群化方法，其他学者均未对网目群化提出具体的描述。另外，万荣等的方法并不完全适用于拖网、张网等更为复杂的网渔具。

大网目拖网网目尺寸变化快，网身部位分段多，手工编织的网片纵向目数少且存在较多的挂目或合并目。本文采用集中质量法，将网衣网目离散为一系列在两端节点处通过无摩擦铰接而成的柔性集合体，建立大网目底拖网的数值模型，模拟其在稳流状态下受力及形状变化。在保证准确性的前提下，为了减少计算量以提高计算效率，提出一种适用于拖网渔具数值计算的网目群化方法。同时，利用此群化方法，对同一顶拖网进行不同网目数量的群化，并对比水槽试验结果，验证此方法的实用性以及拖网渔具数值模拟的准确性。

1 材料与方法

1.1 物理模型

所选母型网为中国东海广泛使用的大网目底拖网，属于单船有翼单囊拖网。物理模型根据田内准则设计制作，大尺度比设为1∶35，模型图见图1。物理模型网全网网线直径均为0.5 mm。网口部分及袖网网目尺寸为514mm，其他网身各段网目尺寸为450 mm到10 mm不等。上纲长度为6 214 mm，下纲长度为6 271mm。沉子纲空气中重175 g，总浮力为126 g，有8个14 g浮球，2个7 g的浮球。网身部位网衣具体规格见表1。

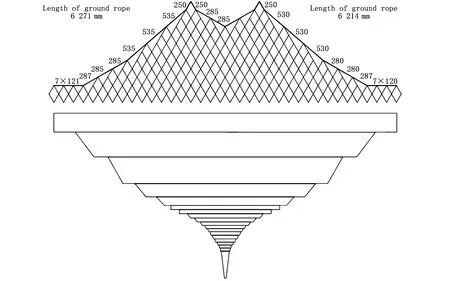
图1 拖网物理模型网衣展开图Fig.1 Unfolded draw ing of traw lmodel

表1 拖网物理模型网身部位网衣规格Tab.1 Specifications of body netting of traw lmodel

1.2 仪器与设备

物理模型试验在中国水产科学研究院东海水产研究所的静水槽中实施。静水槽规格为长90 m×宽6 m×深3 m。试验测试时的水深为2.81 m，水槽底部为光滑的陶瓷砖。

水槽拖车车速范围为0～4.0 m·s-1，配有微处理机调速系统，相对精度为P≤1%；光电测速仪精度为±0.01%；空纲前端连接Lu-A型测力传感器（日本），进行测力，量程为100.00 N，数据单位为g，测力仪器的线性误差小于满量程的0.05%；小型鱼探仪StructureScan（墨西哥）用于测量网口的垂直扩张，距离分辨率为30.00 mm［16］。

1.3 数值方法

1.3.1 基本假设

本文将拖网网目单元作为空间索杆单元进行处理，在对网目单元解决几何非线性平衡方程时，对网线材料、变形特性等方面作如下基本假定：

1）网线绝对柔软，且只能承受拉伸应力；

2）绳索和网线材料各向同性，并且符合应力与应变的弹性虎克定律，且属于弹性范围内的小应变；

3）单元无摩擦铰合，单元张力仅作用于单元的轴线上，并且在单元的整个横截面上均匀分布且无衰减；

4）外载荷作用力视作作用在杆件的节点上，即杆件单元不发生弯曲，杆件内仅有轴向内力。

底拖网在作业时，其下纲与海底接触，下纲与海底之间会产生摩擦力，同时由于边界层的存在，使下纲及下部网衣处的流场会产生变化。本研究中，对“海底”—— 即静水槽槽底作如下假设：

1）水槽底部是等深平整的，底部摩擦系数相同；

2）忽略边界层产生的流场变化对拖网形状和张力的影响；

3）流场中没有波浪的影响，拖网是在定常流中运动。

1.3.2 基本方程

当网具在稳流中运动时，构成网衣的单元会产生相对位移，从初始位置到形状变化后的状态。对于整个网具系统，其总的势能可描述为［7］：

式（1）中，П是网具系统总势能，Fi是作用在第i个节点上的等效节点力，Di是单元i端的节点位移，Tg是第g个单元的轴向力，Lg0是第g个单元的初始长度，Lg是第g个单元变形后的长度，Ag是第g个单元或目脚的横截面积，E是材料的杨氏模量，f是节点自由度，m是单元数量。

由于张力或在大变形中单元有限位移，第g个单元的伸长量［Lg（Di）-Lg0］可描述为：

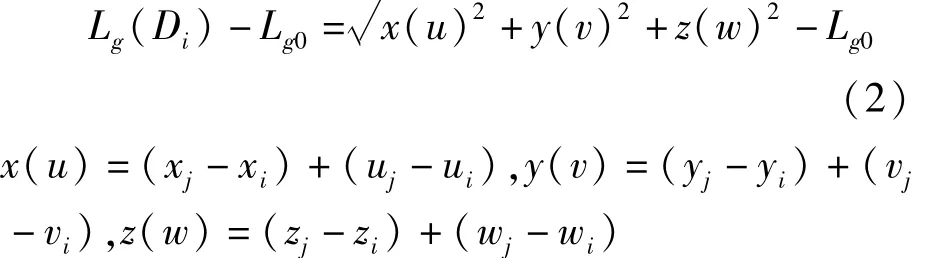
式（2）中，x、y、z是单元分别在x、y、z方向的节点坐标。x轴和z轴分别表示水流方向和水深方向的反向。y轴垂直于xz平面。变量u、v和w表示单元在x、y和z方向的节点位移。下标i和j表示单元的两端。Di是单元i端的节点位移，Lg是第g个单元变形后的长度，Lg0是第g个单元的初始长度。

根据最小势能原理，当这个离散系统处于平衡状态时，也就是整个拖网系统在水流作用下处于平衡状态时，系统的势能最小。对于具有两个独立变量的能量泛函数表达式，其最小值就是泛函数的驻点。由式（1）对Tg求变分，可以得到张力的驻值表达式：

根据上式，各个单元的应力-应变关系表达式为：

式中，П是网具系统总势能，Tg是第g个单元的轴向力，m是单元数量，E是材料的杨氏模量，f是节点自由度，Lm是第m个单元变形后的长度，Df是单元f端的节点位移，Ff是作用在单元f端等效节点力，Ag是第g个单元或目脚的横截面积，Lg是第g个单元变形后的长度，Lg0是第g个单元的初始长度，Di是单元i端的节点位移。

根据作用在目脚上的水动力公式：

式（5）中，R是作用在目脚上的水动力，CR是水动力系数，d是单元直径，L是单元长度，V是水流的相对速率，ρ是流体密度。

当l、m和n分别表示变形后单元对于x、y和z轴的方向余弦，则水动力系数CR（Cx、Cy和Cz为3个方向的水动力系数）表示为：

式（6）中，C0为单元与水流垂直时的水动力系数，通常来讲，水动力系数取决于根据单元直径计算出来的雷诺数（Re），在一般的网箱和拖网研究中，水动力系数一般为2×103～6×103，故取C0为1.3［17］。

本文中摩擦力计算公式为：

式（7）中，fm为底纲与水槽底部的摩擦力，μ为底纲（铁链）与水槽底部（瓷砖）的摩擦系数，其值约为0.1，FN为渔具模型对水槽底部的正压力。

1.3.3 网目群化方法

为了精确地模拟拖网的形状和受力，考虑作用于拖网网衣及纲索所有单元的水动力是非常必要的。但由于拖网系统规模大，导致其计算量巨大或耗费较长时间或难以实现。为此，有的学者引入“网目群化”概念，并提出群化的原则为［3，10］：

1）保持群化前后网片投影面积相等。在保证几何尺度相似时，假若网形相似，则网片与水流的冲角相似，则需要有相同的线面积（将结节分散到各个单脚）；

2）保持群化前后网片的水动力相等。网片的水动力与网片的线面积、网片与水流的冲角相关，若冲角和线面积相等，则网片受到的水动力即相等；

3）保持群化前后网衣的重量相等。

水动力基本公式为［18］：

式（8）中，R为网片受到的水动力，ρ为流体密度，CDN为水动力系数，ST为网片的投影面积，V为流体流动速度。

根据群化前后单元所承受的水动力相等的原则，在水动力计算时，ρ、CDN、ST、V在网目群化前后保持一致。因为需要群化前后网具的形状基本保持一致，则群化前后网衣与水流的冲角基本相似，则线面积保持一致（不考虑结节，或将结节平均分到相连的各个单脚）。

根据线面积计算公式：

式（9）中，S为网片的线面积，N为网目数量，a为目脚长度，d为目脚直径。则有：

式（10）中，d1、N1为群化之前的目脚直径和网目数量，d2、N2为群化之后的目脚直径和网目数量，n为群化目数，即1个群化的虚拟计算网目的目脚所包含的真实网目的网目脚数量，K为群化系数。

根据群化前后所有计算的单元的总重量相等原则：

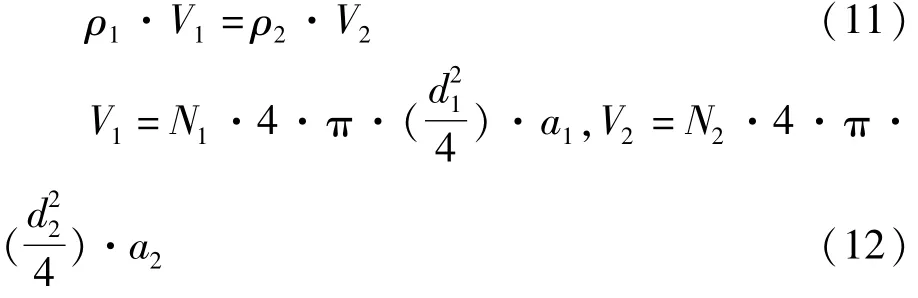
从而得出：

式（11）～（13）中，V1、V2为网目群化前、后网衣的体积，ρ1、ρ2为群化前、后的网线密度，a1、d1、N1为群化之前的目脚长度、目脚直径和网目数量，a2、d2、N2为群化之后的目脚长度、目脚直径和网目数量，K为群化系数。

由于在网目群化中，网衣的重量不变，其重力即不变，而其体积发生了变化，必然导致网衣受到的浮力产生变化，这在研究文献中并没有提及，若未考虑则会导致群化后的网衣所受到的浮力和重力产生较大的影响，因此本文提出在计算网具系统的水动力时，流体的密度不变，而在计算群化网目浮力时，将流体的密度进行修正，使得网目群化前后网衣所受到的浮力和重力的合力相等，由此有公式：

式（14）、式（15）中，Bf1、Bf2分别为网目群化前、后的浮力与重力的合力，ρ水1、ρ水2分别为群化前、后的流体密度，V1、V2为网目群化前、后网衣的体积，g为重力加速度。

由于体积不相等，所以得出：

或者为：

式（16）、式（17）中，ρ水1、ρ水2分别为群化前、后计算网衣浮力的水体密度，V1、V2分别为群化前、后网衣体积，K为群化系数，ρ1、ρ2为群化前、后的网线密度。

由于此网的特点是网目较大，网口及网袖处的网目数较少，为了保持网口部分结构相似，本文只将网身部分进行网目群化，并且群化为两种规格，model-1为单元数为6 513的拖网数学模型，model-2为单元数为1 787的拖网数学模型，两种群化后的拖网数学模型结构规格如表2、表3所示。

表2 model-1拖网数学模型结构参数Tab.2 Structure parameters ofmathematicalmodel ofmodel-1 traw l

表3 model-2拖网数学模型结构参数Tab.3 Structure parameters ofmathematicalmodel ofmodel-2 traw l

1.3.4 数学模型初始位置

拖网是一种由网片、绳索、浮球以及沉子等构成的大规格渔具。为了建立数学模型，将整个拖网网目及绳索离散成有限单元，每个单元包括一个弹性杆件和两个集中质量的点。AMELIA等［14］认为初始位置不必是准确的，但需要给予一定的预加张力。本文将两种规格群化后的拖网初始位置设置为如图2和图3。预加张力为0.1 g。程序编码在MATLAB平台上完成。

图2 m odel-1拖网数学模型初始形状Fig.2 Initially assumed geometry ofmodel-1 traw l net

图3 model-2拖网数学模型初始形状Fig.3 Initially assum ed geometry ofmodel-2 traw l net

2 结果与分析

2.1 流场中拖网形态变化

图4为流速分别在42.9、51.4、60.0、68.6、77.2 cm·s-1时model-1拖网模型展开形态的计算机模拟结果。如图4所示，当拖网受到水流作用时，网口部位从初始位置整体向后方移动，上、下纲和空纲向中间偏移，上中纲向上鼓起，当拖网受力均衡之后，上、下纲均成悬链线状，网衣由初始设置的矩形筒变成圆筒状。袖端及网身网目展开良好，网身后部及网囊部位网衣没有充分展开，网型收缩较快。随着流速的显著增大，网口高度大幅降低，网目张开也越小，网型整体趋于流线型。

图5分别为流速在42.9、51.4、60.0、68.6、77.2 cm·s-1时，model-2拖网模型展开形态的计算机模拟结果。如图5所示，拖网在水流作用下，网口网位从设定的初始位置向后方移动，上、下纲和空纲向内偏移，上中纲向上鼓起，下空纲和下纲Z轴方向没有位移。拖网受力均衡时，上、下纲均成悬链线状，网衣由初始设置的矩形筒变成圆筒状。袖端及网身背部网目展开良好，网身腹部网衣略向上浮起，网囊末端有上翘现象，这可能由于群化后网囊末端网目数极少（仅1目），网目不能很好的展开，受浮力略大的影响而产生上翘。随着流速的显著增大，网口高度大幅降低，网目张开也越小。model-2模型网相较于model-1模型网，网目数少，网目尺寸大，从两者流场中形态的模拟结果看，在相同工况下，两者的形态变化趋势基本相似，特别是网袖及网身部位网衣展开及其形态变化一致。

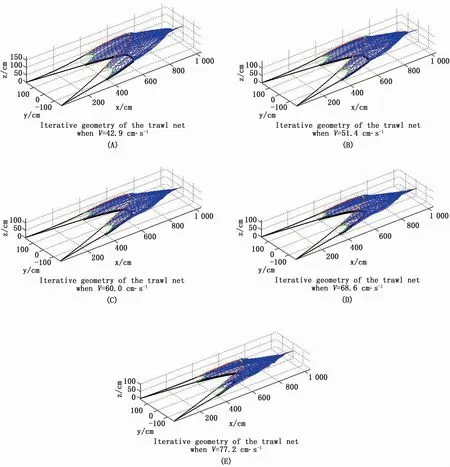
图4 不同流速下model-1拖网模型展开形态Fig.4 Simulated model-1 traw l shape w ith different current velocities

2.2 试验与计算网具阻力比较

图6为水槽模型试验（model）和计算机模拟（model-1和model-2）阻力结果的比较。由图6中可以看出，随着流速由42.9 cm·s-1增加到77.2 cm·s-1，拖网受到的阻力显著增加，而不同速度下，模拟结果均比物理模型试验结果大，且速度越大，计算机模拟的阻力值越大。从图6中也可以看出，群化单元较多的mode-1的数学拖网模型的计算结果与物理模型model的结果非常相近，只是在较大流速下，两者略有差异，群化单元较少的model-2的数学拖网模型的计算结果略大，不同速度下两者相差16%～26%。结果说明，群化单元越多的数学模型的网具阻力计算值与物理模型更相近，群化单元由6 513个减少到1 787个，将会产生20%左右的误差。

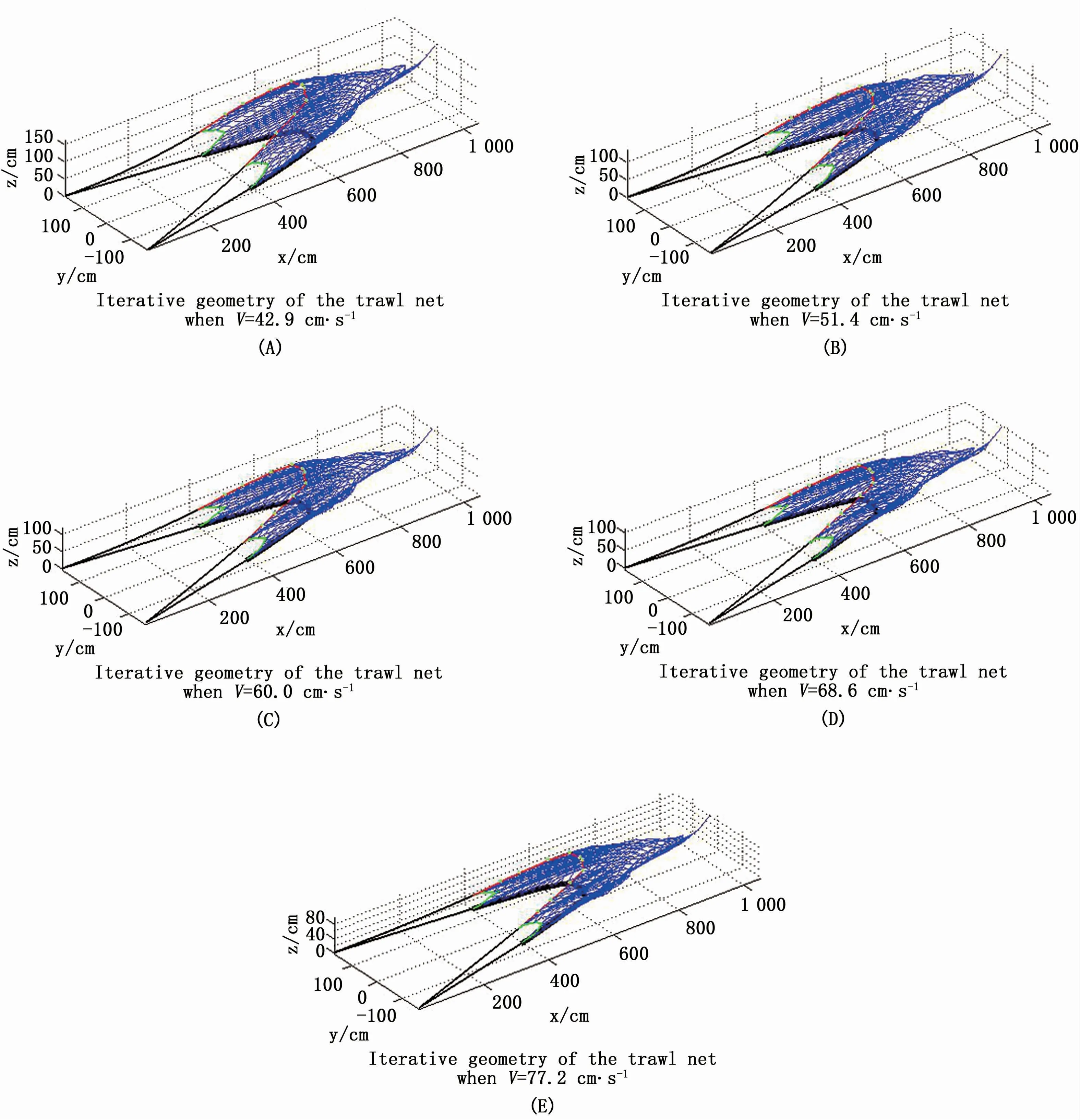
图5 不同流速下model-2拖网模型展开形态Fig.5 Simulated model-2 traw l shape w ith different current velocities

2.3 试验与计算网口垂直扩张比较

图7为水槽模型试验（model）和计算机模拟（model-1和model-2）拖网网口垂直扩张结果的比较。由图7中可以看出，随着流速由42.9 cm·s-1增加到77.2 cm·s-1，网口垂直扩张具有明显的下降趋势，而3者之间的差距不大。当流速较低时，物理模型的网口垂直扩张与群化单元较多的model-1的数值模拟结果相近，而大于群化单元较少的model-2数学模型计算结果；当流速较高时，两种数学模型的模拟结果基本一致，略大于物理模型试验结果。整体上数学模型计算结果与物理模型结果相差5%左右，速度最大时相对误差也仅在10%左右，结果符合良好。

图6 试验与计算的网具阻力比较Fig.6 Com parison of resistance between experiment and calculation

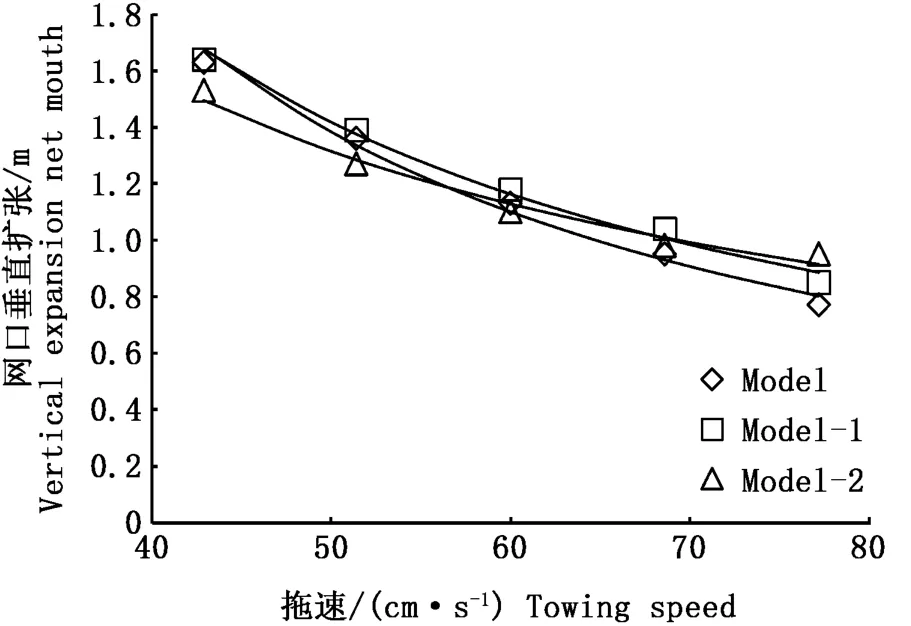
图7 试验与计算的网口垂直扩张比较Fig.7 Com parison of vertical expansion of net mouth between experiment and calculation

2.4 试验与计算袖端水平扩张比较

将模型试验拖网下袖端距离与计算机模拟结果进行比较（图8），图8中实线表示模型试验结果。在拖曳过程中，为了保证水平扩张比为0.35，在试验之前，对网板（拖车牵引杆）间距进行调试，并固定值为3.4 m，通过观测，下袖端间距几乎不变，其距离为2.19 m左右。图中虚线分别为两种数学拖网模型的计算结果，为了与试验值相比较，将数学模型网板间距设置为3.4 m，以保证相同的试验工况。由图8可以看出，两种数学模型的计算结果与模型试验结果相差不大，随着拖速的变化，袖端水平扩张均略有浮动，浮动程度较小。由图8可以看出，不同拖速下，计算值均较试验值小，但两者相差仅5%左右，说明数值模拟结果与水槽模型试验结果符合较好。

图8 试验与计算的袖端水平扩张比较Fig.8 Comparison of horizontal expansion of the end of net w ings between experiment and calculation

3 讨论

本文针对大网目底拖网建立了数学模型，提出了适用于拖网类渔具的网目群化方法。万荣等［10］和LIU等［19］认为在网目群化前后，需要网衣水中重量和投影面积相等以保证网箱网衣总体水动力相同。然而，材料密度的变化（文中分析密度是减小的）必然导致网衣体积增大，浮力增大，这在万荣等［10］的研究中并未考虑，原因可能是网箱下缘的重力足够大从而可以对浮力的增量忽略不计。但是，在拖网、张网等此类渔网具中，网身部分没有配重，需要对体积变化加以考虑，否则可能造成网衣整体浮力大于重力，出现网体上翘现象。

两种数值模型的网具阻力计算结果有一定差距，model-1计算值接近试验值，而model-2数值模拟的网具阻力较模型试验大16%～26%，但这与QUEIROLO等［20］发现数值模拟和物理模型试验结果之间存在差异（13%～23%）的结果相近，可能与群化后的数值模型网衣单元较少，虚拟单元长度较长有一定关系。两种群化模型在稳定流场中的形态变化趋势相近，特别是网口及网袖部分，网口垂直扩张和袖端间距结果相差较小，这说明大网目底拖网网身网目群化的程度对计算结果的影响可控，可依据试验条件适当减少网身部位的网衣单元，在保证一定精确率下提高计算效率。

在数值模型构建过程中，虚拟目脚单元最大长度达到514mm，同时选用的拖网网身网衣具有较多的工艺性挂目或并目，都在一定程度上对计算结果造成了影响，网衣在局部未达到理想的流线型状态，在今后的优化计算中需要加以分析和改进，以提高计算模拟的精度，更好的呈现拖网在流场中的状态。