铜合金编织网网片阻力水槽试验研究

王 磊,王鲁民,万 荣，刘永利,齐广瑞，宋 炜

(1中国水产科学研究院东海水产研究所，农业农村部东海与远洋渔业资源开发利用重点实验室,上海200090；2上海海洋大学海洋科学学院,上海 201306)

铜合金材料在海水环境中具有耐海水腐蚀，抗海洋污损生物附着等特性[1-2]。相比传统纤维网衣，铜合金网衣的特点使其在海水养殖网箱及养殖围栏上的应用发展迅速，其中铜合金编织网在大型柱桩式围栏上的应用具有一定代表性[3-4]。铜合金编织网是将铜合金线进行双向隔波弯曲，先轧后编而成的方孔平纹编织网，其互锁结构使网片结构较为稳定[5]。通过连接柱桩，铜合金编织网构成的围拦网可以经受较强浪流作用，且抗生物附着特性可以保持水体流通，降低鱼类病害发生率[6]。随着养殖设施装备的发展及深远海养殖的发展需求，大型养殖围栏作为一种可面向外海的养殖设施，其结构设计与安全性评估需要有更可靠的科学数据支撑，其中网衣的受力及强度设计是重要一环。常见的渔用网衣多为柔性网衣，众多学者通过水槽试验和数值模拟进行网衣的受力研究[7-14]。国内外学者也已开展过铜合金网衣的水动力性能等研究相关研究[15-19]，虽然铜合金网衣相比合成纤维网衣具备刚性的特点，但其研究方法和水动力衡量参数是基于柔性网衣的研究基础，也是通过水槽试验或数值模拟等研究方法，研究关注的内容主要是获得不同种类的铜合金网衣在水中的受力，及其与合成纤维网衣的受力性能对比等。

本研究通过开展铜合金编织网的水槽试验，获得可适用于养殖设施的多个规格铜合金编织网网片的水阻力数据，并结合数值曲线回归获得常用规格的铜合金编织网阻力值计算公式，同时基于试验数据初步分析获得网片的阻力系数与雷诺数的关系，为深远海大型围栏养殖设施的网衣受力计算及网衣水动力性能分析提供参考。

1 材料和方法

1.1 铜合金编织网

试验网片为铜合金编织网，选用系列规格直径和网目尺寸的铜合金线制成。网目为方形网目，网片及网目尺寸见图1。截取试验用网片尺寸均为500 mm×500 mm。

图1 铜合金编织网网片及网目尺寸Fig.1 The mesh size of copper alloy woven net

选用的铜合金线直径为2.5 mm、3.0 mm、3.5 mm、4.0 mm、4.5 mm和5.0 mm，由于金属制网机难以精准控制网目尺寸，以测量得到的网目尺寸为准，见表1，网片编号对应“线径-网目尺寸”。

表1 试验网片种类及规格表Tab.1 Main particulars of the net used in the test

1.2 试验概况

试验地点为中国水产科学研究院东海水产研究所静水池，水池主尺度：90 m(长)×6 m(宽)×3 m(深)。拖车速度精度：相对精度P≤1%。

试验网片安装于可旋转框架上，其旋转角度定位精度为0.01°。

本试验测力数据采集使用LSM-B-500NSA1-P型三分力传感器(量程500N)，试验模型安装示意图见图2。

图2 网片水槽试验安装示意图Fig.2 A sketch of experimental setup of nets in water tank

1.3 试验方法

1.3.1 试验数据测试方法

试验网片安装于不锈钢方形框架上，分别在流速v=0.30 m/s、0.45 m/s、0.60 m/s、0.75 m/s、0.85 m/s (水温15℃) 开展试验，其中冲角在0°～90°区间，每间隔10°为一个测录数据点，数据为阻力Fx和升力Fy。

图3 网片水动力性能试验参数定义示意图Fig.3 Definition of parameters related to net test in water tank

1.3.2 试验网片阻力与升力计算方法

在试验过程中，网片所在平面与水流(拖车前进)方向平行时定义冲角α为0°，三分力传感器随网片转动而同时转动，因此网片(带框架)的阻力为三分力传感器在水平面上的读数(Fx与Fy)沿流速方向的合力。

阻力：

Fnx=(Fx-Fkx)cosα+(Fy-Fky)sinα

(1)

升力：

Fny=(Fx-Fkx)sinα+(Fy-Fky)cosα

(2)

式中：Fx为网片与框架于三分力传感器X向的受力读数；Fy为网片与框架于三分力传感器Y向的受力读数；Fnx为网片阻力；Fny为网片升力；Fkx为框架于三分力传感器X向的受力读数；Fky为框架于三分力传感器Y向的受力读数；α为网片冲角，即网片所在平面与水流方向的夹角。

所有试验数据都进行了框架干扰修正，框架干扰修正是采用对应扣除框架(无网衣)的受力(Fkx和Fky)方法来完成。

1.3.3 铜合金网衣的阻力计算方法

渔用网具、网箱网衣及养殖围栏网衣等都是由网片拼接组成，拼接网片的材料和规格也不一定相同，而网衣的规格通常包含了网目尺寸、网线直径及网衣的编织型式。公式(3)是目前通用的平面网片阻力计算公式[20]：

R=ρSv2Cx/2

(3)

式中：R为阻力，N；ρ为水的密度，1 000 kg/m3；Cx为阻力系数，无量纲常数；S为特征面积，m2，v为流速，m/s。

由公式(3)，可得阻力系数Cx的计算公式：

Cx=2R/(Sρv2)

(4)

由于铜合金编织网与常见的合成纤维网特性不同，可以将铜合金编织网作为刚性体进行计算(水流作用下无形变)，铜线的直径可直接采用游标卡尺等测量。特征面积S即线面积，是构成网片的铜合金线投影面积，如规定网目总数Nm的矩形铜合金编织网，其构成网片的线面积Sk为：

Sk=Nm4ad

(5)

式中：a为网目尺寸(目脚长度)，m；d为网线直径，m。

18F-FDG PET/CT测量食管鳞癌病变长度及预测T、N及G分期的临床价值(王 菲)(5):429

为研究铜合金编织网各流速状态下雷诺数与阻力系数的关系，铜合金编织网的网平面与流速方向垂直时，可将网线作为圆柱体进行水动力分析，则雷诺数计算的特征长度为网线直径。

Re=ρdv/μ

(6)

式中：Re为雷诺数，无量纲常数；μ为水的动力黏滞系数，0.001 14 Pa·s。

2 结果与分析

2.1 结果

试验获得的数据经采用公式(1)和公式(2)处理后得到铜合金编织网网片的阻力Fnx和Fny，如表2的数据是编号4.0-40的网片在不同流速、不同流速冲角下的水阻力数据。

表2 铜合金编织网4.0-40网片阻力数据(N)Tab.2 Resistance data of net with a size 4.0-40 mm(N)

将试验获得各编号网片阻力数据进行归纳整理，并利用公式(3)～(5)进行计算，可以获得对应规格铜合金编织网的阻力系数，网片在与流速方向垂直(90°)时，铜合金编织网的线面积可采用公式(5)获得，表3数据是不同线径规格网片(网目尺寸50 mm)在90°冲角及对应流速下的阻力系数。

表3 铜合金编织网网片阻力系数CxTab.3 Drag coefficient of copper alloy woven net

2.2 分析

2.2.1 网片阻力与迎流冲角的关系

图4中Fnx-α曲线是由编号 4.0-40规格网片的阻力数据(表2)绘制的对应流速下网片阻力值与迎流冲角α的变化关系。由图可见，随着迎流冲角的增大，网片的阻力值也在增加，网片的迎流面积变化是造成网片阻力值变化的因素之一，网片的纬向(横向)铜线随着网片的转动(α角度变化)，使纬向的铜线迎流面积发生变化，同时由于铜合金编织网的铜线是波浪形结构(图1)，也造成了经向(竖向)铜线的迎流面积发生变化，故而网片阻力值也产生变化。

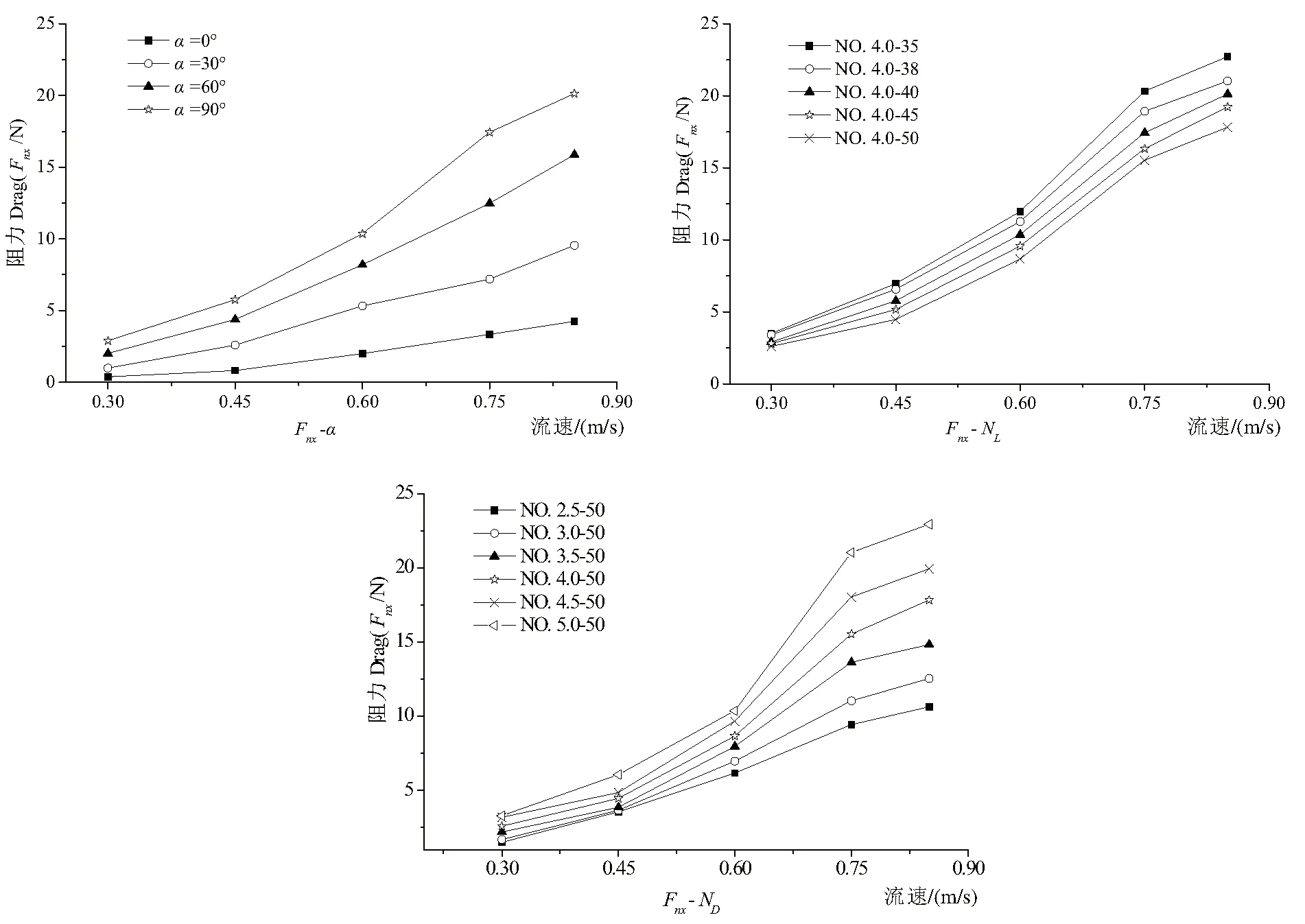
图4 网片阻力在不同流速下与网目尺寸、冲角、线径的关系Fig.4 The changing curve grouping comparison of net drag in several velocity along with the mesh size,angle of attack and wire diameter

图4中Fnx-NL曲线图是线径4.0对应5个规格网目尺寸的网片在水流冲角α=90°时的阻力数值随流速变化的曲线。由图4可见，不同规格网目尺寸的网片产生的Fnx-NL曲线趋势基本一致，阻力值随流速的增加而增大，同时由图中也可以看出在各对应流速下，阻力值与网目尺寸的变化关系，随着网目尺寸的增大，阻力值是降低的，这是因为网目尺寸增加使单位面积网片的网线数量减少，即网线的迎流面积减小，使阻力值降低。

2.2.3 网片阻力与铜线线径的关系

图4中Fnx-ND曲线图是选取网目测得的网片阻力值曲线。由图4可见，随着铜线线径的增加，网片的阻力值是增加的，网目尺寸不变，表示每个规格铜线线径网片的铜线长度相同，由于线径的变化造成网片迎流面积的变化，这是网片阻力值变化的主要原因。

2.2.4 网片阻力系数与雷诺数的关系

雷诺数Re是研究网片水动力性质的一个重要参数，是流速及特征长度的函数，由公式(6)可知，铜线线径是网片雷诺数的特征长度，将雷诺数Re及网片的阻力系数Cx进行分析，两者的变化关系是网片水动力性能研究的重要指标[21]。通过公式(6)计算6种线径铜合金编织网在网片平面垂直流速方向、网片平面平行流速方向，不同流速下的雷诺数，并结合表3本试验数据绘制雷诺数Re与阻力系数Cx的点状图，见图5。

图5 网片阻力系数与雷诺数的关系Fig.5 The relationship between the drag coefficient and the Reynolds number of the mesh

基于点状图采用幂函数回归，得到雷诺数Re与阻力系数Cx的关系公式(7)和(8)。

Cx90=1.690 5Re-0.032

(7)

Cx0=0.003 4Re0.5638

(8)

公式(7)和(8)中：雷诺数Re范围为658～3 727；Cx90为网片平面垂直于流速方向的阻力系数，范围为1.12～1.65；Cx0为网片平面平行于流速方向的阻力系数，范围为0.08～0.34。

3 讨论

3.1 不同规格网衣的阻力

单位面积的网片，增大网目尺寸和降低网线直径，都会使线面积减小，水阻力降低。

陈昌平等[19]通过水槽试验和数值模拟的方法，对3种规格目脚长度和3种规格网线直径的金属网片进行了网衣受力研究，研究也表明随着网线直径的增大，网衣受力增加，随着目脚尺寸的增大，网衣受到的水阻力值减小，其变化趋势与本研究一致。

基于本试验系列规格铜合金编织网的试验数据，利用多项式回归可以得到不同规格网片随流速的变化曲线，公式(9)～(18)是本试验10种规格网片(线径-网目尺寸)在冲角90°时单位面积(1 m2)网片随流速变化的受力公式：

网片规格2.5-50：F=62.896v1.916 7

(R2=0.987)

(9)

网片规格3.0-50：F=73.684v1.982 4

(R2=0.988)

10)

网片规格3.5-50：F=85.400v1.952 5

(R2=0.977)

(11)

网片规格4.0-50：F=97.940v1.943 7

(R2=0.985)

(12)

网片规格4.5-50：F=107.900v1.883 1

(R2=0.974)

(13)

网片规格5.0-50：F=127.176v1.952 7

(R2=0.969)

(14)

网片规格4.0-35：F=127.576v1.857 3

(R2=0.987)

(15)

网片规格4.0-38：F=117.168v1.814 1

(R2=0.986)

(16)

网片规格4.0-40：F=112.828v1.918 8

(R2=0.992)

(17)

网片规格4.0-45：F=105.304v1.916 0

(R2=0.992)

(18)

式中：F为水流冲角90°时网片单位面积的水阻力，N/m2；v为水流速度，m/s；R2为拟合优度。该系列公式可为本试验涉及规格铜合金编织网在不同流速下的水阻力计算提供计算依据。

3.2 网片阻力与冲角

渔具型式及养殖设施网体形状决定了网衣在使用时是与水流成多角度的，因此网衣与水流冲角的关系是网衣水动力研究的重要内容[22-25]。渔网与网箱使用的网衣多为柔性纤维网衣，因此关于平面网片的阻力研究多以柔性网衣为对象，如詹杰民等[26]基于流体力学试验，研究了流向对平面合成纤维网衣受力的影响，认为当网片与流向垂直时阻力值最大，随着网片平面与流向的角度逐渐减小其阻力值降低。

铜合金编织网在水流作用下，因其金属特性不易产生拉伸变形，故其阻力研究方法自适应于已有的网片水动力研究理论。图6是铜合金编织网4.0-40在各试验流速下，网片阻力和阻力系数与冲角的关系，可见，该关系变化趋势与詹杰民等[22]利用柔性纤维网衣的流体力学试验结论相一致。

图6 网片阻力及阻力系数与冲角的关系Fig.6 The relationship between the net drag and drag coefficient and the angle of attack

现有的研究表明，当网衣平面与水流角度发生变化后，网片的水阻力变化是与网线在垂直流向平面的投影面积有直接关系[27]，由公式(5)，即其特征面积S是在垂直流速平面上构成网线的铜合金线投影面积Sk，该面积值与流速冲角有关系，冲角越小，Sk越小，因此网衣的水阻力也越小。陈天华等[28]采用计算机模拟方法研究了桩柱式围网单元柔性网衣的受力，研究表明网线的最大张力值随冲角的增大而增大，其变化趋势与网片投影面积随角度的变化相似。

参照列维恩平面网片阻力理论假说[20]，网片平面与流速成一定角度时的阻力和阻力系数的计算公式为：

Rα=RD0+(RN90-RD0)sinα

(19)

Cα=CD0+(CN90-CD0)sinα

(20)

在公式(19)和(20)中，RD0、RN90分别为网片与流速垂直和平行时的阻力；CD0、CN90分别为网片与流速垂直和平行时的阻力；Rα、Cα分别为网片与流速成α角度时的阻力和阻力系数；α为网片平面与流速夹角。

图6中网片的阻力系数随冲角的变化趋势基本一致，与田内、今井健彦、克鲁和列维恩等[20]提出的在各种角度下的研究结论相一致。基于公式(20)及图6中的Cx—α曲线，经数据拟合，铜合金编织网4.0-40在不同冲角下的阻力系数计算公式中，CD0为0.21，CN90为1.20，与田内公式接近(CD0=0.27，CN90=1.1)。

3.3 铜合金编织网水动力性能

铜合金编织网由于其结构特性，在流体中的水动力性能即具有单柱体流体特性，又具有网形状的流态叠加影响特性，尤其波纹状的网线结构，使网衣在不同冲角下的微观受力分析更为复杂。由本试验数据得出的阻力计算公式(8)～(17)看出，在阻力与速度幂函数的关系中，速度的幂值范围均小于2，这表示流态没有处于自动模型区，尚处于低雷诺数的流态转换区[20]，对于铜合金编织网养殖设施的模型试验研究，需要参考网衣受力的模型试验准则[29]。

铜合金编织网的结构与材料特性，也直接影响了其水动力性能，Tsukrov 等[17]采用水槽试验方法对铜合金编织网、尼龙网、铜合金斜方网等数种网衣进行水动力性能分析比较，结论认为铜合金编织网的阻力系数(网衣平面垂直流速)相比合成纤维网衣较低，但相比铜合金斜方网等金属网的阻力系数较高；这是因为铜合金斜方网的网线没有铜合金编织网的波纹铜线结构，结构较为简单。

铜合金编织网的水动力计算，通常是基于平面网片的水动力分析理论，通过大量的试验数据建立网片阻力计算经验公式，如国外学者弗里特曼、田内等[20]，国内学者虞聪达等[30]都是基于大量水槽试验，结合理论分析提出网片水阻力计算的经验公式。本研究基于试验数据，推导得出以公式(7)和(8)为代表结论的铜合金编织网的网衣阻力系数与雷诺数的对应关系，该公式结合公式(20)可用于推导处于本试验雷诺数范围内的网衣阻力系数。

4 结论

网片的阻力在固定水流冲角下是随着流速的增加而增大，同时在特定流速下，网片的阻力随着水流冲角的增加而增大(冲角90°为网片平面与水流垂直)，并根据数据曲线回归得到在冲角90°时单位面积系列规格铜合金编织网随流速变化的水阻力计算公式；通过网片阻力与网片规格及冲角变化的分析，认为网片阻力与网片的特征面积有直接关系，即特定流速下，铜合金编织网的铜线在与水流垂直平面的线面积投影越大，则其阻力值越高；基于试验数据分析了铜合金编织网阻力和阻力系数随冲角的变化情况，雷诺数与阻力系数的关系等，并结合相关经验公式给出了铜合金编织网阻力系数的计算公式。本研究结果可以为铜合金编织网的水阻力计算及水动力性能分析提供参考。

□