蟹塘投饲船螺旋驱动装置设计与水动力性能分析

陈雷雷，任万川，李 俊，张丽珍，胡庆松

(上海海洋大学工程学院，上海 201306)

水产养殖过程中使用投饲船进行投饲作业是实现养殖集约化和规模化的前提与保障[1]，同时投饲船的应用也有助于提高饲料投喂效率，而高效的投喂策略能够提高养殖对象的存活率和生长性能[2]。河蟹池塘养殖一般采用种草养蟹模式，为了使河蟹有更好的生长环境，蟹塘水草种植覆盖率一般高达60%以上[3-5]。当前以明轮与螺旋桨为驱动装置的投饲船不能适应水草密集蟹塘的投饲作业，因此，针对蟹塘投饲作业，适应多水草环境的驱动装置研究显得十分必要和迫切。

近年来为了减轻水草对投饲船投饲作业的影响，人们针对投饲船进行了优化研究。李俊等[6]将双体投饲船的船底设计为圆棱形状以有效减少水草对船体的阻力，改变船型虽然降低了投饲船在多草水环境中的行驶难度，但无法避免其驱动螺旋桨被水草缠绕。应对此问题，孙月平等[7]以空气螺旋桨为驱动，虽然避免了水草缠绕，但动力不足、行驶速度较慢、且无法通过水草密厚区域。而螺旋驱动装置常用于雪地、沼泽与泥地等路面松软且路况复杂的应用环境[8-9]，具有很好的多草水环境适应能力。螺旋驱动装置在农业领域的创新应用是当前的研究热点之一。冯闯闯等[10]设计了一种螺旋推进式挖藕机，并对其在藕田的行驶滑转率进行分析，为水田行走装备的研究提供了经验；靳航嘉等[11]针对粮面承压能力与抗剪切强度低的难点，提出了一种螺旋驱动式粮仓机器人行走机构，解决了机构在粮面行走时易下陷打滑的问题，分析了滑转率、沉陷量与转速的关系，为粮面行走机构的研究提供了参考。赵玉凡等[12]基于螺旋驱动器建立数学模型，证明任意滑转率的螺旋叶片均不产生推土现象。樊启洲等[13]做了类似的工作，同时推导了螺旋驱动器的黏附-摩擦阻力计算公式。郭晓林等[14-15]对螺旋驱动装置进行了土质环境中动力学仿真分析，得到了随滑转率与螺旋出土角增大，推进力也随之增大的结论，并对螺旋驱动装置转向过程中滑移、滑转现象进行了探索。Dugoff等[16]通过螺旋推进车模型，研究了螺旋推进车结构参数、负载、速度与车辆牵引力和滑转率的关系。Nagaoka等[17]利用车辆地面力学理论建立了数学模型，同时通过仿真分析了松软地面的土壤剪切力和应力轨迹。可见螺旋驱动装置在土质地面，松软地面及颗粒堆积表面等应用环境都具有优越性能，以上研究也在这些方面取得了较好的成效。

综上，蟹塘投饲船设计中采用螺旋驱动装置，要求螺旋驱动装置具有水草适应能力的同时具备优越的水动力性能是蟹塘作业的重要前提，但是，当前关于螺旋驱动装置的水动力性能研究探索较少。本研究从蟹塘投饲需求和蟹塘投饲船的总体结构出发，探讨了基于计算流体力学(computational fluid dynamics，CFD)方法的螺旋驱动装置的水动力性能分析方法，通过对螺旋驱动装置螺旋叶片的螺距与叶片高度的研究，确定了驱动装置的水动力性能与螺旋叶片的关系，为螺旋驱动装置在水体环境中的应用研究提供参考。

1 螺旋驱动装置设计

1.1 整体模型设计

河蟹养殖中出于增加溶氧、提供植物性饲料等原因，大面积种植水草[18-19]，加之河蟹养殖对水质要求较高，集中投喂产生的剩余饲料会污染水质[20-21]，这就要求蟹塘投饲船具有水草区域行走与全塘均匀投喂饲料的能力。螺旋驱动的蟹塘投饲船由图1所示的饲料箱、抛料盘、连接机构、支撑机构和螺旋驱动装置5个部分组成。

图1 螺旋驱动投饲船三维模型图Fig.1 3D model of spiral driven feeding boat

饲料箱用于装载饲料，底部的漏斗结构保证均匀完整下料；抛料盘进料口与饲料箱下料口竖直对齐，通过控制器控制饲料箱抖动下料，利用抛料盘的离心力将饲料呈扇形抛撒，确保饲料均匀分布；连接机构与驱动装置组成投饲船的动力系统，呈锥台结构，锥台一侧走线通道用以电机与电源的连接；支撑机构用于连接投饲机构和动力系统；螺旋驱动装置工作时绕两锥台连接的中轴旋转，产生浮力与推进力。

1.2 螺旋驱动装置设计

螺旋驱动装置为投饲船提供浮力与推进力，作为核心动力装置，螺旋驱动装置在水体环境的工作原理具体表现为：外侧驱动装置以角速度ωi转动、内侧以角速度ωj转动时，驱动装置为差速运行状态，控制电机转速大小可实现不同角度转向，其中转向半径与转向角速度根据文献[15]表达式如公式(1)～(3)所示。驱动装置旋转方向决定蟹塘投饲船行驶方向，当驱动装置相向转动时控制纵向的前进与后退，同向转动时控制蟹塘投饲船横向的进退，且行驶方向与转向一致。

Δω=ωi-ωj

(1)

k=ωj/ωi

(2)

(3)

式中：Δω表示内外侧驱动装置角速度差，rad/s；k表示内外侧驱动装置转动角速度比值；l表示驱动装置中心轴的轴距，m；P表示螺旋叶片螺距，m；RT表示转向半径，m；ωT表示转向角速度，rad/s。

螺旋驱动装置在水体中的行驶效果与结构参数相关，针对不同的应用环境进行结构参数调整，蟹塘投饲船的螺旋驱动装置结构参数示意图如图2所示，由一个中空圆筒与缠绕在圆筒上的两条交错螺旋叶片组成，螺旋叶片高dl、厚ds，有效长度为L，它与螺距的关系根据文献[22]可表达为：

图2 螺旋驱动装置结构参数示意图Fig.2 Schematic diagram of structure parameters ofscrew drive device

L=N·P

(4)

式中：L表示螺旋叶片有效长度，mm；N表示螺旋叶片数量；P表示螺旋叶片螺距，mm。

螺旋叶片N的数量通常选择在2～3片，这里选择N=2。螺旋驱动装置的直径为浮筒直径dm与叶片高度dl之和，表示为：

D=dm+2dl

(5)

式中：D表示螺旋驱动装置直径，mm；dm表示浮筒直径，mm；dl表示叶片高度，mm。

圆筒上的两螺旋叶片螺距相同，螺距P与叶片间隙δ的大小成正比，螺距P与螺旋升角η的数学关系表达为[23]：

P=π(D+dl)tanη

(6)

式中：P表示螺旋叶片螺距，mm；D表示螺旋驱动装置直径，mm；dl表示叶片高度，mm；η表示螺旋升角，(°)。

(7)

(8)

F=ρ水Vg

(9)

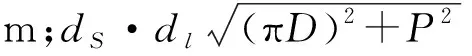
河蟹池塘养殖过程中，河蟹苗种的放养规格一般为150～200只/kg，每亩放养数量在650～700只范围间，其饲料投喂需根据“两头精，中间青”投喂原则，即春秋主要以动物饲料为主，夏季投喂植物性饲料。饲料的投喂还基于天气、摄食活动强弱以及河蟹自重等条件进行调整性投饲[25-26]，因此，蟹塘投饲船应兼具投饲量可调性和应用便利性。根据表1可知船体自重为12.1 kg，考虑到投饲所需载重量与蟹塘投饲船的安全余量，两驱动装置应具有40 kg载重量，根据公式(7)～(9)可以算出浮筒体积应为0.02 m3。由于驱动装置的浮力主要由浮筒提供，螺旋叶片所提供浮力可忽略不计，浮筒直径Dm和螺旋叶片有效长度L可根据所需外观设计基于浮力需求做出调整。为了整体美观，驱动装置有效长度L为660 mm，浮筒直径为200 mm。

表1 船体组成及质量Tab.1 Hull composition and mass

2 螺旋驱动装置计算模型构建

2.1 计算域与网格划分

螺旋驱动装置的计算域分为静止域与旋转域，其中旋转域采用运动坐标系，旋转域在静止域中以一定转速转动。螺旋驱动装置直径为D，为了准确模拟螺旋驱动装置的流场分布情况，将计算域大小设置如下：静止域直径为5D，旋转域前端与入口距离设置为4D，旋转域后端与出口距离为15D，旋转域直径为1.2D，长度设置为驱动装置长度的1.2倍。完成驱动装置的计算域设置后进行网格划分，网格划分情况决定数值模拟的准确性[27-28]。为了对比验证粗网格划分、分区划分与细网格划分方式的计算速率以及计算的准确性，进行了网格无关性验证，如表2所示。

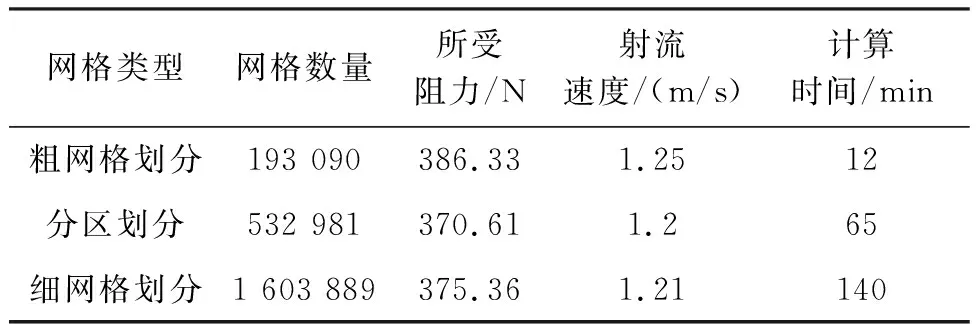
表2 网格无关性验证Tab.2 Meshes independence verification

根据表2数据，在权衡了仿真效率与准确性的情况下，螺旋驱动装置计算域应采用分区划分。将结构复杂且对网格质量要求高的螺旋驱动装置采用单元网格为0.014D的细网格划分，旋转域使用单元网格大小为0.3D的中等网格，静止域为驱动装置流场，对网格质量的要求不高，因此采用粗网格划分，单元网格为1.2D。分区划分完成后网格数量在500 000～550 000间，网格的整体划分如图3所示。

图3 计算域的网格划分Fig.3 Calculation domain meshing

2.2 流动控制方程与湍流模型

螺旋驱动装置绕纵向轴轴向在近似匀速的水体中做旋转运动，RANS方程是黏性流体运动学和动力学的普适性控制方程[29]，水作为不可压缩黏性流体，可采用平均雷诺(Reynolds-averaged Navier-Stokes，RANS)方程，驱动装置在流场中的连续方程与运动方程表达式如下：

(10)

(11)

(12)

( 13 )

2.3 边界条件设置

CFD仿真求解器时间选择稳态，设置新增流体材料水(water-liquid (h2o))，密度998.2 kg/m3。在螺旋驱动装置的计算域中，旋转域与静止域之间互不干扰，故旋转域选择运动坐标参考系，旋转域的旋转速度给定为600 r/min。将计算域的入口inlet的入口条件设置为速度入口(velocity-inlet)，出口outlet设置为压力出口(pressure-outlet)，将螺旋驱动装置壁面条件设置为可滑移的旋转壁面。

3 螺旋驱动装置水动力性能分析

3.1 计算模型具体参数

为研究螺旋叶片高度与螺距对驱动装置水动力性能的影响，使用SolidWorks建立驱动装置三维模型，对其螺旋叶片的高度与螺距进行流体仿真分析。螺旋驱动装置模型的浮筒直径均为200 mm，螺旋叶片厚度为16 mm，有效长度640 mm。螺旋叶片高度仿真试验组建立32个计算模型，螺距为255 mm、284 mm、320 mm以及366 mm，每个螺距均对应叶片高度dl在44～72 mm，步长为4 mm。在获取了范围44～72 mm内水动力性能较好的叶片高度前提下，保持叶片有效长度不变，建立范围在213～512 mm内的8组不同螺距的螺旋驱动装置计算模型，每组螺距以0.25螺旋叶片圈数为步长，且为了保持驱动装置的美观性，对每个螺距做出了1～5 mm的调整。

3.2 不同叶片高度下的水动力性能

以叶片高度试验组进行水动力仿真分析，根据射流速度结果绘制的趋势线如图4所示。螺旋叶片的高度在44～60 mm范围内时，射流速度随叶片高度上升而递增，且在44～64 mm区间内60 mm处的射流速度为最大值。64 mm之后螺旋驱动装置射流速度继续呈上升趋势，整体趋势上，除去60 mm处的射流速度在44～64 mm范围内增长值较大，螺旋驱动装置射流速度随叶片高度增加而递增。

图4 不同叶片高度下的射流速度Fig.4 Jet velocity at different blade heights

根据叶片高度仿真试验组的模拟计算，8个叶片高度下螺旋驱动装置所受阻力趋势线如图5，所受阻力在44～56 mm与64～72 mm区间内随螺旋叶片长度变大而增加，从总体的增长趋势观察，驱动装置受到的阻力与叶片高度的增加成正比，斜率范围在8～10.6之间。

图5 不同叶片高度下的阻力Fig.5 Resistance at different blade heights

由叶片高度的射流速度与所受阻力的趋势线分析，叶片高度在44 mm时的射流速度与所受阻力最小，为了分析驱动装置在叶片高度44～72 mm范围内水动力性能，以44 mm螺旋叶片高度为基准值，计算其余叶片高度相对于44 mm处的3个增长率——射流速度增长率、所受阻力增长率、增长率比值C。其中增长率比值C为：

(14)

式中：C表示增长率比值；Gr1表示射流速度增长率；Gr2表示所受阻力增长率。

增长率比值越大，相对44 mm所提高的水动力性能越大，具体数据如3所示。

分析表3中数据，60 mm处射流速度增长率增幅较大，所受阻力增长率增幅较小，此外随着叶片高度的增加，射流速度增长率与所受阻力增长率随之递增。由于分子分母均为增长趋势，增长率比值C的数值增长呈现非线性。同时在48～72 mm叶片高度范围内，以44 mm叶片高度为参考值，C在叶片高度取60mm时总能达到最大值，水动力性能增长幅度较大。叶片高度60 mm下的螺旋驱动装置流线分布截面图如图6。

表3 同一螺距下不同叶片高度的增长率及增长率比值

图6 叶片高度60mm下的螺旋驱动轮流线分布截面图Fig.6 Section diagram of streamline distribution of helical drive device at blade height of 60 mm

3.3 不同螺距下的水动力性能

叶片高度试验组的计算分析验证了44～72 mm范围内取60 mm时水动力增幅较大，因此保持叶片高度为60 mm，对螺距范围在213～512 mm的8个驱动装置模型进行计算分析。如图7所示，观察不同螺距下射流速度的趋势线可知，螺旋驱动装置射流速度与螺距无明显的线性关系。根据图8中所受阻力的趋势线，所受阻力与螺距成正比，斜率为1.65且R平方值为0.98，趋势线拟合度高。

图7 不同螺距下射流速度Fig.7 Jet velocity at different pitch

图8 不同螺距下所受阻力Fig.8 Resistance at different pitch

由于螺距与射流速度没有明显的线性关系，为研究螺距在213～512mm范围内驱动装置水动力性能的增长情况，将螺距为195 mm时的射流速度与所受阻力拟作为基准值，以此计算该范围螺距下的增长率比值C，C越大水动力性能提升越明显。根据表4数据，驱动装置的增长率比值在螺距255 mm处取最大值0.25，驱动装置在此处的水动力性能增长幅度较大。不同螺距下的流场分布情况如图9所示。

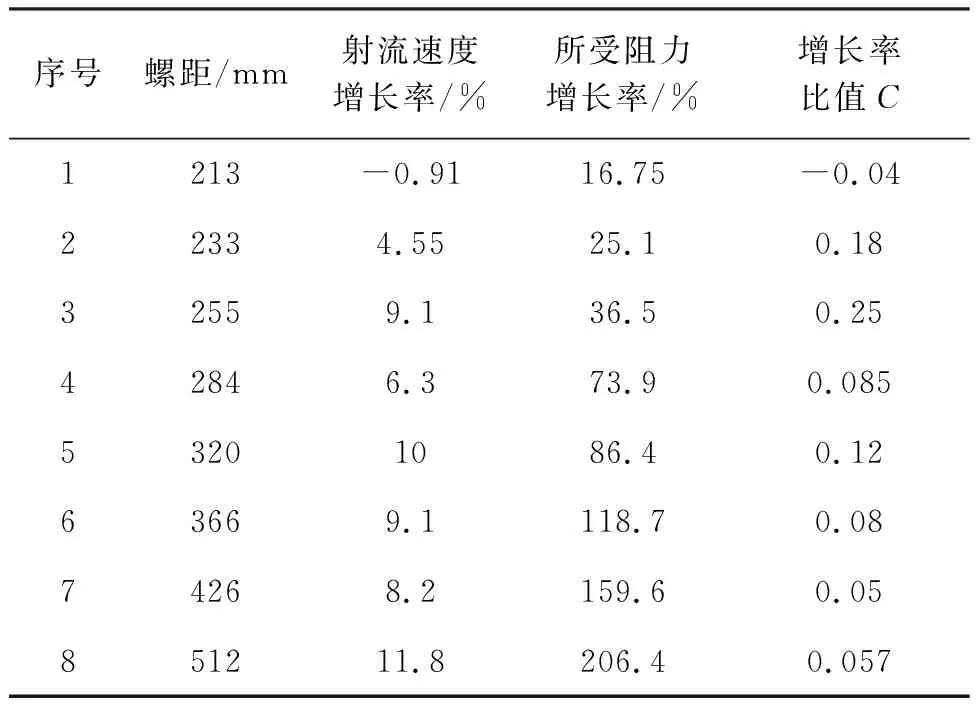
表4 60mm叶片高度下不同螺距的增长率比值Tab.4 Growth rate ratio of different pitch at 60 mm blade height

图9 不同螺距下的流线截面图Fig.9 Streamline section diagram at different pitch

4 小型样机试验验证

4.1 小型样机试验

为验证螺旋驱动装置在水中的行驶状况，采用1∶4的比例设计了一台重2 kg的小型样机，其驱动装置的浮筒直径50 mm，长为165 mm，螺旋叶片螺距90 mm，叶片高6 mm，如图10a所示。小型样机驱动装置内部中空，将驱动电机放置于驱动装置内部，以缩小重心与形心的距离。驱动装置中的驱动电机设有防水措施，样机前端的锥形结构有助于减小所受阻力。

试验场地选择在上海海洋大学人工湖，进行小型样机螺旋驱动装置在水中的阻力试验，如图10b所示。在满速条件下使用拉力计测量所受阻力，重复测量15次，取试验所测阻力平均值为2.33 N。

图10 小型样机水上阻力测试试验Fig.10 Small prototype water resistance test experiment

4.2 小型样机数值模拟与对比验证

为确保驱动装置螺旋叶片参数与水动力性能的关系具有普适性，同时验证数值模拟结果的准确性，基于小型样机参数，分别就63.5、70、80和90 mm 4个螺距，建立螺旋叶片高度为6～20 mm的36个驱动装置计算模型，以仿真结果绘制趋势线。根据图11射流速度趋势线，P70与P80在叶片高度为6～20 mm范围内射流速度随叶片高度的增加而递增，P63.5与P90总体也呈增长趋势。图12中驱动装置所受阻力在6～20 mm范围内与叶片高度成正比。两趋势线的R平方值均在0.98以上，具有较高的拟合度。驱动装置的螺旋叶片参数与水动力性能关系具有普适性。

图11 射流速度趋势线Fig.11 Jet velocity trend line

图12 所受阻力趋势线Fig.12 The resistance trend line

螺旋驱动装置的1∶1计算模型的阻力计算结果为1.22 N，由于样机所测为两个驱动装置所受阻力，将水面试验所测阻力除2得1.165 N，对比可知误差为4.72%。参照文献[33]在三叶螺旋桨水动力性能分析中仿真与试验的误差控制在6%，本研究数值模拟结果与试验结果误差在5%以内在可接受范围内，证明了螺旋驱动装置的水动力计算模型具有可行性。

5 结论

为了实现河蟹池塘的全塘均匀投喂，设计了一种能行驶于水草环境的蟹塘投饲船，并根据投饲需求对螺旋驱动装置参数进行设计。在此基础上，为研究螺旋驱动装置叶片参数与水动力性能之间的关系，针对螺旋叶片构建了44～72 mm范围的高度试验组与213～512 mm范围的螺距试验组，以Ansys fluent为平台，采用控制变量法，对两试验组计算模型进行数值模拟计算。射流速度试验表明射流速度随叶片高度上升递增而螺距与射流速度无线性关系。阻力试验表明，螺旋叶片的高度与所受阻力成正比，趋势线斜率在8～10.6之间，叶片螺距与所受阻力成正比，斜率为1.65。综合考虑了两个参数，驱动装置螺旋叶片的叶片高为60 mm且螺距为255 mm时，其水动力性能表现较为优异。同时，小型样机试验与对比分析结果显示仿真模型与物理模型试验误差为4.72%，小于5%，验证了所提出的螺旋驱动装置水动力仿真分析方法的可行性与可靠性。

□