基于双线性基函数磁场积分方法的研究

万心悦， 蒋年德， 刘耀成， 吴聪平

(1.东华理工大学 长江学院，江西 抚州 344000；2.东华理工大学 信息工程学院，江西 南昌 330013)

分析三维目标的电磁散射问题，最常用的方法是通过应用三角形离散散射面，即矩量法。通常用平面RWG基函数来定义平面三角形，描述公共边上的电流，从而扩大未知表面的电流密度。但RWG基函数只是零阶完备的，并且具有低阶收敛特性，即使减小剖分尺寸，增加未知量，对求解结果的精确度提高效果甚微(罗晨等，2019；董洪鹏，2017；王晶晶，2019)。

由于矩量法是通过使用三角形离散目标表面，将目标结构的散射问题转换成电场积分方程或磁场积分方程进行计算。这两组方程中的电流分布定义虽然是相同的，但是研究发现磁场积分方程计算所得结果的精度低于电场积分方程，尤其当目标物体的几何形状是曲面或尖锐的情况时，其精确性会更差(朱武兵等，2018；吴小川，2010；阙肖峰等，2008)。

为解决这一问题，笔者将双线性基函数应用于磁场积分方程，对曲面结构和尖锐结构的散射特性进行分析和计算，以期获得更高的精确度(赵庆广等，2014；Levent et al., 2009)。

1 基于双线性基函数的磁场积分方程

1.1 双线性基函数

双线性基函数是通过提供6个自由变量来描述在三角形线上线性变化的向量，其是一阶完备的，因此在这一特性上优于RWG基函数。如图1所示，在公共边上定义两个不同的L-L基函数以扩大电流密度，这比使用零阶完备的RWG基函数精确度更好。在不改变剖分三角形的情况下，与RWG基函数相比，双线性基函数只是花费了基函数数目增加一倍的成本来实现高阶完备性，从而改进RWG的建模(罗春备，2019)。

图1 第一类(a)和第二类(b)L-L基函数

第一类L-L基函数和第二类L-L基函数都定义在公共边em上，箭头显示二者方向不同，阴影的深浅代表矢量大小的分布。浅色和深色部分分别代表数值小和数值大，白色代表数值为零。两类L-L基函数的表达式分别为:

(1)

(2)

事实上，在一公共边上的两类L-L基函数之和就是常用的RWG基函数：

(3)

散度的表达式:

(4)

由式(4)可见，两类L-L基函数的散度是相同的，并且完全等于RWG在基函数的一半。因此L-L基函数的实现可在原RWG基函数的代码上做简单的修改，例如近场作用奇异点提取和远场作用傅里叶变换，都可以在采用RWG基函数代码的基础上改编。另外，对于相同数量的未知数，与RWG基函数相比，L-L基函数在实现中不要求额外的计算量(He et al., 2014, 2016；Ding et al., 2014； Zhang et al., 2015)。

1.2 磁场积分方程阻抗元素的填充

理想导体磁场积分方程为

en×[Hs(r)+Hi(r)]=J(r),r∈S

(5)

其中en为导体外法向方向上的单位矢量；Hs为散射场；Hi为入射场。散射场与表面感应电流的关系为

(6)

因此，方程可化为

=en×Hi(r),r∈S

(7)

未知的电流函数是一个矢量函数，因此用L-L基函数展开为：

(8)

将式(8)带入(5)式，得：

(9)

应用Galerkin方法测试积分方程式(9)，得到：

Zq·I=Vq

(10)

用矩阵方程表示，其中：

(11)

可见应用L-L基函数所构造的阻抗矩阵扩展了RWG基函数的阻抗矩阵，由m×n变为2m×2n(陈廷蓉，2018)。

1.3 近奇异性的处理

RWG基函数的电场和磁场积分方程的两种积分形式：

(12)

(13)

式(12)与式(13)中St表示三角形表面。假设一个转换坐标系，使三角形在x-y平面上，法向向量在z方向上。对于上式中积分数值的计算，可以通过提取奇异值使积分形式变为：

(14)

式中，R=|r-r′|。等式(14)右边第二项可获得解析解，因为有：

(15)

对于式(13)中积分数值的计算，可以通过提取奇异值使得积分形式变为：

(16)

因为有：

(17)

(18)

2 仿真及结果分析

算例一：导体球模型

此算例为自由空间中的导体模型，其表面为曲面，半径为1 m，入射波的频率为300 MHz，入射角为0°，极化方式为θθ极化，散射角为0°到180°。使用ansys软件对导体球表面进行离散，离散尺寸为0.1 m，剖分后得到三角形内边数共为3 852，则计算未知量为3 852，使用L-L基函数离散未知电流，未知量等于三角形内边数的两倍，即7 704。

图2为采用RWG基函数和L-L基函数的磁场积分方程分别计算出的自由空间中导体球的双站RCS。与Mie级数的结果比较，二者与Mie级数吻合很好，准确度很高，但在散射角度150°到180°的区域L-L基函数的结果精确度更高。

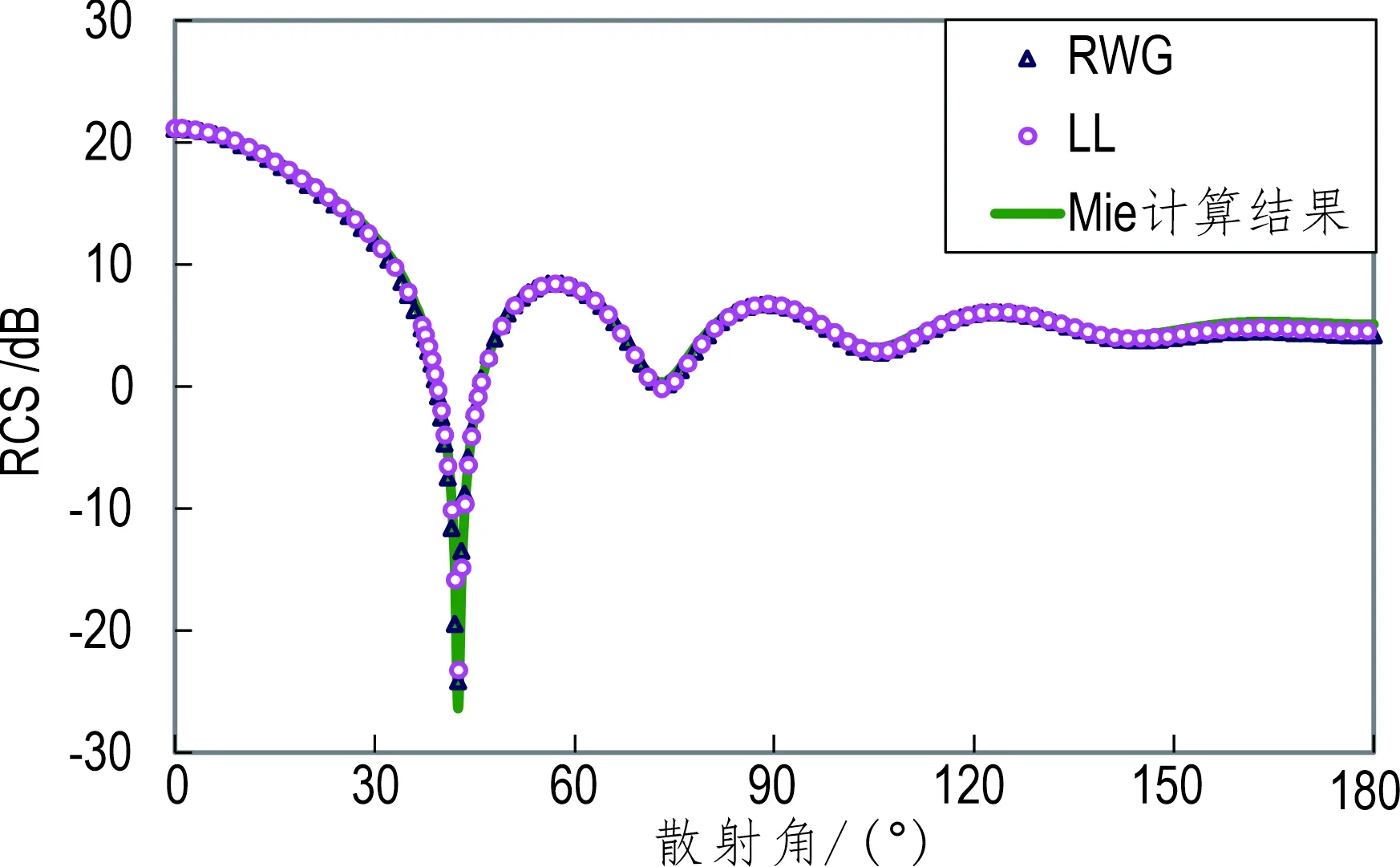
图2 导体球模型的双站RCS

为了更直观地反映双线性基函数的优势，图3给出了散射角150°到180°计算结果的误差对比。由此可见双线性基函数有效提高了磁场积分方程的精确度。

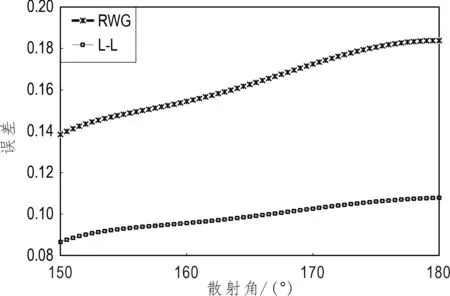
图3 两种基函数在散射角150°到180°范围下的计算误差比较

算例二： 导体立方体模型

此算例为自由空间中导体模型，有八个尖锐结构，其中立方体边长为1 m。入射平面波的频率为300 MHz，入射角为0°，极化方式为θθ极化，散射角为0°到180°。对导体表面进行三角形网格离散，剖分尺寸为0.1 m，剖分后得到三角形内边数为1 998，使用RWG基函数离散未知电流，未知量等于三角形内边数1 998，而使用L-L基函数离散未知电流，未知量等于三角形内边数的两倍，即3 996。图4为分别使用RWG基函数与使用L-L基函数的磁场积分方程所计算出的导体立方体的双站RCS，与FEKO仿真结果比较，使用L-L基函数计算所得结果的精确度更优。

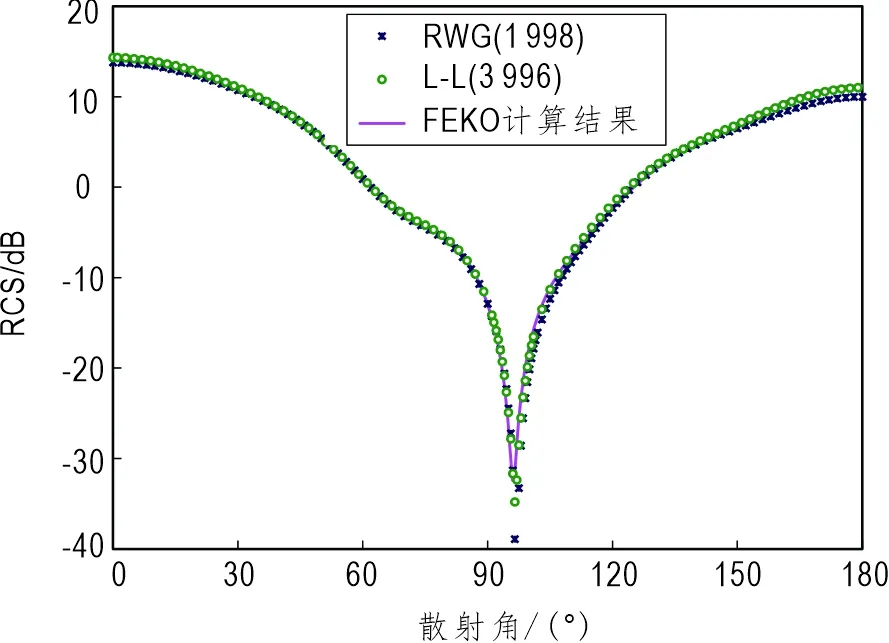
图4 导体立方体的双站RCS

虽然RWG和L-L基函数在对目标结构进行剖分时采用了相同的剖分尺寸，但L-L基函数所造成的未知量是RWG基函数的两倍，为了不额外增加计算量，笔者分别对模型采用不同尺寸的剖分。

图5为RWG基函数和L-L基函数在不同剖分尺寸下的计算结果。结果显示，L-L基函数在与RWG基函数保持相似未知量的情况下，仍能得到更加精确的结果。

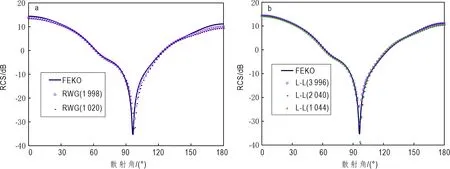
图5 两种基函数不同剖分尺寸与FEKO计算结果比较

为了进一步更直观地看出L-L基函数的优势所在，对RWG基函数和L-L基函数不同未知量求解结果的细节误差进行了对比(图6)。在相同等级未知量的情况下，L-L基函数能够获得更加精确的结果。

图6 不同散射角范围下RWG基函数与L-L基函数的计算误差比较

3 结论

针对在计算目标电磁散射时使用RWG基函数填充所造成的磁场积分方程精度不高的现象，提出了使用L-L基函数对磁场积分方程进行填充。该基函数通过在公共边上定义一对不同的函数以扩大电流密度，从而实现高阶完备性，改进RWG的建模。本研究推导了双线性基函数填充磁场积分方程的矩阵阻抗元素并采用奇异值提取法进行处理，进而对目标结构的双站RCS进行计算和分析。实验结果表明，L-L基函数能够在保证计算量不增加的情况下，有效提高磁场积分方程计算曲面及尖锐目标散射结果的精确度。