基于能量限制的分布式无线传感器网络调度

卫朝霞，刘志超，罗 佳

(1.四川大学锦城学院，四川 成都 611731；2.无锡太湖学院物联网工程学院，江苏 无锡 214064；3.江南大学物联网工程学院，江苏 无锡 214122；4.四川大学锦江学院，四川 彭山 620860)

0 引言

无线传感器网络具有体积小、重量轻、价格低廉等特点，被广泛应用于气象预报、目标跟踪、火灾监控等领域[1-2]。本文主要研究传感器网络对目标的跟踪问题，采用传感器调度技术根据某种准则确定传感器网络的最佳工作模式[3]，此类问题可以看作凸优化问题[4]，包含两方面内容：一方面是建立目标函数；另一方面是对目标函数求解得到调度方案。基于优化理论，常见的调度方法有：基于协方差矩阵的调度方法[5]、基于熵理论的调度方法[6]、基于后验克拉美罗下界的调度方法[7]、基于马尔科夫决策过程的调度方法[8]、基于智能算法的调度方法[9-10]以及其他自适应控制方法[11]。

以上方法仅从对目标的跟踪性能上考虑调度问题，以目标跟踪效果的好坏评价调度方案的优劣。与雷达等大型供电供能传感器不同之处在于，无线传感器网络供能来源于固定电池，而电池容量是有限的，因此，在调度过程中，也应同时考虑传感器网络的能量消耗问题，在提高跟踪效果和节省能量延长传感器网络使用寿命之间找到平衡[12-13]。

分布式网络结构不需要将数据传输到信息处理中心，每个传感器自身具有信息处理功能，从而大大减小了传感器之间的通信能量消耗[14-15]。因此，本文针对分布式无线传感器能量管理问题，提出基于能量限制的分布式无线传感器网络调度方法。

1 分布式目标状态估计方法

1.1 分布式无线传感器网络

在分布式无线传感器网络中，每个传感器除具有一般传感器具有的信息收集功能和信息传输、接收功能外，还同时具有信息处理和决策功能，即能将自身收集到的目标信息与接收到的来自其他传感器的目标信息进行融合，得到关于目标状态的更佳估计，同时能够进行自主决策，决定将自身收集到的信息是否传递给其他传感器、传递给哪个传感器。

为节省传感器计算能量消耗及传感器之间的盲目信息传输消耗，设置“头领传感器”。在观测时刻k，设对目标t观测的传感器集合为λk(t)，“头领传感器”记为hk(t)，hk(t)∈λk(t)；λk(t)内的其他传感器统称为“成员传感器”，位于传感器网络不能观测到该目标的传感器称为“闲置传感器”。在观测时刻k，传感器集合中的所有传感器将收集到的目标信息传递给该hk(t)，由hk(t)对目标信息进行融合得到关于状态信息的最佳估计并将估计结果发送给到k+1时刻的“头领传感器”hk+1(t)，并由hk+1(t)将目标信息发送给集合λk+1(t)中的其他传感器，以便传感器能够对准目标快速获取观测值。

按照上述传感器网络对目标的跟踪框架，目标跟踪过程如图1所示。

图1 传感器视域及目标跟踪示意图Fig.1 The FOV of sensors and the tracking process

在观测时刻k，设对传感器的调度方案为Ak，由Ak得到λk(t)。“成员传感器”仅需按照传感器调度指令对目标进行探测，获得观测值后将目标信息传递给“头领传感器”。而“头领传感器”需要进行如下活动：

1)对目标进行观测，获得观测值；

2)接收“成员传感器”发送的关于目标状态的信息，并通过滤波算法对观测信息进行融合；

3)计算k时刻和k+1时刻的观测时间Tk-k+1；

4)预测k+1时刻目标状态，以此为依据确定Ak+1、λk+1(t)和hk+1(t)，并将关于目标的状态信息传递给λk+1(t)中的传感器。

1.2 目标跟踪理论

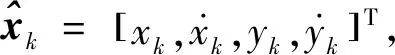
(1)

(2)

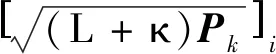
基于UKF目标状态估计过程为：

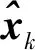
步骤3 传递目标状态样本和量测样本

(3)

步骤4 时间更新

(4)

(5)

步骤5 量测更新

(6)

(7)

步骤6k+1时刻，根据传感器si观测值，对目标后验状态估计均值和协方差矩阵为：

(8)

步骤7 融合估计。设k+1时刻共有nk+1个传感器对目标观测，则对目标状态估计得最终融合结果为：

(9)

2 基于能量限制无线传感器调度

2.1 传感器调度目标函数

在整个传感器网络对目标的跟踪过程中，消耗能量的过程主要有以下几个方面：

1)传感器对目标状态进行观测；

2)传感器之间数据传送；

3)传感器对信息进行处理。

根据以上分析，传感器在k时刻调度以获取k+1时刻的观测值的过程中应从以上三方面入手减小能量消耗，同时尽量增大较大的传感器对目标观测的时间间隔，故在调度中，目标函数为：

(10)

约束条件为：

(11)

由于在k时刻尚未获知k+1时刻关于目标的量测及估计状态，故在估计过程中均采用式(6)—(7)中的预测值代替。

一般情况下，若观测时间序列较长，常采用长时调度方法，不仅考虑某个时刻最优，而且进一步考虑整个时间段最优，通常选择一个时域周期TH，且TH通常取值范围为TH～{2,3,4,5}，在该时域周期内计算传感器调度方案，则该调度问题转化为“滚动时域调度”[16]问题，目标函数为：

(12)

约束条件为：

(13)

2.2 模型分析

(14)

式(14)中，nk+1为传感器个数，esen为单个传感器获取观测值消耗的能量。

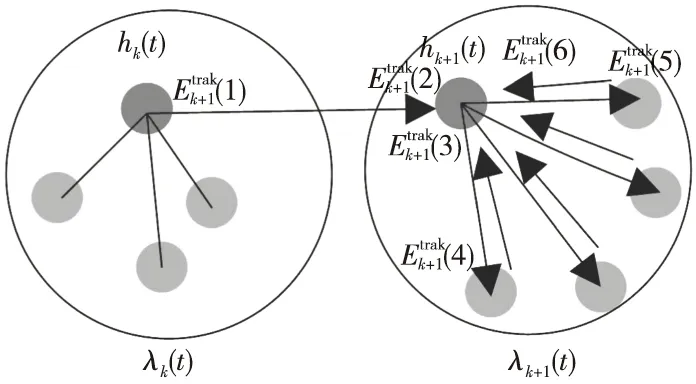
图2 信息传递能量消耗Fig.2 The energy consumption in information transmitting

(15)

传感器si发送Kbit信息到传感器sj消耗的能量为：

E(1)=eK+eampKdλ

(16)

式(16)中，e为发射每bit信息所需能量；eamp为放大器放大每bit所需能量；d为两个传感器之间的距离；λ为距离衰减系数，一般有λ≥2。

传感器sj接收Kbit信息消耗的能量为：

E(2)=erecK

(17)

式(17)中，erec为接收每bit所需能量。

由于传感器之间交流的信息均为目标信息，不妨假定该信息均包含Kbit，根据以上分析，有：

(18)

综上，目标函数转化为：

(19)

约束条件通式(11)。若采用滚动时域调度(长时调度)方法，则模型转换为：

(20)

约束条件同式(13)。

2.3 观测周期分析

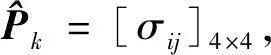
(21)

将上式对Tk-k+1求导，有：

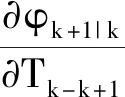
(22)

很明显，式(18)为关于Tk-k+1的单调增函数，当且仅当φk+1|k=φ0时，可取得最优值，故通过对如下公式求解，可得到最佳观测周期。

(23)

2.4 模型求解算法

在求得观测周期后，需要计算传感器调度方案，方案的求解过程是一个NP爆炸问题，且由于目标速度运动较快，要求算法具有计算时间短、求解精度高等特点。

由于布谷鸟捜索算法具有参数少、易扩展、全局搜索能力强、易于实现等优点[18]，本文引入布谷鸟算法求解传感器调度方案，并进行了一定的改进，用Boltzmann选择策略[19]代替基本算法中的Levy fights策略，在原有可行解的基础上生成新解，进一步提高算法搜索能力。

与Levy fights策略相比，Boltzmann选择策略具有稳定性、鲁棒性、并行性等优点，对初始解不敏感，具有较好的自适应性。在改进布谷鸟搜索算法中，基于Boltzmann选择策略的捜索步长公式为：

(24)

(25)

式(25)中，randn为生成随机数函数。

基于Boltzmann选择策略的改进布谷鸟算法流程如下：

2)算法运行开始。

when(K≤Number 1)

进行如下判断：

forj=1:Number 2

end

一部分适应度较差的鸟巢以概率Pa被抛弃并在相应位置生成新解；

适应度较优的鸟巢延续到下一次迭代；

记录种群中的最优鸟巢及适应度值；

K=K+1

end

3)输出最优解。

3 仿真分析

分布式传感器网络在1 000 m×1 000 m的分布位置及目标的运动轨迹如图3所示。传感器的探测半径和通信半径均为150 m，目标初始时刻位置为(510,190)。

图3 传感器分布及目标运动轨迹Fig.3 Distribution of sensor networks and the motion trajectory of the target

3.1 调度方案计算过程仿真分析

在初始时刻，采用本文提出的改进布谷鸟算法计算传感器调度方案，并与其他算法进行对比，传感器调度方案的生成过程如图4所示。其中，改进算法记为算法1，基本布谷鸟算法记为算法2，狼群算法[20]记为算法3，粒子群算法[21]记为算法4。

图4 优化算法对比Fig.4 Comparison of optimization algorithms

由图4可知，与其他三种算法相比，改进布谷鸟算法收敛速度明显提升，且具有较好的求解质量。

3.2 传感器短时调度分析

采用短时调度方法对传感器进行调度。在目标运动过程当中，当需要调度传感器对目标进行观测时，采用本文提出的改进布谷鸟算法生成传感器调度方案。对目标的轨迹估计图像及目标轨迹如图5所示。

图5 传感器调度方案及目标轨迹估计结果Fig.5 The sensor scheduling scheme and estimation of target’s motion states

如图5所示，“+”轨迹为目标实际飞行位置，“◇”轨迹为对目标状态的估计值；“头领传感器”为黑色实心“·”，“成员传感器”为灰色实心“·”，“闲置传感器”为黑色空心“·”。在25个时刻中，仅有14个时刻传感器对目标进行了观测，这14个时刻分别为：k=1，k=2，k=4，k=6，k=8，k=9，k=14，k=15，k=17，k=18，k=20，k=21，k=23，k=25。

图6 方法对比曲线Fig.6 Comparisons of scheduling methods

由图6可知，与其他两种方法相比，本文方法在保持较好的目标跟踪效果的同时，能够大大减小传感器网络能量消耗，从而有效提高传感器网络寿命。

3.3 传感器长时调度分析

采用长时(滚动时域)调度方法对传感器网络进行调度，从而对目标进行跟踪。目标运动过程当中，当需要调度传感器对目标进行观测时，采用本文提出的改进布谷鸟算法生成传感器调度方案。

分别取TH=2，TH=3，TH=4三种情况，传感器调度过程中，对目标跟踪的累积位置误差、累积能量消耗和平均计算时间如表1所示。在仿真过程中，由于TH=5时，计算量过大，在时间间隔内不能及时计算出传感器调度位置，故不再考虑。TH=1时即为短时调度。

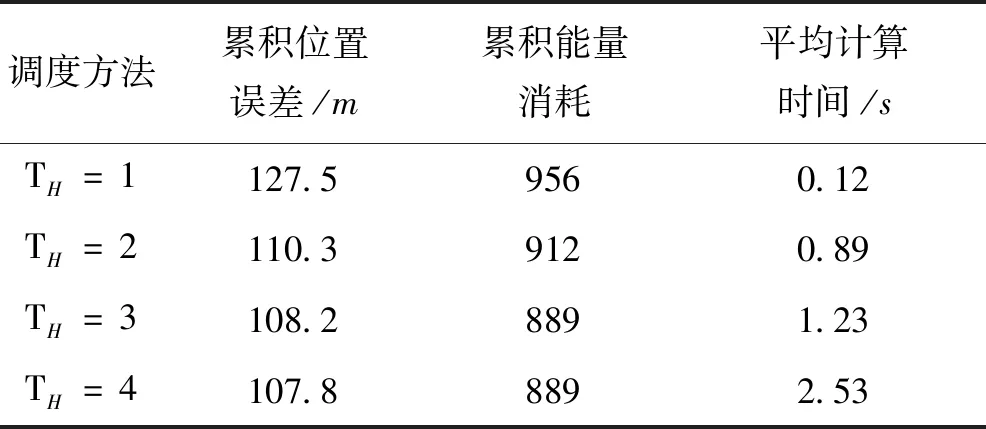
表1 调度方法对比结果Tab.1 The comparison result of sensor scheduling methods

由表1可知，与短时调度方法相比，长时调度方法虽然能够减小对目标状态的估计误差，降低传感器网络能耗，但是以提高计算时间为代价，且计算时间大幅增加。一般情况下，为缩短计算时间，为其他操作留出响应时间，采用短时调度即可满足相应需求。

4 结论

本文提出基于能量限制的分布式无线传感器网络调度方法。该方法同时考虑传感器感知能量消耗、传输能量消耗以及计算能力消耗建立传感器调度目标函数，并采用基于Boltzmann选择策略的改进布谷鸟算法求解传感器调度方案。仿真实验验证结果表明，为节省计算时间，在目标状态改变速度较快的情况下，选择本文提出的短时调度方法既能缩短调度方案的计算时间，又能获得较好的目标跟踪效果。