修正转移概率IMM-SRCKF固定单站无源跟踪算法

相飞华，王杰贵，唐希雯，孙 兵

(国防科技大学电子对抗学院，安徽 合肥 230037)

0 引言

无源定位跟踪系统具有隐蔽性强、探测距离远及适用范围广等优点，而单站无源定位跟踪系统更是具有极大的战术灵活性，因此成为目标跟踪领域的研究热点之一[1-2]。在机动目标的跟踪中，单一模型滤波器常无法与目标实际运动模型匹配导致滤波发散，难以达到跟踪目的。

交互多模型(interacting multiple model, IMM)算法较好地解决了模型匹配切换问题因而得到广泛的应用[3]。IMM算法使用多个子模型并行工作，各子模型通过Markov概率转移矩阵进行切换，将各模型滤波器输出的加权和作为目标运动状态的最终估计[4]。

IMM算法通过概率转移矩阵来实现模型切换，匹配目标真实运动状态，但目标发生机动会带来切换滞后的问题[5]。Markov矩阵的选取受到固定先验信息和人为因素影响，通常设为固定的主对角占优矩阵[6]。Markov矩阵先验信息的不确定会使滤波精度下降[7]，因此长期以来，转移概率的在线自适应估计成为研究的热点，文献[6,8—9]给出了几种不同的修正方法。考虑到当前量测中包含有系统当前的模式信息，因此应充分利用当前的量测信息，实时更新多模型滤波器的转移概率参数，以提高模型的切换速度和滤波精度。本文讨论了一种较为简便的方式，并给出了利用量测数据在线估计模型转移概率的递推公式。

滤波器的选择通常会直接影响IMM算法的滤波效果，机动目标跟踪系统通常需要选择合适的非线性滤波器。经典的扩展卡尔曼滤波(extended Kalman filter, EKF)存在明显的一阶线性化截断误差，且对于强非线性系统滤波易发散。粒子滤波(particle filter, PF)运算开销巨大，目标跟踪实时性差。无迹卡尔曼滤波(unscented Kalman filter, UKF)[10-11]估计精度可达二阶以上， IMM-UKF算法已经得到了广泛的应用[12]，但在处理高维系统(n>3)时需要精细的调节参数才能达到较高的精度。

容积卡尔曼滤波(cubature Kalman filter, CKF)[13-14]估计精度可达3阶，具有更好的非线性逼近能力，数值精度和稳定性更高。IMM-CKF跟踪效果好于IMM-UKF[15]，但需进行矩阵开方运算，误差协方差矩阵的非负定性和对称性易破坏，导致滤波发散，严重影跟踪性能。平方根容积卡尔曼滤波(square-root cubature Kalman filter, SRCKF)算法通过引入QR分解，避免矩阵开方运算，直接用协方差矩阵的平方根迭代计算，因此运算开销降低，计算效率提高；同时在更新过程始终保持协方差矩阵的对称性和非负定性，滤波精度和稳定性显著改善[14]。

本文针对传统IMM算法转移概率矩阵固定不变，模型转换慢滤波精度低的问题，提出一种修正转移概率IMM-SRCKF固定单站无源跟踪算法。该算法在引入时变转移概率方法的同时，将SRCKF与IMM算法结合，对机动目标跟踪实时性、滤波精度及稳定性有改善和提高。

1 固定单站无源定位模型

1.1 状态方程

二维平面内，固定单个观测站对空中机动辐射源目标进行无源定位，其系统模型如图1所示。设观测站在原点位置，k时刻辐射源目标位置为T(x,y),相对于观测站O的径向距离为rk，方位角为βk。

图1 固定单站无源定位二维平面图Fig.1 Two-dimensional plan of fixed single station passive location

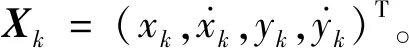
Xk+1=FXk+GWk

(1)

式(1)中，F(t)为状态转移矩阵，G(t)为状态噪声转移矩阵，Wk为状态噪声。

1.2 量测方程

在二维平面直角坐标系下，目标辐射源的空域和频域信息可由固定单站无源定位模型获得，本文以目标方位角、角速度和多普勒频率变化率为观测量。目标状态向量与观测向量的关系为：

Zk=h(Xk)+Vk

(2)

式(2)中，h(·)是状态向量到观测量的非线性变换函数，Vk表示量测噪声，是均值为零的高斯白噪声，其协方差矩阵为Rk。

(3)

显然，上述定位模型的状态方程为线性，量测方程为非线性，若要实现固定单站对运动辐射源的无源定位，应当采用非线性滤波算法进行递推估计。

2 修正转移概率IMM-SRCKF

2.1 IMM-SRCKF算法

SRCKF在CKF基础上，使用QR分解代替Cholesky分解，引入协方差矩阵的平方根，避免矩阵开方运算，提高了滤波的精度和稳定性。

对于式(1)、式(2)所表示的定位系统，首先根据状态向量维数计算容积点和权值。

(4)

式(4)中，[1]=[I,-I],I为单位阵，[1]i表示[1]的第i列，m=2n，i=1,2,…,n，式(1)所表示的状态方程中n=4。

SRCKF算法运行流程如下：

1)时间更新

①计算协方差矩阵Cholesky分解：

(5)

②计算容积及其经过状态方程传播的容积点(i=1,2,…,m)：

(6)

(7)

③计算状态向量的一步预测：

(8)

④计算预测协方差阵的平方根：

(9)

式(9)中，Tria(·)表示对矩阵进行QR分解运算。

(10)

(11)

2)量测更新

①计算容积点(i=1,2,…,m)：

(12)

②计算量测方程传播容积点：

(13)

③计算量测的一步预测值：

(14)

④计算新息协方差阵的平方根：

(15)

(16)

(17)

⑤计算互协方差阵：

(18)

(19)

⑥计算增益矩阵：

(20)

⑦计算状态向量更新：

(21)

⑧计算误差协方差阵平方根更新：

Sk+1|k+1=Tria([Xk+1|k-Kk+1Zk+1|k，Kk+1SR,k+1])

(22)

将IMM思想与SRCKF相结合形成IMM- SRCKF算法，该算法包括模式交互、模式条件、滤波模型概率更新、估计融合四个步骤。运算流程如下：

1) 模式交互

(23)

(24)

(25)

(26)

2) 模式条件滤波

3) 模型概率更新

假定模型i的新息服从高斯分布，则其似然函数和模型概率更新如下：

(27)

(28)

计算新息及其协方差矩阵：

(29)

4) 估计融合

(30)

(31)

2.2 模型转移概率实时修正

上节所述IMM-SRCKF算法假定输入交互为Markov过程，各模型之间的转换服从Markov链，即：

P{mk+1=m(j)|mk=m(i)}=πij,i,j=1,2,…,r

(32)

输入交互时各模型的权值大小由转移概率决定，在标准的IMM算法中，状态转移概率矩阵Pk是预先设定的，根据先验信息确定的，且在滤波更新过程中保持不变，而这种预先设定的矩阵并不是目标真实运动模式切换的概率。当目标辐射源存在强机动性或先验信息失真的情况，这种基于先验信息的状态转移矩阵无法真实反映目标运动模型之间的转换，就会造成跟踪滤波误差。因此考虑利用后验知识对矩阵Pk进行实时修正，由于当前的量测信息受到目标实际运动模型的影响，其中必然包含有后验信息。

(33)

由上式可以看出，当模型j的概率相比上一时刻增加时，κj(k+1)>1，当模型j的概率相比上一时刻减小时，κj(k+1)<1，因此，可以利用κj(k+1)与概率矩阵Pk相乘进行修正。假设k时刻矩阵Pk的第i行第j列的元素为πij(k)，可以用κj(k+1)对其进行修正：

πij(k+1)′=κj(k+1)πij(k),i,j=1,2,…,r

(34)

考虑到k+1时刻某一模型对于包括自身在内的所有模型转移概率之和为1，因此应对式(34)进行归一化处理。k+1时刻对于i,j=1,2,…,r，修正后的转移概率计算如下：

(35)

由式(35)可知，当模型j的概率随时间增大后，修正后的概率矩阵Pk第j列的元素也增大，则在下一时刻滤波过程前的模型交互时，模型概率大的模型(匹配模型)在交互过程所占的权值更大；相反，模型概率小的模型(非匹配模型)在交互过程所占的权值更小。通过量测数据自适应修正模型转移概率，强化了匹配模型的作用，而弱化了非匹配模型的作用。在滤波的模型转换过程中，赋予了匹配模型更大的权值，减小了非匹配模型的干扰，收敛速度和滤波精度得到提高。容易看出，修正之后的转移概率依旧满足转移概率的两条基本性质，即：

(36)

经过转移概率修正后的算法结构如图2所示(以三模型为例)。通过利用当前量测信息的在线修正模型转移概率的方法，增强了匹配运动模型的权重，降低了非匹配运动模型的权重，使得算法的稳定性提高，收敛速度及定位跟踪精度也得到改善。

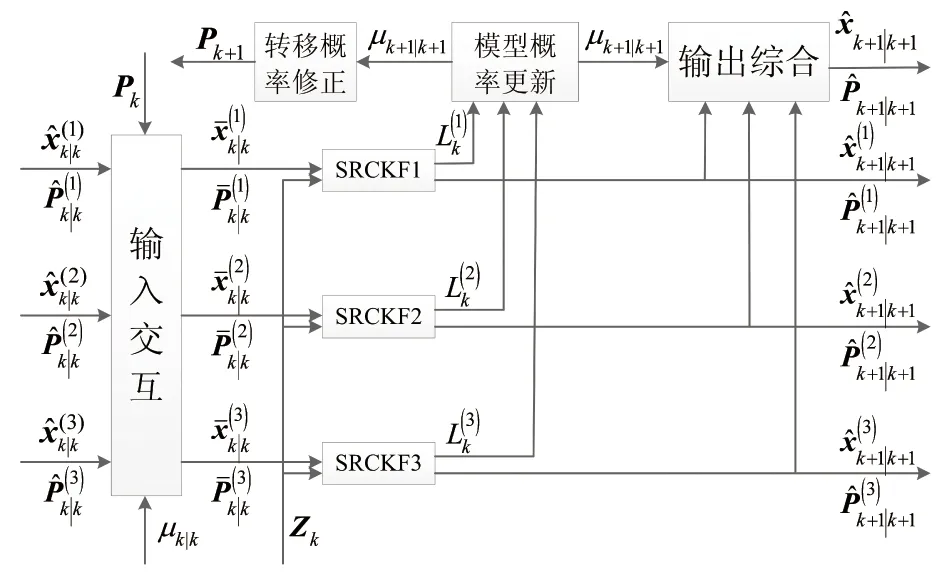
图2 修正转移概率IMM-SRCKF算法结构图Fig.2 Modified transition probability IMM-SRCKF algorithm structure

3 仿真与分析

为检验本文所提出算法的性能，并同时与IMM-CKF算法、IMM-SRCKF算法性能进行比较，设计如下的仿真实验场景。

在二维平面直角坐标系内，设固定观测站位于原点O，目标辐射源的初始位置和速度分别为(100,60) km和(-400,350) m/s，其实际运动过程如下：

1)t=0～20 s，匀速直线运动；

2)t=21～40 s，匀速转弯运动，角速度为ω1= π/18 rad/s；

3)t=41～60 s，匀速直线运动；

4)t=61～80 s，匀速转弯运动，角速度为ω2=-π/20 rad/s；

5)t=81～100 s，匀速直线运动。

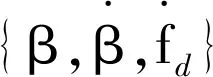
采用相对位置误差(relative range error, RRE)和相对速度误差(relative velocity error, RVE)描述算法的定位跟踪性能，定义式为：

(37)

(38)

进行Monte-Carlo实验100次，定位跟踪结束时刻RRE<5%和RVE<5%，则视本次实验收敛，否则视为发散。RRE和RVE的统计平均值和峰值为剔除滤波发散的结果。图3给出了三种算法的跟踪轨迹，图4、图5为三种算法的RRE和RVE结果，图6给出了三种算法跟踪过程中的模型转移概率，表1和表2分别为算法跟踪性能对比和算法稳定性及计算效率对比。

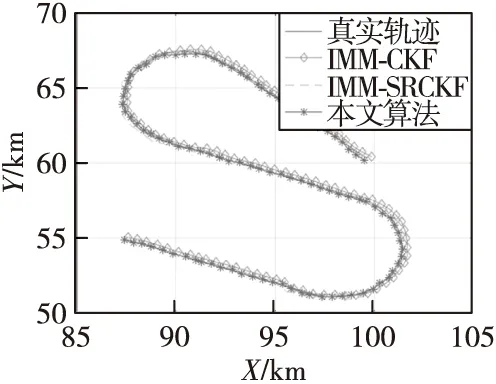
图3 跟踪轨迹对比Fig.3 Tracking trajectory comparison

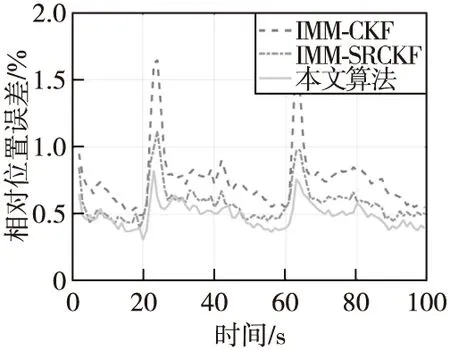
图4 相对位置误差对比Fig.4 Relative range error comparison

图5 相对速度误差对比Fig.5 Relative velocity error comparison

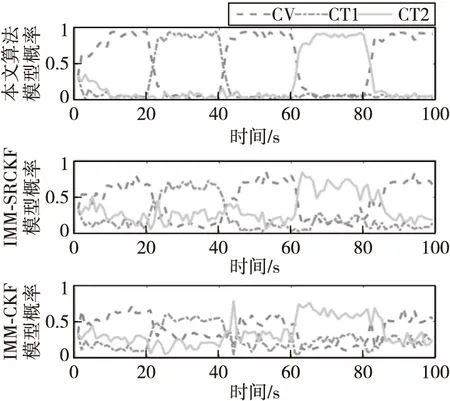
图6 模型转移概率对比Fig.6 Modified transition probability comparison

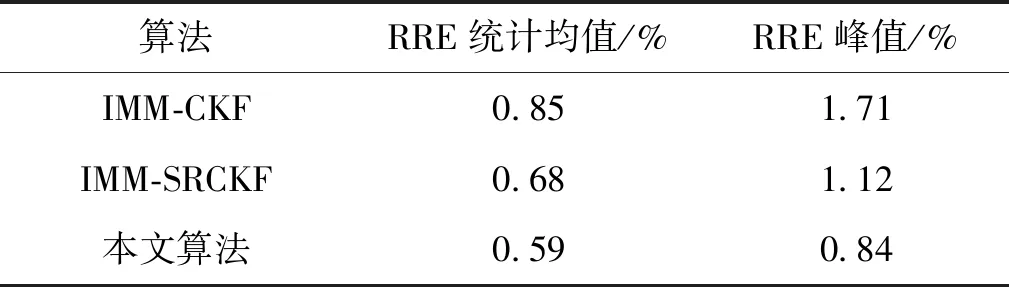
表1 跟踪性能对比Tab.1 Tracking performance comparison

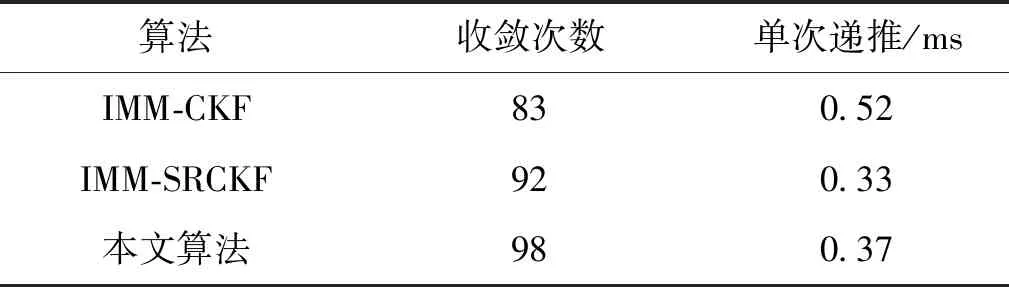
表2 算法稳定性与计算效率对比Tab.2 Comparison of algorithm stability and computational efficiency

由图表可以看出，在固定单站对机动目标无源跟踪过程中，本文提出的修正转移概率IMM-SRCKF算法相比IMM-SRCKF算法和IMM-CKF算法，具有更为优越的性能。具体表现在：

1) 跟踪滤波更精确。由图4、图5和表1可以看出，在对机动目标的位置估计和速度估计中，本文算法估计精度明显优于另两种算法，而同时IMM-SRCKF算法又优于IMM-CKF算法。尤其当目标机动状态发生较大变化时(如t=21 s和t=61 s)，三种算法跟踪精度均明显波动，本文算法依旧可以将误差波动控制在较小范围，其RRE统计均值和峰值均占优。

2) 模型匹配更合理。由图6可知，本文算法经修正转移概率后，模型切换更为迅速和合理，平均需要5～6 s时间，匹配模型的概率趋向于1，不匹配模型的概率则趋向于0。IMM-SRCKF和IMM-CKF算法模型切换则明显滞后，且主次模型的区分也不够理想。特别是IMM-CKF算法，转移概率分布比较混乱。对目标实际运动模型的良好匹配性能也是本文算法在跟踪滤波精度方面表现更好的主要原因。

3) 稳定性好，计算效率高。由表2可以看出，本文算法收敛次数最高，IMM-SRCKF算法次之，而IMM-CKF算法最低。计算效率方面，IMM-SRCKF算法效率最高，本文算法次之，而IMM-CKF算法最差。究其原因，本文算法与IMM-SRCKF算法均直接采用协方差矩阵平方根进行递推运算，避免了计算舍入误差的累积，保持了协方差矩阵的对称性和半正定性，其数值精度和稳定性更高，因此鲁棒性和实时性也更好。而本文算法因引入转移概率修改算法，增加了计算量，使其效率略低于IMM-SRCKF算法。在实际跟踪过程中，更为关注的是单次滤波的稳定性与实时性，综合考虑可以看出本文算法更为优秀。

4 结论

本文提出修正转移概率IMM-SRCKF算法，在传统IMM算法基础上引入在线修正转移概率方法，并将数值精度和稳定度更高的SRCKF作为模式滤波器。仿真实验结果表明，该算法在模型切速度、滤波精度和鲁棒性方面都好于传统算法，为解决固定单站对机动目标无源跟踪问题提供了一种可供参考的方法。