拖拉机—牵引式农机具的运动建模与跟踪控制*
张培培,杨自栋,赵相君
(浙江农林大学工程学院,杭州市,311300)
0 引言
拖拉机可以与附装的、悬挂的或牵引的农机具一起完成起垄、播种、喷药、收获等大部分田间作业。科技部在“数字农业”建设战略研讨会上提出,以“精准农业”和“智能农业”为切入点,组织实施数字化农业科技行动,实施精准农业,广泛应用智能农业机械,提高资源利用率和经济效益[1]。因此拖拉机自动驾驶技术已成为农业装备智能化研究热点之一[2-6],其研究方向主要分为车辆行驶轨迹规划和车辆轨迹跟踪控制两个方面。
随着控制技术的发展,国内外众多学者对拖拉机路径跟踪进行了建模并提出了相应的控制策略。应用较多的有PID控制[7]、模糊控制[8]、滑模控制[9]、模型预测控制(Model Predictive Control,MPC)[10]、非线性模型预测控制(Nonlinear Model Predictive Control,NMPC)[11]等。
拖拉机是与农机具或挂车完成田间作业,因此近十年来众多学者开始对拖拉机牵引农机具或者挂车系统进行自动驾驶的路径跟踪控制进行研究[11-15]。Backman等[11]建立了基于拖拉机—牵引式农机具运动学模型的NMPC路径跟踪系统,设计的NMPC控制器能够保证拖拉机和农机具在牵引速度12 km/h时的横向误差最大误差为10 cm。Kayacan等[12]建立了拖拉机挂车机组的纵向和横向的非线性动力学模型,设计的PID控制器使挂车机组有效地跟踪曲线路径。Cariou等[13]研究了农用车辆—牵引式农机具在地头转向和速度自动驾驶控制,并设计了基于运动学模型前进和倒退的路径跟踪控制器,系统以0.5 m/s速度倒车沿期望路径行驶80 m时,农机具的后轴中心的横向误差在±20 cm。Karkee等[14]研究了拖拉机单轴牵引农机具系统,分别建立了运动学模型、动力学模型和高度仿真模型,试验证明当牵引速度小于4.5 m/s和输入频率小于1 rad/s运动学模型能较好地反映车辆行驶时的运动学特性,并设计了基于拖拉机牵引农机具运动学模型的闭环LQR控制器跟踪期望路径。
本文针对拖拉机—牵引式农机具系统在运动轨迹假设的基础上建立运动学模型。该系统是本身存在一定运动约束的一类欠驱动系统,既独立控制输入少于自由度的系统,且具有非线性,因此为简化稳定跟踪控制器的验算和求解,本文应用准确线性化方法对建立的模型线性化,最后采用滑模变结构算法来实现对拖拉机—农机具系统的跟踪控制,并通过仿真手段分析和验证了控制算法的有效性和实时性。
1 运动学模型建立
为简化研究问题,作如下假设:车辆只作平行于地面的平面运动;车辆速度较低,车轮没有侧滑;拖拉机和牵引式农机具铰接点在拖拉机的后轴中心。这样,拖拉机—牵引式农机具系统就可以简化为如图1所示模型。
1.1 直线轨迹
拖拉机—牵引式农机具的直线行驶运动轨迹跟踪模型如图1所示,(XOY)为卡迪尔坐标系,使农机具跟踪X轴,X轴为期望路径,即控制目标为y2→0,θ→0,γ→0。
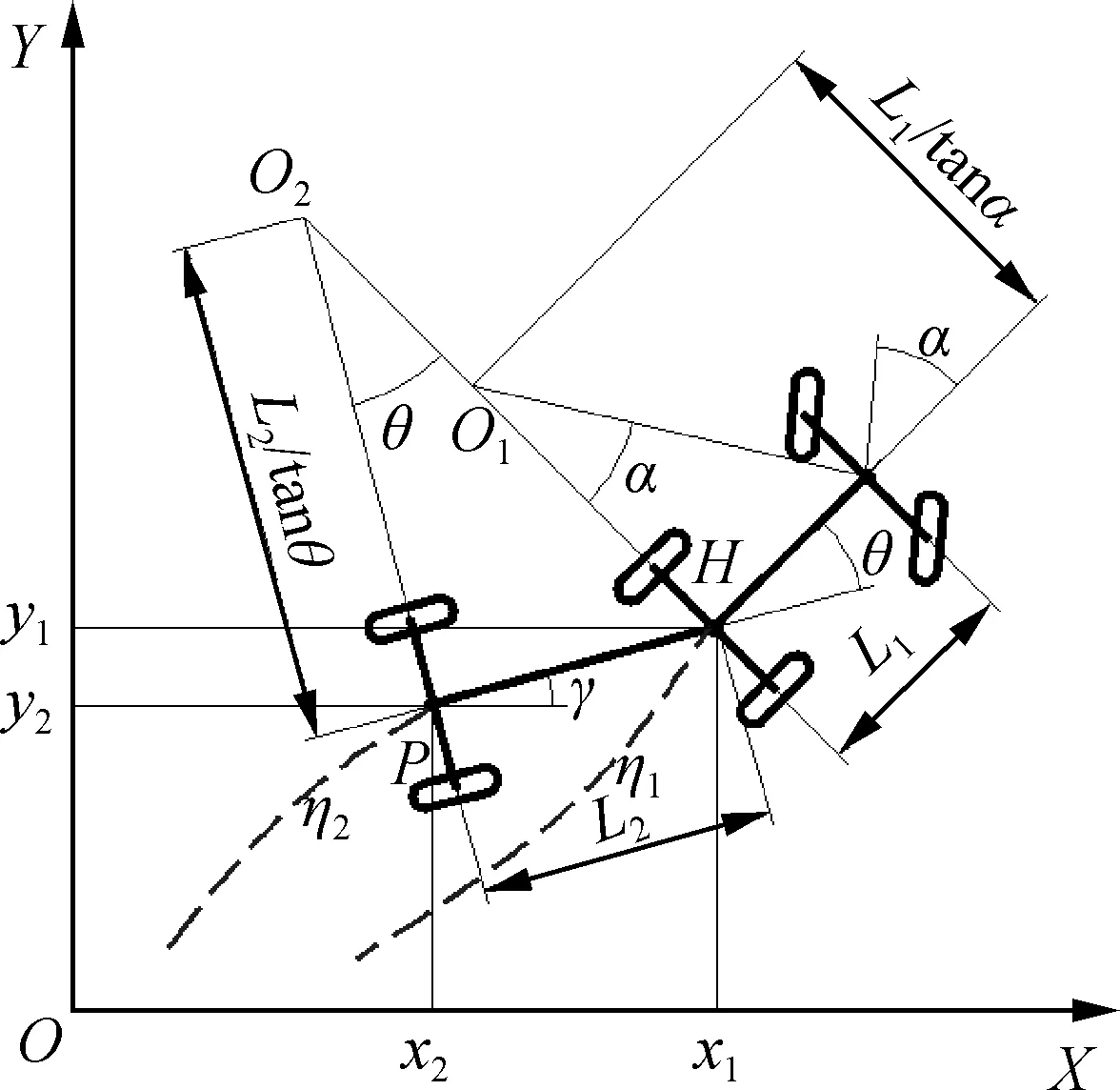
图1 拖拉机—农机具直线跟踪运动模型Fig. 1 Line path tracking model of tractor-trailer system
根据图1模型建立拖拉机—农机具系统的直线运动学微分方程
(1)
(2)
(3)
(4)

(5)
以P点横坐标x2为新的时间量标,新量标x2与时间t之间的关系
(6)
式中:V1——拖拉机后轴中心速度。
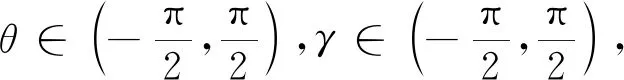
式(1)~式(5)可以改写为
(7)

(8)
(9)
则拖拉机—农机具的线性化状态方程
(10)
因此可以为该线性系统设计一个负反馈线性控制器u作为新系统输入
(11)
根据式(11),拖拉机前轮转角α如式(12)。
(12)
式(10)、式(11)表明,设计合理的负反馈控制器u会使系统快速稳定,当x2不断增大时,ξ→0,根据式(8)得到y2→0,θ→0,γ→0即车辆直线运动时会跟踪X轴。式(12)表明,前轮转角α由u、θ,γ决定。
1.2 圆弧轨迹
图2为拖拉机—农机具系统圆弧轨迹示意图,农机具车轴中心的期望路径的半径为R,农机具车轴中心的实际位置用极坐标(r,φ)表示,用以跟踪期望路径,极坐标的圆心为期望路径的圆心O,O1为拖拉机的瞬时回转中心,O2为农机具的瞬时回转中心。
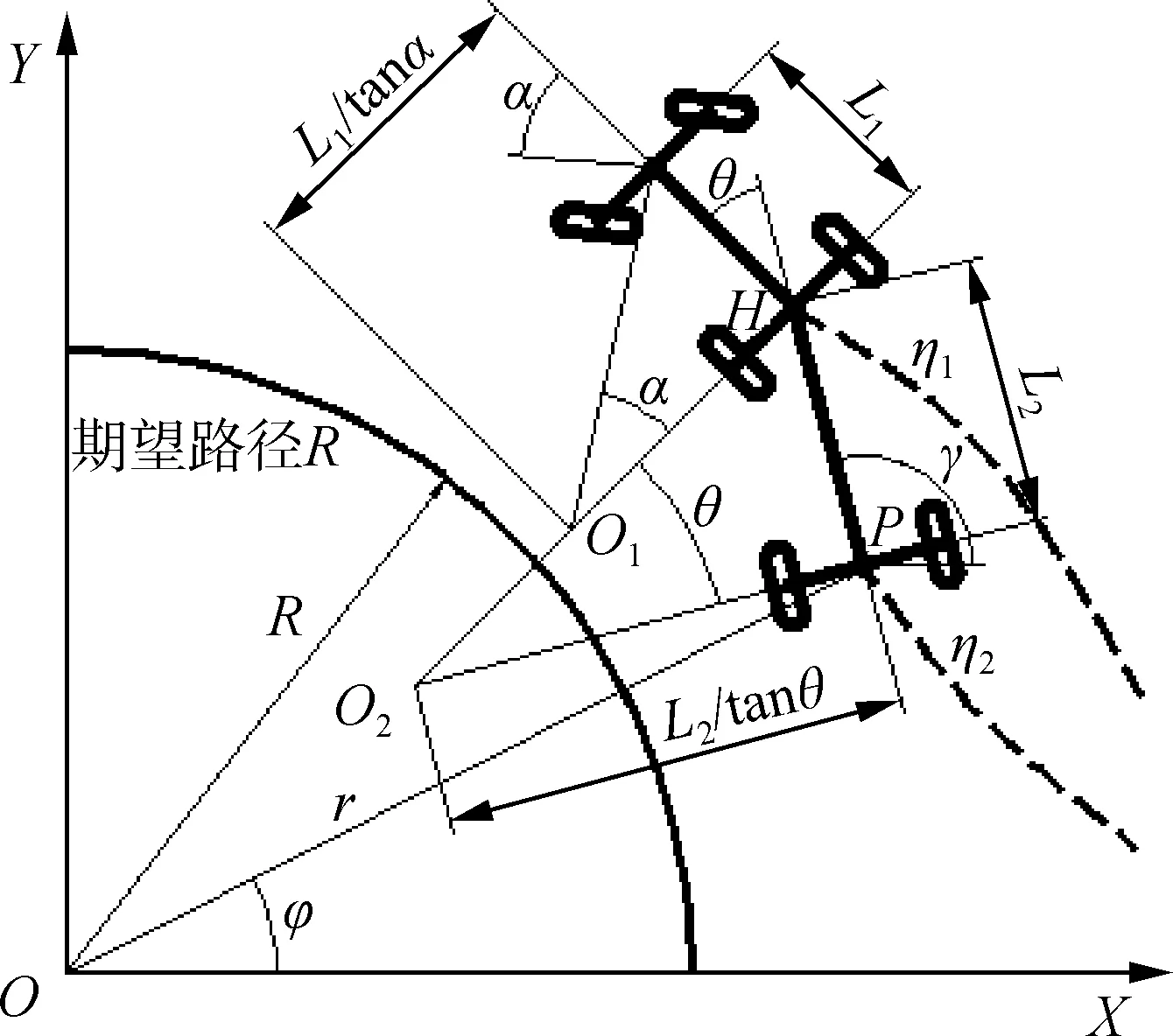
图2 拖拉机—农机具圆弧跟踪运动模型Fig. 2 Circle path tracking model of tractor-trailer system
以期望路径的弧长l=Rφ作为新的时间量标,以(r-R)→0,θ→定值,(γ-φ)→90°为控制目标。根据图2模型建立新量标l与时间t的关系和拖拉机—农机具的圆弧运动学微分方程
(13)
(14)
将式(14)通过坐标变换进行准确的线性化,得到与式(10)类似的系统线性化模型。

(15)
(16)
根据式(16)可以求出拖拉机前轮转角α如式(17)。
(17)
设计合理的负反馈控制器u会使系统快速稳定,当新的时间量标l不断增加,ξ→0,r快速收敛到R。式(17)表明,极坐标系下拖拉机—农机具系统圆弧轨迹跟踪时拖拉机前轮转角α由u、r、θ和γ-φ决定。
2 基于滑模变结构控制算法设计
拖拉机—牵引式农机具系统具有明显的非线性,前面将该系统进行准确的线性化为反馈线性控制提供了基础。本文采用滑模变结构算法来实现对该线性化模型的跟踪控制。
2.1 滑模面的参数设计
设有线性系统
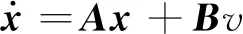
(18)
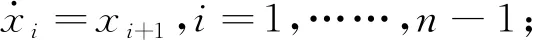
A、B——系数矩阵;
v——输出矩阵控制函数。
滑模面设计为
(19)

n——状态变量的维数。
根据本文建立的拖拉机—农机具的模型是一个三阶系统,即n=3。
2.2 基于指数趋近律和准滑动模态的滑模控制器设计
滑模控制包含趋近运动和滑模运动两个过程。为了保证快速趋近同时削弱抖振,本文采用指数趋近律的方法和准滑动模态控制。
指数趋近律
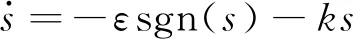
(20)
式中:ε——等速趋近速率,ε>0;
k——指数趋近项系数,k>0。
ε和k决定了趋近切换面时的速度。
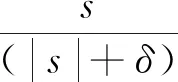
(21)
式中:δ——很小的正常数。
(22)
根据Lyapunov稳定性理论,系统是稳定的,结合式(18)~式(21)得到系统的变结构滑模控制律
(23)
合理地选择切换函数矩阵C可以保证滑模变结构控制系统具有良好的动态特性,C的选取方法主要有极点配置法、二次型最优等,Ackermann公式可以简单有效地进行极点配置[18],故本文基于Ackermann公式进行极点配置选取C。线性系统(18)是一个闭环三阶系统,具有3个都位于左半开复平面的极点,其中2个共轭主导极点λ1、λ2由系统的参数决定,为使第3个实数极点λ3对系统的影响小,应使其远离两个主极点。
根据文献[12]确定系统的固有频率和阻尼为ωn= 2.26 Hz,ζ=0.70,则主导极点
(24)
第3个极点λ3远离2个主导极点,取λ3=-10。
根据Ackermann公式
(25)
其中:f(A)=(A-Iλ1)(A-Iλ2)(A-Iλ3)。
根据式(25)可以求出c1=40.3,c2=32.0,c3=12.8,取ε=0.5,k=3,δ=0.01,则系统的滑模控制律为
(26)
3 路径跟踪仿真试验分析
一辆自制的青山牌轮毂电动拖拉机和小型半挂车组作为仿真试验用车,拖拉机的轴距L1=1.4 m,铰接点到半挂车轴的距离L2=1.2 m。
根据上述滑模变结构控制器的设计,搭建仿真模块并在Matlab/Simulink环境下分别进行拖拉机—农机具系统的直线和圆弧路径跟踪仿真,假设运动速度稳定在1 m/s。设置初始时刻为t0=0,末端时刻t1=30 s,求解算法采用龙格—库塔数值解法,设定模型仿真步长为0.01 s。
3.1 直线轨迹跟踪
系统的直线轨迹跟踪初始条件如下:y2=0.5 m,θ=0,γ=π/6,仿真试验结果如图3所示。
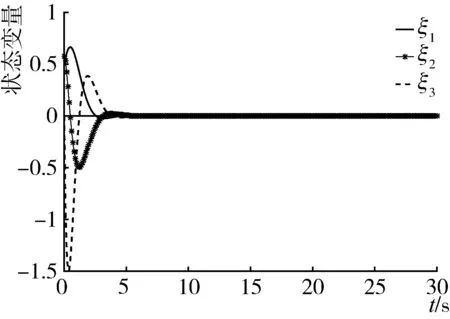
(a) 状态变量随时间变化历程
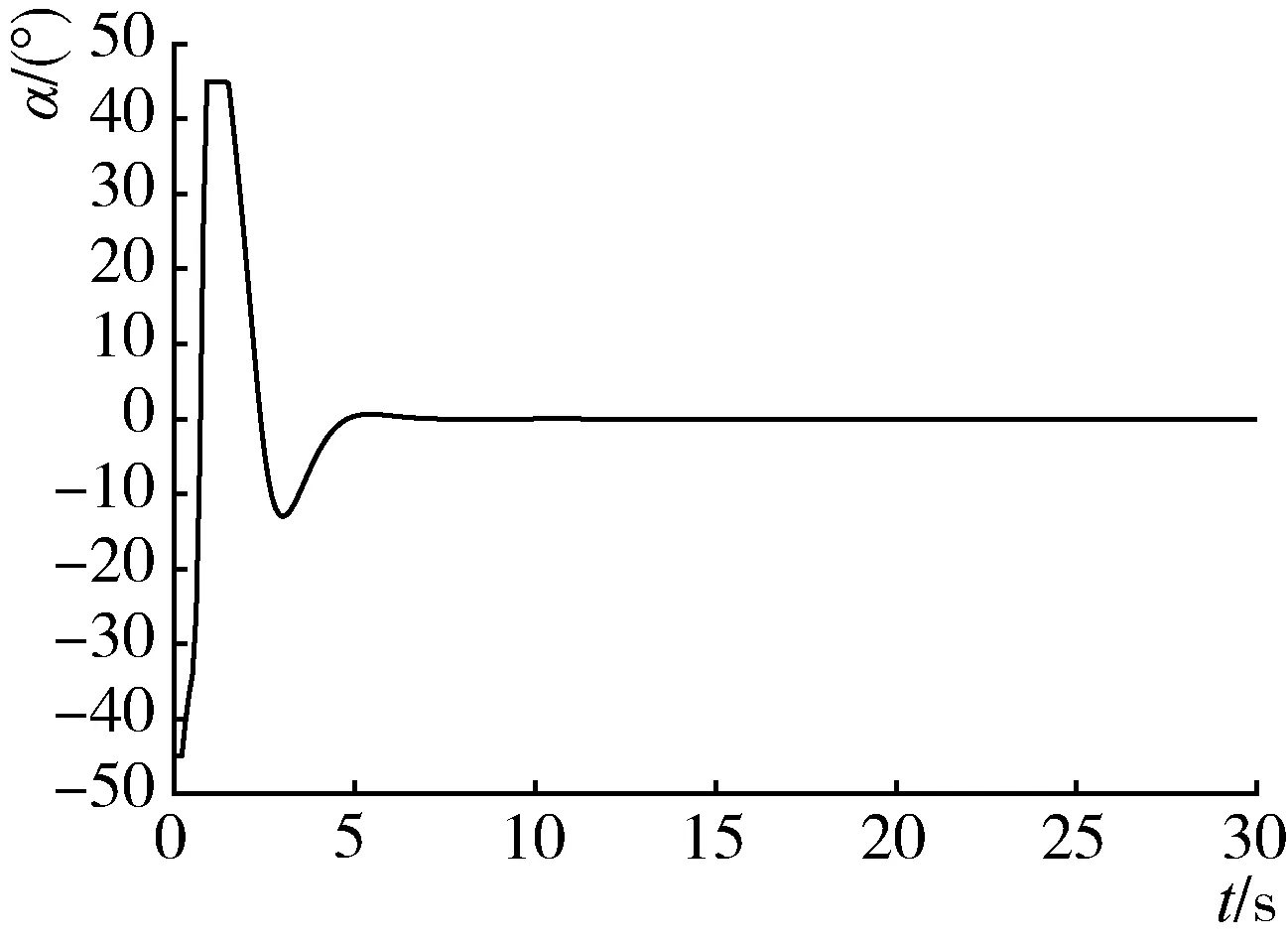
(b) 前轮转角随时间变化历程

(c) 农机具与拖拉机夹角随时间变化历程
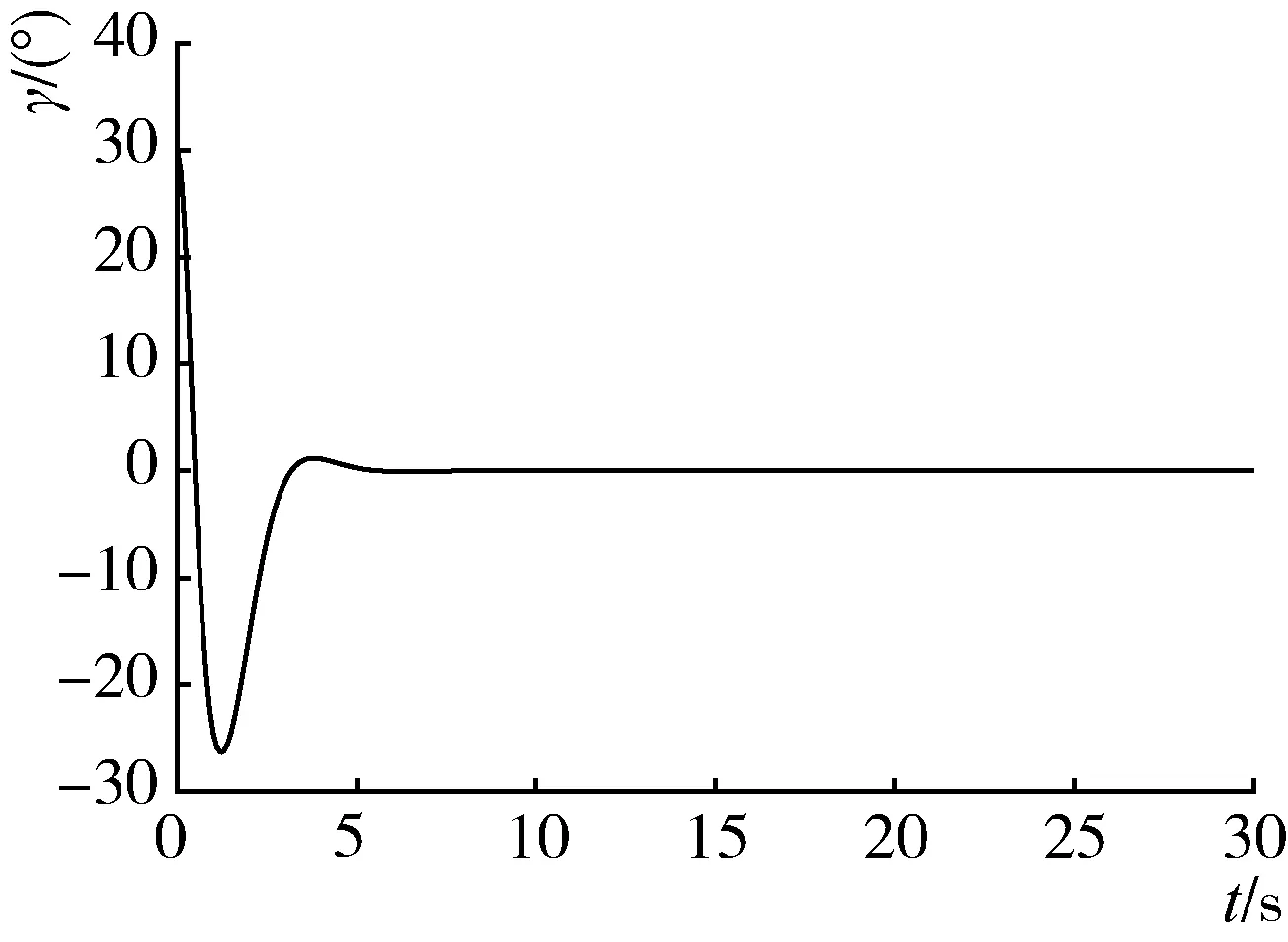
(d) 农机具与X轴夹角随时间变化历程图3 直线跟踪仿真结果Fig. 3 Straight-path-tracking simulation results
线性化系统的状态变量ξ经过约3 s 后均收敛到0,农机具的后轴中心P点的Y坐标y2=ξ1从初始位置0.5 m增大到约0.67 m后迅速收敛于期望路径X轴;前轮转角α经过约5 s收敛到0°;农机具与拖拉机夹角θ在(-60.26°,22.24°)波动后快速收敛到0°;农机具与X轴夹角γ在(-26.38°,30.00°)波动后约5 s后收敛到0°,说明农机具可以跟随拖拉机沿着期望路径行驶,因此设计的控制器可对直线轨迹进行跟踪。
3.2 圆弧轨迹跟踪
拖拉机—农机具系统的圆弧轨迹跟踪初始条件如下:r-R=1 m,θ=π/18,γ=π/2,φ=π/10。参考轨迹圆的半径依次设计为5 m、10 m和20 m,仿真试验结果如图4所示。

(a) 状态变量随时间变化历程
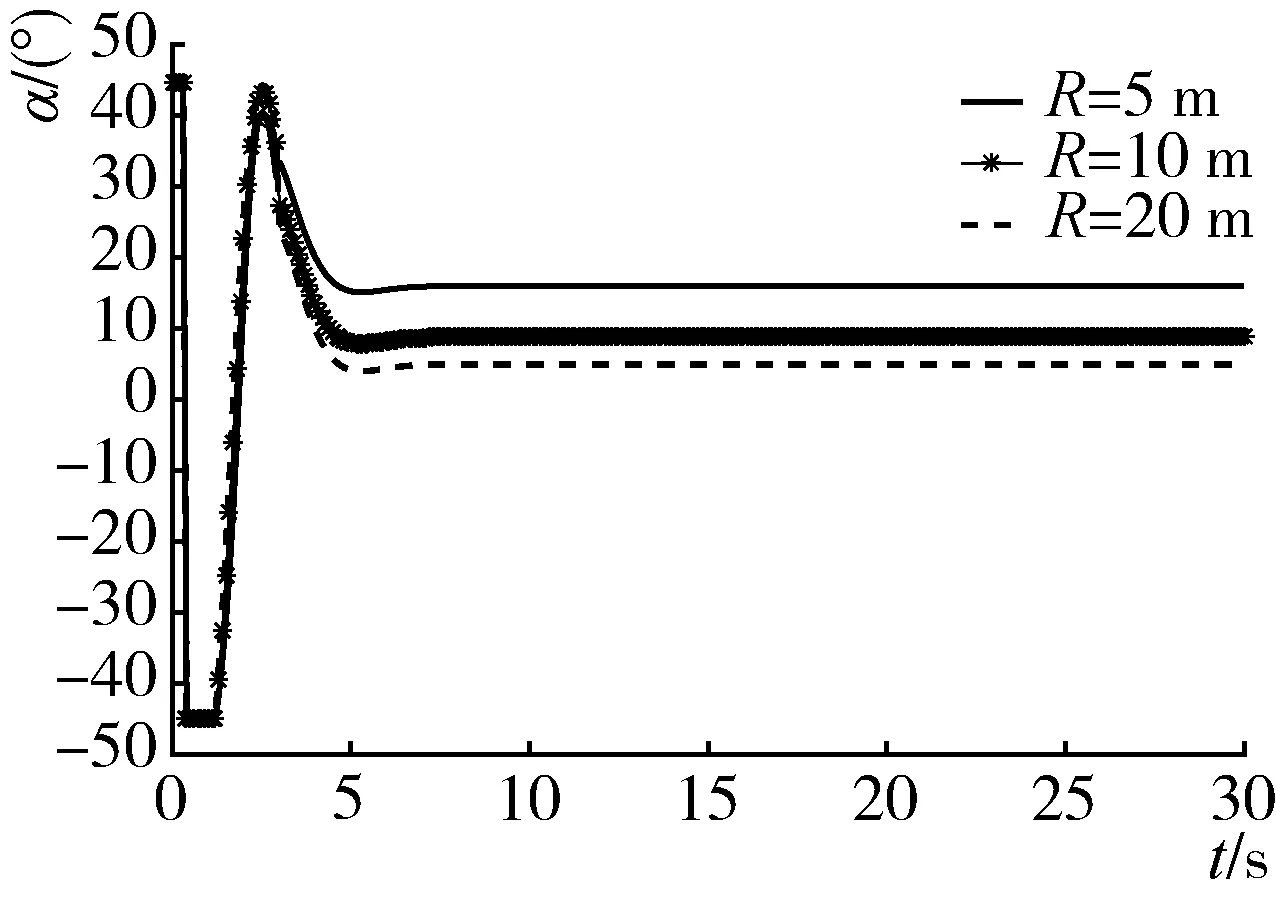
(b) 前轮转角随时间变化历程
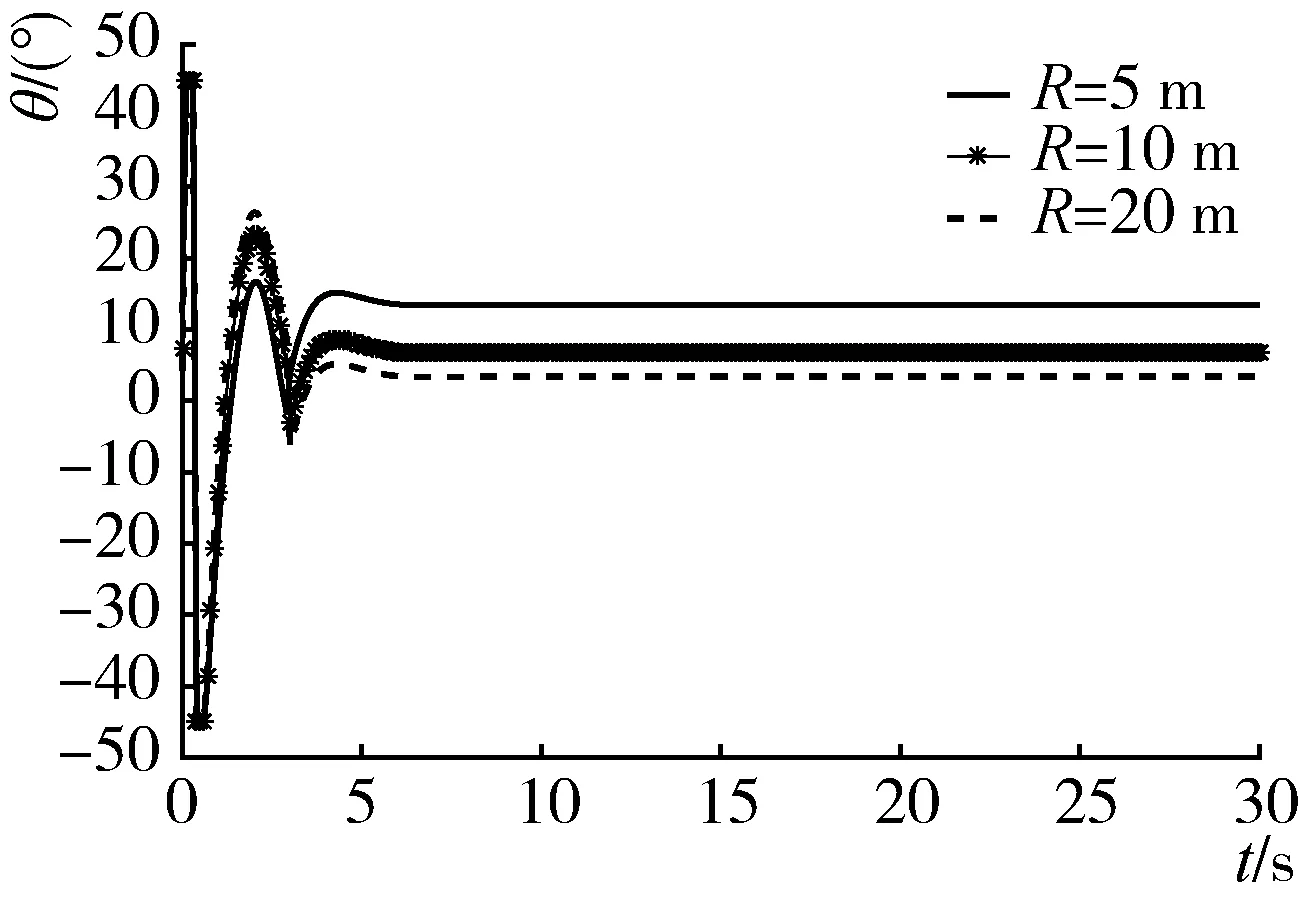
(c) 农机具与拖拉机的夹角随时间变化历程
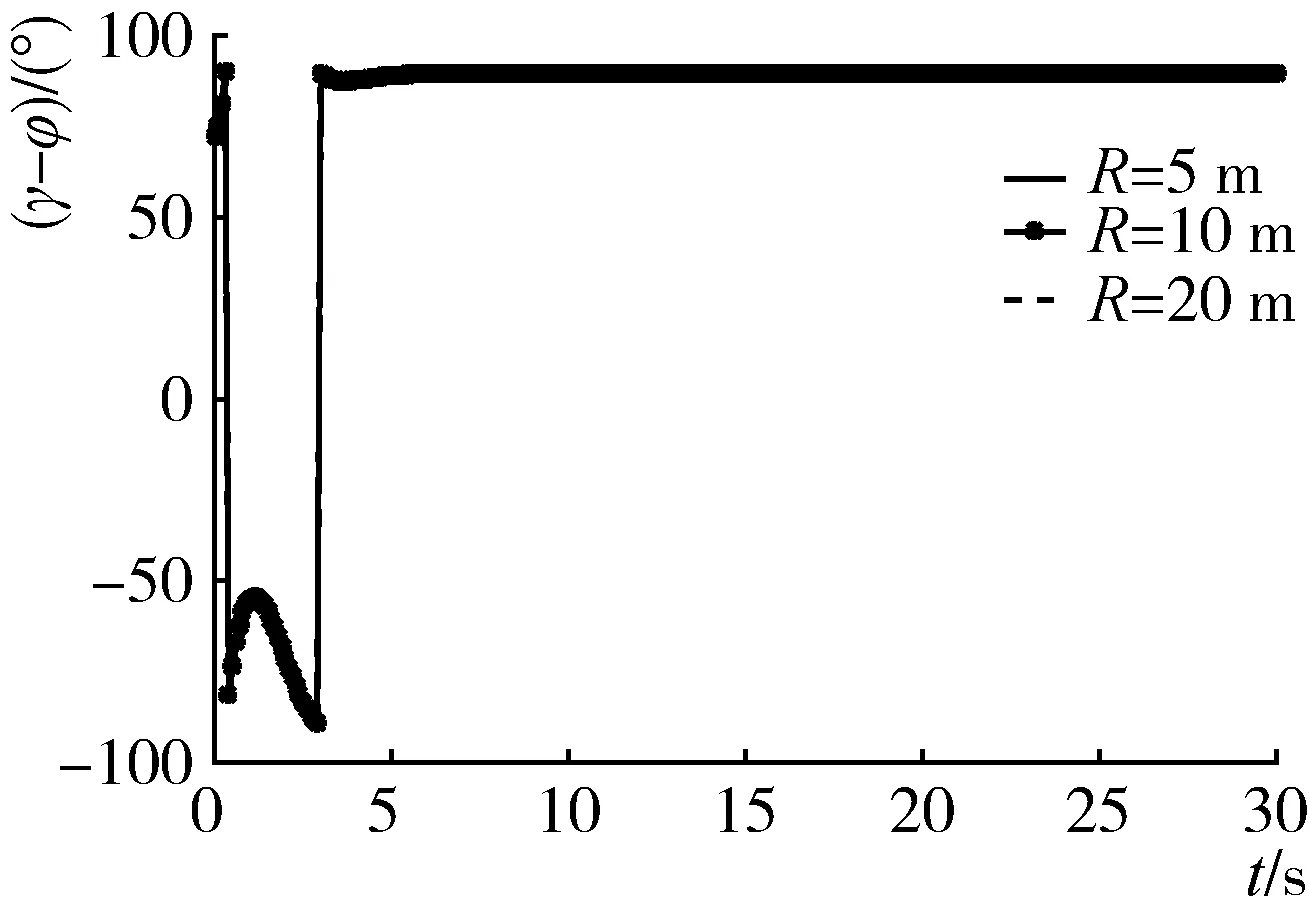
(d) (γ-φ)随时间变化历程图4 圆弧轨迹跟踪仿真结果Fig. 4 Curved-path-following simulation results
从图4(a)中看出,线性化系统的状态变量ξ经过约3 s收敛到0,农机具的车轴中心P点的实际半径与期望半径差(r-R)=ξ1从初始值1 m快速收敛到0。图4(b)、图4(c)和图4(d)可以看出,R依次为5 m、10 m 和20 m 时,前轮转角α经过约7 s分别快速收敛到期望值16.14°、8.97°和5.09°;农机具与拖拉机的夹角θ分别收敛到13.47°、6.81°和3.40°;(γ-φ)均快速收敛于90°,说明农机具的纵向中心轴线与期望轨迹圆弧快速相切,这些表明农机具的回转中心O2收敛于期望路径的圆心O,由此可见设计的控制器可对曲线轨迹进行跟踪。
4 结论
1) 应用非线性相关理论对欠驱动拖拉机—牵引式农机具系统动态规律进行了分析,以此建立了拖拉机—牵引式农机具系统的直线和圆弧行驶运动轨迹跟踪模型,为达到简化运动的目的,应用准确线性化方法对建立的非线性系统模型线性化。
2) 采用滑模变结构算法设计了拖拉机—牵引式农机具系统的跟踪控制算法。最后利用Matlab/Simulink对系统仿真试验,结果表明:设计的控制器可以使线性化系统的状态变量ξ经过约3 s收敛到0,在直线跟踪时,农机具从初始位置y2=0.5 m经过约3 s跟踪到期望路径X轴,农机具与拖拉机夹角及农机具角度偏移量均在5 s左右收敛到0°;在跟踪半径为5 m、10 m 和20 m的圆弧轨迹时,农机具车轴中心从偏离期望圆弧半径1 m的初始位置经过约3 s可以跟踪到期望圆弧,农机具与拖拉机夹角均可快速收敛到定值,同时农机具的回转中心O2收敛于期望路径的圆心O,因此农机具的后轴中心P点能迅速跟踪不同期望路径,验证了控制算法具有良好的道路跟踪精度和动态性。

