原棉压缩参数与力学指标的关系*
李勇,李健,雷福祥,张洪洲,闫树军
(1. 塔里木大学机械电气化工程学院,新疆阿拉尔,843300; 2. 西安交通工程学院,西安市,710300)
通讯作者:闫树军,男,1980年生,陕西蒲城人,硕士,讲师;研究方向为机械装置设计与应用。E-mail: yanshujun0218@163.com
0 引言
原棉是重要的纺织原材料,纤维材料以集合体形式存在于生产、生活各环节中,其形态蓬松,给其储运、流通带来不便。纤维材料紧密化加工是其高效生产加工的必然手段,其中机械压缩是常用的方法之一。秸秆、泡沫材料、原棉均属于散体材料,原棉的压缩分析方法与秸秆、泡沫的分析方法相一致。
目前,诸多研究者用经典理论、流变模型研究散体材料的压缩行为,其中黏弹塑性模型、压力与密度模型是分析散体材料压缩力学行为的典型模型。Dunlop[1]构建了原棉体积变化(库仑模型)模型,其可解释压缩过程中纤维滑移、变形滞后和不可回复等现象。Kaliyan等[2]构建了秸秆的线性黏弹塑性模型,得出弹性模量与黏性系数对材料的抗压强度有影响。霍丽丽等[3]研究了秸秆压缩成型,采用黏弹性理论建立了相应压缩本构模型,拟合效果较佳。马方等[4]基于Boltzmann 叠加原理建立了生物质压缩的非线性黏弹塑性本构模型,并发现生物质的纤维素、半纤维素、木质素等含量与材料的黏度相关。Cheng等[5]用等效围压来量化谷物仓中的压缩作用,建立力学模型预测压力与压缩密度的关系。Yan等[6]研究了木原棉的压缩行为,利用Nishihara模型模拟木原棉压缩的黏弹塑性形变。并表明试验参数与弹性模量和黏度密切相关,弹性模量和黏度可表征原棉压缩行为。
在黏弹塑性方面,原棉压缩力学规律尚未系统研究。本研究以原棉为研究对象,依据原棉压缩特性建立原棉的黏弹塑性本构模型,获得其压缩力学本构方程。结合主压缩参数,测试不同参数下原棉的应力变化曲线,分析压缩参数与其力学指标之间关系,为原棉的生产加工环节提供一定理论指导。
1 试验设计
1.1 试验材料
试验材料选用新疆阿拉尔市新陆中37手摘原棉。
1.2 试验仪器
万能材料试验机,YG715D恒温恒湿箱,Y802G八篮恒温烘箱,FA1104电子天平,FSR400薄膜压力传感器,有线薄膜压力传感软件,DSCa-01型数字式小样梳棉机,圆盘取样器。
1.3 试验方法
为使棉纤维取向一致,原棉经小样梳棉机梳理成棉网层(10层棉网叠加),利用圆盘取样器切出90 mm 棉网样片(厚度约3~5 mm,质量约4~6 g)。
称取160 g原棉(棉网样片),逐层依次装入亚克力圆筒(外径110 mm,壁厚3 mm,填充高度300 mm)中。利用万能试验机进行压缩试验(室内温度16 ℃~22 ℃,相对湿度38%~44%,压缩量250 mm),加载压头的下降(压缩)速度与上升(回复)速度设定为相同数值,薄膜压力传感器采集原棉压缩—回复的力值。
1) 循环加载试验。以100 mm/min的加载速度,循环加载(压缩、回复连续加载)原棉(回潮率4.2%)20次,传感器采集原棉压力—变形数据。
2) 不同加载速度压缩试验。以5、50、100、150、200、250、300、400 mm/min的加载速度,分别压缩原棉(回潮率4.2%)5次,传感器采集原棉压力—变形数据。
3) 不同回潮率压缩试验。利用恒温恒湿箱调节原棉的回潮率,每隔8 h抽取一定原棉计量回潮率(回潮率调节范围为4%~15%),将不同回潮率原棉划分10组,每组分别压缩5次(加载速度100 mm/min),薄膜压力传感器采集原棉压力—变形数据。
2 压缩曲线分析
棉纤维是原棉的基本组织单元,各纤维自身的排布形态杂乱,纤维间以网状结构堆砌成集合体态,原棉由棉纤维以及棉纤维间空隙组成,棉纤维间纠缠堆砌成集合体态。棉纤维的堆砌密度、排列形式及相互间作用决定了原棉的压缩力学性能[7-8]。
图1显示原棉(回潮率4.2%)的压缩回复曲线(加载速度100 mm/min)呈单调下凹状,压缩曲线和回复曲线不重合,存在显著的滞后性。此表明压缩环节原棉存在黏弹塑性,这是典型的高聚物受力变形曲线[9]。在压缩致密阶段,原棉的物理变化极为复杂,且其变形具有时间依赖性。
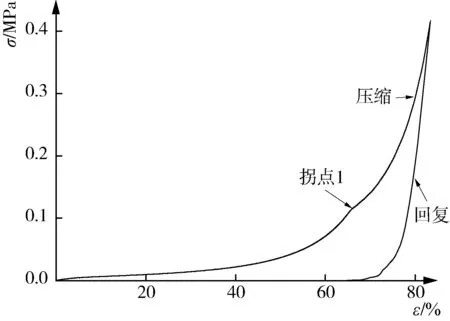
图1 原棉压缩回复曲线Fig. 1 Curve of compression and reversion of cotton
在压缩初期,原棉体积密度低,纤维间接触少,以纤维网屈曲为主。在压力推动下,棉纤维滑移,大量空气由纤维间排出,产生不可回复变形。少量空气与纤维形成具有黏性的混合流[10],形成黏弹性聚集体。棉纤维固有的黏阻性和受压后表现出的黏结性,使其致密成型过程中展现出黏弹性变形和黏塑性变形。随着压缩持续,原棉内部纤维变形趋于紧致、固化[11]。据此,将原棉的压缩过程分为3个阶段,即为非线性黏弹性(Ⅰ阶段,力值变化缓慢)、非线性黏弹塑性(Ⅱ阶段,力值增加较快)和高级黏弹性变形阶段(Ⅲ阶段,力值急剧增加)[12]。原棉黏弹性变形阶段和黏弹塑性变形阶段无显著分界点(其往往是弹性、塑性不断发展的过程,ε值取25.4%,此点定义为分界点),黏弹塑性阶段与高级黏弹性段存在显著的拐点1(拐点1处,ε值为65.9%,压力σ为0.115 4 MPa),其可定义为原棉的固化转变点。
在回复阶段,原棉由高压状态回复,其变形以弹性回复为主,兼有少量黏弹回复。
3 黏弹塑性模型
假设逐层堆叠的原棉是由材质均质、各向同性的棉纤维堆砌,近似地用力学模型表征其各阶段力学特性[13]。
1) 第Ⅰ阶段。原棉压缩过程中存在非线性黏弹性变形,用线性Hooke元件弹簧和Newton元件来表征非线性弹性应变和线性黏弹性应变组合[14],如图2所示。
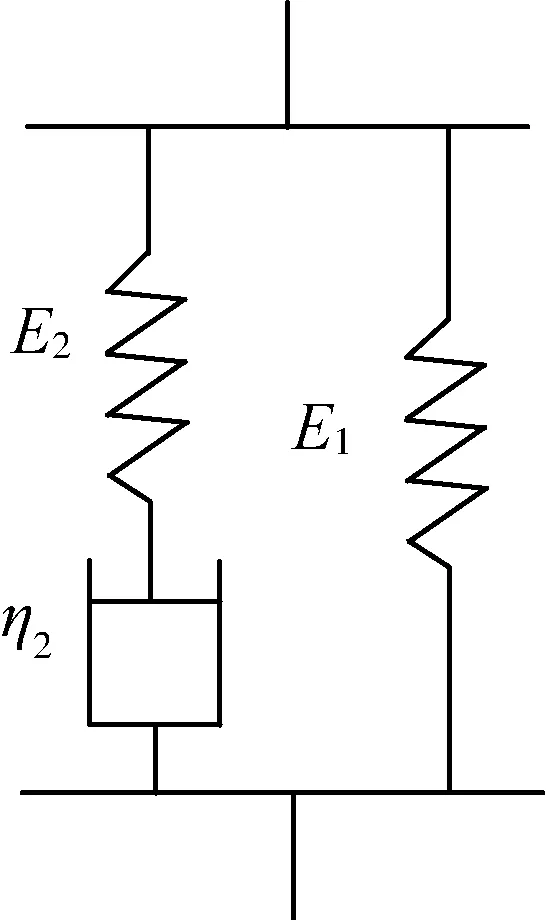
图2 非线性黏弹性模型Fig. 2 Nonlinear viscous-elastic model
非线性黏弹性变形的总应变为弹性应变与黏弹性应变之和,即
(1)
式中:E1——弹性元件的弹性模量,MPa;
E2——黏性元件的弹性模量,MPa;
η2——黏性元件的黏性系数,MPa·s。
经拉普拉斯变换和逆拉普拉斯变换,第Ⅰ阶段应力σ1与时间t的函数关系见式(2)。
(2)
式中:Kε——恒定的压缩速率,取100 mm/min。
2) 第Ⅱ阶段。原棉压缩过程中存在非线性黏弹塑性变形,用线性Hooke元件弹簧、Newton元件和线性Sl.Vennant元件摩擦块V来表征非线性弹性应变、线性黏弹性应变和非线性塑性变形组合,如图3。
该阶段黏弹塑性模型的力学本构关系见式(3)。
(3)
式中:σc——摩擦块V的屈服极限,MPa;
η1——黏塑性元件的黏性系数,MPa·s。
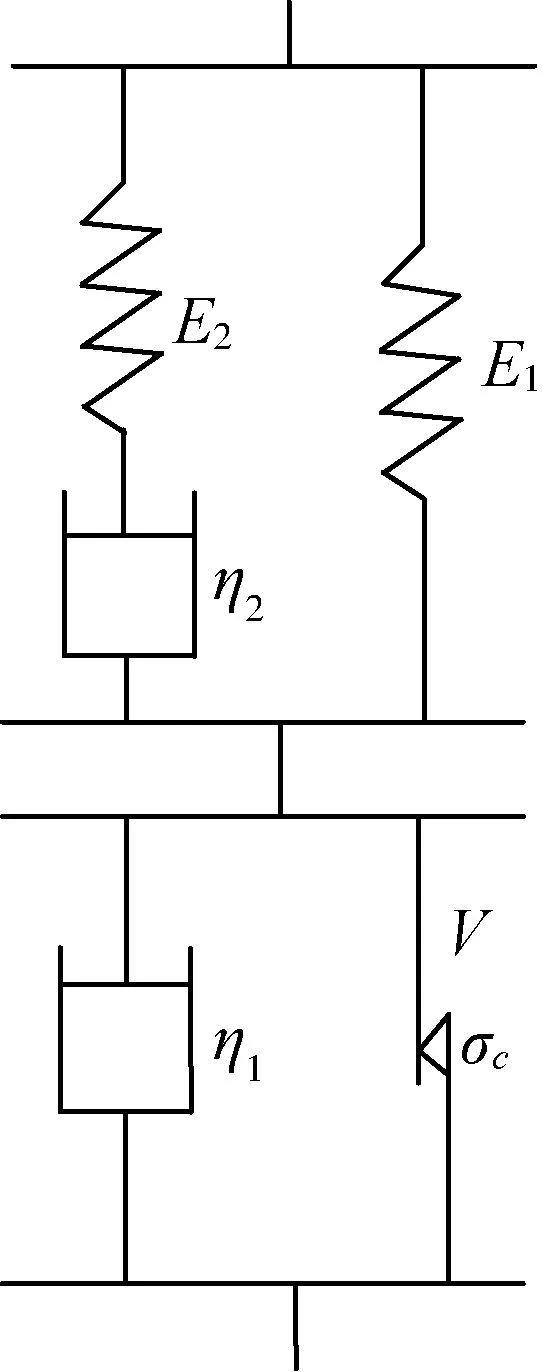
图3 非线性黏弹塑性模型Fig. 3 Nonlinear viscous-elastic-plastic model
经拉普拉斯变换和逆拉普拉斯变换,第Ⅱ阶段应力σ2与时间t的函数关系见式(4)。
(4)
其中,
3) 第Ⅲ阶段。在高应力作用下原棉的力学特性由非线性黏弹塑性转变为高级黏弹性,其力学模型与图2一致,第Ⅲ阶段应力σ3与时间t的函数关系见式(5)。
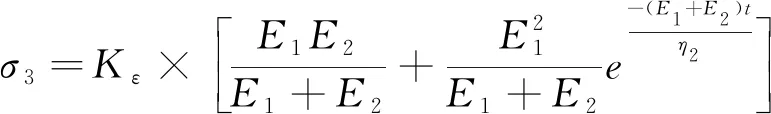
(5)
4) 回复阶段。原棉回复特性由弹性变形和少量黏弹组成,其力学模型亦可采用黏弹力学模型,回复阶段应力σ4与时间t的函数关系见式(6)。
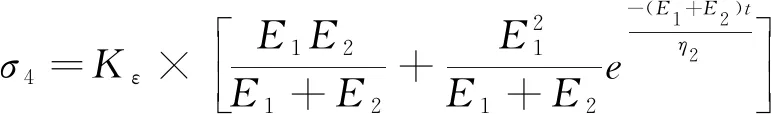
(6)
4 模型参数确定
原棉的各阶段应力与时间函数关系式中,包含了E1、E2、η1、η2四个力学模型参数。为了模拟计算力学参数,对函数关系式进行简化。
第Ⅰ、Ⅲ阶段、回复阶段的函数关系式简化为
(7)
其中,
第Ⅱ阶段的函数关系式简化为
(8)
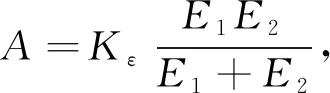
将图1的应力与应变数据转化为应力与时间数据,再分阶段进行非线性曲线拟合,结果如表1所示。
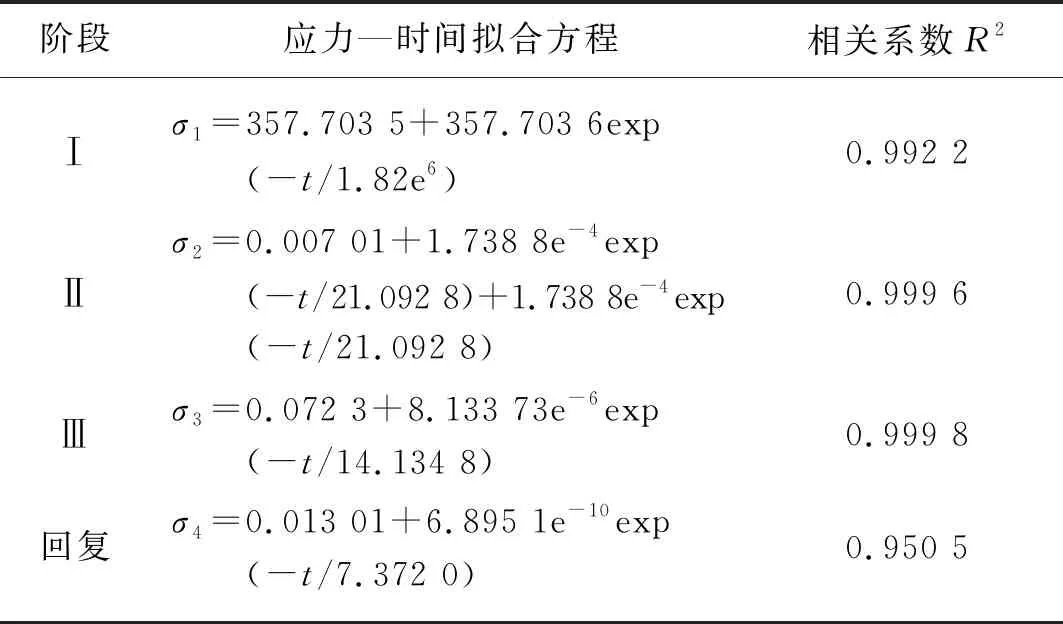
表1 原棉压缩回复应力—时间拟合方程Tab. 1 Stress-time curve fitting functions of compression and
由表1可知,第Ⅱ阶段的拟合方程的B与D、C与F参量均相等,表明第Ⅱ阶段应力与时间数据特征与其他各阶段是一致的。该阶段原棉压缩变形仍以黏弹性变形为主,其黏塑性变形较少。E1、E2、η2可定量分析原棉压缩-回复的黏弹力学行为;η1表征黏塑性变形,黏滞系数η1值无法获得,亦表明原棉的黏塑性变形极为微弱。因此,原棉压缩-回复各阶段的应力与时间的拟合方程均为σ=a+b×exp(t/c),其相关系数R2均大于0.95,且拟合效果极佳。故非线性黏弹性模型能较好地表征原棉各阶段力学过程。依据原棉的应力与时间拟合方程计算出各阶段的E1、E2、η23个力学参数,其计算公式如式(9)~式(11)。
(9)
(10)
η2=-c(E1+E2)
(11)
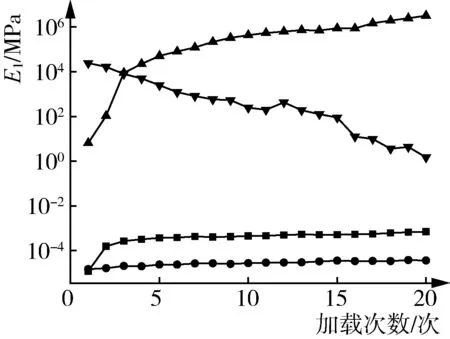
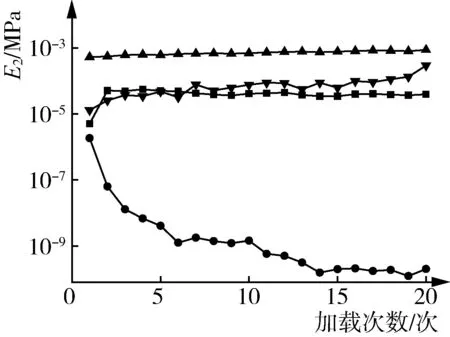
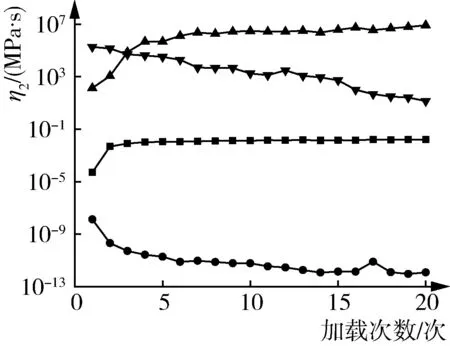
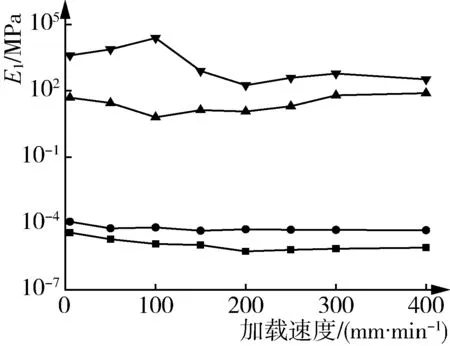
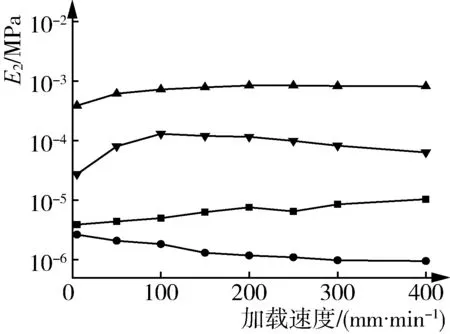
在循环加载、不同加速度和不同回潮率条件下加载原棉,其各阶段的E1、E2、η2值,见图4~图6。对比图4、图5、图6,发现各阶段E1、η2曲线变化规律极为相近。Ⅰ、Ⅱ、Ⅲ、回复阶段的E1值均大于E2值。由此可见,原棉压缩期间黏性、弹性并行。
(a) E1 (b) E2 (c) η2
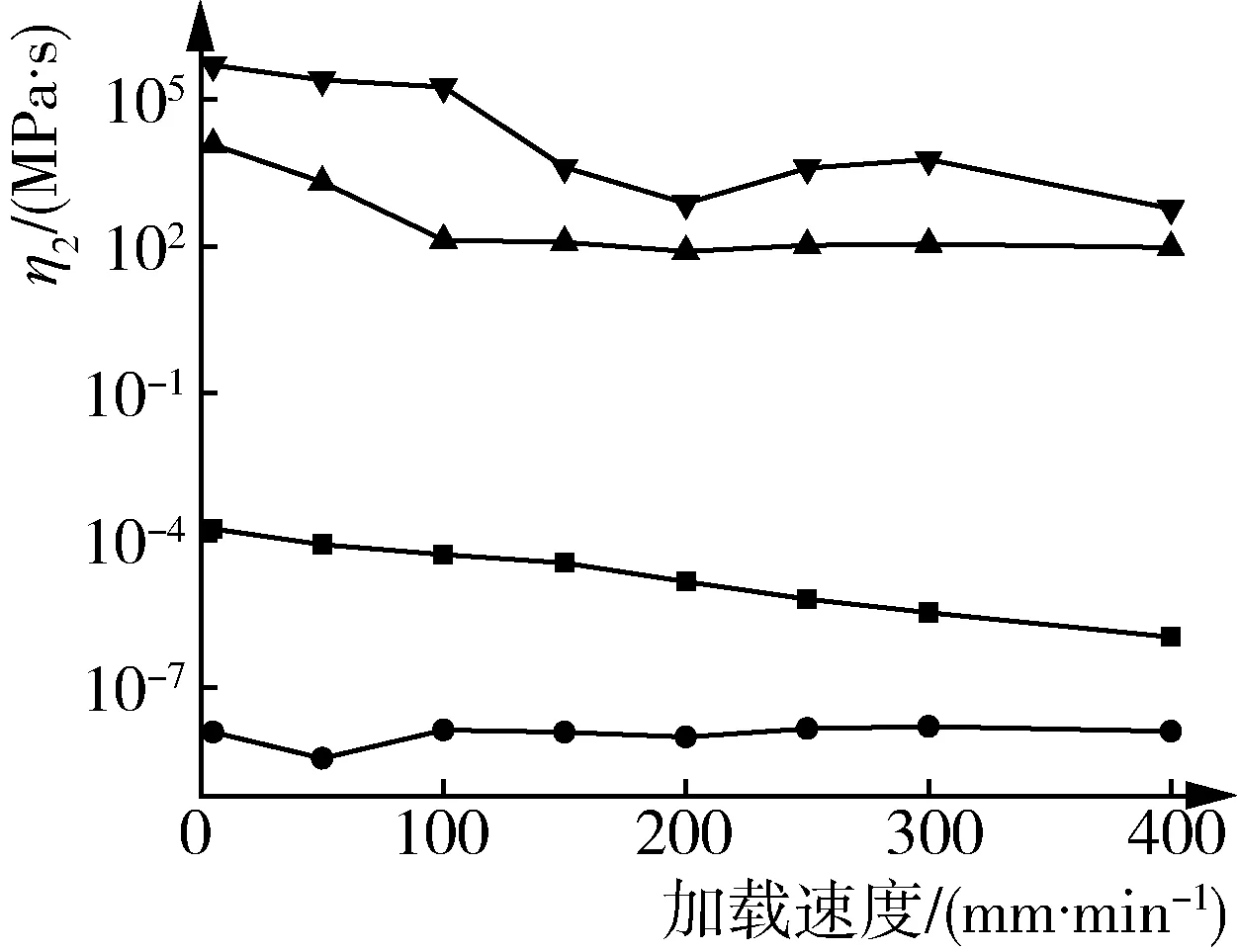
(a) E1 (b) E2 (c) η2
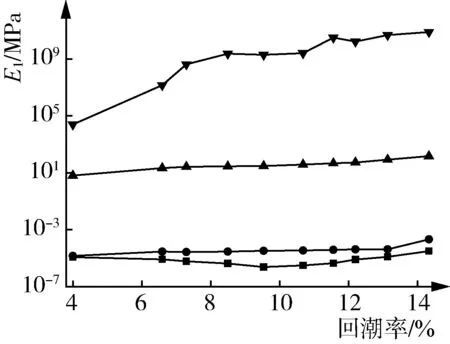
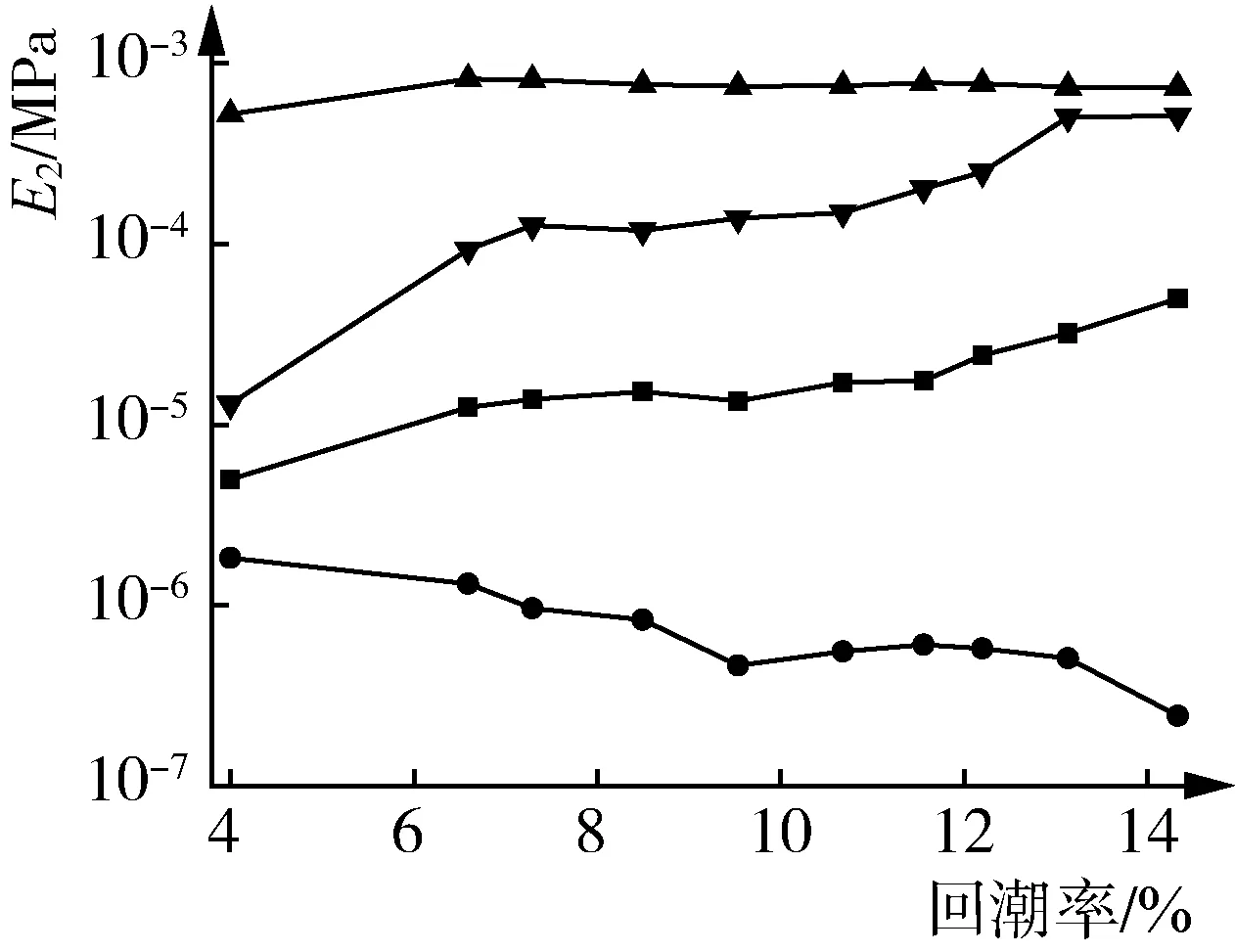
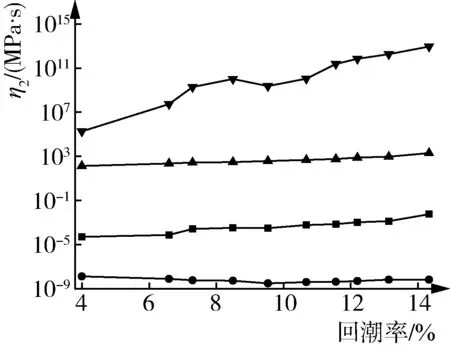
(a) E1 (b) E2 (c) η2
5 模型参数影响因素分析
5.1 循环加载
循环加载原棉,其各阶段的E1、E2、η2值见图4。由图4可知,随着加载次数的增加,Ⅰ、Ⅱ、Ⅲ阶段的E1值增大,回复阶段E1值减小。表明Ⅰ、Ⅱ、Ⅲ阶段原棉的弹性模量上升,材料的压缩刚性加强;回复阶段E1值弹性模量下降,材料的弹性加强。随着加载次数的增加,Ⅰ、Ⅲ、回复阶段的E2值增大,Ⅱ阶段E2值减小。表明Ⅰ、Ⅲ、回复阶段原棉的黏弹性模量上升,材料的黏弹性减弱;Ⅱ阶段原棉的黏弹性模量下降,材料的黏弹性加强。Ⅰ、Ⅲ阶段的η2值增大,Ⅱ、回复阶段的η2值减小。表明Ⅰ、Ⅲ阶段原棉的黏度系数上升,材料的黏性减弱;Ⅱ、回复阶段原棉的黏度系数下降,Ⅱ、回复阶段材料的黏性加强。各阶段E1和η2值的变化规律相近,体现了原棉黏性与弹性并存。每次加载,压力均有助于原棉内部纤维滑移,致使其黏弹性能降低、塑性变形积累。故循环加载原棉有助于其排空内部空隙,促进原棉致密化,降低了原棉的黏性和弹性。
5.2 加载速度
不同加载速度压缩原棉,其各阶段的E1、E2、η2值见图5。由图5可知,随着加载速度的增加,Ⅰ、Ⅱ阶段的E1值变化不显著,Ⅲ阶段的E1值先减小后增大;回复阶段的E1值先增大后减小;Ⅰ、Ⅲ阶段的E2值均增大,Ⅱ阶段E2值减少,回复阶段E2值先增大后减小;Ⅰ、Ⅲ阶段的η2值均逐渐减小,Ⅱ、回复阶段的η2值无显著变化,表明加载速度增高会降低材料的黏性。各阶段E1、E2、η2值的变化规律均不相似。加载速度大于200 mm/min后,原棉各阶段的E1、E2、η2值趋于稳定。加载速度对原棉的力学参数的影响不显著,其未能对原棉内部纤维运动起关键作用。
5.3 回潮率
恒速压缩不同回潮率的原棉,其各阶段的E1、E2、η2值见图6。由图6可知,随着回潮率的增加,各阶段的E1、η2值均增加,Ⅰ、Ⅱ、Ⅲ阶段的E1、η2值变化幅度较小,回复阶段的E1、η2值变化幅度较大。表明原棉的弹性模量和黏度系数均上升,材料的弹性、黏性均下降。Ⅰ、Ⅲ、回复阶段的E2值均增加,Ⅱ阶段的E2值减少。表明Ⅰ、Ⅲ、回复阶段原棉的黏弹性模量均上升,材料的黏弹性性能下降;Ⅱ阶段原棉的黏弹性模量下降,材料的黏弹性有增强趋势。回潮率对原棉的力学参数的影响较为显著。棉纤维回潮率高,其表面携带的自由基水分子含量高,使棉纤维更柔韧易于弯曲[15]。棉纤维表面附着的水分子加强纤维间摩擦作用引发黏滞效应。同时,水分子也易进入棉纤维的无定形区,引起棉纤维横向膨化,增强纤维间抱合力。在压力作用下,高回潮率原棉的形态结构更易于由黏流态向近固态转变。
6 结论
1) 利用万能试验机压缩亚克力圆筒内的原棉,获得原棉压缩-回复的应力应变曲线,其压缩和回复曲线存在显著滞后性,且压缩曲线分3个阶段。分析压缩应力—应变曲线发现:原棉压缩性能呈现出非线性的黏弹性、黏塑性,压缩过程以黏弹性为主,回复过程以弹性为主。
2) 基于黏弹塑性理论,分阶段建立原棉的黏弹塑性力学模型,其可表征原棉的非线性黏弹性力学性能。各阶段,原棉的应力与时间函数关系式均可简化为σ=a+b×exp(t/c),通过试验数据拟合可获得原棉模型中弹性元件的弹性模量E1、黏性元件的弹性模量E2、黏性元件的黏性系数η23个参数值,且拟合效果极佳。
3) 对比不同加载次数、加载速度、回潮率条件下原棉的E1、E2、η2值,发现加载次数、回潮率对原棉的E1、E2、η2的3个力学参数较为显著。多次加载可促进原棉致密,减弱原棉的弹性和黏性。高回潮率原棉受压易于致密固结。控制压缩参数,可降低原棉压缩与开松机械加工能耗,减少原棉加工损伤。

