部分相干圆偏振反常涡旋光束的紧聚焦及辐射力研究

董 淼,姚 骏,白毅华

(电子科技大学物理学院,四川 成都 610054)

1 引 言

近年来,光束的紧聚焦特性成为研究热点[1-7]。研究人员发现光束经过紧聚焦后形成各类光斑,光斑性质与入射光场密切相关。比如,径向偏振光可以产生一个很强的纵向光场,并且比线性光束更加容易聚焦形成紧凑的点。目前通过径向偏振光可形成极小的聚焦光斑[8-9]。角向偏振光束经过紧聚焦后在焦平面处呈现空心强度分布且偏振方向保持不变[10-11]。柱矢量光束经过紧聚焦后通过变化偏振角可以对光强分布进行整形,形成空心、实心,平顶光束等[12-13]。这些特殊性质可以广泛应用于多种领域,如高分辨成像,光学数据存储,光学捕获以及材料加工、处理等[8-13]。

另一方面,涡旋光束由于具有奇异的光学性质,受到人们的广泛关注[14]。起初,研究人员主要关注均匀偏振涡旋光束的相位和振幅的光学奇异性,即所谓的标量涡旋光束。近年来,研究人员开始关注非均匀偏振矢量涡旋光束。基于柱矢量坐标系下的圆偏振涡旋光束,将标量与矢量涡旋连接在一起,成为很好的研究对象[15]。此外,圆偏振涡旋光束同时携带自旋角动量(与圆偏振有关)和轨道角动量(与涡旋相位有关),有利于研究光子的力学性质与本质[16]。因此,不少研究团队开展了圆偏振涡旋光束的紧聚焦特性研究[17-19]。比如,Zhao等人发现经过紧聚焦后圆偏振涡旋光束所携带的自旋角动量可以转换为轨道角动量[17]。但是,目前圆偏振涡旋光束的紧聚焦特性研究主要集中在完全相干光,对于部分相干光束的研究还比较少。因此,本文以部分相干圆偏振反常涡旋光束为研究对象,利用Richard-Wolf矢量衍射积分理论及部分相干理论,推导了该光束紧聚焦后总的光强以及x,y,z三个分量的光强表达式。讨论了拓扑荷数、光束阶数、相干长度、数值孔径大小对于总光强及各分量光强的影响。利用瑞利散射理论,研究了部分相干圆偏振反常涡旋光束对金属瑞利粒子的辐射力。研究结果对光束的传输变换以及在光镊中的应用具有重要作用。

2 理论模型

反常涡旋光束在源场处的电场振幅分布表示为[20]:

exp(-imθ)

(1)

其中,E0为常数;m,n分别为拓扑荷数和光学阶数;w0为束腰宽度,(r,θ)为源平面上某点的径向和角向坐标。当m=n=0时,光束为高斯光束；当m=0,n≠0时,光束为空心高斯光束；当m≠0,n=0时,光束为高斯涡旋光束。

将完全相干光推广到部分相干光中[21],部分相干反常涡旋光束在源点处的交叉关联函数可以表示为:

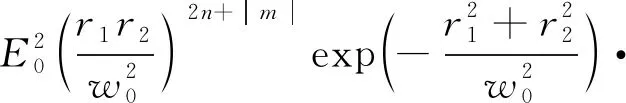
(2)

经过紧聚焦后,一般透镜符合正弦条件,即r=fsinθ。将正弦条件代入公式(2),那么部分相干反常涡旋光束的切趾函数可以表示为:

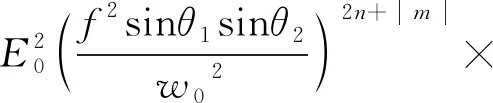
(3)

一束完全相干圆偏振光束经过高数值孔径聚焦后的结构图如图1所示。根据文献[22],在焦平面处的圆偏振光束的光强表示为:

(4)

其中,(r,φ,z)为柱坐标系下观察平面上任意一点的坐标。θ为数值孔径的角度,取值从0到α,其中α=arcsin(NA)。φ为入射光束的方位角。k=2π/λ为波数,λ为波长。f为透镜的焦距。P(θ,φ)为光澜处的切趾函数。

图1 紧聚焦系统结构图

经过运算将公式(4)进行化简,得到光场在x,y和z分量的表达式[22]:

[(1+cosθ)imJm(krsinθ)exp(imφ)+(cosθ-1)·

im±2Jm±2(krsinθ)exp[i(m±2)φ]dθ

(5)

[±i×(1+cosθ)imJm(krsinθ)exp(imφ)∓

i(cosθ-1)im±2Jm±2(krsinθ)exp[i(m±2)φ]dθ

(6)

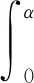
im±1Jm±1(krsinθ)exp[i(m±1)φ]dθ

(7)

其中,“+”代表右旋圆偏振光,“-”代表左旋圆偏振光束。

根据部分相干理论,部分相干圆偏振涡旋光束的交叉谱密度可以表示为:

Wij(r1,r2,z)=〈Ei*(r1,φ1,z)Ej(r2,φ2,z)〉,(i,j=x,y,z)

(8)

其中,r1,r2分别为观察平面的任意两点位置。将公式(3)、(5)～(7)代入到公式(8)中,可以得到观察平面的部分相干圆偏振反常涡旋光束的交叉谱函数。当r1=r2=r,φ1=φ2=φ时,可以得到部分相干圆偏振反常涡旋光束在焦平面处总光强表达式:

It=Wxx+Wyy+Wzz=Ix+Iy+Iz

(9)

3 紧聚焦特性的仿真

图2 不同拓扑荷数下部分相干左旋圆偏振

图3给出了不同拓扑荷数下部分相干右旋圆偏振反常涡旋光束的紧聚焦后的光强分布。从图中可以看出,在m=0时,光强分布与左旋圆偏振情况相似。随着拓扑荷数增加,总光强以及x,y,z分量的光强均为空心分布并且暗中空区域不断增大。x,y分量光强分别沿着x轴,y轴方向被拉伸,形成了椭圆状分布,与左旋情况刚好相反,如图3(b)、(c)所示。z轴方向分量的暗中空区域是由于右旋圆偏振涡旋光束携带自旋角动量ħ和轨道角动量lħ。当经过紧聚焦后,自旋角动量转换为轨道角动量ħ,从而使z分量光束携带了轨道角动量(l+1)ħ。

图3 不同拓扑荷数下部分相干右旋圆偏振反常涡旋

图4给出了光学阶数n对于部分相干圆偏振反常涡旋光束紧聚焦的影响。其他参数如图3所示。从图中可以看出,光学阶数不改变左旋或右旋圆偏振光束的光强分布。

图4 不同光学阶数对部分相干圆偏振

图5给出了不同相干长度对部分相干圆偏振反常涡旋光束紧聚焦后的光强分布影响。参数m=1,n=1,NA=0.7,其他参数如图4所示。从图中可以看出,无论左旋还是右旋圆偏振涡旋光束,相干长度越大,光强值越大,相干长度不改变光强的分布。

图6给出了不同数值孔径(NA)对紧聚焦后光强分布的影响。参数如下:m=1n=1w0=2 cm,f=1 cm,δ=w0。对于左旋情况,当NA从0.7增加到0.9,焦平面处光强分布逐渐从暗斑分布变为

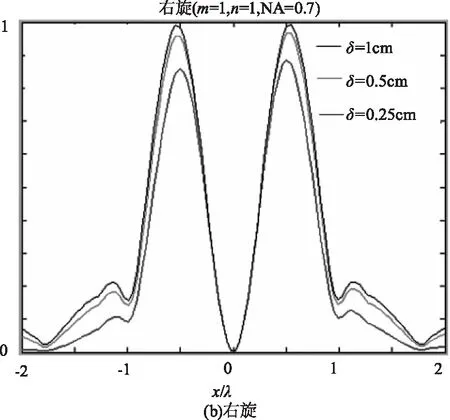
图5 不同相干长度对部分相干圆偏振反常

高斯分布,光斑更加聚焦,光强值增大。也就是说,调整NA的大小可以对光强分布进行整形。对于右旋情况,当NA从0.7增加到0.9,光强分布始终保持为暗中空分布,光强值逐渐增加,光斑更加聚焦。

4 光束对金属瑞利粒子辐射力理论仿真

随着光镊技术的发展,光镊的捕获对象也从普通的绝缘介质粒子拓展到了金属粒子。与一般的绝缘介质不一样,金属粒子由于具有更好的化学活性,在化学、生物中起到很好的催化效果,具有广泛的应用价值[23]。金属粒子的介电常数表示为εm=ε1+iε2,与波长有关。由于介电常数存在着虚部,因此将产生一个与散射力相比拟的吸收力,方向与散射力相同,因此很难被捕获[24]。目前通过光场调制提供足够的梯度力来克服散射力及吸收力是对金属粒子捕获的一种途径。本节将进一步研究部分相干圆偏振反常涡旋光束对金属瑞利粒子的辐射力。

“一带一路”沿线65个国家中有53种官方语言。[15] 目前中国大多数高校为非英语专业学生开设的语种主要是英语，只有北京外国语大学和上海外国语大学能够开设一些非通用语种。 造成这一现象的原因很多，最主要的是师资的匮乏，短时期很难培养出非通用语种的教师。 因此，英语作为全球通用语在很长一段时间仍是我们进行跨文化交际最主要的语言工具。 面对这样的困境，对“一带一路”沿线国家文化知识的输入就显得尤为重要，跨文化交际中除了语言交际外，还有非语言交际和超语言交际，极大地利用好这两种交际方式可以弥补语言交际上的不足，仍然可以顺利地实现跨文化交际。

根据偶极子近似,金属瑞利微粒受到的力分为:梯度力,散射力和吸收力,分别表示为[25-26]:

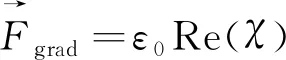
(10)

(11)

(12)

其中,E为电场矢量;Cscat为散射截面;Cabs为吸收截面;χ为粒子的极化率;I(r,z)为出射光强。分别表示为:

(13)

(14)

(15)

(16)

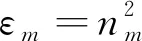
根据以上公式,我们计算部分相干左旋圆偏振反常涡旋光束紧聚焦后对金属瑞利粒子的捕获力。参数选择如下:λ=1047 nm,ε′=-54+5.9i,w0=10 mm,a=20 nm,δ=ω0,f=1 mm,w0=1 mm,nm=1.33,ε0=8.85 pN,δ=w0,NA=0.95。

图7给出了不同拓扑荷数下部分相干左旋圆偏振反常涡旋光束经过紧聚焦后在焦平面对金属瑞利粒子产生的辐射力。此时的光学阶数n=1。

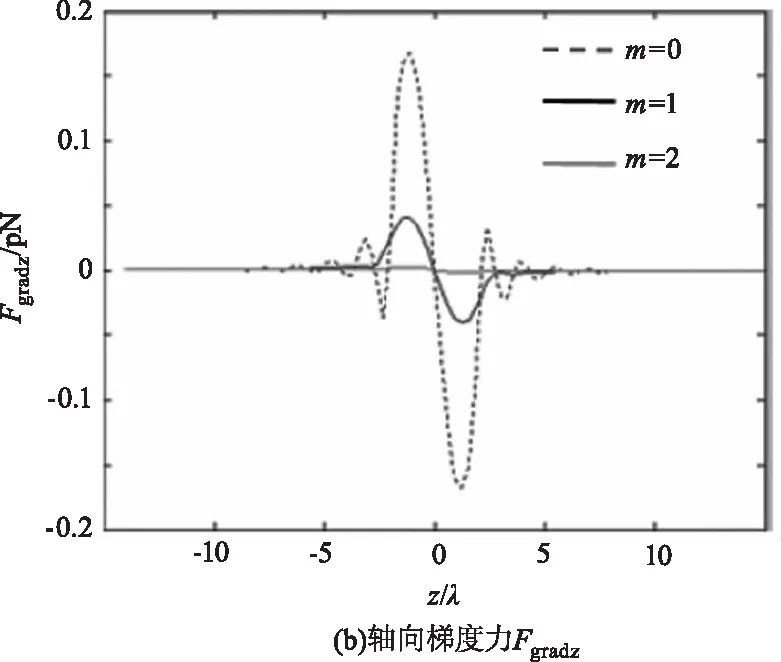
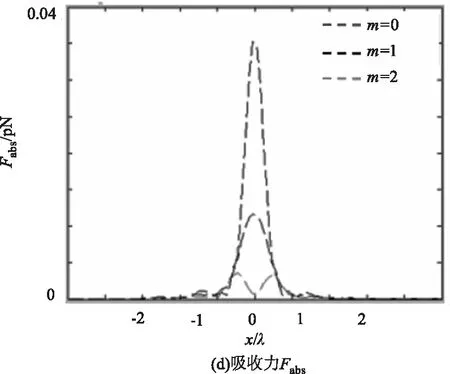
图7 不同拓扑荷数下部分相干左旋圆偏振反常涡旋光束紧

从图可以看出,当拓扑荷数m≤1时,横向、轴向梯度力存在一个稳定的平衡点,并且轴向的梯度力大于散射力与吸收力之和。因此,金属微粒可以被捕获。当拓扑荷数m>1,光强分布从实心转为空心,横向和轴向梯度力在中心无稳定的平衡点,并且辐射力减少,因此无法在轴上进行稳定捕获。

图8给出了不同光束阶数下该光束对金属瑞利粒子的辐射力。从图中可以看出,随着光束阶数n的增大,梯度力、散射力、吸收力均减少。因此,我们可以调节光束阶数来改变对金属瑞利粒子的辐射力。

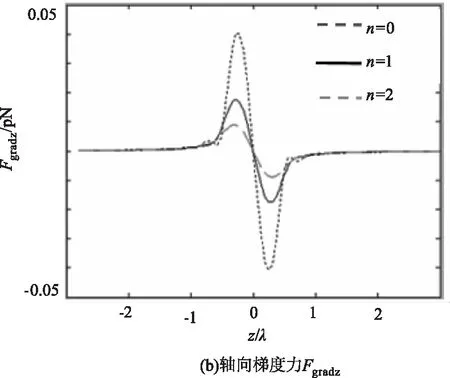
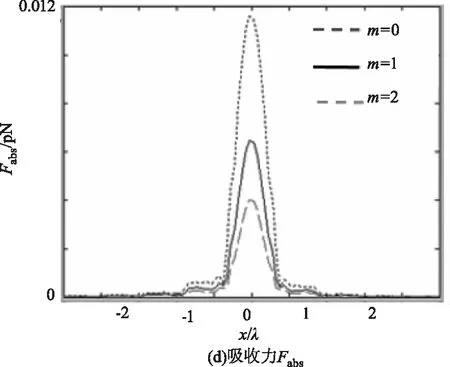
图8 不同光束阶数下,部分相干反常涡旋

为了能够稳定捕获微粒,纵向的梯度力必须大于散射力与吸收力之和。从图7、8可知,纵向梯度力远大于散射力和吸收力之和。为了进行稳定的捕获,必须考虑布朗运动的影响,这就要求梯度力产生的最大势阱必须克服粒子的动能,这个条件用玻尔兹曼因子来进行描述[26]:

Rthermal=exp(-Umax/kBT)≪1

(17)

其中,kb表示玻尔兹曼常数;Umax=Re(χ)ε0Imax/2,T=300 K。

当粒子尺寸a=20 nm时,玻尔兹曼因子为2.43×10-20,远远小于1,因此梯度力可以克服粒子的动能。除此以外还需要考虑金属的重力影响,金的密度为19.32×103kg/m3,半径为20 nm的金属粒子所受的重力为6.5×10-7pN,梯度力与散射力远远大于重力。因此可以利用该光束实现对金属瑞利粒子进行稳定捕获。

5 结 论

本文根据Richard-Wolf矢量衍射积分理论以及部分相干理论,推导了部分相干圆偏振反常涡旋光束紧聚焦后的光强表达式。讨论了拓扑荷数、光束阶数、相干长度、数值孔径大小对于紧聚焦后焦平面处总光强及各个分量光强分布的影响。研究结果表明,自旋方式,拓扑荷数以及数值孔径对光强分布产生影响。光束阶数,相干长度仅对光强值产生影响。因此,通过调节不同的光学参数可以实现对光强的整形。利用瑞利散射理论,研究了部分相干圆偏振反常涡旋光束经过紧聚焦后对金属瑞利粒子的辐射力。研究结果表明,低阶拓扑荷数以及光学阶数的部分相干左旋圆偏振反常涡旋光束紧聚焦后形成的实心光强分布可以对金属瑞利粒子进行捕获。结果对光束的传输变换以及光镊应用具有重要的理论价值。