基于激光雷达的有界区域快速全局定位算法

吴海欣,文梓豪,熊弘俊,崔 彦,林军记,张 辉

(1.中山大学智能工程学院,广东 广州 510006；2.广东省智能交通系统重点实验室,广东 广州 510006)

1 引 言

精准定位是自动驾驶、无人机器人等一系列重要应用的基础,分为室外定位和室内定位。在室外环境下,全球导航卫星系统(global navigation satellite system,GNSS)可以提供精确的位置信息[1],但在像停车场等的一些室内环境以及像隧道等被严重遮挡的室外环境下,其定位精度已无法满足我们的定位精度需求。因此,近年来国内外各界都在致力寻求更高精度和可靠的室内定位技术,使之在特定环境条件下也可以获得准确的位置信息。

目前,国内外的室内定位领域主要包括有射频识别(RFID)[2]、Wi-Fi、ZigBee、超宽带(UWB)、惯性导航、超声波[3]、激光、红外线、蓝牙[4]等定位技术。这些定位技术的区别在于其传感器和数据传输方式的不同,而其后台核心定位算法才是对定位效果起关键作用的因素,包括有邻近信息法、多边测量法、双曲线定位法、三角定位法、指纹定位法和航位推算法等。就目前的技术发展而言,每个定位技术都有其优点和局限性,不具有同时满足定位精度、成本、功耗和信息安全多个方面的普适性技术。与此同时,不同的定位算法所适用的定位技术不同,因此各界也在致力寻求一种可靠、稳定的定位技术与算法的结合,实现室内定位精度和功耗等方面的最佳化。

另一方面,室内定位作为机器人必不可少的一个关键技术,可以分为位置跟踪和全局定位两类。位置跟踪是指在已知初始位姿以及未知地图的前提下,对运动状态下的机器人进行定位,如激光SLAM定位[5]和视觉SLAM定位[6]。但SLAM定位技术不可避免地会产生随着车辆里程的增大而增大的累积误差。相对而言,全局定位则要求在对初始位姿没有任何先验知识和已知地图的情况下,获取当前时刻机器人的位置信息。基于已知地图的全局定位与SLAM不同,其过程是将当前时刻采集到的环境点云与事先建好的地图作匹配,每次帧间配准相对独立,所以其不存在累积误差[7]。当然全局定位也更具难度和挑战性,目前主要有全局视觉定位[8]和基于激光雷达的全局定位[9]等。

由于基于摄像机的全局定位会受到光照因素的影响,相比而言激光雷达则具有不受环境光影响以及精度更高的优势,本文以激光雷达为单一的传感器,提出一种室内有界区域下的快速全局定位算法,将激光定位技术与全局定位算法有效地结合,并在仿真实验下取得可靠、稳定的定位效果。

2 问题的描述

全局定位实际上是一个坐标转换的问题,其过程就是建立地面坐标系与车辆坐标系之间的对应关系[10]。在本文的研究中,地面坐标系是不变的、绝对的,而车辆坐标系是随着车辆位姿的变换而变的。因此,地面坐标系下的全局地图也是不变的。但在雷达实时定位建图过程中,智能车需要构建环境地图,用于对自身的精确定位,而环境地图的构建又与智能车在每个时刻的位置息息相关[11],即车辆坐标系中的局部地图也将随着车辆位姿的变换而改变。因此,要实现激光雷达的全局定位,就要将变换的车辆坐标系下的局部地图和绝对的地面坐标系下的全局地图进行匹配,最终得出车辆在地面坐标系下的位姿,包括其坐标以及方向角。

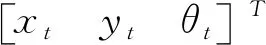
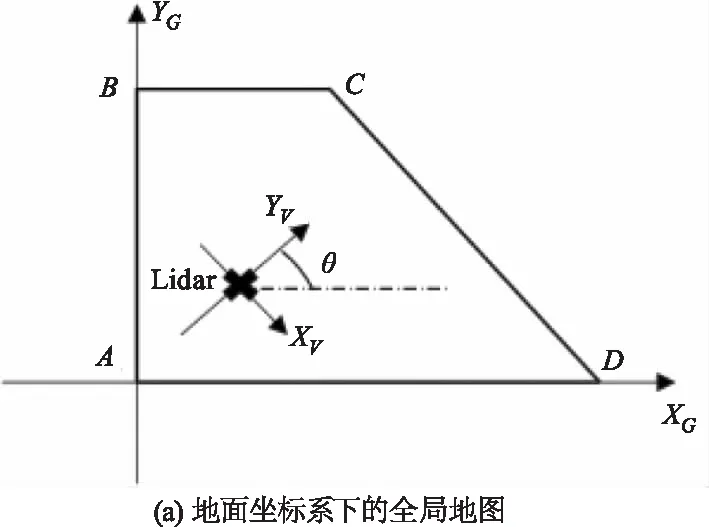
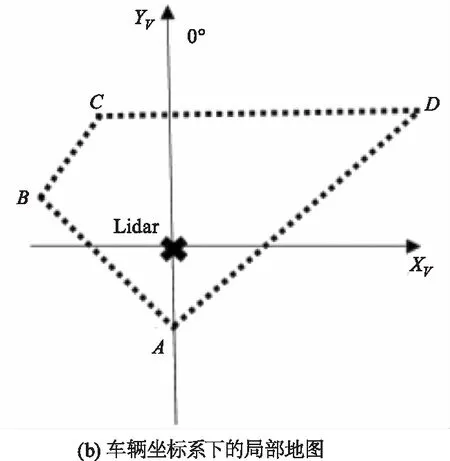
图1 坐标系转换关系

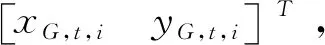
(1)

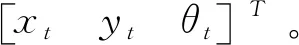
3 地图的特征描述

在地图只有边界的情况下,任意一个凸多边形地图都可以采用一个特征向量来对其进行描述,每个凸多边形对应特定且唯一的特征向量。该特征向量我们定义如式(2)所示。

V=[Xg,Yg,Lmax,αmax,Lmin,αmin,

L1,α1,L2,α2,L3,α3,…]T

(2)

其中,Xg,Yg为地图边界的重心坐标;Lmax,αmax分别表示重心到最远点的距离和方向角;Lmin,αmin分别表示重心到最近点的距离和方向角。αi,Li为αmax,αmin之间分割出来的第i个角及重心到该方向角上边界点的距离。

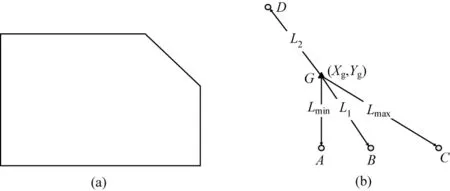
图2 凸多边形地图特征描述

4 定位算法

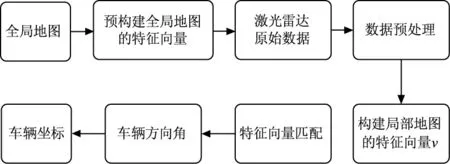
图3 全局定位算法流程

4.1 预构建全局地图特征向量

在已知地图和已知地面坐标系的情况下,首先需要构建出全局地图的特征向量V=[Xg,Yg,

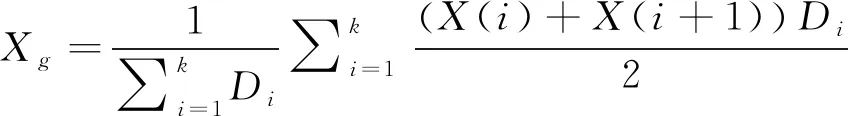
(3)

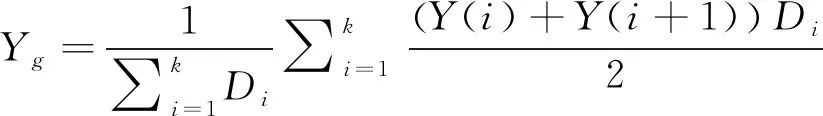
(4)

其中,X(i),Y(i)(i=1,2,3,…,k)表示凸多边形地图第i个顶点的全局坐标;Di表示第i个顶点与其下一个顶点的欧氏距离。

4.2 数据扫描与预处理

激光雷达通常采用飞行时间法测距,即通过测量从发射激光脉冲到接收发射光的时间间隔,根据光的行程和飞行时间计算距离[12],如式(5)所示。

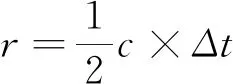
(5)

式中,r表示目标距离;Δt表示发射波与反射波的时间延迟,光速c=3×108m/s。

当二维单线激光雷达处于地图区域内时,实时地对地图的边界进行扫描,采集到地图边界的n组离散的点云数据,包括n个边界点到雷达的距离和角度。采集完点云数据后,数据预处理基本流程如图4所示。

图4 数据预处理基本流程图

大部分激光雷达的测距范围都有一定的阈值,当雷达靠近或者远离地图边界时会出现部分边界点的距离数据为0等异常的情况,所以首先要识别并剔除该部分异常数据。同时值得注意的是,激光雷达的飞行时间法测距本身也存在误差,包括有系统误差和噪声误差。其中系统误差包括计时误差、时刻鉴别误差以及大气折射率误差,而随机误差则主要是噪声引起的误差[13]。因此,在剔除异常数据外,还需要对点云数据的误差进行校正。

校正误差后,由于激光雷达所获取的点云是极坐标数据,而在后续定位中需要用到的是直角坐标数据,因此需要将点云数据转换为其在车辆坐标系下的直角坐标数据,构建局部地图。其转换公式如式(6)所示:

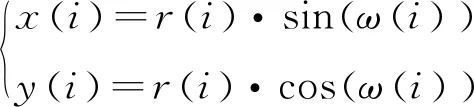
(6)

式中,x(i),y(i)表示扫描到的第i个边界点在车辆坐标系中的横坐标和纵坐标;r(i)表示该点到激光雷达的距离数据;ω(i)则表示该点的角度数据。

4.3 构建局部地图特征向量

对数据进行预处理并构建局部地图后,要对局部地图进行特征提取,提取局部地图重心到最远点的距离lmax和方向角βmax,重心到最近点的距离lmin和方向角βmin,以及βmax,βmin之间分割出来的第i个角βi和重心到该方向角上边界点的距离li。其中,局部地图重心坐标xg,yg可由式(7)～(9)解得:

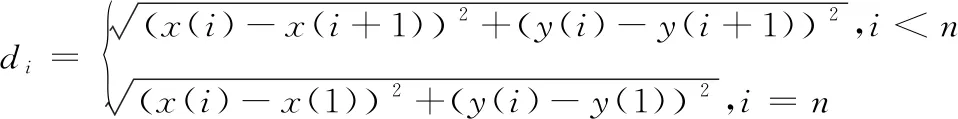
(7)

(8)

(9)

式中,di(i=1,2,…,n)表示局部地图中相邻两个边界点的距离。

由此,提取出局部地图中的特征信息(如重心坐标、重心与边界点的距离以及方向角)后,可以构建出局部地图在车辆坐标系中的特征向量v,如式(10)所示:

v=[xg,yg,lmax,βmax,lmin,βmin,

l1,β1,l2,β2,l3,β3,…]T

(10)

4.4 特征向量匹配定位

(11)

(12)

该算法提取激光雷达采集的点云数据特征,将其与数据库中事先存储的全局地图特征数据进行匹配,只需找出全局地图与局部地图中一个对应的特征点——重心,并利用重心与特定边界点的方向角,最终实现车辆在有界区域内的快速全局定位,大大减少了计算量,从而降低了定位算法的复杂度。

5 非凸多边形切分

值得注意的是,当机器人处于非凸多边形地图内,激光雷达位于某些特定区域时会出现被地图边界遮挡而漏扫的现象,构建出不完整的局部地图,这可能导致两个坐标系中地图边界的重心不是一一对应的特征点,因此无法直接将局部地图与全局地图进行特征向量匹配。此时需要对地图进行图形切分,再运用改进后的边界特征匹配方法来进行定位。

本文的图形切分原则为,将原非凸多边形地图看作多个凸多边形的叠加组合,并根据这些凸多边形的重合情况来切分地图。如图5所示的非凸多边形地图ABCDEF,可将其视为凸多边形ABCG与凸多边形AHEF的叠加组合,此时根据其重合的情况可将地图内切分为①,②,③三个区域。

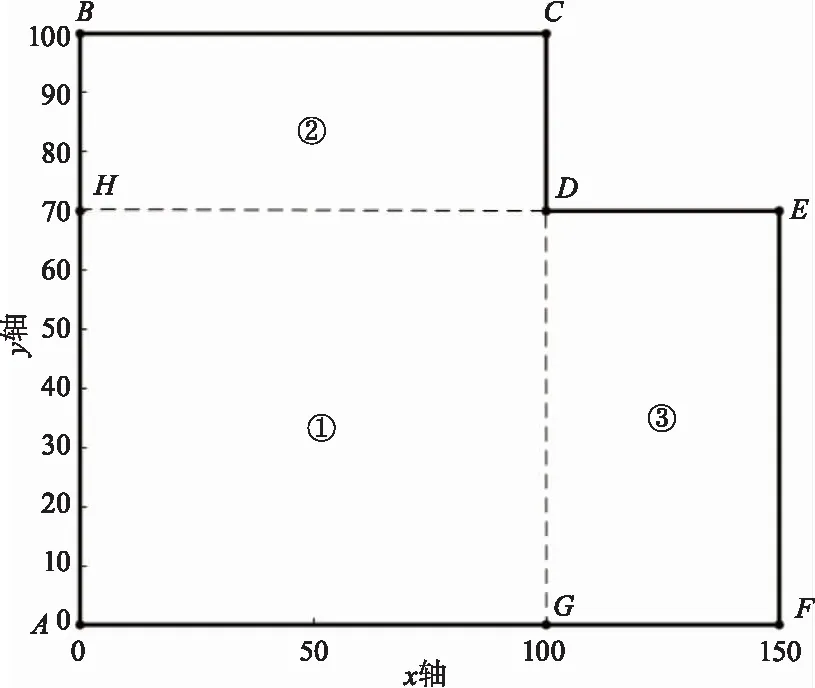
图5 非凸多边形图形切分

雷达在不同的区域中只能完整地识别出其所在凸多边形与原地图的交集部分。如当雷达处于区域②时,其所属的凸多边形ABCG与原地图的交集为多线段GABCD,此时雷达可以完整扫描出该多线段,但受顶点D的影响无法完整扫描出线段DEFG,区域①③同理。

改进后的特征匹配方法解决了非凸多边形地图内雷达会出现漏扫的现象,其具体步骤如下所示:

Step 1:非凸多边形地图可视为多个凸多边形的叠加组合,计算这些凸多边形与原地图边界的交集的特征向量Vi;

Step 2:计算激光雷达扫描的点云图中每相邻两个点的距离di以及地图上的最短边长Dmin,判断是否存在di>Dmin。若不存在,则雷达点云图无漏扫,按照凸多边形地图定位方法进行定位；若存在,则雷达点云图存在漏扫,跳至步骤3；

Step 3:在雷达点云图中剔除不能完整扫描出的多线段部分,保留可完整扫描出的多线段部分；

Step 4:计算此时点云图的特征向量v以及|Vi-v|。将Vm中的参数带入式(11)和式(12)中计算得出车辆位姿。其中|Vm-v|=min(|Vi-v|)。

6 实验验证

为了高效地验证本文算法的有效性及其定位精度,本文在进行全局定位测试时,将预设好的有界多边形地图导入,在MATLAB上通过仿真实验模仿不同位姿时二维单线激光雷达在地图内的扫描过程,并运用本文提出的全局定位算法解算出车辆的坐标和朝向。

本文定位误差的评估通过位置误差比和朝向误差来描述。位置误差比的定义如式(13)所示:

(13)

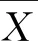
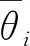
(14)

由于非凸多边形地图可通过图形切分为多个区域,既可以验证凸多边形快速定位算法又可以验证改进后的特征匹配方法,因此本次实验选取了图5中的有界非凸多边形为实验地图,该地图具有代表性。

本次实验的位置误差状况如图6所示。由图6(a)可知雷达在无漏扫区域时整体误差较小,而当雷达处于漏扫区域时位置误差比有所增大。由图6(b)可知本次实验雷达采用的3251个位置中,92.7 %以上的位置误差比小于1.9 %,平均位置误差比为0.791 %。

而本次实验的朝向误差状况如图7所示。由图7(a)可知雷达在无漏扫区域时整体误差较小,而当雷达处于漏扫区域时朝向误差有所增大,该特点与位置误差一致。由图7(b)可知采用的3251个样本点中,94.2 %以上的朝向误差小于1°,最小朝向误差几乎为0,而平均朝向误差为0.3883°。

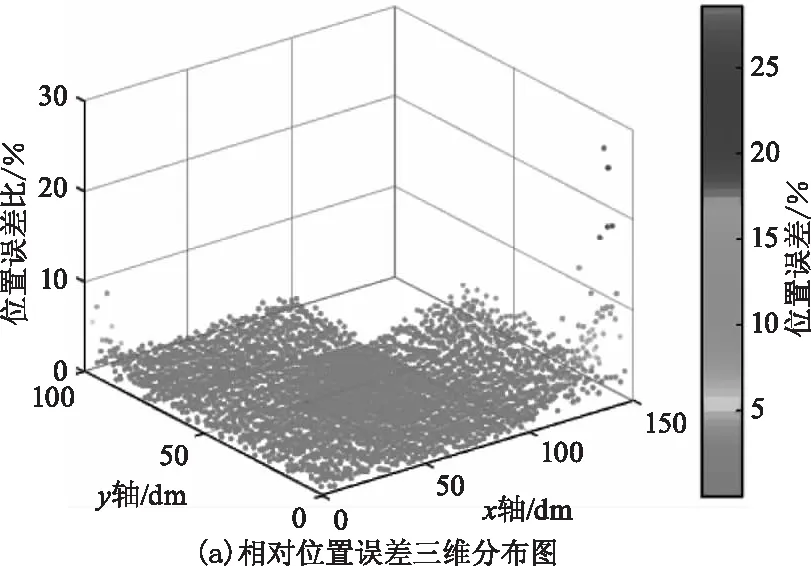
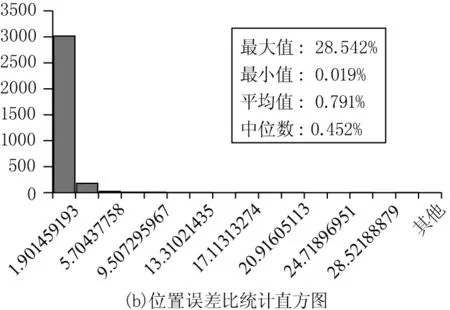
图6 位置定位误差

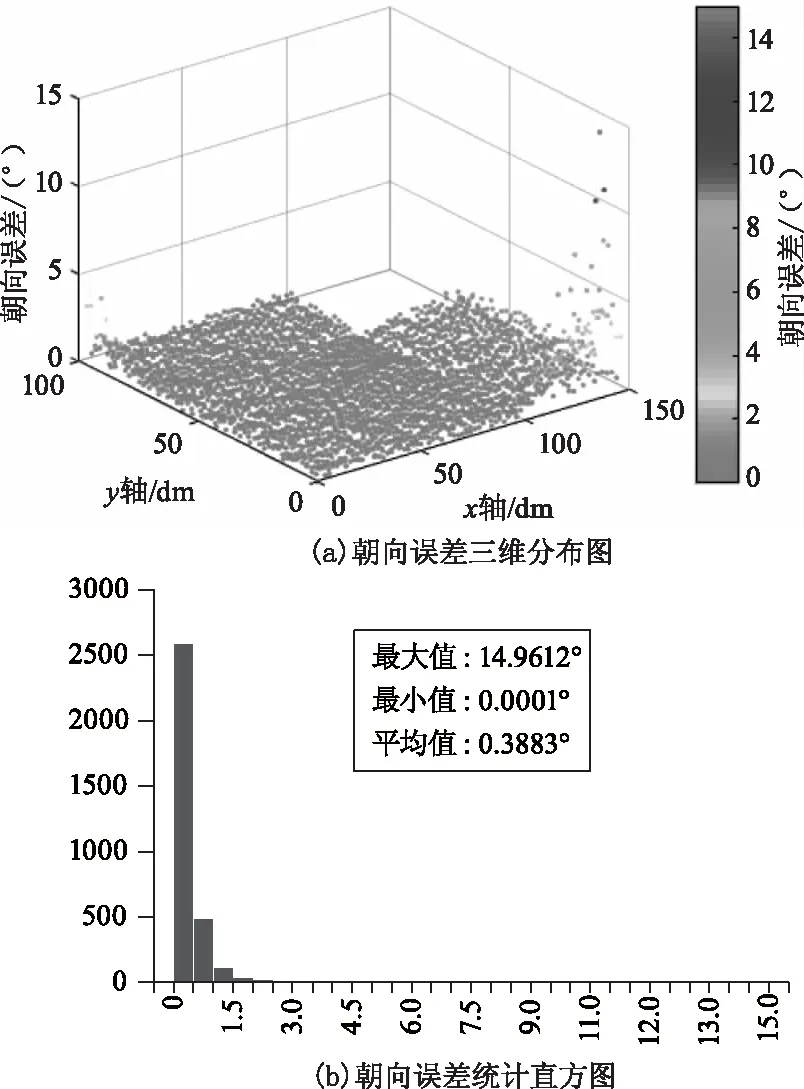
图7 朝向定位误差

综上,雷达在凸多边形地图内或非凸多边形地图内的无漏扫区域时,该算法的准确性最高,而在非凸多边形地图内的漏扫区域时算法精度有所下降。

7 结束语

本文提出了一种基于激光雷达的有界区域快速全局定位算法,为机器人在室内使用激光雷达传感器完成自身全局定位的需求提供了新思路和有效的算法方案。利用非凸多边形可由多个凸多边形叠加组合的原则对图形进行切分,并提取已知有界地图的特征向量,将全局定位问题转化为地图边界在车辆坐标系与地面坐标系上的特征向量匹配问题,实现了对激光雷达的精确全局定位。最终通过实验验证了该算法的有效性和准确性,发现该定位算法平均位置误差比为0.791 %,平均朝向误差为0.3883°。