变形L1正则化的高光谱图像稀疏解混

李 璠,吴朝明,张绍泉,胡 蕾,邓承志

(1.南昌工程学院 江西省水信息协同感知与智能处理重点实验室,江西 南昌330099； 2.江西师范大学计算机信息工程学院,江西 南昌330022)

1 引 言

高光谱遥感具有光谱分辨率高、图谱合一和光谱波段数目多等特点,已成为地质制图、植被调查、海洋遥感、环境监测等领域的重要技术[1]。然而,受成像光谱仪空间分辨率的限制和自然界地物复杂多样的影响,混合像元普遍存在于高光谱遥感图像中,其极大地限制了高光谱图像的应用范围[2]。混合像元分解是解决混合像元问题有效的方法,是保证高光谱遥感技术向定量化发展的前提[3]。

随着端元光谱库的普及以及稀疏表示理论[4]的迅速发展,Iordache等用已知端元光谱库替代从图像中选取端元集合,将稀疏约束引入到混合像元分解中,提出了稀疏解混的理论与方法[5]。稀疏解混不需要假设图像中有纯端元存在,同时不需要估计图像中包含的端元数目,是当前解混的研究热点[6]。稀疏解混的基本模型是一个非凸的组合优化问题,通常采用非平滑项“L0范数”表示。近年来,针对“L0范数最小化问题”提出了近似求解方法,最常见的是用L1范数代替L0范数[5]。对于L1稀疏正则化问题,变量分裂与增广拉格朗日方法(Sparse unmixing by variable splitting and augmented lagrangian,SUnSAL)[7]被证实是有效的求解方法,可以得到较满意的结果。然而,由于光谱库中的端元数量与通常参与混合像元的组分数量之间的不平衡,导致L1正则化解混的稀疏性和稳健性并不好。为了更好地表征稀疏度,目前已涌现出一些方法,如吴泽彬等[8]采用迭代加权L1正则化方法、Sun等[9]采用L1/2稀疏正则化方法、Deng等[10]采用平滑L0稀疏正则化方法、Chen等[11]采用Lp稀疏正则化等。这些方法虽然改善了稀疏性,但当p<1时,Lp范数函数不是Lipschitz连续的,因此对于较小的p值存在数值求解问题。针对该问题,有学者提出利用指数函数、对数函数或sigmoid函数等Lipschitz连续函数逼近L0范数[12-13]。

TransformedL1(TL1)正则化函数[14]是一个由绝对值函数组成的双线性变换的单参数族,与Lp(p∈(0,1])范数类似,通过控制参数a∈(0,∞)可任意表征L0和L1之间的范数,并满足无偏、稀疏和Lipschitz连续的性质。鉴于TL1正则化函数具有的这些优势,本文利用TL1正则化函数建立稀疏解混模型,并提出凸函数差分(Difference of Convex,DC)算法求解,即DCATL1算法。DCATL1算法收敛于满足一阶最优条件的驻点,对端元光谱库矩阵是否满足有限等距条件(Restricted Isometry Property,RIP)不敏感。

2 稀疏解混模型

线性混合模型假设在任何给定的光谱波段中,每个像元光谱是该像元中所有端元光谱的线性组合[2]。假设具有l个光谱波段,线性混合模型可描述成如下形式:

y=Mx+n

(1)

其中,y∈Rl×1表示某个像元的测量光谱；M∈Rl×q表示端元矩阵,q为端元数；x=[x1,x2,…,xq]T表示丰度向量；n∈Rl×1表示系统噪声。

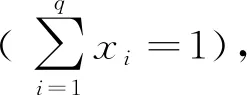
Iordache等[5]提出用已建立的地物光谱库取代端元矩阵,以避免图像中纯净像元不存在时无法提取完备的端元光谱。用已知的端元光谱库A代替端元集合M,线性混合模型转化为:

y=Ax+n

(2)

其中,A∈Rl×m是包含m条光谱曲线的端元光谱库;x∈Rm×1为对应A中各端元的丰度向量。

光谱库A中的端元光谱数m远远大于式(1)中的实际端元个数q,经稀疏分解获取的丰度向量x也是稀疏的,即x中非零值的个数q≪m,由此得到L0优化问题:

(3)

其中,第一项为重构误差项,第二项为稀疏性约束项；λ是平衡保真项和正则项之间权重的参数；‖x‖0表示x的L0范数,用L0范数来统计x中非零元素的个数；x≥0和1Tx=1分别表示ANC和ASC。由于该问题是典型的非凸优化NP难问题,求解困难。2006年,Tao和Candès[14]合作证明了在满足有限等距条件时,L0范数问题等价于L1范数凸优化问题:

(4)

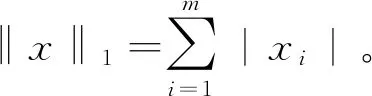
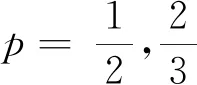
因此,本文提出了一种比L1范数更稀疏且易于求解、对端元光谱库是否满足有限等距条件不敏感的函数作为丰度稀疏约束项。

3 TL1正则化稀疏解混模型

TL1正则化函数ρa(x)[15]的定义:

(5)

ρa(x)是一个由绝对值函数组成的双线性变换的单参数族,具有无偏性、稀疏性和连续性[16-17]。随着参数a的变化,ρa(x)可以准确表征L0和L1之间的任意范数,近似Lp(p∈(0,1])范数。

从图1中可看出,a的值越大,曲线越接近|x|,a的值越小,曲线越趋于坐标轴。从图2中可看出,当a→∞,p=1时,ρa(x)和xp近似,逼近L1范数；当a→0,p→0时,ρa(x)和xp均趋于指示函数,逼近L0范数；在0≤x≤1范围内,ρa(x),a∈(0,∞)和xp,p∈(0,1]可以相互近似。

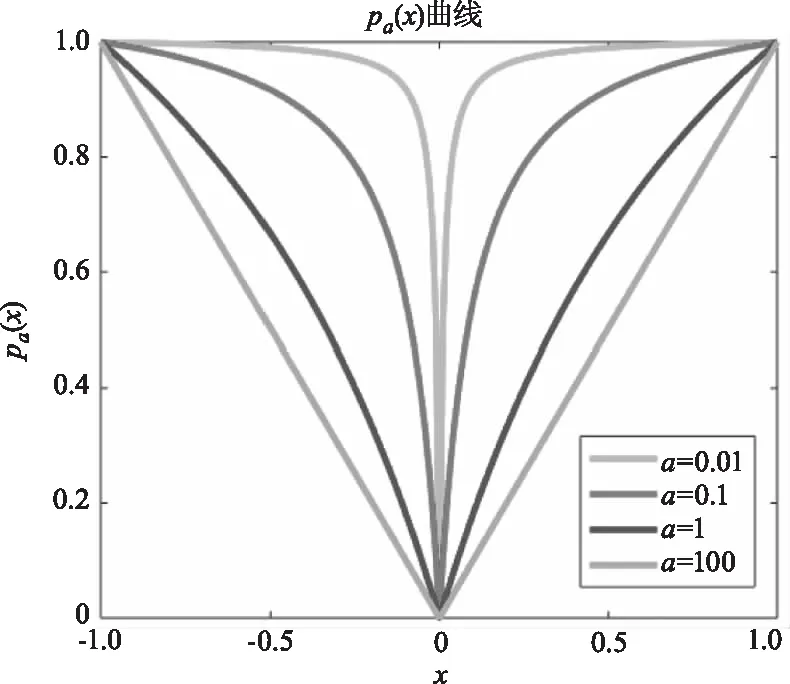
图1 参数a=0.01,a=0.1,a=1,a=100时,ρa(x)的曲线

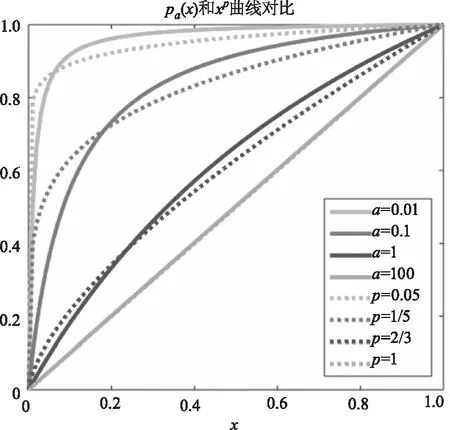
图2 参数a和p取不同值时,ρa(x)与xp曲线对比

将TL1的定义扩展到向量空间,向量x=(x1,x2,…xN)T∈RN,定义:

(6)

通过调整参数a,用TL1代替L0范数来解决高光谱稀疏解混问题,得到TL1正则项最小化模型:

(7)

4 TL1正则化解混数值求解

本文采用凸函数差分(DC)算法求解TL1正则化稀疏解混变分问题,即DCATL1算法。DCATL1求解算法包括外层和内层循环迭代,外层循环采用DC算法,将非凸的TL1正则化函数表示为两个凸函数之差,每步迭代求解一个强凸的L1正则化子问题,内层循环采用交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)[7]求解L1最小化问题。

将TL1正则化函数ρa(·)表示为两个凸函数之差:

(8)

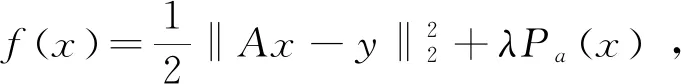
(9)

(10)

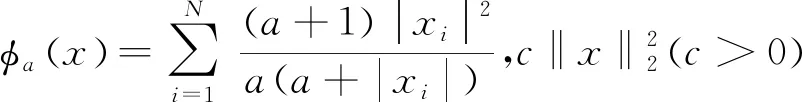
在迭代点xn,用函数h(x)近似表示其仿射函数hn(x)[19]:

hn(x)=h(xn)+〈x-xn,vn〉,vn∈∂h(xn)

∂h(xn)=λ∇φa(xn)+2cxn

次微分∂h(x)在x∈dom(h)是闭凸集,可做如下等价变换[19]:

inf{g(x)-hn(x):x∈RN}⟺inf{g(x)-〈x,vn〉:x∈RN}

定义上式的最优解为xn+1,则每步迭代解决以下强凸的L1正则化子问题:

(11)

使用ADMM方法求解式(11),引入变量z,并定义增广拉格朗日函数:

(12)

其中,uT是拉格朗日乘子;δ>0是罚参数。

对目标函数L(x,z,u)求偏导,分别得到x,z,u的最优解表达式:

xk+1=B-1W

(13)

(14)

uk+1=uk+δ(xk+1-zk+1)

(15)

其中,B=ATA+2cI+δI,W=ATy+vn+δzk-uk。

shrink(·,·)是软阈值算子,定义如下:

shrink(x,r)i=sgn(xi)max{|xi|-r,0}

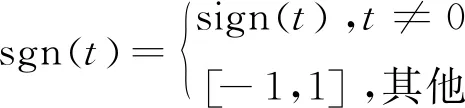
考虑ANC和ASC条件,最优化问题转换为:

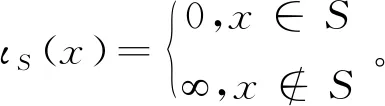
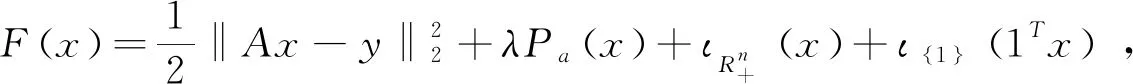
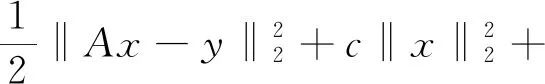
(16)

相应地,求最优解xn+1的子问题转换为:

(17)

使用ADMM方法求解式(17),可得:

xk+1=B-1W-C(1TB-1W-1)

xk+1=max(xk+1,0)

其中,C=B-11(1TB-11)-1。

综上所述,TL1正则化稀疏解混模型在ANC和ASC约束下的DC求解算法DCATL1如下:

5 实验与分析

5.1 模拟数据实验

模拟实验端元光谱库A由USGS光谱库splib06(包括498条光谱,每条光谱224个波段)中任意选择240条光谱曲线构成,即A∈R224×240,光谱范围0.4～2.5 μm。每个模拟高光谱图像由100个混合像元构成。丰度系数矩阵随机生成,且满足Dirichlet分布。生成3组高光谱模拟数据SD1、SD2、SD3,端元数k分别为2、4、6。在高斯白噪声污染的情况下进行实验,信噪比分别为30 dB、40 dB、50 dB。

采用信号重建误差比(Signal-to-Reconstruction Error,SRE),进行定量分析,其定义如下:

(18)

明算法的解混精度越高。同时,采用稀疏度(sparsity)[20]评价各解混算法丰度系数的稀疏性。稀疏度越小,表明得到的解越稀疏,解混效果越好。

表1给出不同信噪比和端元数情况下,SUnSAL和DCATL1算法获得的SRE(dB)和sparsity值(均为100次平均值),以及相应的正则化参数取值。可以看出DCATL1算法在所有情况下都获得了比SUnSAL算法高的SRE(dB)值,表明DCATL1算法的解混精度优于SUnSAL。在端元数量较少时(k=2),DCATL1的性能优势更加明显。同时,与SUnSAL算法相比,DCATL1算法获得更稀疏的结果,表明TL1正则化模型能够增强解的稀疏性。

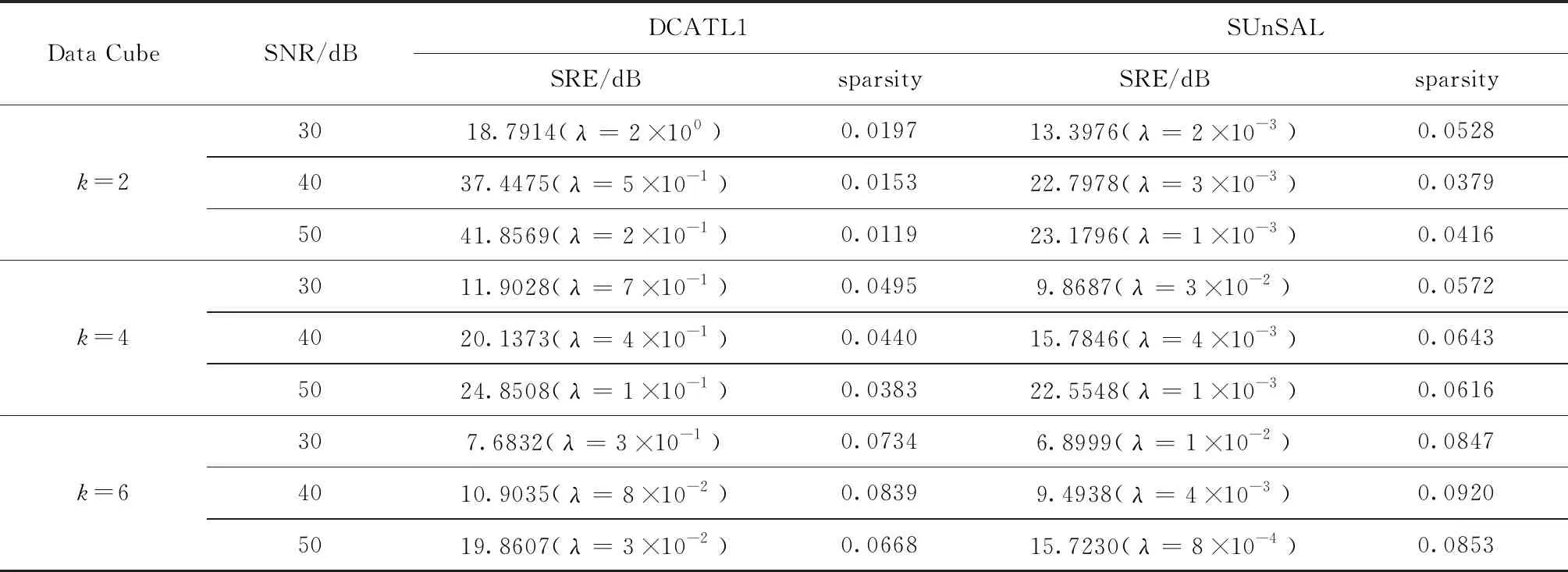
表1 各解混算法得到的SRE(dB)(a=100)和sparsity值

为进一步说明DCATL1的性能,图3给出在信噪比为30 dB的模拟数据集SD1上,两种解混算法的估计丰度图及真实丰度图。从图中可以看出,DCATL1估计出的丰度图比SUnSAL更接近于真实的丰度。SUnSAL估计出的丰度图中存在较多干扰丰度或者噪声,而DCATL1消除了大部分干扰,体现了TL1正则化模型比L1模型具有更好的稀疏性和更高的解混精度。

在稀疏解混算法中正则化参数λ可以平衡解的精确性和稀疏性。为分析参数λ对DCATL1算法的影响,图4绘制了信噪比分别为30 dB、40 dB和50 dB的情况下,端元数分别为2、4和6时,SRE(dB)值随参数λ的变化曲线。从图4中可以看出,随着信噪比的增大,λ最优取值越小,随着端元数减少,λ最优取值越大。在这几种不同的情况下,λ最优取值趋势基本类似,且参数的可选范围较大。

5.2 真实数据实验

为了验证DCATL1算法在真实高光谱图像场景下的有效性,采用美国内达华州的AVIRIS Cuprite(赤铜矿)遥感图像数据进行实验。选取250×191的像元子集,包括224个光谱波段,波长范围0.4～2.5 μm。去除1～2、105～115、150～170和223～224等低信噪比和水蒸气的吸收波段,剩下188个光谱波段数。图5显示了1995年通过USGS拍摄得到的矿物图,利用Tricorder 3.3软件[21]产品反映Cuprite矿区数据中各矿物的分布情况。在实验中,图5显示的矿物图作为各算法定性分析的参考,用它来判断各算法是否将该数据中的矿物分解出来了。

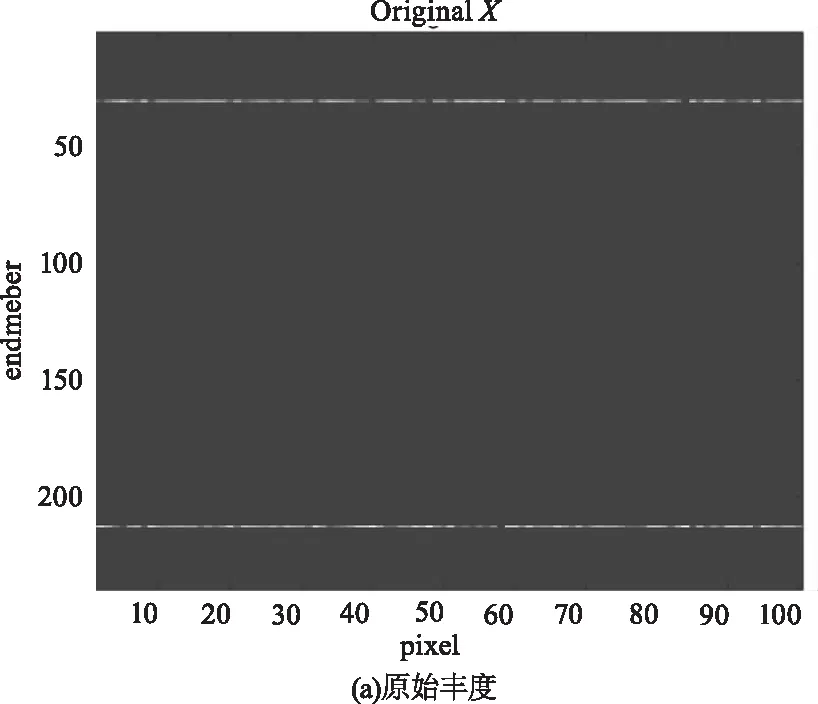
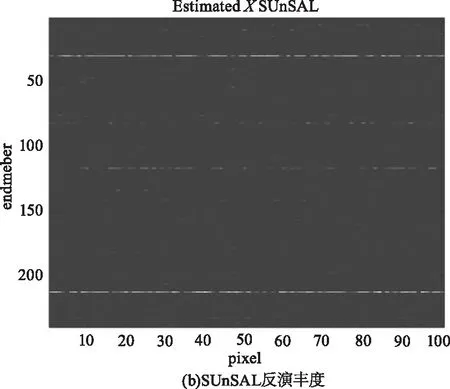
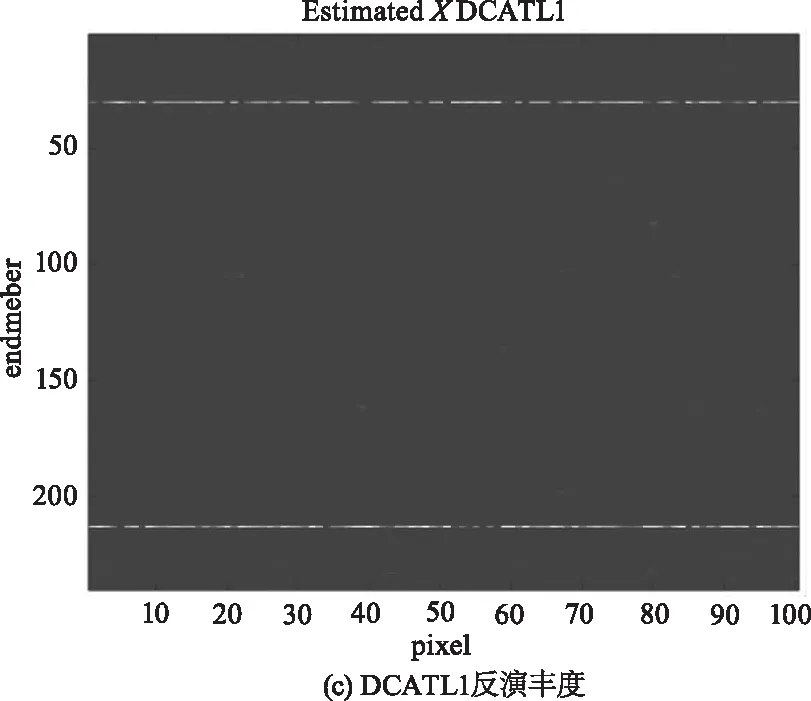
图3 SNR=30 dB时,模拟数据 SD1的反演丰度与原始丰度对比

实验利用SUnSAL和DCATL1算法分别对该Cuprite高光谱数据进行混合像元分解,估计出各端元的丰度图像并进行展示。选择Alunite(明矾石)、Buddingtonite(水铵长石)和Chalcedony(玉髓)三种矿物的Tricorder 分类图作为定性分析的参考,分析两种算法的性能。实验中,SUnSAL和DCATL1算法的正则化参数经验性地分别设置为λ=0.001,λ=0.2。

如图6所示,两种算法分解出来的效果与Tricorder分类图都较相似,表明了稀疏解混算法的有效性。

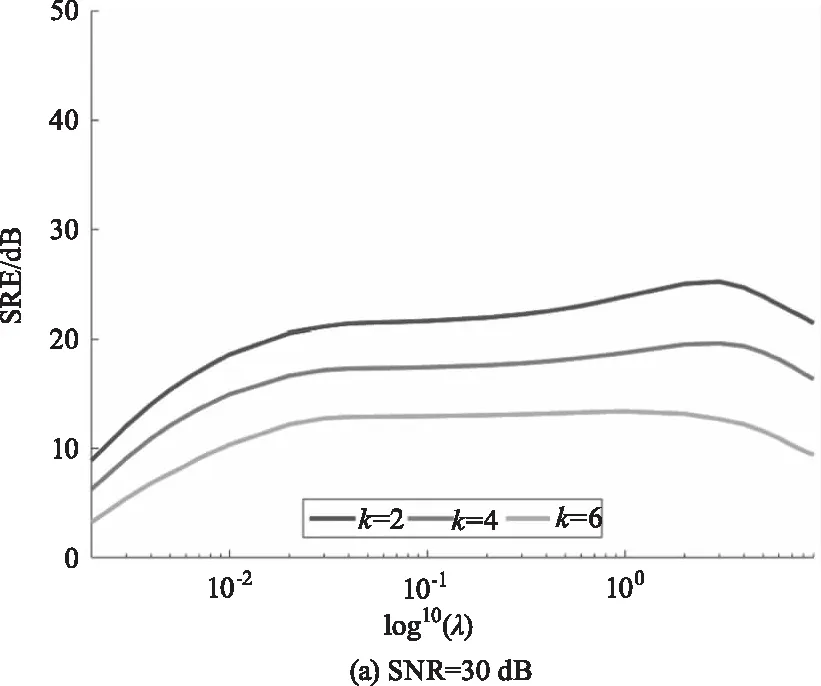
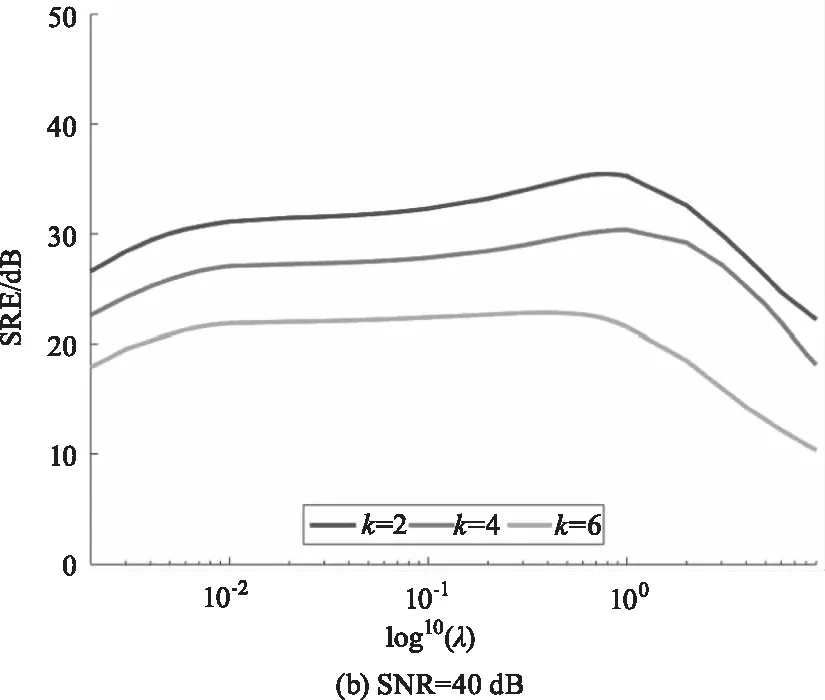
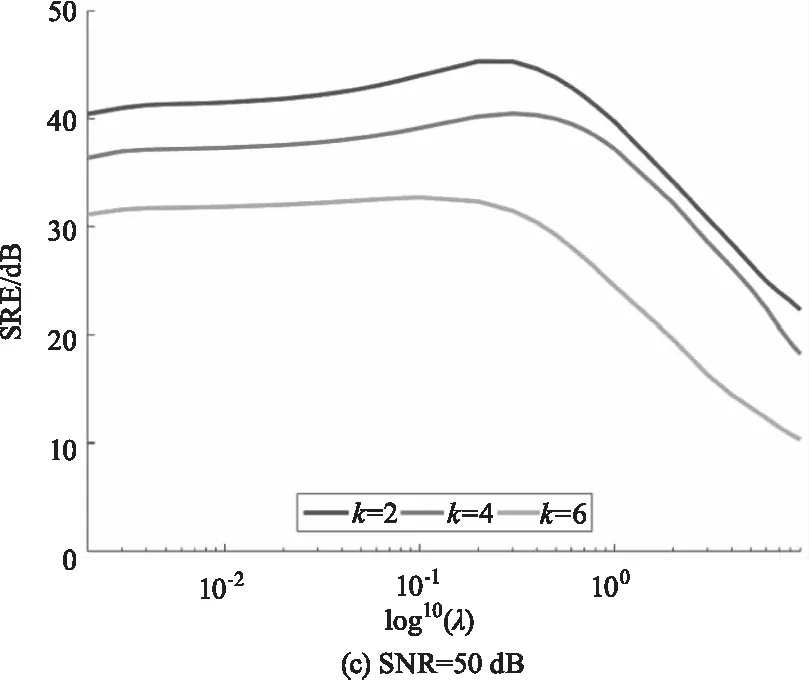
图4 不同信噪比和端元数情况下,DCATL1算法

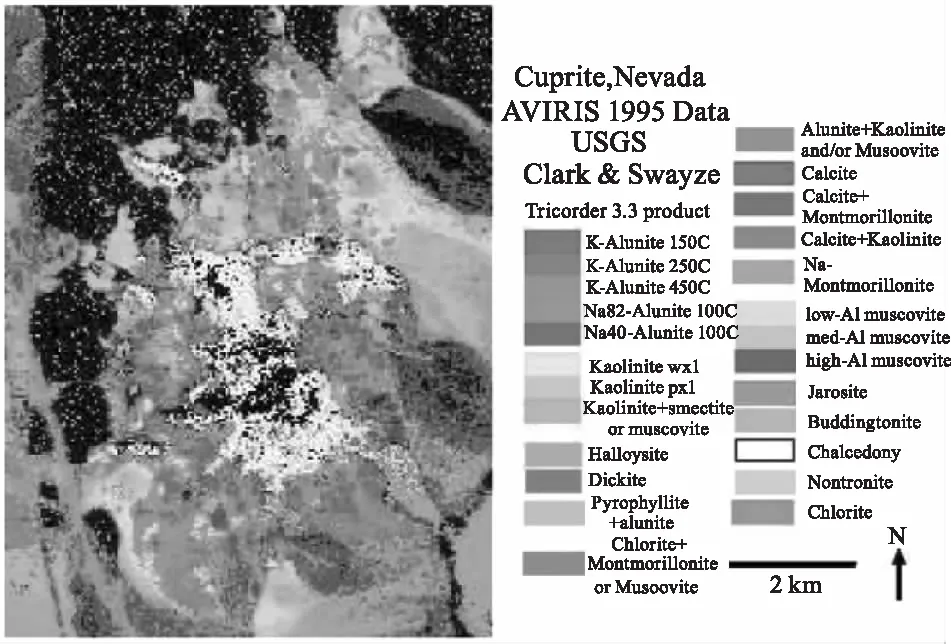
图5 USGS获得的内华达州赤铜矿区不同矿物所在的位置

然而,从图6中可以看出,DCATL1算法估计的丰度图(如Alunite明矾石)噪声较少,更接近于真实的参照图。此外,也计算了SUnSAL和DCATL1算法获得的稀疏度(sparsity),分别为0.0718和0.0459。从这些小的差异可以得出结论,本文提出的DCATL1算法使用了更少数量的像元来表达数据,具有更高的稀疏性。通过真实数据实验得到的结果表明,DCATL1算法能够提高解混精度。

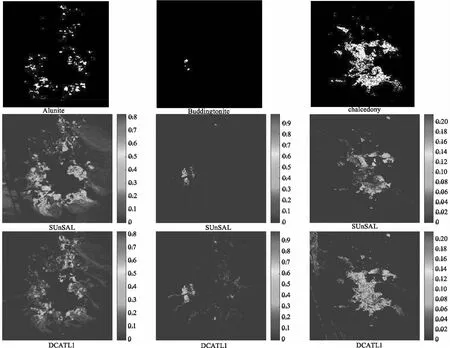
图6 在真实数据实验下SUnSAL和 DCATL1算法分别得到的矿物丰度图

6 结 论

本文提出TL1正则化的高光谱图像稀疏解混模型及其求解算法DCATL1,用稀疏、Lipschitz连续的TL1正则项代替稀疏回归模型中的L0范数,利用DC算法将非凸的TL1正则项函数分解为两个凸函数之差,再运用ADMM算法解决凸的子问题。TL1正则化模型比L1正则化模型具有更好的稀疏性和更高的解混精度。通过模拟和真实的高光谱数据集进行实验,验证了该方法的有效性和准确性。参数a依赖先验知识进行初始化。下一步将研究参数a的自适应选取,使目标函数由近似L1范数开始,当算法收敛到初始最优解时,通过迭代更新得到L0范数最小化的精确近似值,以提高算法自适应能力。