完美图形中的向量

江西南昌莲塘第二中学(330200) 唐水华

主题词 考点;平面几何图形;向量标化

平面向量的基本定理及在此基础上建立起来的平面向量的坐标表示是向量线性运算的根基,大多数同学都能很好地识记和理解平面向量的基本定理及基坐标表示.但在具体运用上往往就不尽人意.下面就有关平面几何图形与圆、圆锥曲线完美结合中的向量问题与大家分享一下,因为班门弄斧初创原题,不当之处在所难免,本来也是为了抛砖引玉!

【引例】 如图1 , 圆O是边长为的等边三角形ABC的内切圆,其与BC边相切于点D,点M为圆上任意一点,则2x+y的最大值为( )

图1

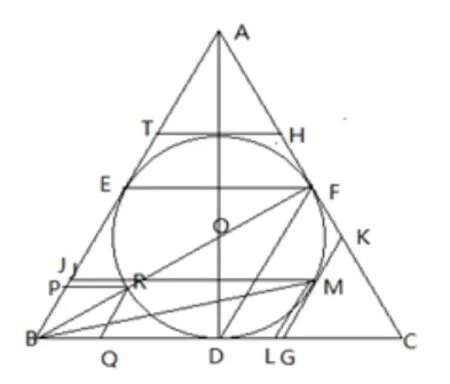
图2

【学生错解】

虽然上述解法似乎对平面向量基本定理的理解深刻,也对平面几何图形的知识掌握的蛮好, 但还是解答的不正确.事实上,当且仅当点M运动至AC中点F时,2x+y取得最大值2, 此题解错的原因在于x,y不能同时取得最大值

那么这个试题该如何才能较好地解析得更好,解答得条理清晰呢? 实际上,利用在平面向量基本定理基础上建立起来的平面向量坐标表示方法——坐标法,不妨为一种有效选择.

【分析】建立坐标系,写出相应的点坐标,得到2x+y的表达式,进而得到最大值.

【解析】以D点为原点,BC所在直线为x轴,AD所在直线为y轴,建立坐标系,如图3 所示.

因为圆O是边长为的等边三角形ABC的内切圆, 因此|AD|= 3, 因为因此|OD|=1, 即内切圆的半径为1, 以(0,1) 为圆心, 可得到点的坐标为:A(0,3),D(0,0),M(cosθ,1 + sinθ), 因此得到:即:因此最大值为2.故答案为: D.

图3

【评价】这个题目本质上是考查向量标化以及参数方程的应用,是以向量为载体求相关变量的取值范围,是向量与函数、不等式、三角函数等相结合的一类综合问题.通过向量的运算,将问题转化为解不等式或求函数值域,是解决这类问题的一般方法.

【例题1】如图4 所示,圆O是边长为的等边三角形ABC的外接圆,点M为圆弧AC上任意一点(含A、C两点),且的最大值为( )

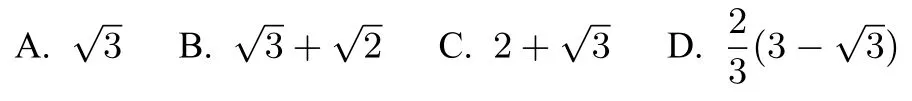
【分析】 从所给图像来看, 是标准的图形, 易于建立平面直角坐标系, 借助坐标法, 写出相应各点坐标而得到的表达式,进而可以求得其最值.

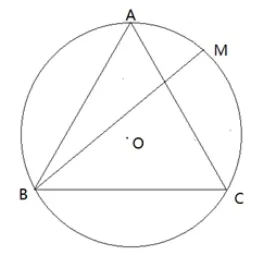
图4

图5

【解析】取BC中点D,以D点为原点,BC所在直线为x轴,AD所在直线为y轴,建立坐标系,如图5 所示.

因为圆O是边长为的等边三角形ABC的外接圆, 因此圆O的半径为2, 即可得到以(0,1) 为圆心, 半径为2 的圆方程为x2+ (y -1)2= 4, 根据上述坐标及借助圆的参数方程可得各点坐标为:且θ的范围为得 到:解得:x=(1 + 2 sinθ),y=所以的最大值为故答案为: C.

【评价】本题依然本质上是考查向量标化以及参数方程的应用,是以向量为载体求相关变量的取值范围,是向量与函数、不等式、三角函数等相结合的一类综合问题.通过向量的运算,将问题转化为解不等式或求函数值域,是解决这类问题的一般方法.

【例题2】如图6 所示的三角形ABC是腰长为等腰直角三角形,椭圆以BC为长轴,且经过腰AB和AC的中点E、F,M为椭圆上半部分曲线上任意一点(含B、C两点),且(x,y ∈R),则2x+y的最大值为( )

【分析】从所给图像来看,是标准的图形,易于建立平面直角坐标系,借助坐标法,写出相应各点坐标而得到2x+y的表达式,进而可以求得其最值.

图6

图7

【解析】取BC中点O,以O点为原点,BC所在直线为x轴,AO所在直线为y轴,建立坐标系,如图7 所示.因为三角形ABC是腰长为等腰直角三角形,椭圆以BC为长轴,且经过腰AB和AC的中点E、F,因此|BC|= 4,所以椭圆的方程为= 1, 显然a= 2,且AC中点F的坐标为(1,1) 在椭圆上, 可解得b2=所以椭圆方程确定为= 1, 此时可借助椭圆的参数方程,设 点M为M(2 cosθ,sinθ),A(0,2),B(-2,0),C(2,0).因为= (2 cosθ+2,= (4,0), 所以(2 cosθ+ 2,=(2x+4y,2x),解得:x=因此2x+y=因此2x+y的最大值为2.故答案为: D.

【评价】本题依然本质上是考查向量标化以及参数方程的应用,是以向量为载体求相关变量的取值范围,是向量与函数、不等式、三角函数等相结合的一类综合问题.通过向量的运算,将问题转化为解不等式或求函数值域,是解决这类问题的一般方法.

【小结】从以上几个试题的解答过程来看,平面向量的基本定理及建立在此基础上的向量坐标表示是解答的基础,充分借助图形及有关曲线的特征,建立平面直角坐标系,使求解数学表达式的最值或范围在向量标化的基础上转化为函数问题,通过与函数、不等式和三角函数等的结合可获得条理清晰的解答过程和正确的结论,这显然是解答此类问题的有效选择.因此从本质上来讲,当然这些都源于平面向量的基本定理及其坐标表示:

1.平面向量基本定理: 如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2.其中,不共线的向量e1,e2叫做表示这一平面内所有向量的一组基底.其实当且仅当a在e1,e2上分解的分向量与方向一致时,λ1,λ2取得正值,否则取负值,分解的分向量为零向量时,取值为0,即a与e1共线时,λ2= 0,即a与e2共线时,λ1=0.

2.平面向量的坐标表示: (1)在平面直角坐标系中,分别取与x轴,y轴方向相同的两个单位向量i,j 作为基底.对于平面内的一个向量a,有且只有一对实数x,y,使a=xi+yj,把有序数对(x,y)叫做向量a的坐标,记作a= (x,y),其中x叫做a在x轴上的坐标,y叫做a在y轴上的坐标.

认识、理解和掌握了上述平面向量的基本定理及其坐标表示,那么求解代数式的最值或范围问题通过向量问题坐标化转化为函数、不等式和三角函数的问题就不会显得神秘,正确求解就是必然事件.

【例题3】 如图8 所示, ΔABC是边长为3 的等边三角形, 圆O交的三边AB、BC、CA分别为P2,P3,P4,P5,P6,P1,且分别三等分三边,D是弧P1P2的等分点,E是弧P3P4的等分点,M是弧DE上任意一点(含D、E两点) ,(x,y ∈R),则2x+y的取值范围为( )

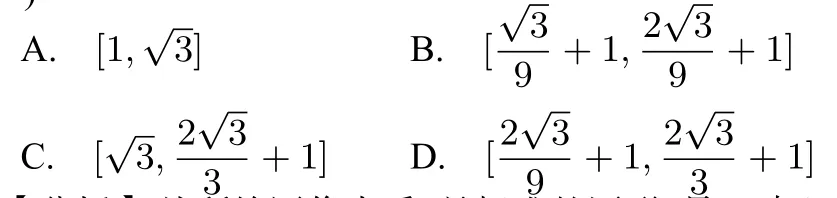
【分析】从所给图像来看,是标准的图形,易于建立平面直角坐标系,借助坐标法,写出相应各点坐标而得到2x+y的表达式,进而可以求得其取值范围.

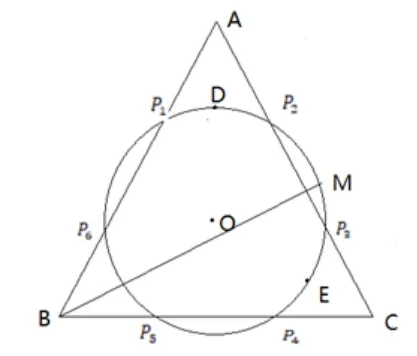
图8

图9

【解析】以O点为原点,过O且与AO垂直的直线为为x轴,AO所在直线为y轴,建立坐标系,如图9 所示.

由建立坐标系可知, 因为O为三角形ABC过点A的高的三等分点, 而P6,P2也是AB、AC的三等分点, 所以x轴必过P6,P2两点, 因为|AC|= 3, 因此|AP3|= 2, 因此|OP3|= 1, 因此圆O的半径为1,因此圆方程为x2+y2= 1, 根据上述坐标及借助圆的参数方程可得各点坐标为:M(cosθ,sinθ),A(0,得到:解得:因为M从E点沿弧运动到点D,因此θ的范围为因此因此2x+y的范围为故答案为: B.

【例题4】如图10 所示的三角形ABC是腰长为等腰直角三角形,抛物线以A为顶点,开口向下且经过等腰直角三角形两腰AB和AC的中点E、F,D为BC的中点,M为抛物线的曲线E -→A-→F上任意一点(含E、F两点),且则x+y的取值范围为( )

【分析】从所给图像来看,是标准的图形,易于建立平面直角坐标系,借助坐标法,写出相应各点坐标而得到x+y的表达式,进而可以求得其取值范围.

图10

图11

【解析】 取BC中点D, 以点A为原点O, 过A且与AD垂直的直线为为x轴,AD所在直线为y轴,建立坐标系,如图11 所示.

因为三角形ABC是腰长为等腰直角三角形, 因此|BC|= 4, 且抛物线经过腰AB和AC的中点E、F,因此E(-1,-1),F(1,-1), 因此设抛物线方程x2=-2py,把F点坐标代入方程, 可得抛物线方程为x2=-y, 因此可设点M为(m,-m2), 且m ∈[-1,1];D(0,-2), 因此=(m,-m2+2)==x(2,2)+y(4,0)=(2x+4y,2x).解得:x=因此x+y=因此故答案为: A.

总的来说,通过原理性知识分析,让学生去发现平面向量基本定理及其坐标表示是有关向量线性运算转化的依据,虽然此类问题具有一定的综合性,有理由相信,通过本文的学习,学生的数学抽象、逻辑推理、数学运算和直观想象等数学核心素养应当会得到提升.