2020年广东省中考数学第22题解法评析与拓展研究

广东省中山市第一中学(528400) 宋海培

2020年的广东省中考已落下帷幕,各市的评卷工作也已完成.笔者参与了广东省中考数学第22 题(圆的综合题)的评卷工作,目睹了同学们五花八门的解答.经过评卷后的统计,本题平均分仅为2.8 分(满分8 分),平均得分率为0.35,可见同学们的回答并不理想.这道题可以怎样解? 这道题相关的图形结构还有哪些可以总结的性质? 其他省市的数学中考对这些性质是否有过考查? 我们在教学中该怎么做? 这引起了我的很多思考,现整理出来,供大家参考.

1 原题呈现

如图1,在四边形ABCD中,AD//BC,∠DAB= 90°,AB是⊙O的直径,CO平分∠BCD.

(1)求证: 直线CD与⊙O相切;

(2)如图2,记(1)中的切点为E,P为优弧上一点,AD=1,BC=2,求tan ∠APE的值.

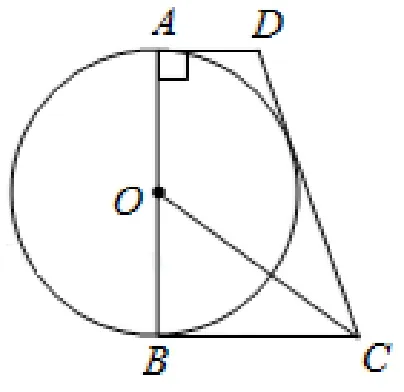
图1

图2

2 解法评析

(1)证明: 如图3,过点O作OE⊥CD于点E.

∵AD//BC, ∠DAB=90°, ∴∠OBC= 180° -∠DAB= 90°, 即OB⊥BC.∵CO平分∠BCD,OE⊥CD,OB⊥BC, ∴OB=OE.∵AB是⊙O的直径,∴OB是⊙O的半径, ∴OE也是⊙O的半径.∴直线CD与⊙O相切.

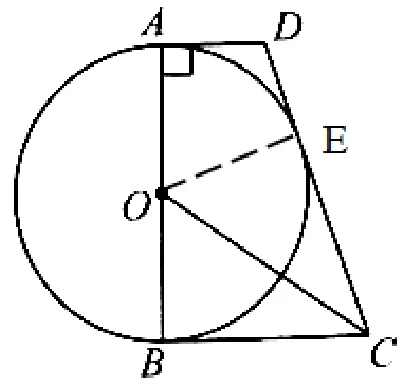
图3

解法评析(1): ①,切线的判定通常认为有两种常见题型及对应方法:本题的切线证明属于“无交点: 作垂直,证半径”这一类型,即⊙O与直线CD的公共点尚未明晰,所以可以采取先作垂线段OE,再证明这条垂线段的长度等于圆的半径,从而证明直线CD是⊙O的切线;

②,利用角平分线性质证明线段相等,也可通过全等来证明;

③,说明垂线段OE等于半径;

④,直线CD经过半径外端且垂直于半径,是圆的切线.

以上是本题的常规解法, 在评卷过程中发现了个别学生的其他解法, 同样达到了证明切线的目的.如采用下面的思路: 在CD上截取CE=CB, 用SAS 证得ΔBCO∽= ΔECO, 进一步可同样得到OE⊥CD以及OB=OE,所以直线CD与⊙O相切.

(2)解: 如图4,连接OD,∵直线CD、AD、CB与⊙O相切, ∴AD=DE= 1,BC=CE= 2, ∠ADO= ∠EDO,∠BCO=∠ECO,∴∠AOD=∠EOD,CD= 3.∠AOD.∵AD//BC,∴∠ADE+∠BCE=180°,∴∠ODE+∠OCE= 90°, ∴∠DOC= 90°.∵OE⊥CD, ∠ODE=∠CDO,∴ΔODE∽ΔCDO,∴OD=∴在RtΔAOD中,OA=∴tan ∠AOD=

图4

解法评析(2): ⑤,因为∠APE的三角函数不容易直接求得,进行角度的转换是关键一步.此处的方法是结合圆周角定理和切线长定理将∠APE转移至∠AOD,也可以转移到其他角,如∠ABE.这决定了接下来的具体求解路径,不同的解法亦可由此而发端.

⑥,运用切线长定理和相似等知识求得相关数据.此部分的具体求解方法也较多,相关的图形性质很丰富,在后面详细论述.

⑦,运用三角函数的定义和等量代换求得答案.

以上是第(2)题的一种解法(解法1),若将∠APE转换为∠ABE,在ΔABE中进行求解也可,具体如下.

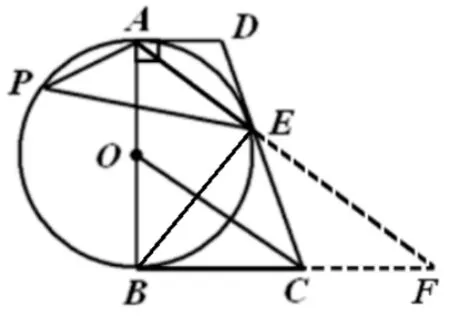
图5

解法2: 如图5, 连接BE, 延 长AE交BC延 长线于点F, 由得∠APE=∠ABE,∵AD//BC,∴∠DAE= ∠CFE, 易 得ΔADE∽ ΔFCE,AD=DE= 1,CE=BC= 2,根据射影定理有BE2=AE · EF, ∴tan ∠APE= tan ∠ABE=

解法2 不需具体求出半径长,只需挖掘出AE与BE的关系即可,显得更简捷.这当然需要解题者有不断总结反思从而形成的敏锐的解题感觉.解法2 在挖掘AE与BE的关系时用到射影定理这一基本图形的相关知识.实际上,在前面的解法1 中,同样可以运用射影定理获得另外的解题路径.

解法3: 如图4,在RtΔCOD中由OE2=ED·EC求得OE=即OA=以下略.

本题还有其他解法, 如解法4: 作DH⊥BC, 得BH=AD= 1 =CH, 由勾股定理求得DH==AB, 故OA=(以下略).这是典型的梯形辅助线解法,也是一种比较容易想到的解法.

3 拓展研究

从以上解法评析可以看到,本题的图形结构中蕴含了丰富的性质,值得进行研究和总结梳理,具体如下.

如图6,已知AB是⊙O的直径,AD和BC是⊙O的两条切线,DC与⊙O相切于点E,连接BE、OC相交于点F,连接OD、AE相交于点H.图中蕴含的丰富性质包括但不限于以下(证明不难,此处略):

图6

(1)全等三角形有: ΔAOD∽= ΔEOD,ΔBOC∽= ΔEOC,ΔBCF∽= ΔECF,ΔADH∽= ΔEDH,ΔAOH∽= ΔEOH∽= ΔOEF∽= ΔOBF;

(2)相等的线段有:AD=DE,BC=EC,FB=FE=OH,AH=EH=OF,AO=EO=BO=r等;

(3) 具有2 倍关系的线段有:BE= 2OH(中位线) ,AE=2OF(中位线),AB=2OE(斜边上中线)等;

(4) 角平分线有:OD平分∠ADC,OD平分∠AOE,OC平分∠BCD,OC平分∠BOE;

(5) 相等的角有: ①∠DAE= ∠AOD= ∠EOD=∠DEA=∠OEB=∠OCE=∠OCB=∠OBE,

②∠ODA= ∠ODE= ∠OAE= ∠OEA=∠COE=∠BOC=∠CEB=∠CBE,

③∠COD=∠AEB=∠AHO=∠BFO=90°等;

(6) 相似三角形有: ΔDAH∽ΔAOH∽ΔDOA∽ΔOCB∽ΔBCF∽ΔOBF∽ΔDCO∽ΔABE等;

(7)平行关系有:CO//AE,DO//BE,AD//BC等;

(8) 垂直关系有:OA ⊥ AD,OB ⊥ BC,OD ⊥AE,OC ⊥BE,OE ⊥CD,AE ⊥BE等;

(9)特殊四边形有: 四边形OFEH是矩形;

(10)重要线段关系还有:AD+BC=CD,AD·BC=OA2=OE2=ED·EC=r2,DO·BE=CO·AE=2r2.

4 他山之玉

当我们对以上图形结构以及蕴含的图形关系有深入的了解后,2020年广东省中考数学第22 题以及许多类似的题目解决起来思路就可以开阔得多,达到“左右逢源”、“条条大路通罗马”的境界.下面我们一起来欣赏其他省市对以上图形结构的考查,这里只简要列举几例.

1.(2018 大庆中考)如图7,∠B= ∠C= 90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( ).

A.30°B.35°C.45°D.60°

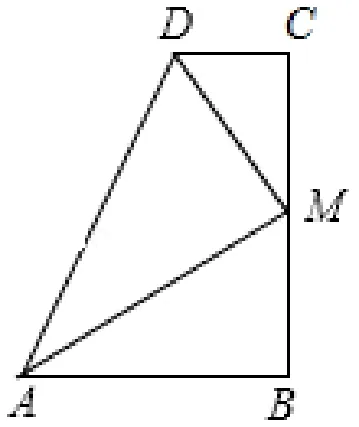
图7

图8

【分析】先根据平行线的性质求出∠DAB.如图8,作MN⊥AD于N,结合角平分线的性质和判定求得∠MAB.

【简评】若剔除圆的背景,2020年广东省中考数学第22题实际上蕴含本题的结构.

2.(2019 武汉中考)已知AB是⊙O的直径,AM和BN是⊙O的两条切线,DC与⊙O相切于点E, 分别交AM、BN于D、C两点.

(1)如图9,求证:AB2=4AD·BC;

(2)如图10,连接OE并延长交AM于点F,连接CF.若∠ADE=2∠OFC,DA=1,求图中阴影部分的面积.

图9

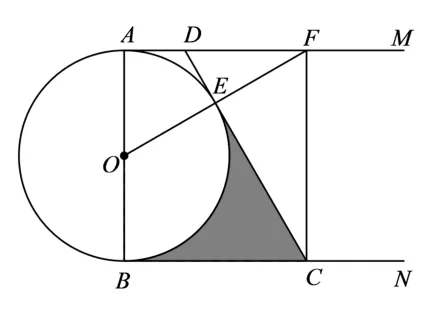
图10

【分析】(1)如图11,连接OD,OC,OE.∵AM,BN,CD是⊙O的切线,∴OA⊥AD,OB⊥BC,OE⊥CD,AD=DE,BC=EC, ∠ODE=∴AD//BC, ∠ODE+ ∠OCE=(∠ADC+∠BCD) =90°.∵∠ODE+ ∠DOE= 90°, ∴∠OCE= ∠DOE.又∵∠OED= ∠CEO= 90°, ∴ΔODE∽ΔCOE.OE2=ED · EC, ∴4OE2= 4ED · EC, ∴AB2=4AD·BC.

图11

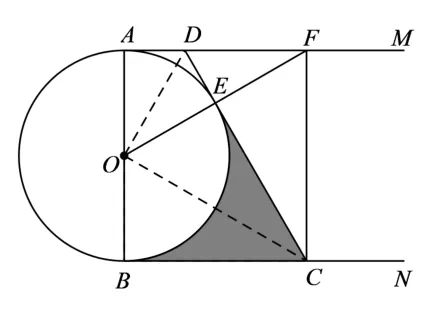
图12

(2)解: 如图12,由(1)知∠ADE=∠BOE,∵∠ADE=2∠OFC,∠BOE= 2∠COF,∴∠OFC= ∠COF,∴ΔCOF是等腰三角形.∵OE⊥CD,∴CD垂直平分OF.∴∠AOD=∠DOE= ∠OFD= 30°, ∠BOE= 120°.∴r=OA=BC=OB ·tan 60°= 3.∴阴影部分的面积S=

【简评】本题较充分地展示了前面总结的图形性质的运用.

3.(2016 鄂州中考) 如图13 所示,AB是⊙O的直径,AM和BN是⊙O的两条切线,DC与⊙O相切于点E,连接OD、OC、BE、AE,BE与OC相交于点P,AE与OD相交于点Q,已知AD=4,BC=9.以下结论:

①⊙O的半径为②DO//BE, ③PB=④tan ∠CEP=

其中正确的结论有( )

A.1 个 B.2 个 C.3 个 D.4 个

图13

图14

【分析】 ①如图14,过点D作DF⊥BC于点F,∵AM和BN是⊙O的两条切线, ∴AB⊥AD,AB⊥BC, ∴四边形ABFD是矩形, ∴AD=FB,AB=FD, 又∵AD= 4,BC=9,∴FC=9-4=5,∵AM,BN,CD是⊙O的切线,∴AD=DE,BC=EC,∴DC= 9+4 = 13,在RtΔDFC中,DC2=DF2+FC2, ∴DF== 12,∴AB=FD=12,∴⊙O的半径是6.故①错误;

②如图15, 连接OE,∵AD,ED是⊙O的切线,∴AD=DE, ∠OAD=∠DEO= 90°, 又∵OD=OD,∴ΔAOD∽= ΔEOD,∴∠AOD= ∠EOD=∴∠AOD= ∠ABE,∴DO//BE.故②正确;

图15

③根据勾股定理得,OC=由①知OB= 6, 易知ΔOPB∽ΔOBC, 则∴PB=故③正确;

④易知∠CEP ＞∠ECP, 所以CP ＞ EP, 故tan ∠CEP ＞1,故tan ∠CEP=错误.

综上,正确的答案为: B.

【简评】本题充分展示了本文所探讨的这个典型图形的性质.熟练使用前面总结出的方法和结论,不难快速解出此题.

5 教学启示

最近八年(2013年到2020年),广东省中考数学试卷的几何综合题都是用圆的综合题来把关考查学生的推理素养.这些圆的综合题虽然千变万化,但是善于总结基本图形、具有较高推理素养的学生就能很好地解决.

基本图形具有典型性和生长性.教材中的基本概念、基本方法、基本原理对应的图形还有一些典型的例题与习题都是基本图形(典型图形)的重要来源.如本文重点分析的2020年广东省中考数学第22 题第(1)小题实际上与人教版九上教材第98 页中的例1 大同小异(类型相同,方法相通,形式有异).另外人教版九上教材第102 页习题中的第11 题,第125 页复习题中的第15 题均有与本题高度相似的图形结构.如果平时做好相关的训练以及注意解题后的总结,这道广东省的中考题是不难攻克的.

引导学生分析和总结基本图形(典型图形)是提高推理素养的重要途径.我们在教学中应该加强引导学生对基本图形的研究和整理归纳,在分析和总结基本图形的过程中不断落实基础知识、夯实基本技能,积累基本活动经验、感悟数学基本思想,从而切实提高分析问题、解决问题的能力,提高推理素养.