基于一致性理论的多旋翼飞行器编队控制方法

黎海青，苗昊春，张健松，张一杰

(1.西安现代控制技术研究所，陕西 西安 710065；2.华中科技大学 人工智能与自动化学院，湖北 武汉 430074)

近年来，四旋翼飞行器因其体积小、可垂直起降和机动灵活等优点受到了广泛关注。与单架飞行器相比，多架飞行器组成编队协同执行任务能提高工作效率并提高系统容错率，可以完成更复杂的任务，在通信中继、搜救及侦察等方面有着广泛的应用[1-3]。

在多架飞行器协同工作时，机群需要组成合适的队形。一方面，飞行器之间需要保持适当的间距以避免发生碰撞和离群等情况，另一方面，许多特定的任务，如通讯中继、搜索救援等，需要飞行器组成特定的队形。目前，已有许多飞行器编队方法，如领导者-跟随者方法[4]、行为策略方法[5]和虚拟结构方法[6]等。文献[7]研究了针对智能体的编队控制，提出一种基于虚拟结构的分布式编队控制算法，并对该算法的稳定性进行了理论分析。文献[8]针对多无人机系统建立虚拟刚体模型,实现了实时的人机交互，并在虚拟刚体坐标系下研究了无人机的队形变换和避障问题[9]。这些方法既有其自身的优势，但也存在一些不足。领导者-跟随者方法易于实现，但没有跟随者的信息反馈。因此，整个编队的自主性不足，而且领导者的故障将可能导致整个编队的失控。行为策略方法是一种基于仿生学的方法，其优点是可以分布式实现，并可以扩展到很大的集群，缺点则在于编队的稳定性无法保证，并且很难分析编队的特征。虚拟结构方法物理意义明确，具有良好的鲁棒性，但该方法需要大量的计算能力和较宽的通讯带宽，难以在工程中应用。

一致性理论已被大量用于地面无人车和多卫星系统在固定拓扑、时变拓扑以及通信延时等情况下的编队控制。文献[10-12]提出了一种基于一致性编队控制方法，其基本思想是每个个体根据其相邻个体的状态更新其自身状态，最终使所有个体的状态收敛到共同的值。但是，上述文献都将智能体描述成一阶模型，系统较为简单。

针对以上研究存在的对象模型过于简单和稳定性不足等问题，将四旋翼飞行器描述为二阶系统，拟提出基于二阶一致性算法的多旋翼飞行器编队控制方法。基于一致性的编队策略，通过图论的方法构建了飞行器编队的通讯拓扑结构，并利用有向图表示集群中个体和个体之间的作用关系，设计了一种分布式编队控制器。其中，位置控制器用于实现期望编队轨迹的跟踪并保持指定的编队队形，姿态控制器用于稳定每架飞行器的姿态。最后，通过仿真验证了所设计的编队控制方法的有效性和优越性。

1 基于图论的编队结构描述

考虑N架同构的飞行器组成编队，在编队飞行中，每架飞行器除了完成自身的闭环控制外，还需与其他飞行器保持指定的距离。为了便于描述编队中个体之间的通讯关系，用有向图描述飞行器编队的通讯拓扑结构。

将编队中所有飞行器用一组节点集合V={v1,v2,…,vN}表示，节点vi表示飞行器i。飞行器j对飞行器i的影响，用有向图中的一条边(vi,vj)表示，编队中所有的影响关系用一组边集合E⊆{(vi,vj∶vi,vj∈V)}描述。令π={1,2,…,N}表示飞行器编号，各架飞行器之间的影响强度由加权矩阵W=[wij]∈RNN表示，若(vi,vj)∈E，则wij>0，表示飞行器j对飞行器i存在通讯关系。而当飞行器j对飞行器i无通讯关系时，则wij=0。此外,对于任意i∈∏，wii=0。使用有向图G=(V,E,W)描述飞行器编队的通讯拓扑结构。在有向图G中，如果存在一个边的子集，且可连接有向图中所有节点，那么称该图包含一个有向生成树。由文献[13]可知，在时不变固定通信拓扑条件下，当且仅当通信拓扑结构存在一簇有向生成树时，飞行器编队可达到渐近一致。

2 旋翼飞行器模型

考虑所研究的飞行器是同构的，以其中一架飞行器i为例，建立其平移和旋转动力学模型。

在四旋翼无人飞行器的模型当中，假设定义α={Eαx,Eαy,Eαz}表示地球惯性的坐标系，β={Eβx,Eβy,Eβz}表示原点在四旋翼质心上的载体坐标系，四旋翼飞行器模型如图1所示。

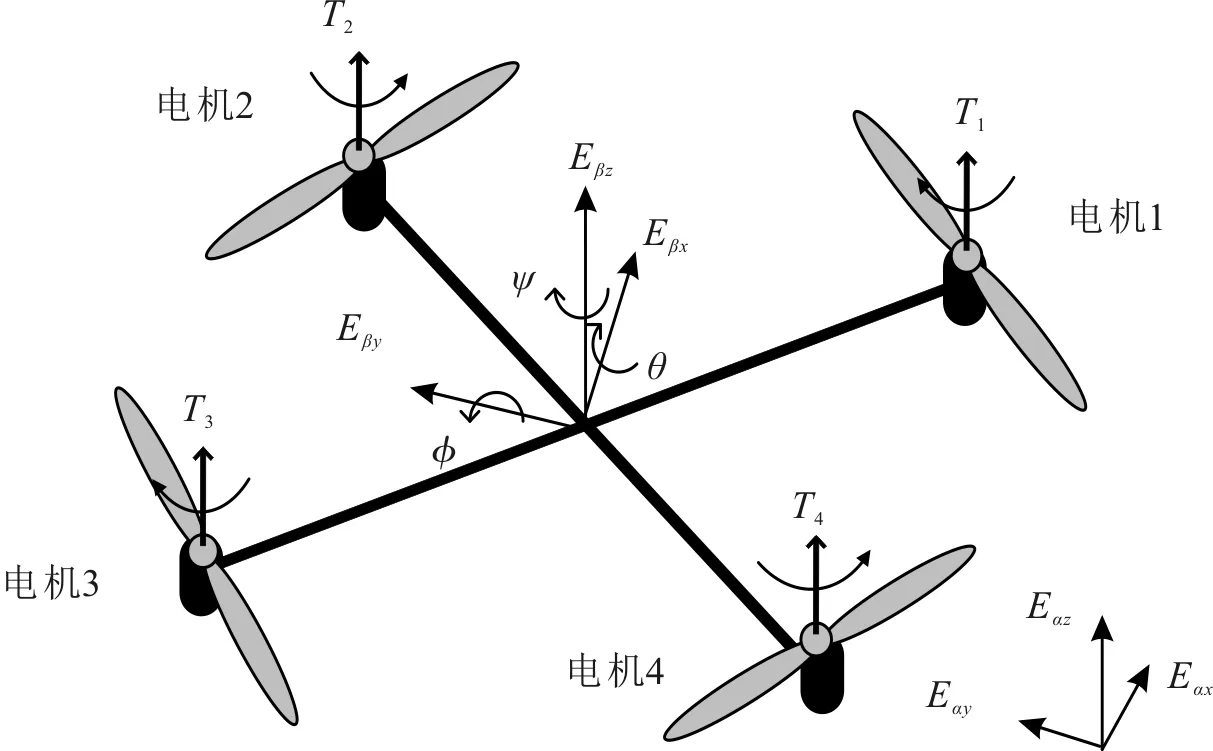
图1 四旋翼飞行器模型

令pi=[pxi,pyi,pzi]T∈R3×1和Θ=[φi,θi,ψi]T∈R3×1分别表示飞行器i的位置和姿态角。其中，φi、θi和ψi分别为滚转角、俯仰角和偏航角。Rbi表示坐标转换矩阵，其表达式为

那么，飞行器i的平移和旋转动力学模型的表达式分别为

(1)

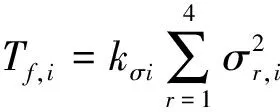
4个电机的控制输入指令的表达式分别为

由于飞行器i具有6个自由度即高度、横向和纵向位置以及3个姿态角和4个控制输入即uzi,uΘ1,i,uΘ2,i,uΘ3,i，其是一种多输入多输出的欠驱动系统。此外，可以看出，式(1)中描述的飞行器i的动力学模型是高度非线性和耦合的。

3 编队控制器设计

3.1 控制问题描述

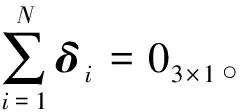
(2)

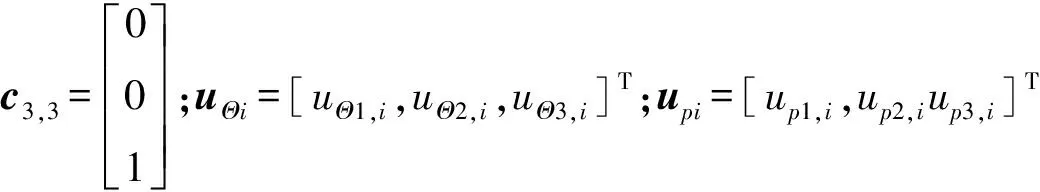
(3)

3.2 位置控制器设计

位置控制器用于实现期望编队轨迹的跟踪，并保持指定的编队队形。位置线性二次型调节器(Linear Quadratic Regulator，LQR)控制upi可以设计为

(4)

式中：N为飞行器个数；μP为耦合参数；对角矩阵Kp∈R3×3和Kv∈R3×3为位置LQR控制参数；αi是常数，取值范围为0～2，表示虚拟编队领导者和飞行器i之间的通讯权重，若αi>0，那么虚拟编队领导者可以向飞行器i发送信息，否则αi=0。定义KL=[Kp,Kv]为位置LQR控制参数矩阵，令

其中，PL是Riccati方程的正定解，则有

3.3 姿态控制器设计

姿态LQR控制器输出uΘi可以设计为

(5)

式中，KΘ,Kω∈R3×3是姿态LQR控制参数矩阵。KF=[KΘ,Kω]表示姿态LQR控制器参数。定义矩阵

式中，PF是Riccati方程的正定解，则有

通过基于图论构建的通信有向图和上述编队控制器设计方法可知，编队轨迹的参考信号由虚拟领导者提供，只有部分的飞行器个体可以获得参考信号。因此，整个位置控制器是分布式的和时不变的，意味着飞行器i的控制器设计仅取决于自身及其邻居的位置和速度信息。

基于小增益理论[15]可以证明，整个闭环控制系统是渐进稳定的。

4 数字仿真

在数字仿真中，3架四旋翼的模型参数选择为mi=2 kg,lbi=0.5,kσi=2.0,kτi=0.96,gi=9.81 m/s2及Ji=diag{0.1,0.1,0.06}kg·m2(i=1,2,3)，参数矩阵Bpi和BΘi的表达式分别为Bpi=diag(1,1,)和BΘi=diag{10.0,10.0,16.0}。

有向图G=(V,E,W)用于描述3架四旋翼编队的通讯拓扑结构。其中：V={v1,v2,v3},E={(v1,v2),(v2,v3)}，W=[wij]。w12=0.8,w23=0.7，若(vi,vj)∉E，那么wij=0。只有第1架四旋翼可以从虚拟编队领导者获得信息。因此，α1=1.5,α2=0，α3=0，α4=0。四旋翼编队的通讯拓扑结构及编队队形如图2所示。

图2 四旋翼编队的通讯拓扑结构及编队队形

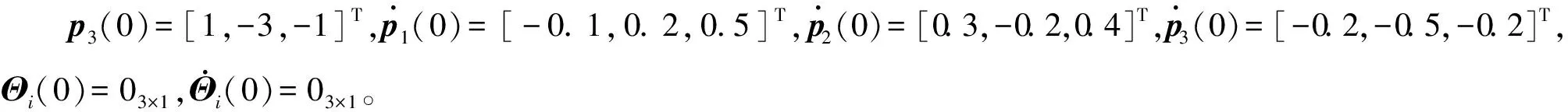
需要跟踪的虚拟编队领导者的期望轨迹为pr(t)=[3t,3t,4t]T，并且3个四旋翼需要保持一个恒定的三角形队形，3个四旋翼之间的距离分别为δ1=[1,1,0]T,δ2=[-1,1,0]T，δ3=[-1,-1,0]T。此外，每架四旋翼的偏航角需要稳定在0°。

位置和姿态的LQR控制参数选择分别表示为QL=diag{8,8,8,1,1,1},ΓL=I3,ΓR=I3,QR=1 000×diag{2.3,2.3,2.3,1,1,1}，μp=3.5。

四旋翼编队三维轨迹、X-Z视图、X-Y视图、位置跟踪误差、编队速度曲线、编队姿态曲线、位置控制器输出、姿态控制器输出如图3至图10所示。其中：图3至图5为四旋翼编队位置轨迹图，所采用的编队控方法可以实现期望的编队轨迹参考信号的跟踪，全程保持指定的三角编队队形；图6至图7为位置跟踪误差及速度曲线，四旋翼编队位置跟踪速度较快，在2 s左右达到收敛，稳态误差小于0.2 m；图8为编队姿态曲线，在俯仰角和滚转角在2 s左右收敛，偏航角稳定保持在0°，跟踪效果较好；图9至图10为位置控制器和姿态控制器输出曲线，可见控制器输出满足要求。

图3 四旋翼编队三维轨迹

图4 四旋翼编队X-Z视图

图5 四旋翼编队X-Y视图

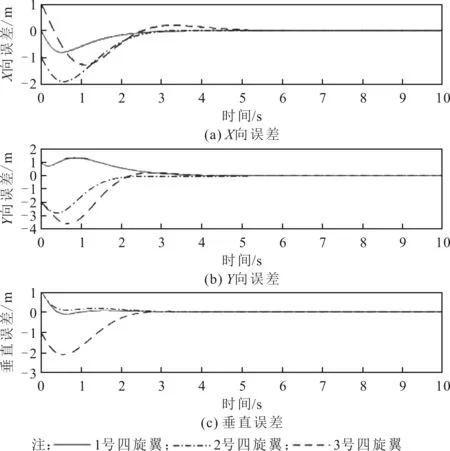
图6 四旋翼编队位置跟踪误差

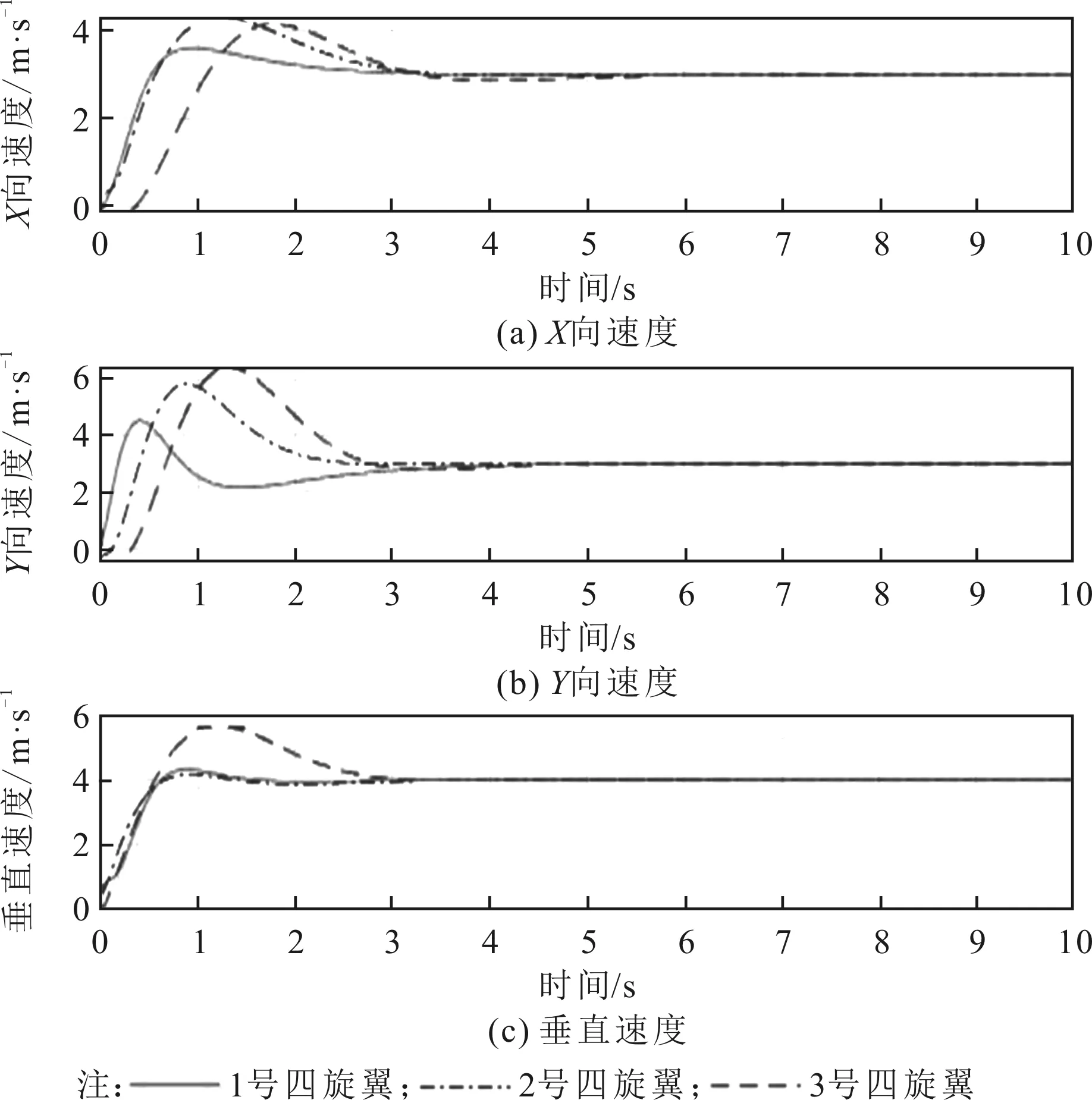
图7 四旋翼编队速度曲线

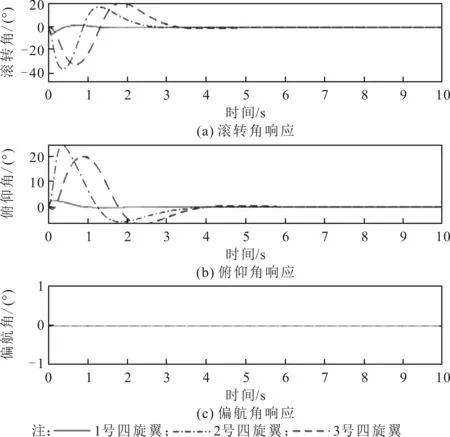
图8 四旋翼编队姿态曲线

图9 四旋翼位置控制器输出

图10 四旋翼姿态控制器输出

5 结语

针对多架飞行器的编队控制问题，提出一种基于一致性理论的编队控制算方法。利用图论方法对整个系统进行了建模，构建了飞行器编队的通讯拓扑结构，并以3架飞行器为例，设计了由位置LQR控制器和姿态LQR控制器组成的分布式控制器，实现了编队飞行轨迹跟踪与队形保持任务。仿真结果表明，该控制方法能够实现多架四旋翼飞行器的编队控制，清晰描述指定编队状态，飞行轨迹跟踪和队形保持精度较高，编队控制算法有效。