悬浮弹多旋翼悬浮装置翼间气动干扰特性分析

张宏乐，钱建平，郭 淳，苏文杰

(南京理工大学 机械工程学院， 南京 210014)

1 引言

悬浮弹是一种新型弹药，被用于保护海上舰船目标和重要军事工事而提出的一种新概念“被动式”低空防御武器。悬浮弹工作原理是由炮射母弹抛撒大量子弹，子弹依靠自身悬浮装置实现短暂悬浮或减速下降，从而在指定空域构建悬浮弹幕群，实现对来袭目标的拦截与毁伤[1-2]。本文悬浮子弹升力由多旋翼悬浮装置提供，因此悬浮子弹多旋翼间的气动干扰特性研究对于提高子弹的悬浮能力具有重要意义。

对于旋翼气动特性的研究，苏京昭等人通过对不同结构参数的旋翼模型进行研究，得到单旋翼的结构参数对其气动力的影响，为悬浮弹悬浮装置旋翼结构参数的选择提供了依据[1]。肖天航等人建立了低雷诺数非定常流场的数值方法，并将其应用于微型飞行器[3]。黄水林等人建立了对纵列式直升机双旋翼气动干扰特性分析的自由下洗流迭代方法，并对纵列式双旋翼气动干扰特性进行分析[4]。

悬浮弹采用多旋翼悬浮装置提供弹体所需升力，因此必然存在旋翼间的气动干扰，进而直接影响装置悬浮能力。本文利用多重坐标系和动网格模型对GWS6030×2型单旋翼流场进行CFD仿真计算，并与理论值进行对比，证明该仿真模型在旋翼气动力及流场计算的可靠性，并利用此CFD仿真方法研究旋翼间干扰对多旋翼气动力特性的影响。分析旋翼结构参数对翼间气动干扰的影响，从而为悬浮子弹的多旋翼悬浮装置设计提供参考。

2 单旋翼流场与气动特性CFD仿真

本文选取GWS6030×2型旋翼，通过建立多重参考坐标系(MRF)和动网格模型对旋翼旋转过程中的气动力特性进行仿真研究[5]。首先对旋翼进行几何建模，利用多重坐标系构建其旋转计算域和空气计算域(即固定域)。通过ICEM对空气计算域进行区块划分，对空气计算域与旋转域边界层网格和旋翼表面边界层网格进行局部网格加密，并检查Skewness等网格质量参数，保证网格质量和计算精度，最后对旋转域网格和固定域网格进行拼装。

本次仿真采用Realizablek-epsilon湍流模型，其适用于复杂几何的外部流动问题，自由流过程模拟结果比标准模型的结果好，且在低雷诺数时的近壁面处理更加精确，鲁棒性更高。选择流体为不可压缩，定义旋转域旋转坐标系和空气计算域固定坐标系，网格类型分别为动网格、静网格，并设置旋转坐标系转速(即旋翼转速)。为有效模拟自由流，将固定域壁面边界条件设为outflow、进出口边界为压力入口(pressure-inlet)和压力出口(pressure-outlet)，设置旋翼表面边界条件为无滑移的壁面(wall)，旋转域与固定域接触面边界为内表面(interface)[6]。

图1为旋翼流场在yOz平面速度矢量分布图，观察其流场分布，基本符合旋翼滑流理论中单旋翼流场的特性[7]。通过修正的动量叶素法对GWS6030×2型旋翼的拉力和阻力矩进行理论计算[8-9]，并与仿真结果进行对比来验证此CFD仿真法所得结果可靠性。

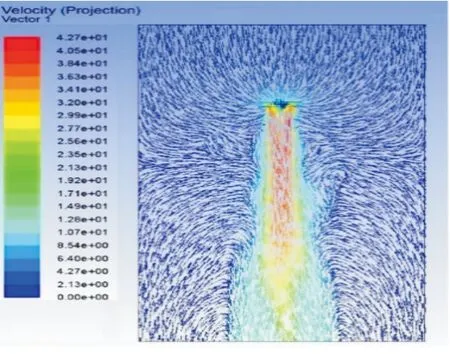
图1 转速n=13 000 r/min旋翼流场速度矢量分布图

悬浮弹拟重1 kg，对于多旋翼悬浮装置的单个旋翼至少提供拉力分别为5 N(二旋翼)和2.5 N(四旋翼)。因此对GWS6030×2型旋翼在转速为6 000～20 000 r/min区间内，进行拉力和阻力矩的仿真值与理论计算值进行对比。

图2和图3分别为GWS6030×2型旋翼拉力和阻力矩随转速变化的理论计算曲线与仿真值曲线。

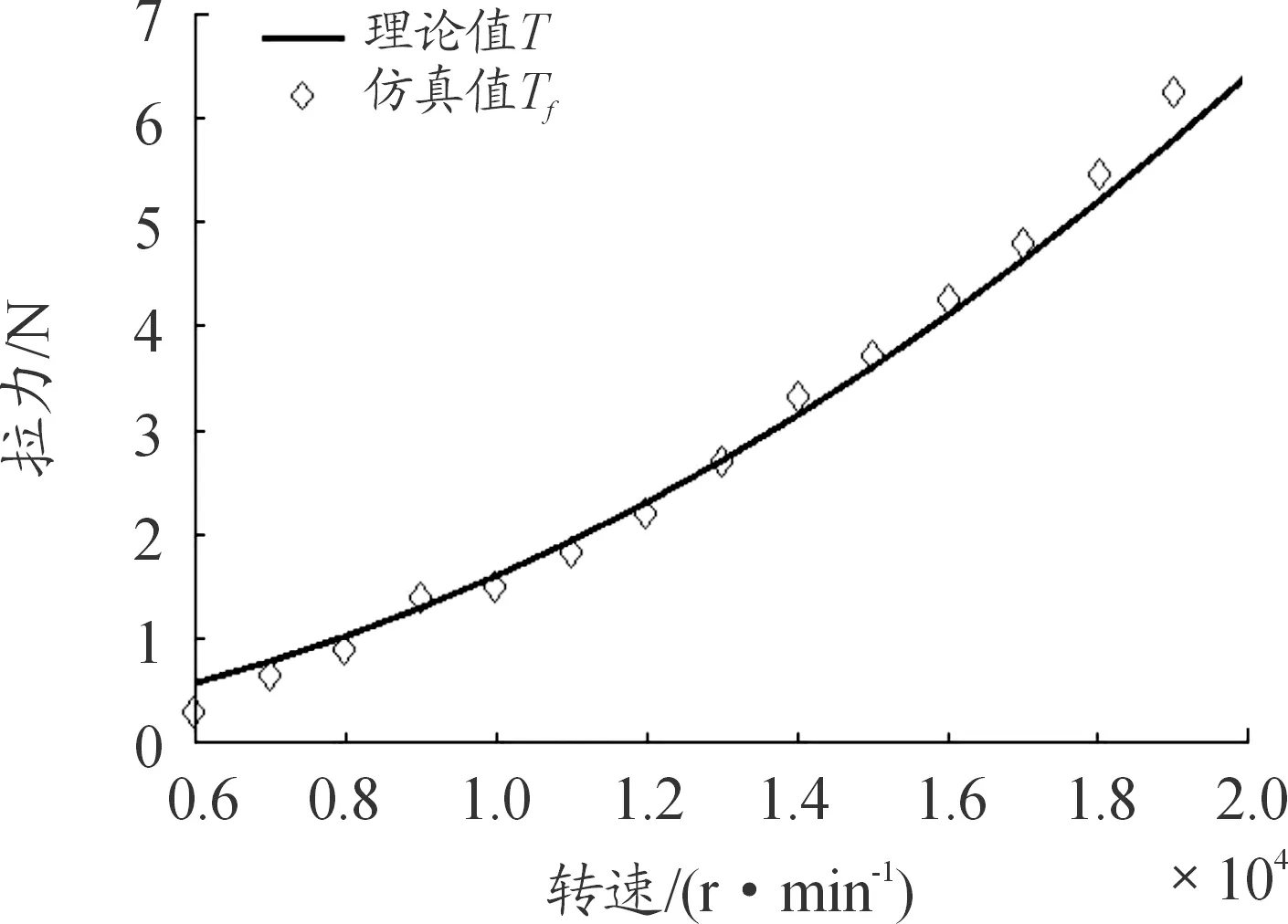
图2 GWS6030×2型旋翼拉力-转速曲线

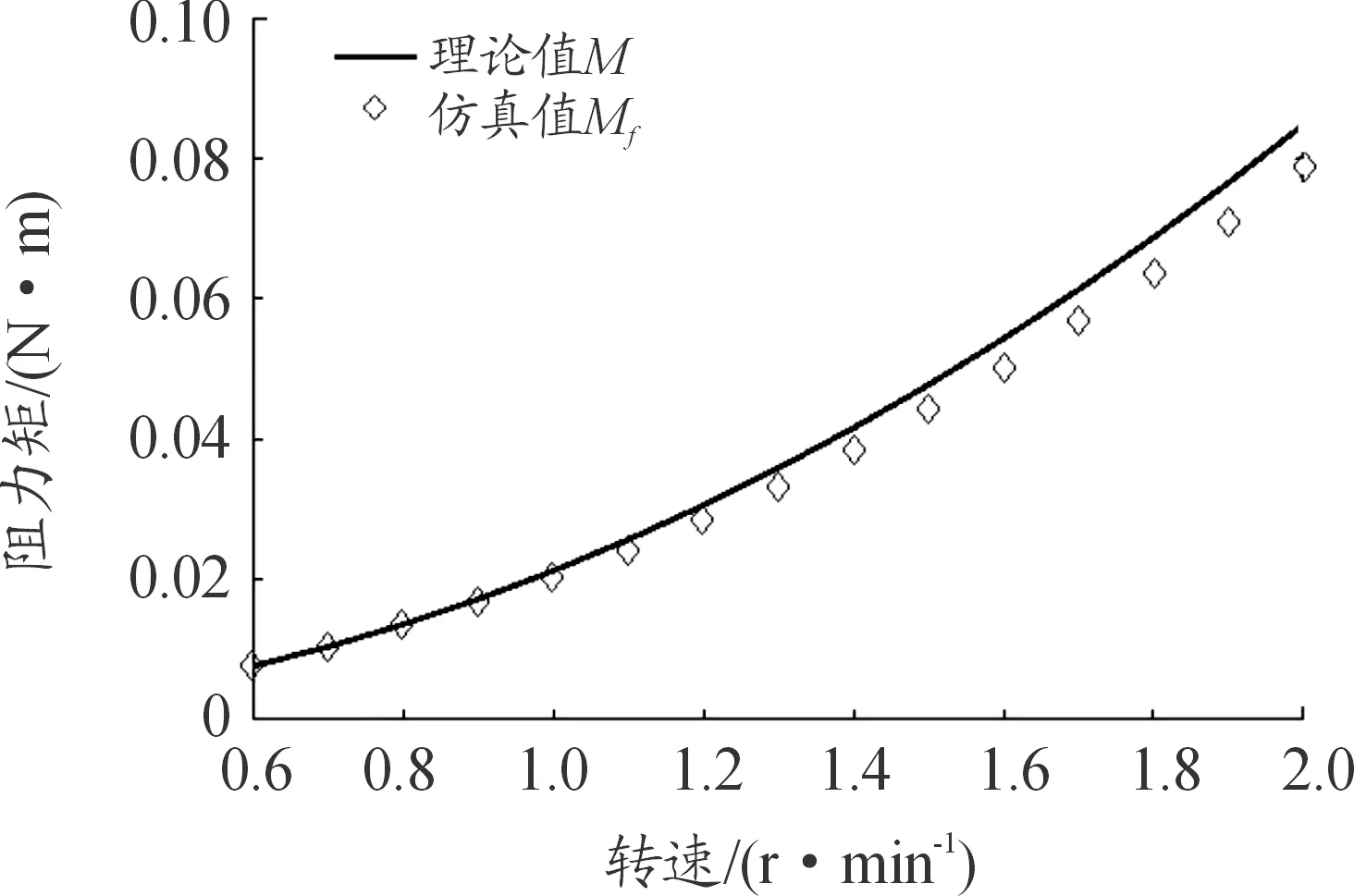
图3 GWS6030×2型旋翼阻力矩-转速曲线

观察图2和图3可知，本文采用的流体仿真方法所得结果与理论计算曲线基本相符拉力和阻力矩随转速变化趋势符合旋翼气动特性规律[10]。在理论计算时，采用矩形桨叶旋翼进行计算简化，而在仿真时用GWS6030×2型旋翼进行建模仿真。GWS6030×2型旋翼与矩形桨叶相比具有更好的气动性能翼型，因此随转速增加，旋翼拉力仿真值较理论值高且具有较低的阻力矩，符合旋翼结构参数的气动力影响规律[1]。

综上所述，本文采用的CFD方法对GWS6030×2型旋翼流场及气动力特性仿真准确性较高，可用于后文旋翼结构参数对翼间气动干扰特性的影响研究。

3 多旋翼气动干扰分析

旋翼流场的实质是耦合各干扰源及其下洗流的复杂流场，在该流场中旋翼产生下洗流的影响占主导地位，多个旋翼间下洗流将会产生干扰并导致复杂的干扰影响。因此旋翼间距将直接影响气动干扰程度，进而影响到整个悬浮装置的升力。本文利用前述CFD方法及GWS6030×2型旋翼模型，通过改变旋翼间距，求解不同间距下双旋翼及四旋翼所提供升力，并与单旋翼升力无干扰叠加的结果进行比较，来分析旋翼间距对升力的影响。

GWS6030×2型旋翼桨叶数为k=2，螺距H=76.2 mm，桨叶直径D=152.4 mm。由于三旋翼需额外平衡装置抵消反旋扭矩，从而较多占用悬浮子弹体积与重量，且三旋翼翼间气动干扰与二旋翼类似，故此处不予考虑。采用双旋翼和四旋翼2种分布方式，为抵消反旋扭矩相邻旋翼旋转方向相反、对角旋翼旋转方向相同。为提高普遍性，本文选取旋翼旋转半径R为基准，旋转区间距变化区间为0.1R～1.5R,即旋转轴间距L为2.1R～3.5R，次增量为0.1R进行仿真。

3.1 双旋翼气动干扰特性

对二旋翼进行几何建模如图4，图中圆柱区域为旋翼旋转计算域，L为旋翼间距。通过控制旋翼转速不变，改变旋翼间距L，对旋翼进行仿真计算。

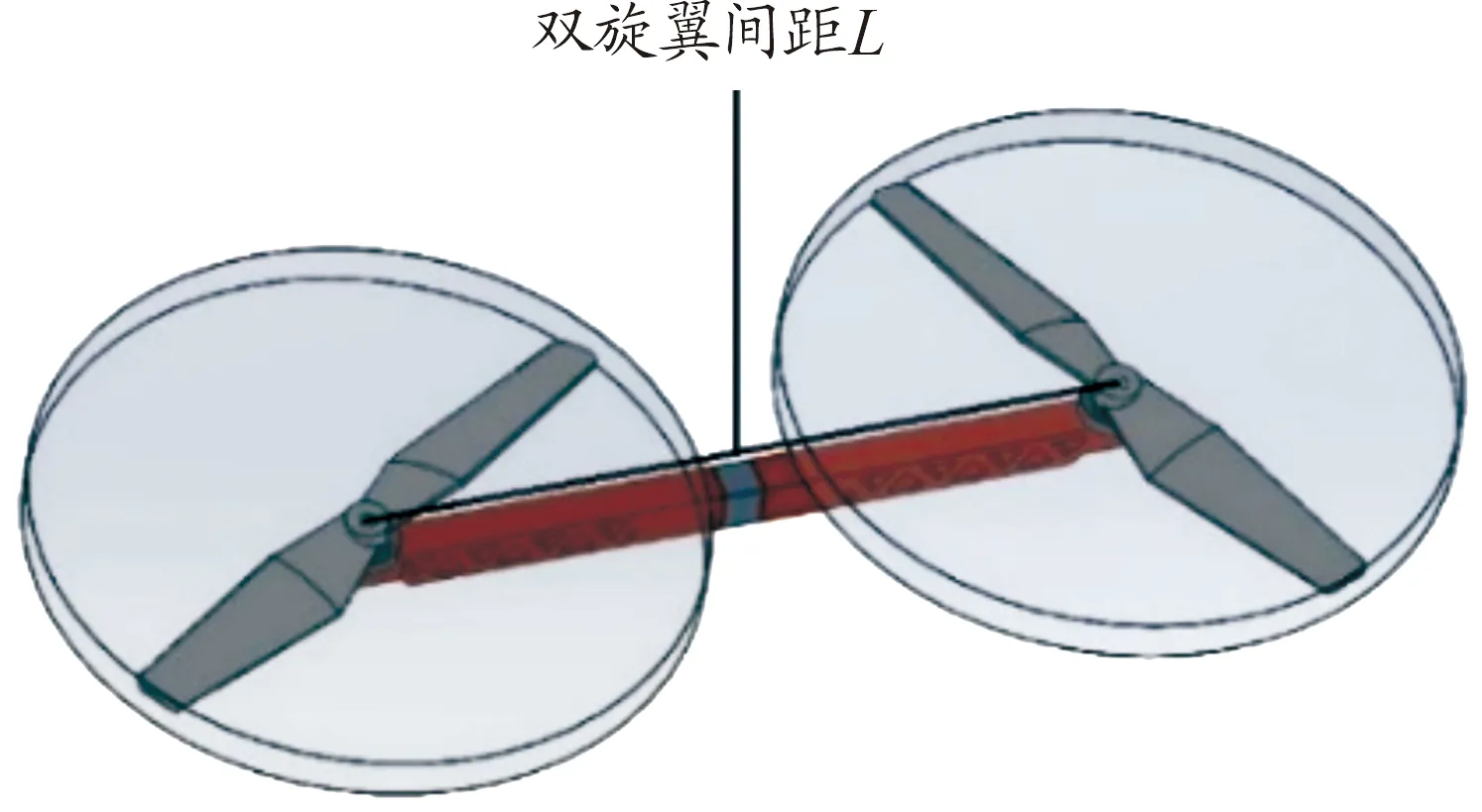
图4 双旋翼几何模型及对应旋翼间距示意图

考虑到悬浮子弹拟重(1 kg)情况和旋翼升力仿真结果与理论值准确度，由图2可得在18 000 r/min时，单旋翼可提供拉力为5.45 N，故同样选取双旋翼转速为18 000 r/min与单旋翼流场及气动力进行分析。

图5、图6分别为双旋翼在转速n=18 000 r/min时的速度矢量图和速度云图。

观察图5及图6可知：双旋翼速度矢量图和速度云图与单旋翼相比，双旋翼相邻处上方來流气体被旋翼拉扯分别吸入各个旋翼区域，且在各旋翼下洗流间存在复杂的相互干扰。旋翼下洗流区域呈现近端远离、远端相互诱导靠近的趋势[10]。

图5 转速n=18 000 r/min双旋翼速度矢量分布图

图6 转速n=18 000 r/min双旋翼速度云图

图7为旋翼转速为n=18 000 r/min时，旋翼间距L=2.1R的双旋翼与同转速的单旋翼旋转域上下表面压强比较图。观察图6、图7可知，由于翼间气动干扰，双旋翼旋转域上下表面压差小于单旋翼。

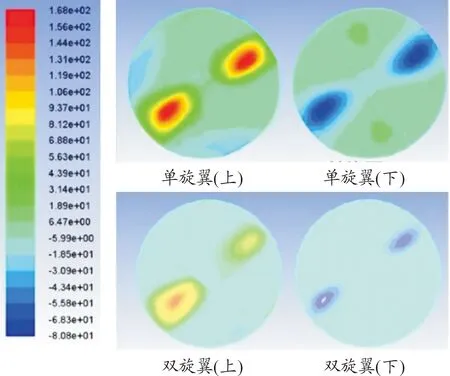
图7 n=18 000 r/min双旋翼与单旋翼旋转域压强云图

当双旋翼间距L改变时，旋翼所提供总升力与单旋翼升力无干扰叠加(10.9 N)结果如图8。

观察图8可知：当转速保持不变时，随着旋翼间距L的增加，双旋翼总升力先增大后减小，最终趋向于稳定，此规律符合双旋翼升力实验[10]的变化趋势，证明此次计算结果比较准确。当旋翼间距为2.1R时，双旋翼损失的升力最大，与单旋翼升力无干扰叠加结果相比降低了约9.2%；当旋翼间距为2.8R左右时，总升力相比单旋翼略提高0.9%；当旋翼间距大于3.1R左右时，双旋翼总升力与单旋翼升力无干扰叠加值基本相等。

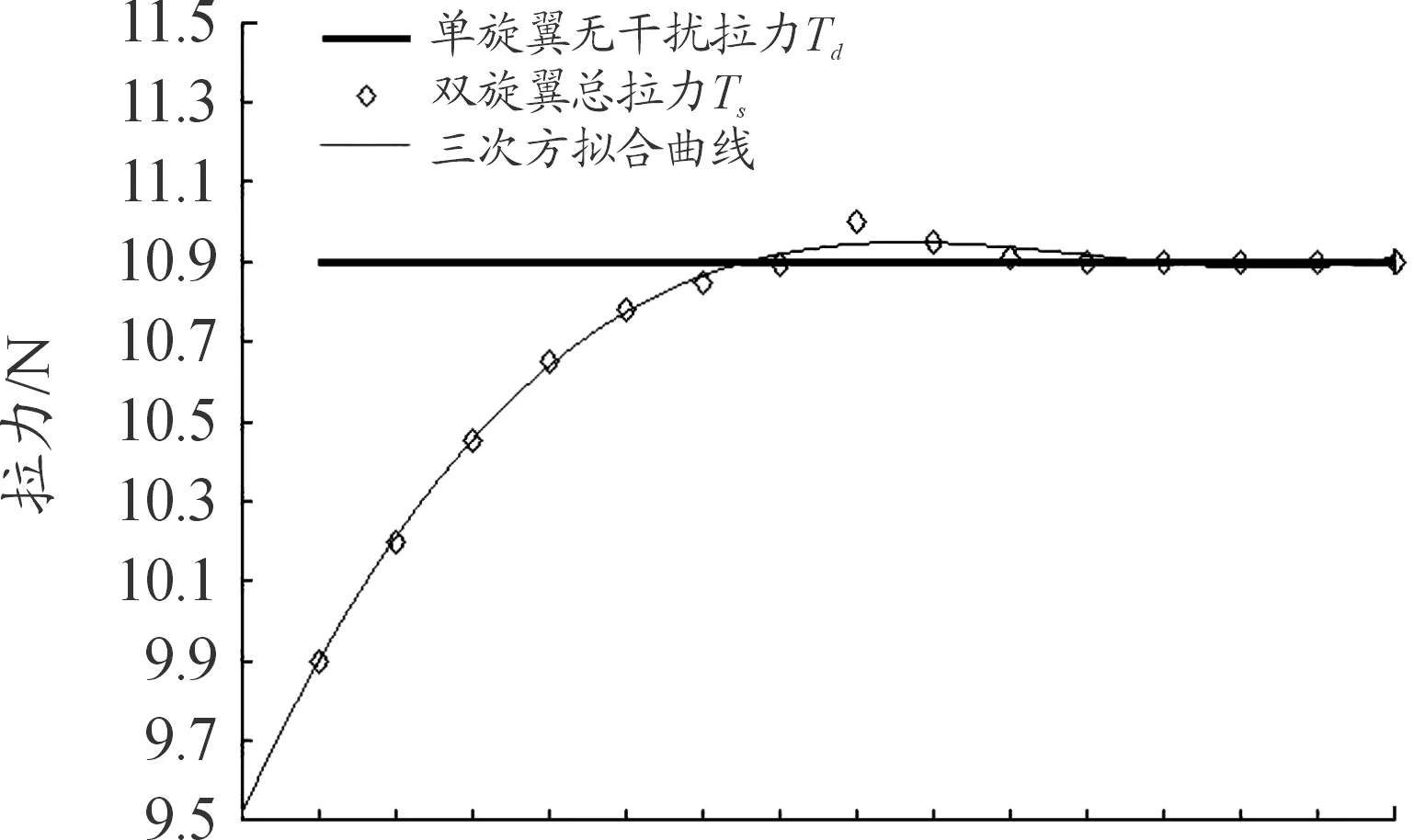
图8 双旋翼总拉力曲线

3.2 四旋翼气动干扰特性

对四旋翼进行几何建模如图9。与双旋翼不同，四旋翼的旋翼间距分为相邻旋翼间距L和对角旋翼间距L′。旋翼间的气动干扰不仅存在于相邻旋翼之间，当相邻旋翼间距L较小时，对角旋翼间同样存在较为复杂的气动干扰。

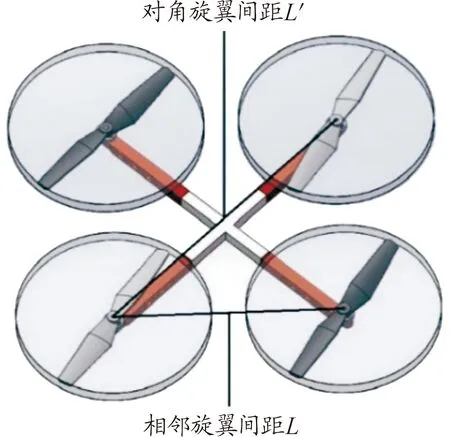
图9 四旋翼几何模型

同样考虑悬浮弹重量及所需升力，由图2可得在13 000 r/min时，单旋翼可提供拉力为2.71 N，故四旋翼转速选为13 000 r/min进行对比分析。由于四旋翼的旋翼间相互干扰类似双旋翼，故速度矢量图选取新的参考平面进行观察。如图10为四旋翼下方5 mm处速度矢量分布图。观察图可知：在间距较小时，四旋翼下洗流干扰不仅存在于相邻旋翼，对角旋翼也同样有下洗流间的干扰，各个旋翼受到3个干扰源，使得整个四旋翼流场更为复杂。

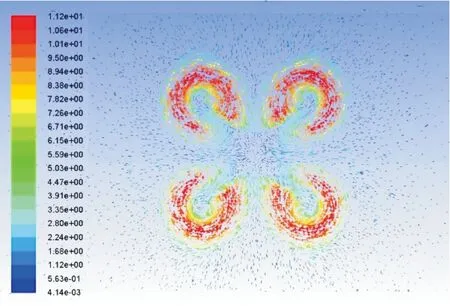
图10 四旋翼下方5 mm处速度矢量分布图

四旋翼成中心对称分布，同样通过控制相邻旋翼间距L的变化，四旋翼总升力与单旋翼升力无干扰叠加(10.84 N)如图11。

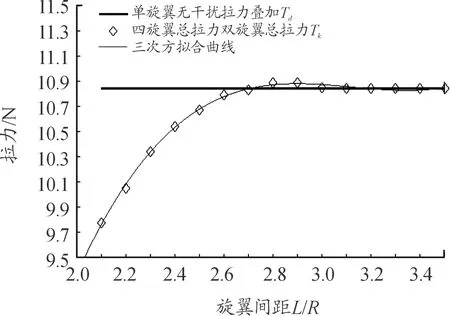
图11 四旋翼总拉力曲线

观察图11可知：四旋翼间距变化对总升力影响的规律与双旋翼基本相同。通过曲线拟合对双旋翼和四旋翼总拉力叠加值进行拟合，其值变化规律都基本符合三次方拟合曲线，故多旋翼的总升力随相邻旋翼间距增大而先增大后减小，最终趋于稳定。当旋翼间距为2.1R时，四旋翼升力损失较大与单旋翼升力无干扰叠加结果相比降低了约10%，大于双旋翼升力损失百分比(9.2%)；当旋翼间距为2.7R时，四旋翼总升力与单旋翼无干扰升力叠加基本相等，这与二旋翼特性相同；当旋翼间距为2.9R左右时，总升力相比单旋翼无干扰升力叠加值略提高0.8%；当旋翼间距大于3.1R左右时，四旋翼总升力与单旋翼升力无干扰叠加值基本相等。

由于“十”字分布式四旋翼，除两两相邻旋翼间的流场干扰外，对角旋翼同样存在流场间的相互干扰。因此当在较小旋翼间距时，对角旋翼间距同样较小，从而导致升力损失系数比双旋翼升力损失系数大很多。当旋翼间距在2.1R～2.7R区间内，随着旋翼间距的增加，四旋翼升力损失系数与二旋翼升力损失系数的差值逐渐变小，说明四旋翼间除了相邻旋翼间气动干扰逐渐减弱的同时，对角旋翼间气动干扰也逐渐变弱。当相邻旋翼间距大于2.8R时，对角旋翼间距大于3.1R，则相互干扰影响可忽略不计,此时各旋翼仅受相邻旋翼间的流场干扰，因此升力损失系数有所降低。而对于四旋翼“X”型分布，只需要考虑最近的相邻旋翼间距，其他相邻旋翼和对角旋翼间距值都较大，从而使得升力损失系数会有所降低。

4 结论

1) 对比GWS6030×2型旋翼的仿真结果和理论计算值，本文所采用的CFD仿真方法可以较准确地对小型旋翼进行数值仿真计算。

2) 在旋翼间的相互干扰下，旋翼下洗气流区域呈现近端远离、远端相互诱导靠近的趋势；相邻旋翼上方來流气流被分割，且气流速度相对降低，单个旋翼上下表面间压差变小，从而使得多旋翼总升力降低。

3) 以旋翼半径R为基准,旋翼间距在2R～3.1R区间内，多旋翼升力相对单旋翼会存在不同程度地升力损失。在相同转速下，当旋翼间距为2.1R～2.7R时，多旋翼的升力损失系数总体上随着旋翼间距的增大而逐渐降低；当旋翼间距为2.7R～2.9R时，旋翼间气动干扰相对较小，多旋翼总拉力略高于相应单旋翼无干扰拉力的叠加值；当旋翼间距大于3.1R时，旋翼间的气动干扰对装置悬浮能力影响可忽略不计。

4) 在相同间距和转速下，旋翼的个数和分布方式也会影响悬浮装置的升力损失系数。在相同转速和间距情况下，四旋翼“X”型分布式较“十”字分布式升力损失较小“十”字分布式四旋翼比双旋翼的升力损失系数更大。