一种基于灰色关联-可拓学的雷达导引头抗干扰性能评估方法

李尚生，张军涛，韩建立，但 波，王旭坤

(海军航空大学， 山东 烟台 264001)

1 引言

如何评价雷达导引头的抗干扰性能，对促进导弹作战性能提高具有重要意义。在复杂电磁对抗环境下，雷达导引头面对多变的干扰样式，衍生出多种抗干扰技术措施，使得对雷达导引头抗干扰能力的评估变得复杂。雷达导引头抗干扰性能常用的评估方法有模糊集法[1-2]、层次分析法[3-4]、支持向量机法[5]等。虽然这些方法都能对雷达导引头抗干扰性能的评估表现出特定的优势，得到不错的评估结果，但对于复杂的多指标评价问题，这些方法有一定的局限性[6]

可拓学理论，是对要解决的问题进行形式化的设计，既考虑到定性的方面，也兼顾到了定量方面[7]。评估对象的各特征由对象形式化来描述的物元理论，以及利用关联度分析将定性的描述转成定量的分析的可拓集合理论构成了可拓学理论，可拓学的评价方法建立在可拓学理论的基础之上，并广泛应用于各种领域[8]。灰色系统理论要对评估对象有精确的描述和准确的认识，就要利用已经知道的部分信息，对它们进行生成和开发。灰色关联分析建立在灰色理论的基础之上，计算评价方案与最优方案之间的关联度，评价方案的好坏等级由关联度的大小来确定[9]。在进行可拓学评价时，需要确定评价指标权重，由于评价指标的多样性和复杂性，仅凭单个专家在相关领域的知识储备和积累的经验来主观决策，得到的决策结果就不具有客观性和全面性，评估结果也不可靠[10]。为解决此问题，本文对雷达导引头的抗干扰性能指标进行分析，用灰色关联分析法确定评价指标权重，改进了只是通过专家主观赋权确定评价指标权重而带来的人为主观因素对评价结果的影响，对于几种典型雷达导引头用灰色关联-可拓学的评估方法进行了抗干扰性能评估，得到较为客观全面的评估结果。

2 雷达导引头抗干扰性能指标分析

雷达导引头抗干扰性能常用的评估准则有信息准则、功率准则、概率准则和效率准则。信息准则用在干扰背景下导引头信息的损失程度来衡量其抗干扰能力。功率准则采用雷达的信干比来描述其抗干扰能力，如压制系数K或抗干扰改善因子FEI来衡量[11]。概率准则是在干扰背景下，用完成抗干扰任务的概率来衡量抗干扰能力，如雷达抗干扰成功概率[12]。效率准则是同一性能指标在有无干扰条件下的变化来衡量抗干扰能力。要全面衡量雷达导引头的抗干扰性能，就要将不同的评估准则结合起来，综合运用不同的评估准则，对雷达导引头的固有抗干扰性能的选取依据进行分析，分析采取抗干扰措施后抗干扰性能的改善因子，建立雷达导引头抗干扰性能评价体系。如图1所示。

图1 雷达导引头抗干扰性能指标框图

2.1 雷达导引头综合抗干扰能力

雷达导引头的综合抗干扰能力表示为AJC=(PT0BSG)SASSSMSPSCSNSJ，其中，P表示雷达发射功率，T0表示雷达信号持续时间，BS表示雷达系统瞬时带宽，G表示雷达发射天线增益。SA、SS、SM、SP、SC、SN、SJ为采取各种抗干扰措施后的抗干扰改善因子，各参数的具体含义参照文献[13]。

2.2 雷达导引头的抗干扰效果度量

1) 抗干扰改善因子FEI[16]

雷达导引头在采取抗干扰措施后，其信干比会得到改善，改善程度用采取抗干扰措施与未采取抗干扰措施的信干比的比值来表示，即：

(1)

式(1)中：Sk、Jk分别为采取抗干扰措施后的信号功率和干扰功率；So、Jo分别为未采取抗干扰措施信号功率和干扰功率。

2) 抗欺骗式干扰有效概率CJ

抗欺骗性干扰的成功概率CJ用来度量抗干扰效果，即:

CJ=1-PAPBPC

(2)

式(2)中：PA是拖引式欺骗干扰成功概率；PB是点源非拖引式角度欺骗干扰成功概率；PC是假目标引导跟踪雷达概率。

3) 烧穿距离Rtb

对于给定的信干比Prs/Prj数值，将雷达能够检测和执行正确测量的距离定义为烧穿距离。

(3)

式(3)中：Pt为雷达峰值功率；Gt为雷达天线增益；Pj为干扰机发射功率；Gj为干扰机天线增益；σ为目标的RCS。

4) 测量精度改善因子PM

雷达导引头在采取抗干扰措施后，其测量精度会得到改善，改善的程度用采取抗干扰措施后与未采取抗干扰措施的测量精度的比值来表示。

(4)

式(4)中：MA为采取抗干扰措施后的测量精度；MB为未采取抗干扰措施的测量精度。

3 基于灰色关联-可拓学的数学评估型

灰色关联度分析的实质就是计算待评指标与参考指标的关联度，关联度越大，说明待评指标与参考指标的越接近。在可拓学的评价过程中，灰色关联分析对评价指标权重的确定，能够得到与理想权重接近的权重，降低人的主观性。基于灰色关联-可拓学的方法对雷达导引头抗干扰性能评估流程如图2所示。

图2 灰色关联-可拓学评估流程框图Fig.1 Grey relation-extenics evaluation flow chart

3.1 物元分析

分析待评对象的特征，建立物元模型R0，有：

(5)

式(5)中：N0为待评估状况等级；ci(i=1,2,…,n)为N0的特征；xi(i=1,2,…,n)为N0关于ci所取的特征值。

经典域确定如下：

(6)

式(6)中：Nj(j=1,2,…,m)为评估等级；ci(i=1,2,…,n)为对应评估等级的分项指标；Xji=〈aji,bji〉为评估等级Nj对于分项指标ci的取值范围，即经典域。

节域确定如下：

(7)

式(7)中：Np为全体评估等级；Xpi=[api,bpi]为指标ci对应于评估等级Np的取值范围，即节域。

3.2 综合权重确定

本文参照文献[3]，获取专家决策信息，通过专家在区间数打分来表示专家的不确定性，分数的大小是评价指标之间重要程度的体现，基于灰色关联法确定评价指标权重，相比于文献[6]可拓学进行评估时，通过专家的主观赋权确定评价指标权重。具体如下：K1名专家采用区间数对雷达导引头固有抗干扰性能的每个指标进行打分，得到决策矩阵Ak1，利用灰色关联分析的方法确定专家的权重V1，步骤如下：

步骤1熵权法求取指标权重。

计算离差矩阵D=(dij)n*n

(8)

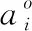
步骤2计算指标的熵值ei。

(9)

式(9)中，k为常数，j=1,2,…,n。当qij都相等时，即qij=1/n，此时熵值最大e=k×lnn=1，得k=1/lnn。

步骤3计算指标的偏离程度di。

di=1-ei

(10)

步骤4灰色关联度分析的方法确定专家的权重V1。

被比较序列与参考序列的关联系数为：

(11)

利用灰色关联分析的方法确定专家的权重，关联度为：

(12)

步骤5计算权重G1。

(13)

同样地，K2名专家对抗干扰效果度量的每个指标按照区间数进行打分，得到决策矩阵Ak2，利用灰色关联分析的方法确定专家的权重V2。

步骤6计算组合权重P。

P=(0.5G1,0.5G2)

(14)

3.3 计算关联度及确定评价等级

评价指标对应于评价等级的隶属程度的定量描述用关联度来表示。定义关联度为：

(15)

(16)

(17)

式(15)中，ρ(xi,Xpi)、ρ(xi,Xji)分别表示点xi与节域和经典域的距离。

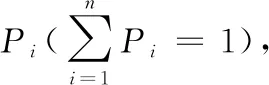
(18)

根据最大隶属度原则确定评价等级，Kj0(N0)=maxKj(N0)，j0∈(1,2,…,m)。

4 算例分析

4.1 物元分析

参照文献[5]中，6种型号雷达导引头抗干扰性能模糊化处理的抗干扰性能指标数据，对PAC-1、PAC-2、PAC-3、SA-10A、SA-10B、SA-2等6种型号雷达导引头综合抗干扰性能应用灰色关联-可拓学方法评估。

通过对评价指标数据分析，确定4个评价等级为：好(N1)、较好(N2)、一般(N3)、较差(N4)，划分每一评价等级对应评价指标的取值范围，确定各指标经典域。

评价指标节域为：

4.2 评价指标权重确定

邀请6位专家采用区间数对评价指标打分，通过灰色关联分析确定评价指标权重。前3位专家采用区间数法对雷达导引头固有抗干扰能力打分，后3位专家采用区间数法对抗干扰效果度量打分，决策矩阵如下：

针对区间数决策矩阵，按照综合权重里的步骤1对固有抗干扰性能计算离差矩阵，步骤2计算熵值矩阵，步骤3计算偏离程度矩阵归一化后求取指标权重，有：

W11=(0.329 7, 0.326 1, 0.139 2, 0.205 0)

W12=(0.141 2, 0.217 9, 0.316 4, 0.324 5)

W13=(0.087 6, 0.284 1, 0.138 0, 0.490 2)

按照步骤4的灰色关联法公式计算得到固有抗干扰性能关联度为R11=0.707 4，R12=0.772 5，R13=0.784 9，从而得到专家权重为：V1=(0.312 4,0.341 1,0.346 6)。

同理计算得到抗干扰效果度量的指标权重为：

W21=(0.388 9,0.388 9,0.068 7,0.153 5)

W22=(0.467 3,0.277 2,0.016 1,0.095 4)

W23=(0.0726,0.473 0,0.170 0,0.284 4)

灰色关联法公式计算得到抗干扰措施关联度为R21=0.553 2，R22=0.623 5，R23=0.907 6，从而得到专家权重V2=(0.258 0,0.290 7,0.451 3)。

计算得到综合权重为：

G1=(0.181 5,0.274 6,0.199 2，0.344 6)

G2=(0.212 7,0.242 5,0.336 4，0.259 1)

计算得到组合权重为：

P=(0.090 7,0.137 3,0.099 6，0.172 3，0.106 3，

0.122 2，0.1682，0.129 5)

4.3 评价等级确定

以PAC-1的雷达导引头抗干扰性能为例，计算PAC-1的雷达导引头抗干扰性能关于各等级的关联度，并进行等级评定。根据文献[5]提供的参数，PAC-1雷达导引头抗干扰性能表示成待评物元为：

利用式(15)计算关于各等级的关联度为：

K1(x1)=-0.600 5，K1(x2)=-0.400 7

K1(x3)=0.198 5，K1(x4)=-0.142 1

K2(x1)=-0.222 9，K2(x2)=-0.777 0

K2(x3)=-0.888 5，K2(x4)=-0.925 7

K3(x1)=-5.551 1，K3(x2)=0

K3(x3)=-0.500 0，K2(x4)=-0.666 7

K4(x1)=-0.704 0，K4(x2)=-0.556 0

K4(x3)=-0.1120，K4(x4)=0.112 0

K5(x1)=-0.214 4，K5(x2)=0.375 3

K5(x3)=-0.312 3，K5(x4)=-0.541 6

K6(x1)=-0.248 5，K6(x2)=0.494 0

K6(x3)=-0.253 0，K6(x4)=-0.502 0

K7(x1)=-0.324 9，K7(x2)=0.072 0

K7(x3)=-0.036 0，K7(x4)=-0.357 3

K8(x1)=-0.458 0，K8(x2)=-0.187 0

K8(x3)=0.374 0，K8(x4)=-0.278 0

按式(18)得到待评对象与各等级的综合关联度为：K1(p0)=-0.229 4，K2(p0)=-0.145 0，K3(p0)=-0.206 1，K4(p0)=-0.396 7。由于K2(p0)=maxKi(p0)，i=1,2,3,4，则判定p0属于第2等级，即PAC-1的雷达导引头抗干扰性能为较好。

如表1所示，计算其他型号雷达导引头抗干扰性能对各个评估等级的关联程度。同样，每一型号的雷达导引头抗干扰性能都可以被判定一个等级，如表2所示。

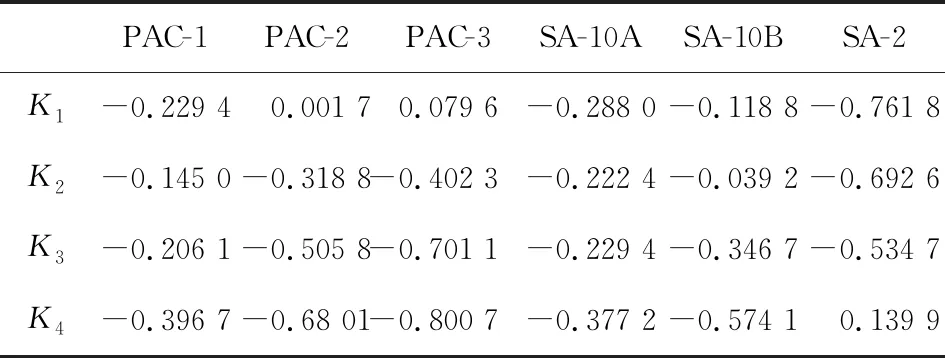
表1 各型号雷达导引头固有抗干扰性能关联度Table 1 Correlation degree of inherent anti-jamming performance of various types of radar seeker

表2 各型号雷达导引头抗干扰性能的等级判定Table 2 The grade judgment of anti-jamming performance of various types of radar seeker

4.4 计算结果分析

利用建立的灰色关联-可拓学的评价方法对几种典型雷达导引头抗干扰性能进行了综合等级评定，评定结果如表3所示，PAC-2、PAC-3、SA-10B的抗干扰能力评定等级为“好”，PAC-1、SA-10A的抗干扰能力评定为“较好”，SA-2的抗干扰能力评定为“较差”。相比于文献[5],该方法对SA-10B的抗干扰性能评估结论比SA-10A高一个等级，因为SA-10B是SA-10A的改进型，其制导精度和抗干扰性能都有改善。

表3 各型号雷达导引头抗干扰性能的等级对比Table 3 The grade comparison of anti-jamming performance of various types of radar seeker

5 结论

本文介绍了一种基于灰色关联-可拓学的雷达导引头抗干扰性能评估方法，该方法首先将雷达导引头的抗干扰性能划分为不同的等级，确定待评雷达导引头抗干扰性能的经典域、节域；其次应用区间数打分获取专家的决策信息，基于灰色关联法计算得到评价指标权重；最后将评价指标代入各评价等级进行关联度计算，得到综合关联度，并根据最大隶属度原则，得到雷达导引头抗干扰能力的评价等级。与其他的分析法相比，基于灰色关联-可拓学评估方法对雷达导引头抗干扰性能水平能够较全面地评估，灰色关联分析得到的权重比较客观。但是，由于抗干扰的评估指标涉及的要素多、评估准测多样，很难建立完备的评估体系，同时该方法只能确定评估等级，而确定了相同的评估等级后难以更好地区分优劣，需要完善和改进。