无后坐炮涡轮尾翼弹膛内流场数值模拟分析

郁家耀，蒋潇蓉，周君涛，何 永，薛 滨

(南京理工大学 机械工程学院， 南京 210094)

1 引言

无后坐炮是一种特殊火炮。在射击过程中利用火药燃气经过炮尾喷管后喷的反作用来消除炮身的后坐，使火炮达到平衡。付丽华等[1]建立了无后坐炮一维两相流内弹道模型，获得了膛内不同时刻的压力、速度分布。庞春桥等[2]通过实验方法对无后坐炮发射时的冲击波超压、热流强度以及燃气射流喷射时的气流冲量进行了综合测试。蒋潇蓉等[3]基于ADAMS建立了无后坐炮与三脚炮架的多刚体模型，对火炮的射击稳定性进行了分析。

滑膛式无后坐炮在发射增程破甲弹这种速度较高的弹丸时,常使用一种涡轮尾翼弹。涡轮尾翼弹出炮口后利用弹丸旋转产生离心力来张开尾翼，转速由无后坐炮后喷气流推动尾杆上的涡轮提供。张陈曦等[4]假设后喷气流为一维不可压缩流动，结合库塔-儒可夫斯基公式和半封闭弹道原理对弹丸转速进行了推导。

本文以一种涡轮尾翼弹无后坐炮为研究对象，利用计算流体力学方法耦合内弹道模型，对这种无后坐炮发射过程中的膛内流场进行研究。

2 物理模型

本文研究的82滑膛式无后坐炮的结构示意如图1所示。

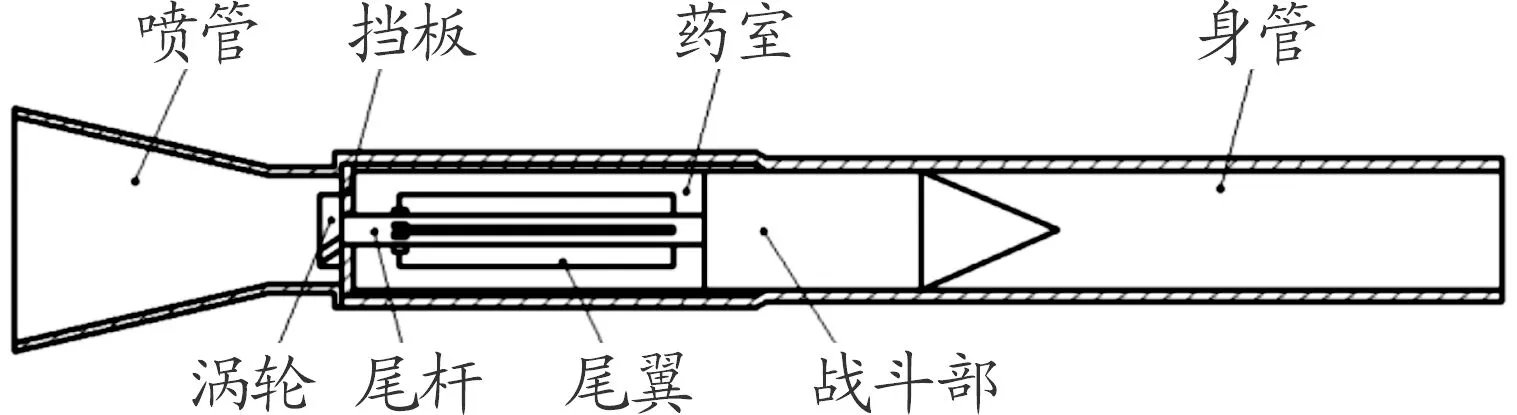
图1 结构示意图

这种存在涡轮结构的弹体在发射时，火药在药室内定容燃烧，药室内的火药气体一部分推动弹丸向前运动，另一部分通过涡轮流入炮膛并经过喷管喷出，从而构成了火药气体的二次膨胀过程。

3 数学方程

传统的经典内弹道模型，一般假设膛内火药气体为一维流动，而计算流体力学方法可以建立膛内火药气体流动的二维甚至三维模型。由于这种弹体存在涡轮的结构，为了分析这种结构所引起的弹道特点，利用计算流体力学软件Fluent，耦合经典内弹道模型对膛内二维流场进行分析。

3.1 经典内弹道模型[5-6]

建立适用于涡轮尾翼弹的经典内弹道模型如下：

几何燃烧定律方程为：

ψ=χZ-χλZ2

(1)

式(1)中：ψ为火药已燃百分比；Z为火药已燃相对厚度；λ与χ为火药形状特征量。

燃速方程为：

(2)

式(2)中：p为药室内压力；u1为燃速系数；e1为火药弧厚。

药室内压力为：

(3)

3.2 弹丸运动方程

以炮口方向为正方向，则靠近药室的一面为涡轮前壁，靠近喷管的一面为涡轮后壁。由于涡轮前后的压力不同，涡轮尾翼弹的弹丸运动速度受弹底压力与涡轮后壁压力的影响而不断变化。弹丸运动方程为:

(4)

式(4)中：S1为弹底面积；S2为涡轮后壁面积；p2为涡轮后壁所受压力。

3.3 计算流体力学方程[7]

基于膛内火药气体流动具有轴对称性质，建立火药气体流动的二维轴对称雷诺平均Navier-Stokes方程为：

(5)

式(5)中：ρ为气体密度；e为单位气体比内能；ur和uz分别为气体轴向与径向速度。

标准k-ε模型是工业上应用最广泛的湍流模型，其求解2个变量，湍流能量k和湍流能量耗散率ε，利用涡粘方法模拟雷诺应力，具有良好的收敛速率和相对较低的内存需求，但对于高时均应变流动会出现负的正应力这种非物理的结果，为避免这种情况，本文采用其改进型Realizablek-ε模型。

湍流能量输运方程可表示为：

τtijSij-ρε+φk

(6)

湍流能量耗散输运方程表示为：

(7)

式(7)中：右端项分别表示生成项、耗散项和壁面项；常数值为：Cε1=1.45，Cε2=1.92,σk=1.3。

4 耦合内弹道方程组的计算模型

4.1 边界条件及网格划分

忽略涡轮叶片旋转对气流的影响，并通过等效体积法将涡轮及尾部诸元件等效为圆柱体，建立二维轴对称流体计算模型如图2所示。

图2 膛内流场计算模型示意图

计算域总长度为501.4 mm，以喷管入口为交界面划分为2个区域，均采用四边形结构网格划分，最大网格尺寸1.5 mm，最小网格尺寸0.05 mm，共12 267个网格。身管、涡轮、尾杆、喷管壁面均假设为绝热无滑移壁面。药室底部设为压力入口边界，喷管出口设为压力出口边界，出口压力值由超音速气流压力外推得到。

4.2 耦合内弹道方程组

由文献[5]可知，涡轮尾翼弹的经典内弹道方程一般通过假定涡轮后方空间初始状态为真空，全由涡轮排气流出的气体填充，结合真空膨胀理论确定涡轮后壁压力并推导弹丸运动速度，这与真实情况误差较大。基于膛内气流运动的复杂性，本文采用Fluent与内弹道方程组双向耦合的方法，获得更符合真实情况的膛内流场，每个时间步之间与内弹道子程序进行数据交换。每一个时间步迭代开始前求解内弹道程序，将计算得到弹丸运动速度与压力数据等通过UDF传递至Fluent，迭代收敛后再通过UDF将气体流量与涡轮后壁压力代入内弹道方程组，再将计算得到的内弹道参数通过UDF传递至Fluent，……，依次循环直至弹丸飞出炮口[8-9]。耦合内弹道方程组的计算流程如图3所示。

图3 耦合内弹道方程组的计算流程框图

根据式(3)计算得到压力入口边界的压力值。式(3)中η的值通过F_FLUX宏函数读取涡轮排气断面网格节点的质量流量得到，传递至内弹道程序求解得到药室压力p，最后通过DEFINE_PROFILE宏函数定义为入口压力。

动网格运动速度由式(4)计算得到，利用F_P()宏获得涡轮后壁网格面压力，代入内弹道方程组得到弹丸运动速度，最后通过CG_MOTION宏函数赋值给区域B。

动网格方法采用区域整体运动结合动态层变的方法。区域A为网格变形区，区域B为刚性运动区。区域B以弹丸运动速度向右运动，并拉伸分裂交界面处的网格。

4.3 初始化

假设该无后坐炮药室压力达到5 MPa时，喷管打开并且弹丸起动。

流场计算由喷管打开开始，分别初始化药室内压力为 5 MPa，喷管内压力为标准大气压。时间步间隔0.001 ms。

5 流场仿真结果与分析

仿真结果显示，在弹丸起动约4.8 ms后，弹底到达炮口，炮口初速约为209.58 m/s，实验测得炮口初速为210.8 m/s，与实验值接近。

5.1 膛内压力与速度分析

图4、图5分别描述了不同时刻膛内压力与气流速度分布情况。无后坐炮射击时，药室内火药燃烧，使得膛压升高，高温高压气体经过涡轮和喷管喉部时速度加快，最后在喷管扩张段迅速膨胀。开始阶段，涡轮靠近喷管喉部，气流速度较小，火药气体受到涡轮的阻挡作用较大，导致压力在涡轮前壁面处达到最大。随着药室内火药燃烧，涡轮前后压力差不断增大，前后区域压力开始呈现明显的不同。当火药燃尽后，前后压力差减小，但涡轮后压力仍明显小于药室内压力。

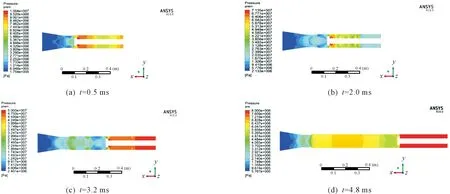
图4 同时刻膛内压力分布云图

图5 不同时刻膛内气流速度分布云图

在涡轮后壁面，由于涡轮快速向前运动与喉部入口的几何形状对火药气体的阻挡作用，涡轮后气体在这个区域存在回流现象，回流区域内出现旋转的涡流。且涡轮的运动还对后方气体产生类似“抽真空”的效果，使得涡轮后壁压力相对于其他区域较低，这也与实际情况比较吻合。

5.2 不平衡力与不平衡冲量

无后坐炮动不平衡是无后坐炮发射时“无后坐”实现系统平衡性能的重要指标。该滑膛式无后坐炮发射时，作用于炮身的不平衡力主要由气流作用于喷管喉部入口端面的轴向力与作用于喷管扩张段的推力组成[10]。

根据流场仿真结果处理得到的不平衡力变化曲线如图6所示。在整个膛内运动过程中，由于膛内气流的非定常流动，同一瞬间喷管与喷管喉部入口端面所受气流的轴向力不等，这种影响导致了整个炮身受到不平衡力的作用，整体上炮身所受不平衡力呈现出先增大后减小并趋于平缓的震荡过程，最大约为8 kN。

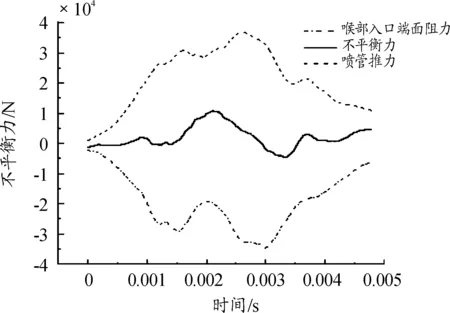
图6 不平衡力变化曲线

弹丸起动初期，膛内压力增加，气流对喉部入口端面的推力也不断增大，同时喷管扩张段受到的气流推力也不断增大。随着弹丸向前运动，涡轮远离喉部，喉部入口端面的气流在一段时间内受到涡轮后方涡流的影响，导致作用在端面上的压力骤降，不平衡力也因此达到最大。在经过一段时间后，随着涡轮继续向前运动，喷管推力与端面阻力重新增大，直到火药燃烧结束，膛内压力降低，喷管推力与端面阻力也随之降低，不平衡力曲线趋于平缓。

根据不平衡力计算整个膛内运动时期作用于炮身的不平衡冲量为：

实际应用中，对无后坐炮不平衡冲量的允许值大约为10 N·S，仿真计算得到的不平衡冲量的值与实际情况接近，可为结构的进一步优化提供理论依据。

6 结论

1) 计算流体力学与内弹道方程组的耦合模型，适用于涡轮尾翼弹无后坐炮的膛内流场计算，通过该方法可以观察到详细的膛内流场分布。

2) 涡轮结构对膛内火药气体有明显的阻挡作用，涡轮后气流处于涡流状态，涡轮后区域压力始终低于涡轮前区域压力。

3) 炮身所受不平衡力受到涡轮的影响，涡轮后方涡流导致短时间内喷管入口处火药燃气压力降低，不平衡力增大，该结论可对涡轮与身管的设计与优化提供参考。