配对设计中缺乏差值标准差情况下的样本量估计策略*

南方医科大学公共卫生学院生物统计学系(510515) 邢 星 吴 莹 陈平雁

【提 要】 目的 在临床配对设计试验中，利用定量指标变化值(干预前后差值)进行两组比较时，其样本量的准确估计需要依据两组变化值的均数和标准差。如果参数假设源于外部数据的话，通常会缺少变化值的标准差信息。本研究旨在探索配对设计中缺乏差值标准差情况下的样本量估计策略。方法 两组变化值的均数可直接从干预前均数与干预后均数相减得到。经理论推导，假设两组方差齐性，变化值的标准差可利用干预前后的相关系数与原数据共同标准差求得。结果 在配对设计中缺少变化值的标准差的情况下，如何准确估计样本量实质上是一个如何准确估计干预前后测量值的相关系数的问题。如果相关系数高估，则导致检验效能偏低，即样本量相对不足；如果相关系数低估，则导致检验效能升高，使得样本量过大而造成浪费。结论 缺乏差值标准差的配对设计在进行样本量估计时应借助相关程度来提高样本量估计的有效性。

在配对设计临床试验中，定量指标的干预前后变化值是常见的疗效评价指标。对于此类指标两组比较的样本量估计，除了需要确定检验水准和检验效能外，还需设置变化值的均数和标准差参数。如果参数假设源于外部数据(如文献报道)，通常会缺少变化值的标准差信息，难以准确估计样本量。本研究旨在探索在配对设计中缺乏差值标准差情况下的样本量估计策略。

方 法

样本量的估计原理通常基于检验统计量和H1假设进行反推[1-4]。对于定量指标，假设给定模型参数θ的函数f(θ)为效应量指标，T表示f(θ)的无偏估计统计量，测量值服从正态分布且满足两组方差齐性，则有

(1)

如采用双侧检验，给定检验水准α及检验效能1-β。

在H0假设下f(θ)=0，α水平下针对H0的检验界值为

(2)

(3)

(4)

在两组方差齐性假设下，令σ2为原数据的共同方差，则有[5]

(5)

其中，ρ为干预前与干预后测量值的总体相关系数。

结 果

临床实际中，通常0<ρ<1。当ρ=0.5时，σd=σ，此时用σ估计样本量与理论估计的样本量一样；当ρ<0.5时，σd>σ；此时用σ估计样本量较理论估计的样本量要大；当ρ>0.5时，σd<σ；此时用σ估计样本量较理论估计的样本量要小。因此，在缺少变化值的标准差的情况下，如何准确估计样本量实质上是一个如何准确估计干预前后测量值的相关系数的问题。如果相关系数高估，则导致检验效能偏低，即样本量相对不足；如果相关系数低估，则导致检验效能升高，使得样本量过大而造成浪费。

设定双侧检验水准α为0.05，检验效能1-β为90%；两组变化量之差值的总体均数μd从0.2到0.8，间隔0.1；两组差值的总体标准差σd相同，均为1.0，即效应量μd/σd从0.2到0.8，间隔0.1。根据公式(4)和公式(5)，计算得到配对设计试验中不同效应量和相关系数所对应的每组样本量(表1)。例如，当检验效能为0.9、真实的相关系数(总体相关系数)为0.4、效应量为0.5时，正确的样本量为53。如果计算样本量时效应量按0.5估计，总体相关系数按0.5估计所求得的样本量为44，比正确的样本量低估9例；如果总体相关系数按0.3估计，则样本量为61，比正确的样本量高估8例。由表1可见，相关系数每高估或低估0.1，样本量会相应地低估或高估约10%以上。图1描述了不同相关系数和效应量所对应的样本量，可见随着相关系数增大和/或效应量的增大，样本量呈减小趋势。

表1 干预前后变量的相关系数和效应量估计对每组样本量估计的影响

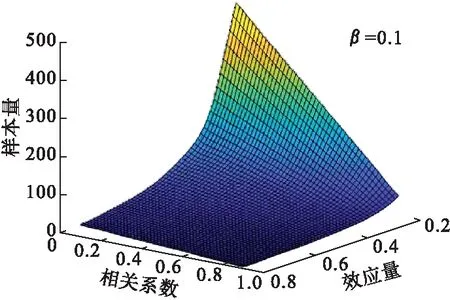
图1 干预前后变量的不同相关系数和效应量估计的样本量

讨论与结论

本文所提出的策略也适用于定量指标两组配对设计的样本量估计。虽然文中列举了两组样本量均衡的情况，在两组样本量比例不同时，基于本研究对变化值标准差的估计策略带入相应样本量估计公式即可。

对于定量指标两组比较的临床试验设计，在缺少变化值标准差信息的情况下，如果直接利用原始测量值的标准差进行样本量估计，则其结果将以干预前后相关系数0.5为界呈现检验效能不足或效能过高(即浪费样本量)的问题。

在缺少变化值的标准差的情况下，如何准确估计样本量实质上是一个如何准确估计干预前后测量值的相关系数的问题。在获得总体标准差后，研究者可通过估计配对数据间的相关系数，计算较为准确的样本量估计值。如果相关系数高估，则导致检验效能偏低，即样本量相对不足；如果相关系数低估，则导致检验效能升高，使得样本量过大而造成浪费。