面板计数数据的非参数样条估计*

上海交通大学生命科学技术学院生物信息与生物统计系(200240) 秦 飞 俞章盛

【提 要】 目的 建立更为一般化的面板计数数据模型，既包含具有时变效应的协变量又包含具有非参数效应的协变量。方法 使用伪似然样条估计方法及全似然样条估计方法，并通过数值模拟定性和定量地比较这两种方法。结果 两估计方法在样本量为200时都具有很小的偏差和均方误差(MSE)；全似然样条估计方法的偏差和MSE更小(比伪似然样条估计方法的MSE小约35%)，但计算时间远远超过伪似然样条估计方法(约是其200倍)；两种估计方法用于小儿哮喘数据后得到了相似的估计结果，揭示了白细胞介素IL-9的时变效应及白细胞介素IL-5的非参数效应。结论 综合MSE及计算时间，在此模型下本研究更推荐使用伪似然样条估计方法。

面板计数数据经常出现在电子医疗病例、临床试验、流行病学研究中。对于面板计数数据，研究者仅调查到在两次相邻的观测时间点间复发性事件发生的次数，但未调查到复发性事件发生的具体时刻。一个典型的例子可见于小儿哮喘研究[1]。在此研究中，研究人员对105个小儿哮喘病患者连续跟踪了5年，通过电话随访获得截至到此刻小儿哮喘复发的次数，但未调查到复发的具体时刻，所以收集到的数据为面板计数数据。

在对面板计数数据的建模方面，Zhao等[2-3]先后建立了具有时变效应及具有非参数效应协变量的面板计数数据模型，但尚未有研究在一个面板计数数据模型中同时考虑到这两者，而这种情况在实际应用中是可能出现的，比如Cai等[4]就在Cox模型中同时包括了具有时变效应及具有非参数效应的协变量。在估计方面，Zhao等[2-3]仅采用了伪似然函数下的样条估计方法，但没有采用全似然函数下的样条估计方法。因此，本文将建立同时含有时变效应及非参数效应协变量的面板计数数据模型，采用伪似然样条估计及全似然样条估计的方法并对其进行对比，最后将此方法应用于小儿哮喘研究中[1]。

模型及估计

1.模型

对于面板计数数据，研究者可以观测到n个独立的样本Ui=(Ki，Ti，N(i)，Xi，Zi)，i=1，2，…，n，其中Ki为观测次数，Ti={Ti，1，Ti，2，…，Ti，Ki}为观测时间点，N(i)={N(Ti，1)，N(Ti，2)，…，N(Ti，Ki)}为面板计数值，Xi=(Xi，1，Xi，2，…，Xi，p)T为具有时变效应的协变量，Zi=(Zi，1，Zi，2，…，Zi，q)T为具有非参数效应的协变量。类似于其他非参数模型，本文假定某个协变量是具有时变效应还是非参数效应是提前设定好的。本文建立以下非参数模型：

E[N(i)(t)]=Λ0(t)·exp[(β1(t)T·Xi+β2(Zi)]

(1)

其中，Λ0(t)为单调非减的非负函数，β1(t)=(β1，1(t)，β1，2(t)，…，β1，p(t))T为时变系数，β2(Zi)=β2，1(Zi，1)+β2，2(Zi，2)+…+β2，q(Zi，q)为非参数效应。本文仅呈现当p=q=1时的情形，本文的估计方法很容易拓展到p，q>1的情形。

2.样条函数

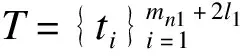
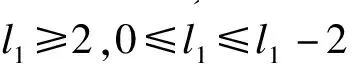
(2)

(3)

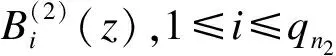
(4)

3.伪似然估计

正如Zhang等[5-6，14-15]所述，首先假设潜在的计数过程{N(t)：t≥0}为非齐次的泊松过程，然后忽略每个个体的计数数据{N(Ti，1)，N(Ti，2)，…，N(Ti，Ki)}之间的相关性从而得到的伪似然估计量通常具有渐近正态性和相合性。参照Zhang等[5-6，14-15]的思路，本文建立模型(1)的伪似然函数如下：

L(1)=P[N(T1，1)=N1，1，N(T1，2)=N1，2，…，N(T1，K1)=N1，K1，…，N(Tn，1)=Nn，1，…]

对L(1)取对数并忽略无关项，然后将样条近似式(2)～(4)代入，得到以下对数伪似然函数：

(5)

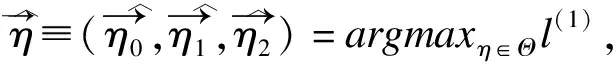
4.全似然估计

如Zhang等[5-6，14-15]所述，全似然估计量通常要比伪似然估计量估得更准但同时计算量更大。本文也探讨了全似然估计在模型(1)下的表现。全似然估计量是通过首先假设潜在的计数过程为非齐次泊松过程，然后利用面板计数数据增量间的独立性而构造。本文建立模型(1)的全似然估计函数如下：

exp[-[Λ0(Ti，j)·exp(β1(Ti，j)·Xi+β2(Zi))-Λ0(Ti，j-1)·

exp(β1(Ti，j-1)·Xi+β2(Zi))]]}

其中，Λ0(Ti，0)≡0，Ni，0≡0。对L(2)取对数忽略并无关项，然后将样条近似式(2)～(4)代入，得到以下对数全似然函数：

(6)

同样地，极大化式(6)便可得到参数的全似然估计。这一过程仍可通过相同的R函数constrOptim()来实现。

模拟研究

N(Ti，j)-N(Ti，j-1)～Po{Λ0(Ti，j)·exp[β1(Ti，j)·Xi+β2(Zi)]-Λ0(Ti，j-1)·exp[β1(Ti，j-1)·Xi+β2(Zi)]}

其中j=1，…，Ki，Ti，0≡0，N(Ti，0)≡0，Λ0(0)≡0。本文对真实函数设置以下两种情形：

情形1：Λ0(t)=t+1，β1(t)=1.5·sin(0.05·πt)，β2(z)=sin(πz)；

情形2：Λ0(t)=t+1，β1(t)=0.15·t，β2(z)=sin(2πz)·I(z≤0.5)+0.5·sin(2πz)，其中I(·)为示性函数。可以看到情形2要比情形1更为复杂。

本文设置样本量为50及200，产生500次蒙特卡洛数据。参照Lu等[5-6]的做法，本文使用三次样条，样条的内部节点数设置为6，采用分位数的方法放置节点，即选择所有不同观测时间点的k/(m+1)分位点(k=0，1，…，m+1)为这m+2个节点的放置位置。

图1展示了情形1下样本量为50时对这三个函数Λ0(t)，β1(t)，β2(z)500次估计的均值曲线及2.5%，97.5%分位数曲线。从图1可以看出，这两种方法的估计结果都存在一定的偏离，也如前文所预料，这三个函数的全似然估计的均值曲线更接近于真实曲线，且置信区间更窄。当样本量增大为200时，所有的均值曲线相对样本量为50时都更接近真实曲线且置信区间更窄，全似然估计方法此时仍旧估得更准且置信区间更窄，但同时也注意到此时两方法的均值曲线都几乎跟真实曲线重合(图2)。

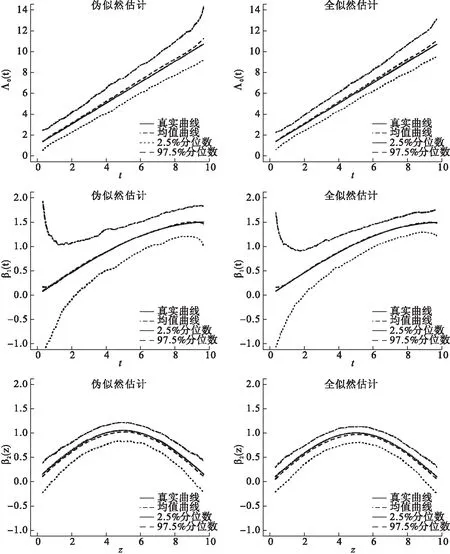
图1 情形1，样本量为50时的估计结果

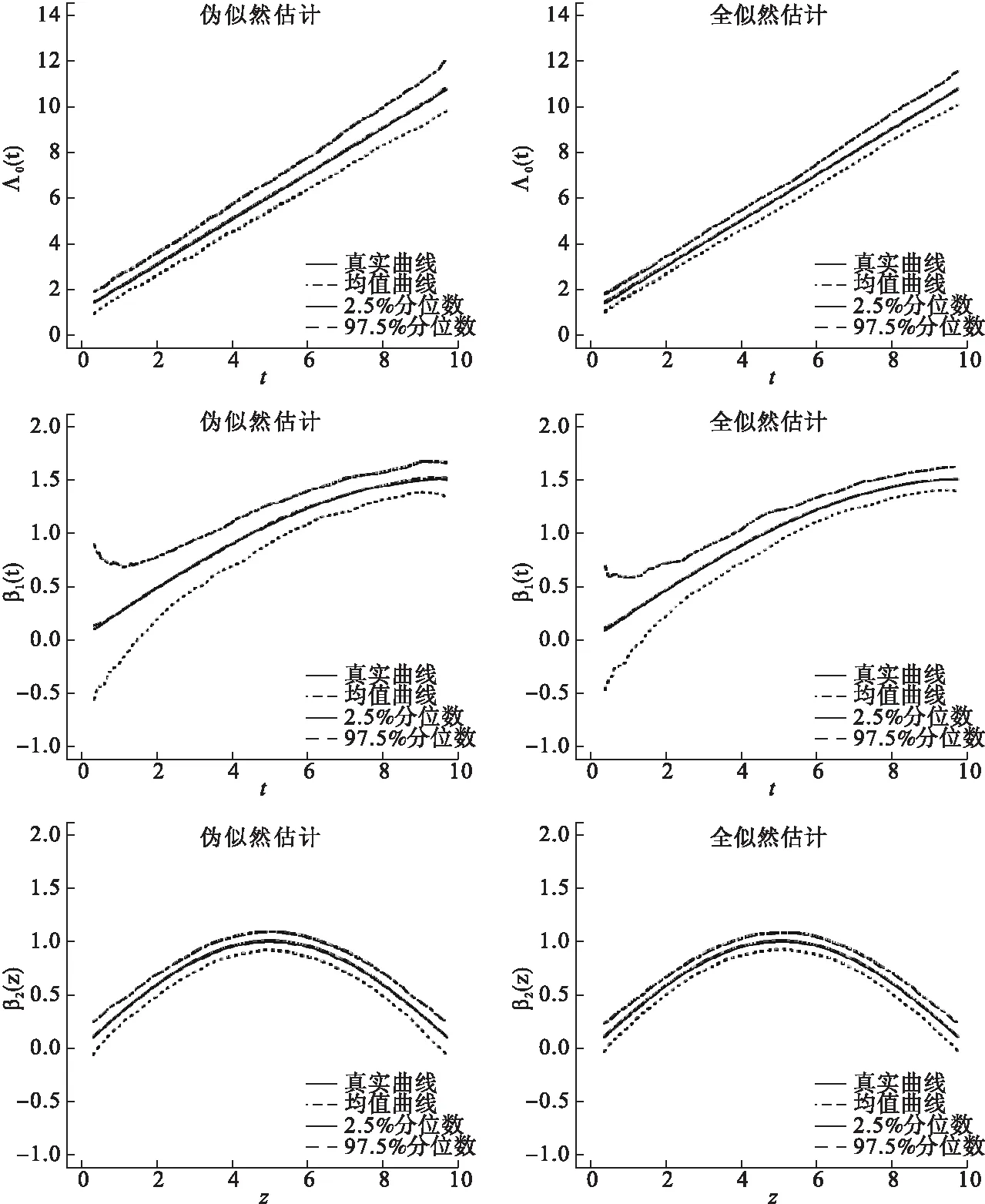
图2 情形1，样本量为200时的估计结果

本文也对这两种估计量进行了定量比较。从表1可以看出，当样本量为50时，全似然估计下这三个函数的估计偏差、均方误差均小于伪似然估计，但伪似然估计的计算时间远远小于全似然估计。当样本量增大为200时，这两种估计下函数的估计偏差、均方误差都大大减小，全似然估计方法仍估得更准，但同时计算时间方面伪似然估计方法仍远具优势，并且也注意到此时两估计方法的偏差几乎可以忽略。情形2的模拟结果和结论类似情形1，由于篇幅有限，本文没有展示。由于在接下来的实际应用中样本量为105，本文还做了上述两情形下在样本量为100时的模拟，此时的估计偏差、均方误差及计算时间介于样本量为50时的结果和样本量为200时的结果之间，得到的结论也类似(由于篇幅有限，未展示)。总之，就估计的准确性和稳定性而言，全似然估计方法优于伪似然估计方法，前者的TMSE比后者小约35%。但就计算时间而言，伪似然估计占绝对优势(全似然估计计算时间约为伪似然的200倍)，再加上当样本量为200时，伪似然估计量已非常接近真实函数，所以在模型(1)下，本文推荐使用伪似然估计方法。

表1 情形1下两种估计量的定量比较结果

实例应用

本部分把前文介绍的方法应用到小儿哮喘研究中，该研究的总体描述可参考文献[1]。该研究旨在探究免疫因子特征和小儿哮喘之间的关系，纳入了105名小儿哮喘患者，平均入组年龄为10.9月，50.5%的患者是女性，9.5%的患者母亲在怀孕时抽烟。

白细胞介素IL-9是CD4+辅助细胞分泌的一种细胞因子，对哮喘小鼠模型的遗传学研究表明，该细胞因子是支气管高反应性发病的决定性因素[16]。根据临床经验，有很多因素都会影响到小儿哮喘而且它们的影响效果会随着时间的变化而变化，因此本文设定IL-9具有时变效应。此外，另一种白细胞介素IL-5一直与过敏性鼻炎、哮喘等多种变应性疾病相关[17]。根据Zhao等[3]的研究结果，IL-5具有明显的非参数效应。因此，在本文的面板计数数据模型中包括性别及是否吸烟这两个协变量后，本文用伪似然估计和全似然估计这两种方法来估计IL-9的时变效应及IL-5的非参数效应。

本文使用三次样条来估计模型中的未知函数；使用AIC准则(AIC=-2·l(η)+2k)来选择内部节点个数，其中l(η)为对数伪似然函数值或者对数全似然函数值，k为模型中参数的个数；和模拟研究类似，节点的位置选取依旧使用分位数的方法。对于伪似然估计，本研究选择的节点数为7，对于全似然估计，选择到的节点数为6，对时变效应β1(t)和非参数效应β2(z)的估计结果如图3所示。从图3可以看出，由于使用的内部节点数更多，伪似然估计方法对β1(t)及β2(z)的估计曲线更震荡些，但总体趋势和全似然估计方法得到的曲线十分相似。这两种估计结果都揭示了IL-9对小儿哮喘效应的时变性，即在30个月龄之前，效应随着年龄的增大而增大，但其后效应基本趋于平稳。同之前Zhao等[3]的研究结果一致，IL-5的效应仍旧是非参数的，效应随着IL-5值的增大而增大。本研究中模拟及实例应用部分是在R软件中实施的，实例应用部分的代码可通过以下ftp地址获得：ftp：//public.sjtu.edu.cn/(用户名yuzhangsheng，密码public)。

图3 小儿哮喘研究中对白细胞介素IL-9及IL-5的估计结果

小 结

本文建立了更为一般化的面板计数数据模型，其既包含具有时变效应的协变量，也包含具有非参数效应的协变量；本文使用了伪似然样条估计方法和全似然样条估计方法，并将这两种估计方法进行了对比；最后分析了小儿哮喘研究数据。

在模拟研究部分，发现当样本量为50和100时，这两种估计方法都存在一定的偏差，但全似然样条估计方法的偏差和均方误差更小；同时由于全似然函数更为复杂，所以全似然样条估计方法具有更长的计算时间。当样本量增大到200时，两种估计方法都具有可以忽略的偏差，且全似然样条估计方法仍旧具有更小的偏差和均方误差，但同时计算时间也长得多。综合均方误差和计算时间，且考虑到当样本量为200时伪似然样条估计方法已较准确，本文推荐在类似的模型中使用伪似然样条估计方法。

在实例应用部分，这两种估计方法得到了类似的估计结果，都揭示了白细胞介素IL-9的时变效应及白细胞介素IL-5的非参数效应，此结论也跟之前的研究[3]一致。探究在本文模型下两种估计方法的理论性质，研究更为高效的算法将是我们未来的研究方向。