基于MSET的压气机故障预警研究

陆永卿, 涂 雷, 茅大钧

(1.上海华电奉贤热电有限公司, 上海 201403; 2.上海电力大学, 上海 200090)

压气机作为燃气轮机的主要部件之一,由于受到来自机组内部恶劣工况和周围环境污染的影响,随着运行时间的增加,可能产生不同程度的性能衰退或损伤,阻碍设备的正常运行,甚至造成各种严重事故的发生[1-2]。压气机常见故障有压气机叶片磨损、压气机顶端间隙增大和压气机喘振等。因此,对压气机进行预警监测,能够提高检修效率,减少经济损失。

随着计算机技术的快速发展,对压气机的故障预警和诊断已有一定的研究。文献[3]应用能量比方法成功地对不同换算转速下的轴流压气机喘振故障进行了诊断。文献[4]建立了燃气轮机性能仿真模型,在模型中考虑实际环境参数的波动范围,对参数归一化处理并对燃气轮机气路参数进行故障预警。文献[5]应用基于神经网络的线性拟合方法,建立了压气机离散模型。

目前的研究成果主要集中在风机故障诊断方面,而对风机故障预警的研究较少。由于风机设备本身构造复杂、故障类型繁多,故障与征兆之间的关系未知,且设备运行过程会受到许多不确定因素和随机干扰的影响,使得实现准确故障预警较为困难。多元状态估计技术(Multivariate State Estimition,MSET)的出现为压气机故障预警提供了新的思路[6]。MSET实质上是一种先进模式识别方法,通过涵盖正常运行状态的数据进行相似性建模。与传统的神经网络方法相比,MSET具有建模过程简单、物理意义明确等优点,可以满足工业现场实时性要求[7]。

本文利用MSET对压气机的运行数据进行分析,研究压气机运行过程中状态变量之间的相关性,建立故障预警模型,分别用压气机正常状态和故障状态下的数据对模型进行测试。实验结果表明,本文提出的故障预警模型具有一定的应用效果。

1 多元状态估计技术

MSET最早是美国阿尔贡国立实验室为了检测核电厂中传感器、设备以及运行参数的初始劣化点而开发的一种非参数建模方法,是一种利用正常运行状态下监测参数之间的相似性来实现状态估计的先进模式识别技术[8]。其本质是利用对象正常运行状态的历史数据,充分挖掘各参数之间的关系,依据所获得的数据估计对象的真实状态。

利用从正常运行状态中得到的历史数据构成矩阵,即历史记忆矩阵D。矩阵的每一列均代表一个观测状态,矩阵的列数m代表m个状态,行数n代表每次观测的n个变量。假设某一过程或设备的监测变量中共有n个相互关联的变量,则将在某一时刻tj观测到的此n个变量记为观测向量,为

X(tj)=[x1(tj)x2(tj)x3(tj) …xn(tj)]T

(1)

式中:xi(tj)——测点i在tj时刻的测量值,i=1,2,3,…,n。

历史记忆矩阵D可表示为

(2)

历史记忆矩阵D是MSET的基础,也称为MSET的系统模型[9]。历史记忆矩阵中的每一列观测向量代表设备的一个正常运行状态,经过合理选择的历史记忆矩阵中的m个历史观测向量所形成的子空间能够代表过程或设备正常运行的整个动态过程。

对于某一时刻设备的观测向量Xobs,MSET将此状态与历史记忆矩阵中存储的运行状态进行比较,并计算出对当前系统状态的估计向量Xest,估计向量为历史记忆矩阵D与权值向量W的积,为

Xest=DW=D[w1w2w3…wm]T=

w1X(t1)+w2X(t2)+…+

wmX(tm)

(3)

MSET的估计向量为历史记忆矩阵中m个历史观测向量的线性组合。权值向量W代表此状态与历史记忆矩阵中状态的一种相似性测度。权值向量可通过最小化残差向量ε来获得。观测向量Xobs和估计向量Xest之间的残差为

ε=Xest-Xobs

(4)

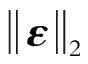
(5)

本文选用欧氏距离运算[10],其中,xi和yi为变量。即

(6)

式中:X,Y——观测向量与估计向量。

式(6)可以反映2个数据向量之间的相似程度。将式(5)代入式(3)可以推导出估计向量为

(7)

2 偏离度和预警阈值

利用与观测向量和估计向量有关的偏离度函数可以定量衡量观测向量与估计向量之间的偏离程度,在此基础上利用滑动窗口法设定合理的预警阈值。

2.1 偏离度

MSET的观测值与估计值之间的残差可以反映设备异常或故障。通常直接将某变量的观测值与其估计值之间的残差作为故障判断指标[11]。欧氏距离是衡量2个向量之间偏离程度最常用的方法。在此基础上定义偏离度函数为

(8)

式中:w′i——观测向量中第i个变量的权重系数。

偏离度越大,说明向量X和Y的偏离程度越大;而偏离度越小,则说明向量X和Y的偏离程度越小。当偏离度等于零时,向量X与Y相等。

2.2 预警阈值

利用滑动窗口法消除压气机运行中的不确定因素和随机干扰,提高故障预警的准确率。通过选择合理的滑动窗口宽度,能够及时、快速地捕捉偏离度统计特性的连续变化,消除随机因素的影响[12],提高设备状态监测的可靠性,降低误报警的几率。当压气机运行异常时,这些状态模型可及时检测出压气机状态的轻微异常变化,从而实现故障预警。

假设在某段时间内,基于MSET的估计偏离度序列共n个,则

S(Xobs,Xest)=[S1,S2,S3,…,SN,…Sn]

(9)

对该序列取一个宽度为N的滑动窗口,如图1所示。窗口内连续N个偏离度的平均值为

图1 滑动窗口法

(10)

根据偏离度平均值确定故障预警阈值EAN。压气机正常运行时MSET模型的平均偏离度最大值为EN,k为预警阈值函数,则风机故障的预警阈值为

EAN=kEN

(11)

3 基于MSET的压气机故障预警模型建立

3.1 变量的选取

由于压气机相关变量众多,如果将这些变量都作为相关变量,将会出现冗余,造成不必要的计算量,增加模型的复杂度,因此需要对这些变量进行筛选。结合压气机故障分析资料,最终选取机组负荷、大气压力、相对湿度、进气滤网压差、喇叭口静压、压气机进口压力、压气机进气温度、IGV开度、压气机进气流量、压气机压比、排气压力等11个相关变量组成观测向量[13-15]。

3.2 数据预处理

由于选取的11个变量的数据绝对值相差很大,为保证非线性运算符能正确衡量不同观测向量之间的欧氏距离,需要对数据进行预处理。采用标准化处理原始数据,可以避免确定各变量的极大值和极小值,降低离群点的影响。设观测向量中变量x的均值为μ,标准差为σ,则标准化公式为

(12)

式中:x′——变量x的标准化值。

4 实例仿真

选取上海某热电厂的压气机故障前一段正常运行状态历史数据构成历史记忆矩阵,建立故障前压气机模型。从热电厂PI实时数据库中选取2019年4月21日0:00到2019年5月8日0:00共2 000个正常运行状态历史数据构成D矩阵。选取故障前140个数据作为观测向量集。计算观测向量集和估计向量集之间的偏离度。为了方便计算,权重系数w′i取1。观测向量集的偏离度如图2所示。

图2 观测向量集的偏离度

由图2可知,从第110个数据点开始,偏离度有逐渐增大的趋势。这说明第110个数据点是故障发生的早期时间,真正故障发生在第140个数据点左右。

由于篇幅有限,本文以压气机的进气温度和进气滤网压差2个参数进行实例仿真。仿真结果如图3～图6所示。

图3 进气温度仿真

图4 进气温度估计残差

图5 进气滤网压差仿真

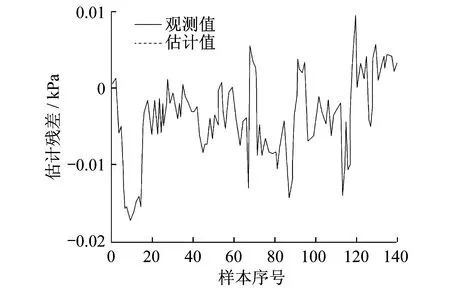
图6 进气滤网压差估计残差

由图4可知,压气机进气温度在正常运行状态下的估计残差小于0.2 K。由图6可知,压气机进气滤网压差在正常运行状态下的估计残差小于0.02 kPa。上述仿真表明,2个变量的估计残差值都比较小,说明MSET模型具有很高的精确度。

针对压气机运行中的不确定因素和随机干扰问题,利用滑动窗口法进行消除。选取的滑动窗口宽度为10,得到平均偏离度曲线如图7所示。

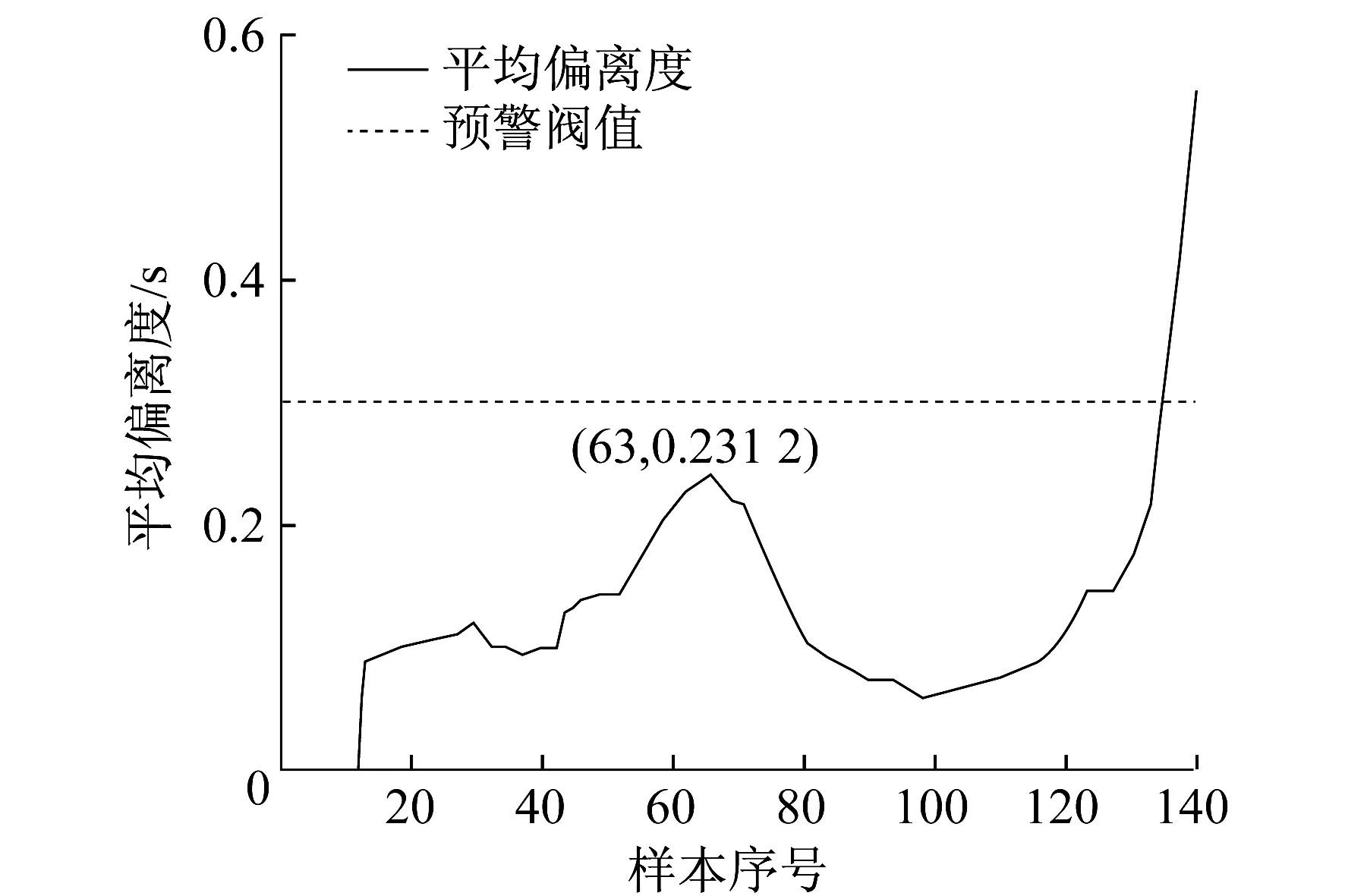
图7 平均偏离度曲线

由式(11)可知,故障预警阈值为

EAN=kEN=1.3×0.231 2=0.300 56

计算发现,在第134个数据点的平均偏离度为0.278 0,第135个数据点的平均偏离度为0.316 2。因此,预警模型会在第134个数据点和第135个数据点之间发出预警信号,相比较第140个数据点预警提前了5.4个数据点,即提前1.10 h。

5 结 语

本文利用MSET建立压气机正常运行状态下的非参数模型。引入偏离度衡量观测向量与估计向量之间的偏离程度,然后利用滑动窗口法确定故障预警阈值。实验仿真表明,该模型可以有效地进行故障预警,有一定的应用前景。