基于含噪声虚拟参考反馈的稳压器压力控制

钱 虹, 陈传奇, 张凯文

(1.上海市电站自动化技术重点实验室, 上海 200090; 2.上海电力大学, 上海 200090)

稳压器是压水堆核电站一回路系统中的重要设备之一。核反应堆正常运行时,稳压器的压力要维持在一定值[1]。若压力过高,则会损坏容器从而造成安全事故;压力过低,则满足不了电厂的经济性要求。因此,稳压器压力的稳定控制具有重要的现实意义。

国内外有许多学者对稳压器的压力控制进行了研究,目前实际运用的控制策略仍是传统PID控制,但对于时变系统的控制效果不太理想且难以满足变工况运行的控制需求。文献[2]运用PI控制器和线性二次型调节器分别对稳压器的压力进行控制并作比较,但控制效果均不太理想。文献[3]将灰色预测算法与常规PID控制相结合,设计了稳压器压力控制器,但预测精度不高。文献[4]将虚拟参考反馈整定方法运用在锅炉厂的功率控制上,但只考虑了结构较为简单的PI控制器,实用性不高。文献[5]利用模糊算法对稳压器降压系统进行在线辨识,解决了稳压器压力时变性、非线性的问题,但没有提及稳压器压力控制器的设计问题。文献[6]运用虚拟参考反馈方法对无人旋翼机模型控制器进行了设计,但未考虑模型变工况的情况。文献[7]利用虚拟参考反馈方法对工厂变工况实例进行了控制器参数辨识,但忽略了含噪声信号对输出数据的影响。

因此,本文提出了一种闭环含噪声干扰的虚拟参考反馈整定(Noise-containing Virtual Reference Feedback Tuning,NVRFT)方法,消除了噪声干扰对于系统输出的影响以及实际变工况运行对控制器造成的影响,具有更好的控制性能和抗干扰能力。

1 稳压器压力模型

常规压水堆采用饱和蒸汽稳压方式,即通过电加热和喷淋实现压力控制。基本方法是:通过加热器加热稳压器中的水,水汽化后使压力升高;通过喷淋阀喷入一回路温度较低的冷却剂,部分蒸汽冷凝使压力降低。

常规压水堆核电站稳压器是对核电厂一回路压力进行控制的重要设备。稳压器压力系统是非自衡系统,具有时变性。考虑到稳压器压力系统模型的复杂性,通常可将模型的喷淋阀开度改变量和稳压器压力改变量的差分方程形式[8]表示为

y(k)+a1(k)y(k-1)+a2(k)y(k-2)=

b0(k)u(k)+b1(k)u(k-1)+

b2(k)u(k-2)

(1)

式中:y(k)——系统输出,即按照一定时序的稳压器压力的变量;

k——时刻;

ai(k),bj(k)——模型时变参数,i=1,2,j=0,1,2;

u(k)——系统输入,即按照一定时序的喷淋阀开度变量。

由于在不同的喷淋阀开度下稳压器的压力呈现非线性变化[9],故为了实现在不同的喷淋阀开度变量下的良好控制特性,就必须克服变工况引起的变系数的影响。目前,压水堆核电站的稳压器压力控制大多采用传统的PID控制器,难以满足变工况运行下的控制需求。

2 闭环含噪声虚拟参考反馈整定方法的原理及实现

2.1 虚拟参考反馈整定方法

假设稳压器的压力模型为P(z-1),压力控制系统的控制器为C(θ;z-1),那么稳压器压力控制系统的方框图如图1所示。其中:θ为控制器参数向量;r(k)为参考信号,e(k)为偏差信号。

图1 稳压器压力控制系统方框图

在实际生产中,稳压器压力系统的数学模型难以建立,即P(z-1)是未知的。此时,可运用虚拟参考反馈整定(Virtual Reference Feedback Tuning,VRFT)方法对系统的输入数据u(k)和输出数据y(k)(k=1,2,3,…,N,N为数据长度)进行运算,求得性能指标,再对控制器参数进行辨识。VRFT的系统方框图如图2所示,虚线方框内均为虚拟信号,用于计算机内部计算。

图2 VRFT的系统方框图

该方法引入了一个虚拟参考信号r1(k),满足

r1(k)=y(k)M-1(z-1)

(2)

式中:M-1(z-1)——参考模型。

那么虚拟参考信号经控制器得到的输出为

u1(k)=C(θ;z-1)[M-1(z-1)-1)y(k)]

(3)

根据式(3)中的u1(k)与稳压器降压系统的输入数据u(k),采用最小二乘法得出VRFT方法的性能指标J(θ)为

(4)

选取合适的滤波器L(z-1)对数据进行滤波[10],即

L(z-1)=[1-M-1(z-1)]M-1(z-1)

(5)

那么,

(6)

式中:uL(k)——被控对象输入数据滤波后的数据;

yL(k)——被控对象输出数据滤波后的数据;

eL(k)——偏差信号经滤波得到的信号。

则式(4)可转换为

(7)

其中

φL(k)=β(z-1)L(z-1)·

[M-1(z-1)-1]y(k)

(8)

(9)

式中:β(z-1)——控制器的参数化形式。

此时,转换后的性能指标只与压力系统的输入数据和输出数据有关,而与被控系统的数学模型无关。

在变工况运行条件下,为提高控制器的适应性,采用递推最小二乘法在线辨识得到最优控制器参数为

(10)

式中:KP(k)——比例调节系数;

KI(k)——积分调节系数;

KD(k)——微分调节系数。

2.2 基于NVRFT方法的去噪方法

VRFT方法是假设压力系统的输出数据中不包含噪声信号的干扰,但在实际运行工况下,稳压器加热元件套管与底封头连接焊缝、压力组件输出不可忽略的脉冲干扰以及稳压器内部组件的老化等都会对传感器的测量数据产生干扰,从而形成噪声。因此,去噪过程是达到精准控制的前提。含噪声信号干扰的闭环系统方框图如图3所示。

图3 含噪声干扰的闭环系统方框图

若根据含有噪声信号的被控对象输出数据,采用VRFT方法就必定会得到一个有偏的控制器参数向量,导致实际控制性能恶化。因此,可利用辅助变量的方法来克服噪声干扰所带来的影响。辅助变量ζ(k)的选择,必须满足如下两个条件:

(11)

(12)

式中:E——数学期望;

d(k)——噪声干扰。

其中:

ζ(k)=β(z-1)L(z-1)[M-1(z-1)-1]y1(k)

(13)

(14)

最后得到的辅助变量ζ(k)为

ζ(k)=β(z-1)L(z-1)[M-1(z-1)-1]y1(k)

(15)

则式(7)可转换为

ζ(k)C(θ;z-1)eL(k))2

(16)

相应地,式(10)可转换为

(17)

3 仿真分析

运用MATLAB/Simulink仿真平台,对基于NVRFT方法的核电站稳压器压力控制系统进行仿真验证,仿真模型如图4所示。图4中,输入和输出数据分别为喷淋阀开度的改变量和稳压器压力的改变量,即前文中的u(k)和y(k)。

图4 基于NVRFT方法的稳压器压力控制和PID控制的仿真模型

此外,选取高斯白噪声作为干扰d(k),其均值为零,方差为1;PID控制中的被控对象传递函数采用的是文献[5]所辨识的90%满功率(Full-power,FP)工况与80%FP工况下的稳压器降压模型;NVRFT方法设计的控制器参数的初值为θ0=[0.257,-0.45,0.218]。

3.1 NVRFT方法的可行性验证

本文选用的参考模型为

(18)

采样时间为0.1 s。参考模型与闭环系统的频率响应曲线如图5所示。

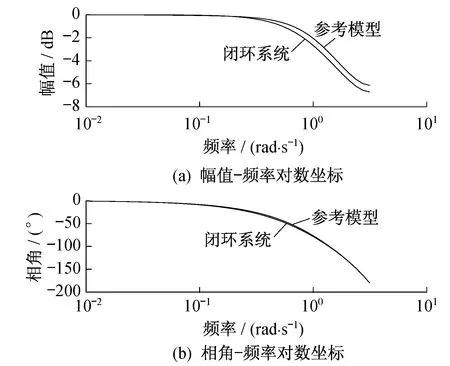
图5 参考模型与闭环系统的频域响应曲线

由图5可知,参考模型的频率特性与闭环系统的频率特性基本一致,证明了NVRFT方法的可行性。

3.2 抗干扰性验证

考虑噪声信号的干扰,对VRFT方法和NVRFT方法的去噪效果进行对比,结果如图6所示。

图6 NVRFT方法与VRFT方法的去噪效果对比

由图6可知:直接使用VRFT方法处理含有噪声信号的输出数据时,响应曲线出现大量毛刺,不利于系统稳定;而利用NVRFT方法得到的响应曲线比较稳定,去噪效果明显。

3.3 基于NVRFT方法的控制效果

给定控制回路一个1 MPa的阶跃输入,观察NVRFT方法和传统PID控制方法对核电站稳压器压力控制的效果。其中,传统PID控制方法的控制器参数是由Z-N方法与试凑法相结合得出的,其中KP=0.5,KI=0.5,KD=0,仿真结果如图7所示。其中,当t<200 s时,两种控制方法的性能指标数据如表1所示。

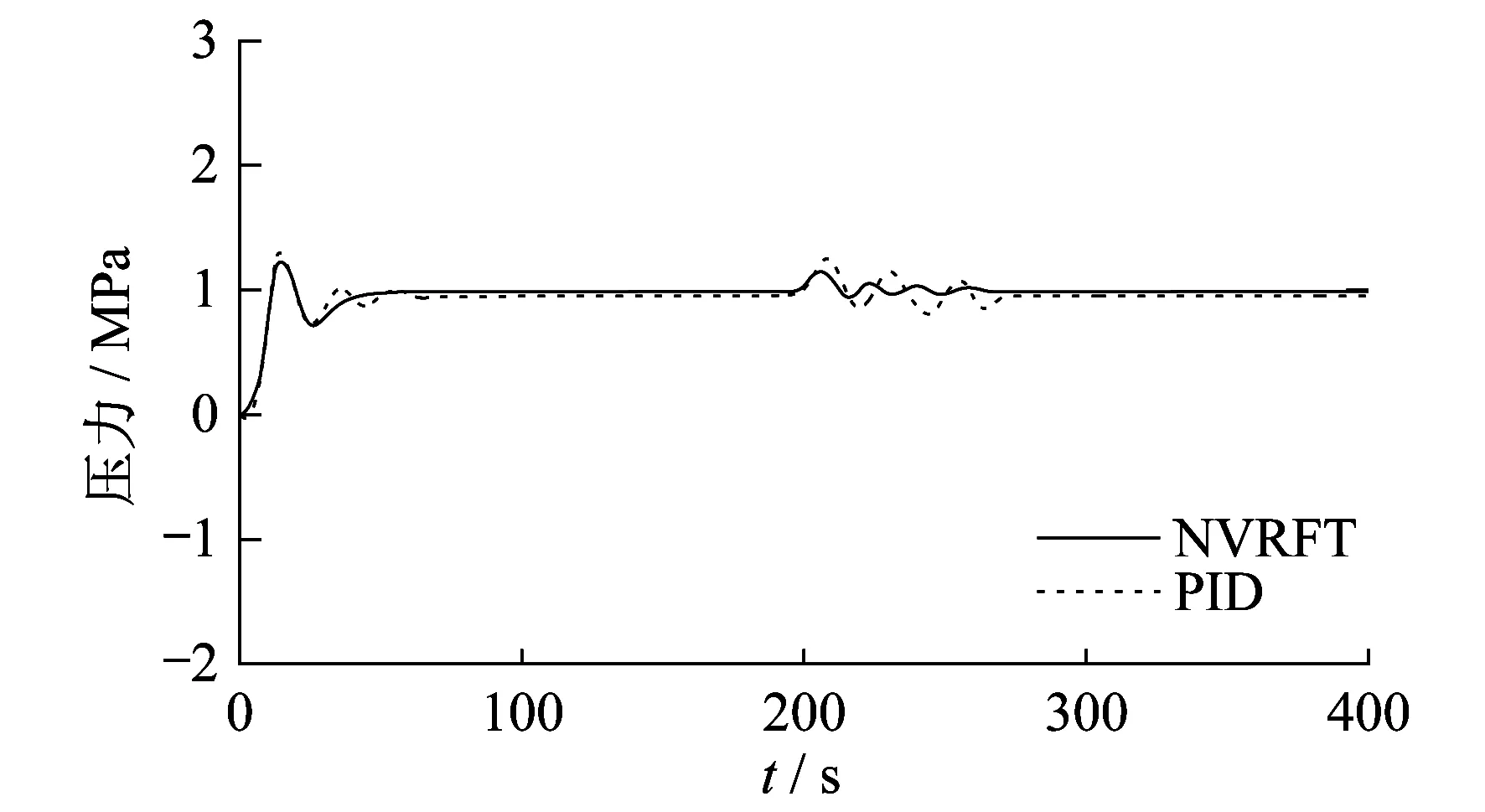
图7 NVRFT方法与PID方法响应曲线对比

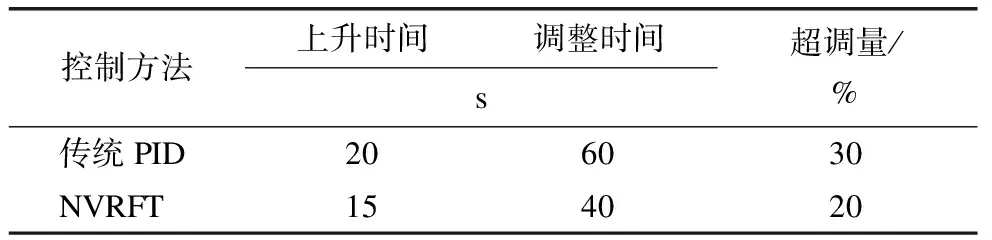
表1 性能指标数据对照表

由图7和表1可知:当t<200 s,即压力系统为单工况运行时,NVRFT方法的上升时间减少了33%,调整时间减少了50%,超调量减少了50%,表明NVRFT方法在增强系统稳定性的同时,调节速度也在加快;当t=200 s时,即降压系统变工况时,NVRFT方法能够比传统PID方法更加快速地回到稳定状态。

通过仿真结果可得:在选择合适的参考模型以逼近闭环系统的特性后,NVRFT方法具有较强的自适应能力和抗干扰能力,能够很好地应对核电站稳压器压力系统的非线性、时变性,以及噪声信号对输出数据产生干扰的特点。

4 结 语

针对核电站稳压器压力系统非线性、时变性且实际运行中受到噪声信号干扰的特点,本文提出了一种NVRFT方法,利用辅助变量法改进了VRFT的性能指标,从而消除了噪声信号的影响。该方法运用递推最小二乘算法在线辨识控制器的控制参数,在不需了解被控对象特性的情况下,间接解决了被控对象时变性与非线性的问题。仿真结果表明:该方法有利于弥补传统PID方法的控制局限性,较传统PID控制方法具有更好的控制效果、自适应能力和抗干扰能力。但文中暂未讨论稳压器压力与水位的耦合关系,有待进一步的完善和研究。