基于LSTM模型的SCR系统喷氨量串级预测控制

周 硕, 钱玉良, 王 丹

(上海电力大学 自动化工程学院, 上海 200090)

选择性催化还原脱硝技术(Selective Catalyytic Reduction,SCR)是利用还原剂氨气降低氮氧化物(NOx)含量的一种工艺,而还原反应与机组负荷、含氧量、温度和氨气量等相关。目前,喷氨量控制方式有两种:一种是固定氨氮摩尔比去除氮氧化物[1];另一种是固定浓度目标值,利用实际值与目标值的偏差,修正摩尔比,实现对浓度的控制。然而时变系统严重影响了传统PID控制的控制性能[2]。管亚鑫[3]分析了SCR脱硝系统延时原因,将Smith预估控制器加入到控制系统中,解决了大时滞的问题。秦天牧等人[4]选择多尺度核偏最小二乘法建立脱硝系统模型,并利用多向核偏最小二乘(Multiway Kernel Partial Least Squares,MKPLS)算法和预测控制方法对SCR脱硝系统进行优化控制,取得了良好的控制效果。卜平凡等人[5]研究并仿真了动态矩阵控制在控制系统中的有效性。

本文充分考虑了时变系统对预测控制的影响,基于滚动预测思想,在长短期记忆(Long Short-Term Memory,LSTM)神经网络输入层叠加前一时刻输出,深入学习数据的深层特征,持续在线更新参数;以系统模型为基础,构建喷氨量预测控制系统;采用串级控制的系统架构,给出基于LSTM模型的SCR系统喷氨量串级预测控制方法,在LSTM预测控制系统中串联一个PID控制器,内环PID控制克服小扰动,外环预测控制快速及时跟踪设定值。

1 基于LSTM的SCR系统NOx浓度预测模型

LSTM网络因其内部拥有独特的门结构机制,能够提取并共享长期时序数据的特征,并具有对NOx排放量的长期记忆功能。通过LSTM网络构建出口NOx预测模型,并引入滚动预测方式,实现了模型的自我微调,提高了预测准确率。

1.1 LSTM网络

LSTM网络是对循环神经网络(Recurrent Neural Network,RNN)的一种改良,利用其特殊结构解决了因使用RNN而引起的梯度消失、爆炸等问题。对于应用到LSTM的时序x={x1,x2,x3,…,xn},隐层记忆单元具有记忆前一时刻状态的功能,并通过定向连接通道将该信息传给当前神经元,输入层与隐含层共同完成输入特征的提取,并且通过权值与时间序列建立数学联系,即

h(t)=φ(Ux(t)+Wh(t-1)+b)

(1)

式中:h(t),h(t-1)——隐含层在t时刻和t-1时刻的输出;

φ(·)——激活函数;

U——t时刻输入层与隐含层间的权重;

W——(t-1)时刻与t时刻隐含层之间的权重;

x(t)——输入层t时刻的输入;

b——偏置量。

LSTM网络通过门结构增加或减少记忆单元的状态信息,有效地利用长期时序数据。LSTM网络隐含层内部模块结构如图1所示。隐含层增加自连接的存储和门结构,使LSTM网络具有读取、写入和判断功能。

图1 LSTM网络隐含层内部模块结构

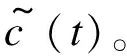
i(t)=σ(Wxix(t-1)+Whih(t-1)+

Wcic(t-1)+bi)

(2)

Whch(t-1)+bc)

(3)

式中:σ(·)——Sigmoid激活函数;

Wxi,Whi,Wci——输入门的权重矩阵;

c(t-1)——t-1时刻记忆单元状态;

bi——输入门偏置量;

tanh(·)——双曲正切函数;

Wxc,Whc——候选值的权重;

bc——候选值偏置量。

f(t)=σ(Wxfx(t-1)+Whfh(t-1)+

Wcfc(t-1)+bf)

(4)

(5)

式中:Wxf,Whf,Wcf——遗忘门的权重矩阵;

bf——遗忘门偏置量。

输出门控制当前神经元的输出信息o(t),并与单元状态信息值c(t)共同决定细胞在下一时刻向隐含层传递的单元状态信息h(t)。隐含层的输出为一维列向量,经线性回归即得到处理后NOx浓度的预测值。输出门更新计算如下

o(t)=σ(Wxox(t-1)+Whoh(t-1)+

Wcoc(t-1)+bo)

(6)

(7)

式中:Wxo,Who,Wco——输出门的权重矩阵;

bo——输出门偏置量。

LSTM网络通过综合灵活利用门结构,控制信息在隐含层内外传递,使得梯度持续流动,并随着时间递进动态修改循环权重,使得LSTM网络能够学习时间跨度较大的依赖关系[6-9]。

1.2 滚动预测方法

锅炉燃烧是一个动态过程,导致脱硝系统具有不确定性,NOx排放的动态时序数据存储在分布控制系统中,历史条件影响着现状[10]。基于历史数据的NOx浓度预测实质上是构建一个模型来反映未来NOx浓度与历史数据、时间和其他参数之间的映射关系。这种关系随时间等因素而变化,因此需要提供相对完整的信息才能准确地描述。根据系统特性,本文提出一种滚动预测的方法,其时序逻辑如图2所示。该方法使网络在实际应用中能够持续学习,通过自我微调来改变性能,从而提高模型的预测质量。

图2 滚动预测的时序逻辑

滚动预测将网络接收到的最新数据与上一时刻的预测结果共同形成训练数据,重新训练权重,不断寻找最佳权重。LSTM网络从t2时刻起自动更新模型参数,通过追踪参数变化规律来提高预测质量,可快速应用于不同SCR系统和模型失配的情况。

2 基于喷氨量的预测控制算法

基于SCR系统模型预测出口NOx浓度,预测控制将未来的参考信息纳入控制问题,在每个时间步骤都进行在线优化,是将运算结果驱动到参考值的最佳控制操作,改善了控制器的性能[11]。神经网络预测控制首先要全面感知系统的运行状态,即

y(t)=g[y(t-1),…,y(t-n),x(t-d),…,

x(t-d-m)]+v(t)

(8)

式中:y(t)——t时刻系统的输出;

n——历史时间步长;

v(t)——t时刻系统干扰;

d,m——时滞时间。

则t+k时刻,神经网络输出预测值为

ym(t+k)=fNN[y(t),…,y(t-n+1);

x(t+k-d),…,

x(t+k-d-m);P]

(9)

式中:k——预测步长,k≥d;

P——模型参数。

以上文的LSTM网络为基础,利用持续的新样本更新预测模型,实现准确预测未来时刻出口NOx浓度随工况和操作变量的变化趋势。

在控制系统中,模型的预测输出与系统实际输出存在偏差。为了防止仅依靠已建立模型的开环控制引起误差,在计算k+1时刻优化控制量前,将输出实际值y(k)与预测值ym(k)之间的偏差,通过反馈校正补偿到k时刻的预测输出,使模型预测近似于对象输出。反馈校正后的输出值为

yp(k+1)=ym(k+1)+y(k)-ym(k)

(10)

滚动优化是依据SCR脱硝系统目标函数的约束要求,确定未来时刻的控制量{u(k+i-1),i=1,2,3,…,M},M为控制长度。通过最小化预测值与设定值之间的误差,确保系统输出NOx浓度保持在规定的范围内。通过解决以下问题来确定控制量

u(k+i-1)]2

(11)

s.t.u∈[umin,umax]

式中:mi,ni——误差权重和控制权重;

yr——期望的输出序列;

u(k)——k时刻氨气流量控制量;

N——预测长度;

umax,umin——喷氨量范围的上下限。

为了延长氨气阀门的使用寿命,在目标函数J(k)中对喷氨量的变化进行约束,以确保在满足目标期望的同时减小控制量的变化,减少阀门调整次数,对阀门起到一定程度的保护作用。可将控制长度M内的每个控制变量视为需要由目标函数计算的自由变量,因此控制长度越小,计算量越小。选择控制长度的经验法则是将其设置为预测长度的10%～20%。预测长度的整定原则是使样本涵盖开环瞬态系统响应。误差权重确定原则是使SCR系统设定值与输出值的误差达到最小。控制权重表示目标函数受控制量变化的影响,用于约束控制增量。当ni较小时,使系统响应时间减小,控制增量变化较大。

3 基于LSTM模型的SCR系统喷氨量串级预测控制策略及实现过程

基于上述LSTM建模方法和预测控制算法,本文给出了一种基于LSTM模型的SCR系统喷氨量串级预测控制方案。为处理非线性和不确定性,应用LSTM辨识系统模型,利用滚动预测方式,实现对SCR系统出口NOx浓度状态实时性的全面感知;以SCR系统模型为基础,建立基于LSTM的串级预测控制系统,融合出口NOx浓度设定值,滚动优化计算氨气流量,并由PID副控制器计算喷氨量与反馈氨气流量之间的控制量偏差,调节氨气阀门开度。使用能得到快速响应的PID控制器,有利于克服由小扰动引起副控制器对象的偏差幅值。双层控制结构把不同的控制性能要求交予不同层去处理,解决了抗干扰与鲁棒性难以兼顾的问题[12]。具体控制策略如图3所示。

图3中,u(k)是预测控制滚动运算得到的控制量,p(k)为氨气流量反馈量,w(k)为实际喷氨量,y(k)为系统实际输出。由副控制器给定输入u(k)与氨气流量反馈量p(k)构成控制误差为

e1(k)=u(k)-p(k)

(12)

利用PID控制系数Kp,Ti,Td与控制误差的线性组合,计算氨气控制量,并控制氨气调节阀门。控制律为

(13)

式中:T0——采样间隔时间。

基于LSTM模型的串级预测控制既保留PID控制抗干扰能力强的特性,又利用预测控制实时预测和智能响应的优点;LSTM通过门结构的配合使网络具有记忆能力,能较好地跟踪时间序列动态变化。利用LSTM滚动预测算法构建出口NOx浓度预测模型,并将LSTM算法与预测控制相结合,提高算法精度,能够快速适应不确定系统。基于LSTM模型的串级预测控制实现过程如下:

(1)设置控制和预测步长M,N;

(2)基于NOx浓度目标值得到预期目标序列,即参考轨迹yr(k+j)(j=k,k+1,k+2,…,Ny),Ny为时间序列范围上限;

(3)以SCR系统对象的输入输出数据作为训练样本对LSTM模型进行训练;

(4)将某段时序数据作为输入变量输入到LSTM预测控制模型中,得到预测值ym(k+1)和实际输出y(k+1);

(5)依据式(10),利用预测偏差在线修正模型预测,误差序列为e2(k+j)=yr(k+j)-yp(k+j)(j=k,k+1,k+2,…,Ny);

(6)由式(11),根据目标函数对控制量u迭代求解,得到作为PID副控制器输入的最优解u(k+j);

(7)由式(12)和式(13)计算控制误差e1(k+j)和控制律w(k+j);

(8)设k=k+1,返回步骤1。

4 仿真结果比较

4.1 预测仿真

以电厂脱硝工艺的先验知识为理论基础,选择800组总煤量、总风量、进口含氧量、入口NOx浓度和前一时刻出口NOx浓度值的实际数据作为LSTM模型的输入。为了减小输入参数差异对模型性能及过拟合概率的影响,归一化处理样本数据,将前400组数据作为训练集数据,其余400组作为测试集数据,验证预测效果。

在训练过程中通过损失函数LSTM模型的输出误差,使用优化算法寻找误差最小值,更新模型权重,最终获得收敛的LSTM模型。测试集数据通过确定好的收敛模型得到出口NOx浓度预测值,并利用损失函数调整更新模型参数,以确保模型预测的准确性。网络结构参数由多次试验得到,具体见表1。

表1 结构参数

将测试集数据应用到LSTM模型、径向基函数(Radical Basis Function,RBF)模型和反向传播(Back Propagation,BP)神经网络模型中,将预测结果与实际出口NOx浓度进行比较。图4为测试集数据在不同模型中的预测结果。

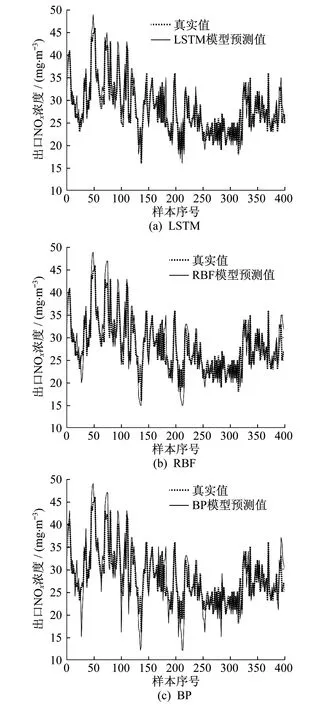
图4 不同模型预测结果对比

采用均方根误差(Root Mean Square Error,RMSE)和平均绝对误差(Mean Absolute Percentage Error,MAPE)来验证模型精度,仿真结果如表2所示。

表2 不同建模方法比较

从工程实践来看,在用足够多样本建模时,MAPE小于10%,表明该模型可以反映对象的真实动态。通过表2可以发现,LSTM模型的MAPE小于3%,RMSE小于1.5 mg/m3,能较好地表达模型映射关系,滚动预测明显地减小了预测的偏差,增强了模型的适应能力,网络的预测精度满足预测控制算法的设计要求。

4.2 控制仿真

根据国家规定的排放要求,设定SCR系统出口NOx浓度为50 mg/m3,分别采用PID串级控制以及基于LSTM模型的串级预测控制,实现对SCR系统喷氨量最优化控制,仿真结果如图5～图7所示。

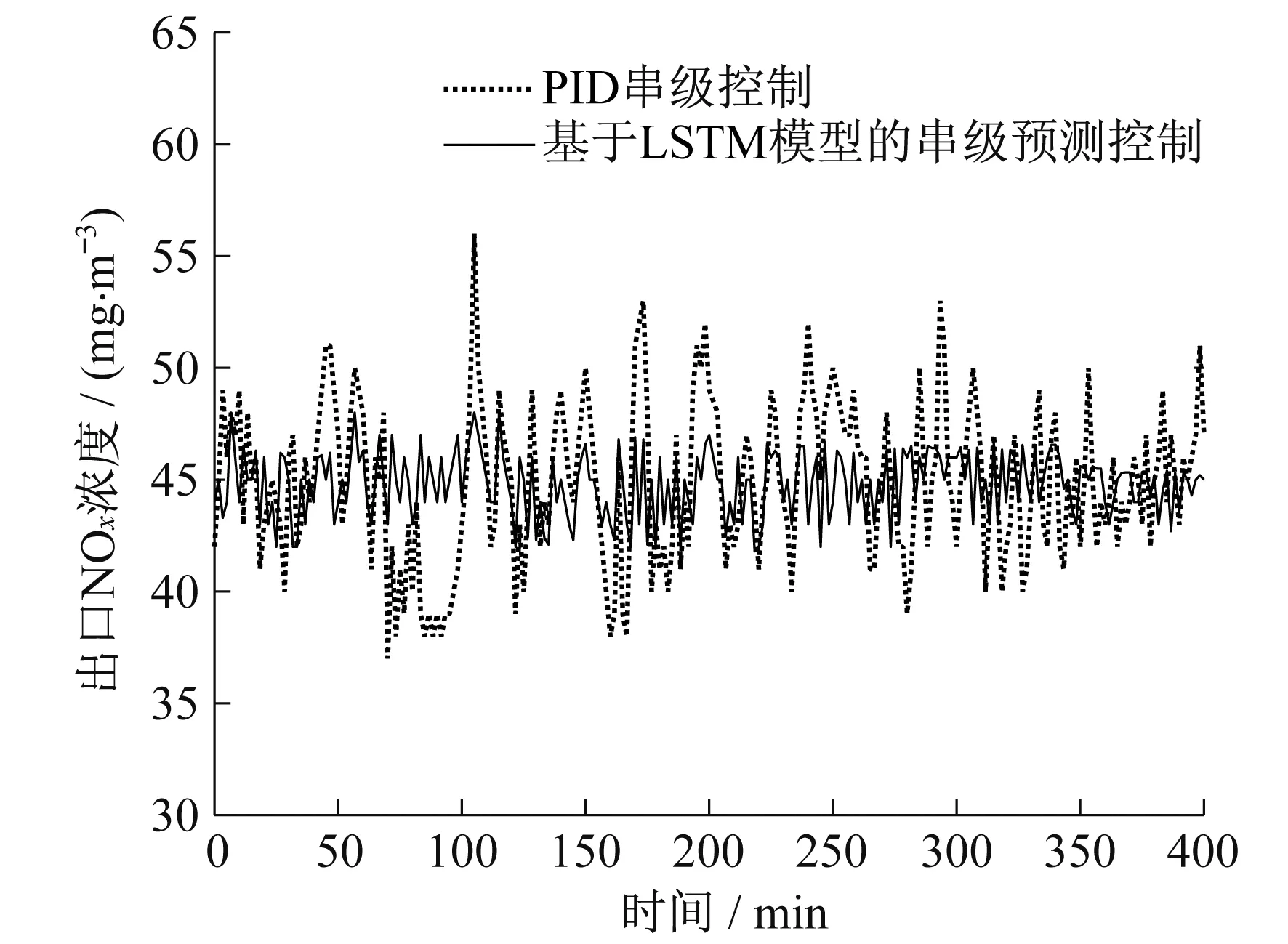
图5 出口NOx浓度控制仿真结果

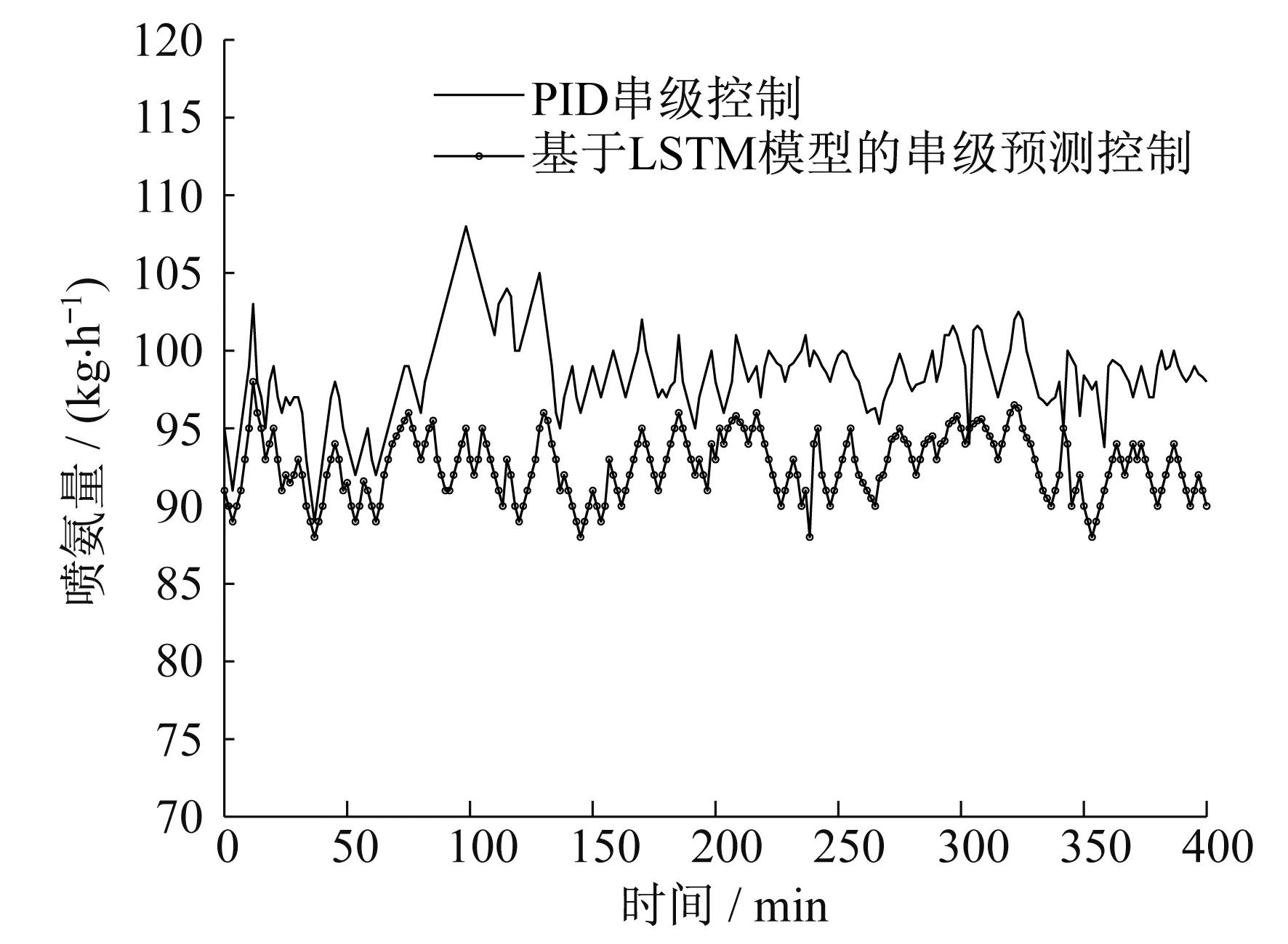
图6 喷氨量控制仿真结果

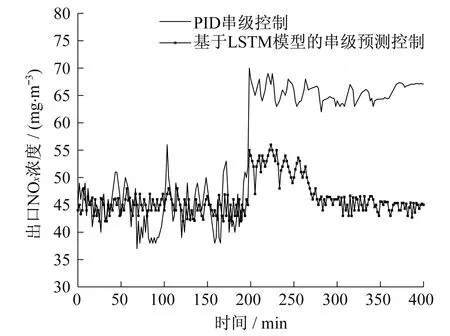
图7 机组变化导致模型失配对比的仿真结果

由图5和图6可知:基于LSTM模型的串级预测控制使SCR系统出口NOx浓度基本均低于设定目标值,稳定在45 mg/m3,出口浓度标准差为1.446 2 mg/m3,最长调节时间为8.6 min;PID串级控制的喷氨量曲线始终在基于LSTM模型的串级预测控制曲线之上,其出口NOx浓度标准差为3.478 2 mg/m3,平均喷氨量为98.425 3 kg/h,最长调节时间为18.8 min。相比之下,基于LSTM模型的串级预测控制不断对喷氨量进行优化,及时跟踪入口NOx浓度变化,控制精度更高,使喷氨量基本稳定在95 kg/h,平均喷氨量为92.586 7 kg/h。

图7表明,模型在200 min后处于不匹配的状况,PID串级控制的出口NOx浓度超出国家要求,并持续失去控制作用,无法恢复到原有控制效果。基于LSTM模型的串级预测控制实现氨气供需的实时匹配和智能响应,与PID串级控制相比,出口浓度在200 min后一段时间的波动较小,并将其稳定在设定值,展示出了基于LSTM模型的串级预测控制在模型失配时优越的控制性能。

5 结 语

本文将LSTM滚动预测应用于SCR脱硝优化系统中,建立了基于LSTM的SCR系统模型。采用LSTM预测控制策略,通过滚动计算找到最佳控制量。将LSTM预测控制与PID控制相结合,最终建立喷氨量的串级预测控制系统。仿真结果表明,基于滚动预测的LSTM算法建立的SCR系统模型精度要明显好于RNN算法和BP算法。建立的基于LSTM模型的串级预测控制系统相比于传统PID串级控制获得较高的烟气净化率和较低的喷氨量,使出口NOx浓度接近设定目标值,提高了SCR系统安全经济运行的质量水平。