基于掩护面积的弹炮结合防空武器系统优化配置

杨志宏，王凤山，郭子曜

(陆军工程大学野战工程学院，江苏 南京 210007)

0 引言

弹炮结合防空武器系统综合了自行高炮机动灵活和便携式导弹打击精准之优势，是机场、港口、指挥所等战场关键目标对空防护的重要力量，其优化配置问题是以作战效能为评估导向和指挥决策的重点问题[1-2]。文献[3]运用解析几何方法，建立了以最佳距离和掩护扇区为指标的防空武器阵地配置模型，但掩护区域理想化、简单化。文献[4]建立了以“最少数量”完成射击任务的模糊线性规划火力分配模型，得出区域防空各型防空武器梯次部署最佳配置比，适用于大规模整体防空优化配置研究。文献[5]以掩护角最大为优化目标，建立了海上编队区域防空舰艇配置距离优化模型，给出了区域防空舰艇最佳配置距离和最小配置数量范围求解方法。文献[6]针对大规模、多约束、非线性要地末端防空兵力优化部署问题，建立了基于火力覆盖能力的末端防御兵力优化部署模型。

弹炮结合防空武器系统的优化配置问题，符合武器装备效能评估的基本规则[7-9]。文献[3—6,10—12]以多类型防空武器混编部署，多目标组合优化为属性进行综合评价；但面对联合作战体系需求，战场防护目标多、区域大，一线作战力量自身防空资源有限等约束，如何优化配置有限力量发挥最佳末端防护能力，还鲜有研究。针对以上问题，以作战决策部署中最关心的掩护区域面积为特征参量，首次提出基于掩护面积的优化配置研究，通过蒙特卡洛方法求解各配置模型下的掩护面积，分析掩护面积特征，直观对比防护效能优缺点，为弹炮结合防空武器系统选择配置提供决策支持。

1 弹炮结合防空武器系统配置模型

弹炮结合防空武器系统通常以集中配置掩护重要目标，根据地形条件、战术要求和掩护目标数量及区域大小选择配置模型，常用的配置模型有圆形配置、三角形配置和矩阵配置等。圆形配置因其能有效应对方向不明等复杂情况空袭而被广泛应用，因此，重点研究圆形配置模型。圆形配置模型，即以掩护目标为中心，在部署半径CR的圆上配置1个战斗套型m辆战车，指挥车位于掩护目标附近。弹炮结合防空武器系统圆形配置主要包括圆形均匀配置、圆形非均匀配置和圆形主从配置。

以1个战斗套型6辆弹炮结合武器系统战车，部署半径CR=100～500 m为例，构建圆形均匀配置模型，6辆战车均匀配置在部署半径的圆上，相邻战车间距相等，如图1所示。

区别于圆形均匀配置，圆形非均匀配置是在部署半径CR的圆上非均匀配置6辆战车，相邻战车间距不均匀(D≥100 m)，其部署特征是重点方向战车数量多，战车相对密集，次要方向战车数量少，战车间距大，如图2所示。

相异于圆形均匀配置和非均匀配置，圆形主从配置是以1辆战车为基准，其余5辆战车均匀配置在部署半径CR的圆上，基准战车和指挥车位于掩护目标附近，如图3所示。其部署特征是配置模型左右对称，外围相邻战车分布均匀，相对于圆形均匀配置，外围战车间距增大。

图1 圆形均匀配置Fig.1 Circular uniform configuration

图2 圆形非均匀配置Fig.2 Circular non-uniform configuration

图3 圆形主从配置Fig.3 Circular master slave configuration

2 圆形配置掩护面积及求解方法

2.1 掩护面积描述

单个弹炮结合防空武器的火力防区由防空导弹和高炮共同决定。防空导弹和高炮的火力有一定的重叠，将其火力防区划分为防空导弹攻击区、弹炮火力重叠区和高炮攻击区三部分[8]。随机假设弹炮结合防空武器的导弹系统有效斜射距离452～5 500 m，有效高度63～3 800 m，高低射角0°～76°；高炮系统有效斜射距离2 800 m，有效射高2 100 m，高低射角-5°～86°。其火力防区图如图4所示。

图4 火力防区划分示意图Fig.4 Schematic diagram of fire power defense area division

因此，单个弹炮结合防空武器掩护区域可以看作是以防空武器为中心，以有效射击斜距离为半径的概略半球体。定义有效射击空间范围在地面的投影为掩护区域面积[13]，形状为圆形，大小用面积表示。

1个战斗套型弹炮结合防空武器系统圆形配置模型下，单战车导弹系统和高炮系统射击死界可被其他战车掩护区域覆盖，因此，忽略单战车射击死界。1个战斗套型弹炮结合防空武器(导弹系统或高炮系统)掩护区域在地面投影面积，如图5所示，图中白点为战车配置位置。同时，因弹炮结合防空武器导弹系统与高炮系统仅在射击斜距离上有所差异，因此，导弹和高炮系统掩护区域面积特征具有相似性，在面积描述和计算上具有一致性。

图5 1个战斗套型掩护区域示意图Fig.5 Schematic diagram of cover area of combat unit

为便于下一步计算和分析掩护面积及其特征，将掩护面积分为累积型和分布型。其中，i辆战车以上火力(含)可重叠掩护区域面积为累积型掩护面积；有且只有i辆战车火力可重叠掩护区域面积，为分布型掩护面积。

2.2 累积型掩护面积

以Si表示第i辆战车的掩护区域在地面的投影面积。集合S={S1,S2，…，Si，…，Sm}表示1个战斗套型弹炮结合防空武器系统m辆战车掩护面积的集合，则存在不同数量战车的火力重叠掩护区，即Si∩Sj∩…∩Sk(i≠j≠k,1≤i,j,k≤m)，m为战车的总数。其中，战斗火力掩护重叠性最强为S*，即：

S*=S1∩S2∩…∩Si∩…∩Sm

(1)

式(1)中，S*表示m辆战车重叠掩护面积。

(2)

(3)

显然，fβ(1)=100%，理论上，fβ(1)≥fβ(2)≥…≥fβ(m)。

2.3 分布型掩护面积

(4)

(5)

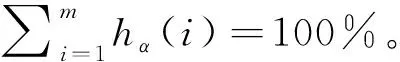
2.4 掩护面积计算数学模型及方法

蒙特卡洛方法是一种以统计抽样理论为基础，通过随机变量的统计抽样检验或随机模拟，估计求解问题近似解的一种数值计算方法[14]。

如图6所示，蒙特卡洛方法计算弹炮结合防空武器系统掩护面积的基本原理是向矩形区域Sfull均匀撒入P个随机点，其中，Pin个点落入掩护区域S内部，其余点落入掩护区域之外，当P→∞时，存在以下的关系：

(6)

式(6)中，S为弹炮结合防空武器战车重叠掩护区域面积，Sfull为重叠区域所在矩形区域面积。因此，掩护区域面积为：

(7)

1个战斗套型弹炮结合防空武器系统掩护区域由多个大小不同、重叠层数不同的区域组成，同时，受配置半径和相邻战车间距约束，弹炮结合防空武器掩护面积数学模型为：

(8)

式(8)中，S为1个战斗套型弹炮结合防空武器系统掩护面积；m为交叉重叠的层数，即战车数量；n表示同为i层的区域个数；Xj_max为i层第j块区域横坐标上限，Xj_min为i层第j块区域横坐标下限；Yj_max为i层第j块区域纵坐标上限，Yj_min为i层第j块区域纵坐标下限；CR为配置半径；D为相邻战车间距。

图6 防空武器掩护重叠区域随机布点图Fig.6 A random layout of overlapping area coverd by air defense weapon

2.5 计算步骤

通过式(7)、式(8)可知，为提高弹炮结合防空武器系统掩护面积的计算精度，可缩小掩护区域所在矩形区域，增加撒入点数量。

为全面分析弹炮结合防空武器系统掩护区域交叉重叠的相异性，按照由内向外，重叠层数由多到少逐层逐个求解掩护面积，如图7所示。推理计算包括7个步骤：

步骤1基于配置模型确定战车配置位置，绘制掩护区域示意图和特征图；

随着年龄增长，自然老化或光老化都会造成皮肤生物黄色素的堆积，其中年龄与脂褐素含量的关系早有报道[20]。随着年龄增长，脂褐素会在人体细胞内逐渐沉积，不仅影响皮肤颜色，而且能够通过挤占细胞空间位置，影响细胞正常功能。随着年龄增长，对脂褐素的清除能力降低，进一步造成脂褐素沉积。

步骤2计算并标记掩护区域相交点坐标信息；

步骤3由内向外确定掩护区域交叉重叠掩护的层数及其相关的战车，并确定相同层数区域的个数n；

步骤4利用解析法求得相同层每块区域外边沿坐标上限和下限，即Xj_max,Xj_min,Yj_max,Yj_min；

步骤5利用Matlab中rand函数随机生成P=106个在[Xj_min、Xj_max]、[Yj_min、Yj_max]之间的坐标，如果坐标在相关武器掩护区域内，Pin计数1次；反之，不计数，求出i层掩护面积：

步骤6重复步骤3、步骤4、步骤5，直至求解所有区域面积；

步骤7求得总面积：

图7 基于蒙特卡洛方法的求解流程图Fig.7 A flow chart of solution based on Monte Carlo menthod

3 掩护面积仿真计算及结果分析

3.1 圆形均匀配置掩护面积

圆形均匀配置时，以弹炮结合防空武器系统部署半径CR=300 m，相邻战车间距D=CR为例。绘制弹炮结合防空武器导弹系统掩护区域示意图(高炮系统掩护区域示意图与其相似)，如图8所示。

图8 圆形均匀配置掩护区域示意图Fig.8 Schematic diagram of circular uniform covre area

为便于观察掩护区域特征，部署半径不变，适当缩小战车射击斜距离，取射击斜距离为900 m。绘制弹炮结合防空武器系统掩护区域特征图，如图9所示。可清晰显示掩护区域特征：掩护区域均匀对称，重叠层数相同区域面积大小相等。

图9 圆形均匀配置掩护区域特征图Fig.9 Feature diagram of circular uniform covre area

表1 圆形均匀配置分布型掩护面积Tab.1 The distributed cover area of circular uniform configuration

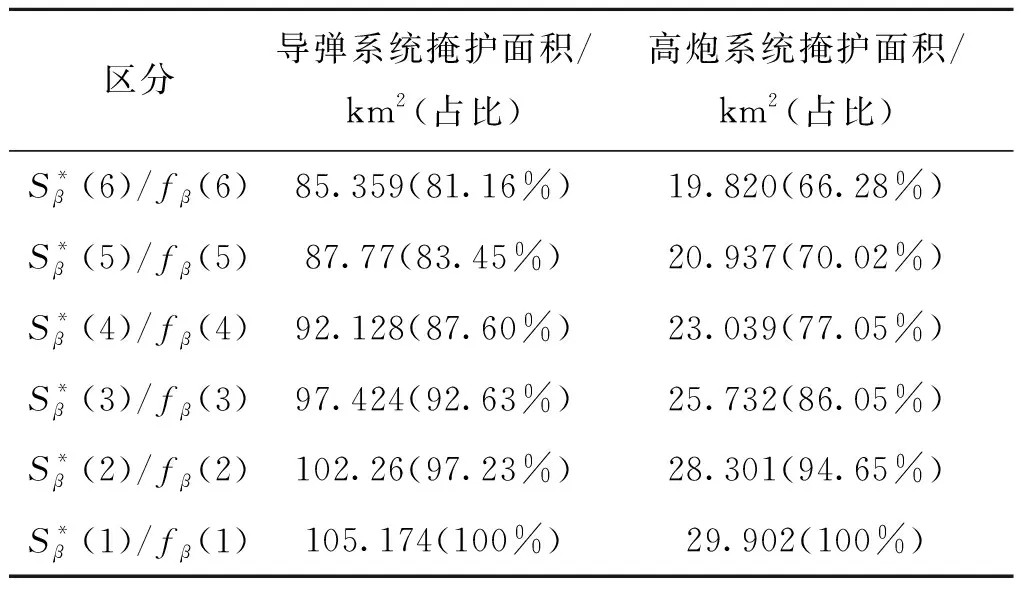
表2 圆形均匀配置累积型掩护面积Tab.2 The accumulated cover area of circular uniform configuration

3.2 圆形非均匀配置掩护面积

圆形非均匀配置时，设部署半径CR=300 m，战车在部署半径CR的圆上非均匀配置，相邻战车间距D≥100 m。为使计算结果具有普遍性和代表性，在部署半径CR=300 m，相邻战车间距不小于100 m的约束下，随机确定6辆战车部署位置，绘制弹炮结合防空武器系统掩护区域示意图，如图10所示。

图10 圆形非均匀配置掩护区域示意图Fig.10 Schematic diagram of circular non-uniform covre area

对比均匀配置和非均匀配置掩护面积示意图，较难看出掩护区域差异性。因此，缩小射击斜距离，取射击斜距离为900 m，绘制弹炮结合防空武器系统掩护面积特征图，如图11所示。可清晰显示掩护区域特征：掩护区域相同层的区域面积大小均不相等。

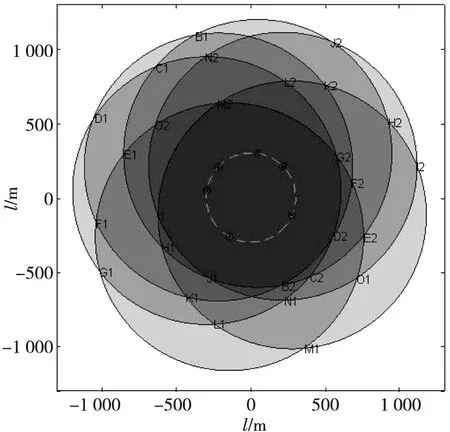
图11 圆形非均匀配置掩护区域特征图Fig.11 Feature diagram of circular non-uniform covre area

表3 圆形非均匀配置分布型掩护面积Tab.3 The distributed cover area of Circularnon-uniform configuration

表4 圆形非均匀配置累积型掩护面积Tab.4 The accumulated cover area of circularnon-uniform configuration

3.3 圆形主从配置掩护面积

圆形主从配置时，部署半径CR=300 m，绘制弹炮结合防空武器导弹系统掩护区域示意图(高炮系统掩护区域示意图与其相似)，如图12所示。

图12 圆形主从配置掩护区域示意图Fig.12 Schematic diagram of circular master-slave configuration covre area

同理，为便于观察掩护区域特征，缩小射击斜距离，取射击斜距离为900 m，绘制弹炮结合防空武器系统圆形主从配置掩护区域特征图，如图13所示，可清晰显示掩护区域特征：掩护区域左右对称，相同层数区域面积左右相等。

图13 圆形主从配置掩护区域特征图Fig.13 Feature diagram of circular master-slave configuration covre area

表5 圆形主从配置分布型掩护面积Tab.5 The distributed cover areaof circular master-slave configuration

3.4 结果分析

理论上，弹炮结合防空武器系统圆形配置时，部署半径越大掩护面积越大；相邻战车间距越大，掩护面积越大；战车均匀分布时掩护面积比非均匀分布时掩护面积大，即配置模型越规则掩护面积越大。从计算结果看，弹炮结合防空武器系统圆形配置三种配置模型下的掩护面积，主从配置(113.31 km2，33.77 km2)>均匀配置(105.173 km2，29.902 km2)>非均匀配置(102.747 km2，29.221 km2)，与理论分析一致，相互印证了理论与结果的正确性。

表6 圆形主从配置累积型掩护面积Tab.6 The accumulated cover area of circular master-slave configuration

对比圆形配置三种配置模型下的核心掩护区域面积，非均匀配置[85.509 km2(83.22%)，19.902 km2(68.11%)]>均匀配置[85.359 km2(81.16%)，19.820 km2(66.28%)]>主从配置[85.067 km2(75.07%)，19.678 km2(58.28%)]，由此可得，非均匀配置能够形成较为密集火力，利于重点防护。同时，对比圆形配置三种配置模型下的掩护面积的特征图，圆形均匀配置、主从掩护区域分布均匀对称，能够构成全方位火力拦截，但火力较为分散。

4 结论

本文首次提出了基于掩护面积的弹炮结合防空武器系统优化配置研究，一定程度上解决了有限防空资源优化配置发挥最佳防护效能问题。定义的累积型、分布型掩护面积，利于分析火力掩护区域特征，基于蒙特卡洛方法的掩护面积计算推理规则机，可相对准确计算掩护面积，进而直观对比防护效能。仿真计算结果表明，圆形配置模型下，配置模型越规则掩护面积越均匀且面积越大，但核心区域面积越小，利于全方位拦截但不利于重点防护，反之，配置模型越不规则掩护面积越不均匀且面积相对较小，但核心区域面积较大，利于重点防护。在军事实践中，应根据实际情况恰当选择配置模型。