孔隙缺陷对三维编织C/C复合材料等效弹性性能的影响
魏坤龙,史宏斌,李 江,唐 敏
(1.西北工业大学航天学院,陕西西安 710072;2.西安航天动力技术研究所燃烧、热结构与内流场重点实验室,陕西西安 710025;3.航天动力技术研究院,陕西西安 710025)
1 前 言
三维编织C/C复合材料因其具有耐烧蚀、抗分层以及高温下强度保持率高等优点,广泛应用于固体火箭发动机喷管、高速飞行器翼前缘、导弹端头帽和军用飞机等领域[1-2]。弹性性能是工程材料结构设计的重要参数,可以用来预测材料受到外部载荷作用时的力学响应。三维编织C/C复合材料在制备、加工和使用过程中,不可避免会产生大量孔隙、微裂纹等缺陷,这些缺陷尤其是孔隙缺陷对三维编织C/C 复合材料的力学性能带来很大影响[3],孔隙缺陷的出现会劣化材料性能,使得材料弹性模量降低。因此,研究孔隙缺陷对三维编织C/C复合材料弹性性能的影响,对于材料结构的精细化设计和工艺优化具有重要意义。
目前,关于含孔隙缺陷的三维编织复合材料弹性性能的研究已经有文献报道。早期,梁军等[4]利用Eshelby和Mori-Tanaka理论推导了三维编织复合材料基体含有特定形状微裂纹的弹性性能预报方法。燕瑛等[5]通过刚度体积平均法,分析了平面编织单层板材料基体中的孔隙率对材料弹性模量的影响。Zeng T 等[6]利用数学均匀化方法,研究了基体含有特定形状裂纹的三维编织复合材料的弹性模量。近年来,采用代表性体积单胞模型结合有限元方法成为研究复合材料力学性能的有效手段,任明法等[7]采用代表性体积单胞模型预测了基体含孔隙的复合材料单层板的弹性常数。卢子兴[8]等采用单胞模型研究了平纹机织复合材料的力学性能,在单胞有限元网格中引入“零刚度”单元模拟孔隙缺陷,模拟结果与实验结果相符。石多奇等[9]、Shen等[10]采用单胞模型和“零刚度”单元计算了基体孔隙率对二维和三维编织陶瓷基材料等效弹性性能的影响。徐焜等[11]研究了孔隙随机分布对三维编织复合材料弹性性能的影响,采取弱化纤维束性能的方法考虑了纤维束孔隙的影响,忽略了纤维束材料的非均质性。齐泽文等[12]采用通用单胞模型建立了纤维束单胞模型,进一步考虑了纤维束孔隙对三维四向编织复合材料弹性性能的影响。然而,上述研究主要是针对三维编织复合材料,考虑了基体和纤维束孔隙缺陷对材料弹性性能的影响,没有考虑纤维束/基体界面缺陷的影响。与树脂基复合材料不同,三维编织C/C复合材料在制备过程由于纤维和基体之间热膨胀失配,在纤维束/基体界面会产生大量孔洞和脱层,这些界面缺陷对三维编织C/C复合材料力学性能的影响需要进一步考虑。
因此,本研究通过三维编织C/C复合材料微结构扫描电镜显微观测,将三维编织C/C复合材料视为由纤维增强相、基体相和界面相组成,考虑了纤维增强相、基体相和界面相孔隙缺陷,建立了孔隙缺陷随机分布的纤维丝尺度和纤维束尺度的双尺度单胞模型,基于渐进均匀化方法和周期性边界条件,预报了含孔隙缺陷的三维编织C/C复合材料等效弹性性能,并由此研究了纤维增强相、基体相和界面相孔隙率对三维编织C/C复合材料等效弹性性能的影响。
2 考虑孔隙缺陷的双尺度单胞模型
2.1 三维编织C/C复合材料及其显微形貌
图1为本文研究的三维编织C/C 复合材料编织结构示意图和实物照片,其轴向(Z向)使用由树脂和纤维拉挤成型的刚性碳棒形成增强结构,径向(R 向)采用软纤维束在轴向增强网络之间编织,轴向纤维束呈正三角形排列,径向纤维束呈0°、60°和120°方式围绕轴向纤维束排布,通过沥青浸渍、炭化增密工艺向纤维预制体中引入基体碳,最后经过高温石墨化工艺获得高密度C/C复合材料。图2为三维编织C/C 复合材料扫描电镜显微形貌,由图可见,三维编织C/C 复合材料内部含有大量孔洞、微裂纹等缺陷,孔洞的形状、大小和分布呈不规则状,具有随机性特点,其中基体孔洞较多且孔径较大。图3为纤维束/基体界面局部显微形貌,可见纤维束和基体之间存在明显的界面层,厚度约20μm,周围存在未被基体填满的孔洞,纤维束内部也含有许多微孔隙。
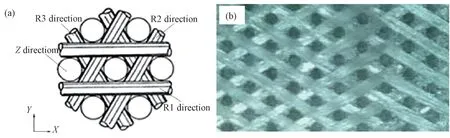
图1 三维编织C/C复合材料 (a)编织结构;(b)材料实物Fig.1 3D braided C/C composites (a)braided structure;(b)specimen
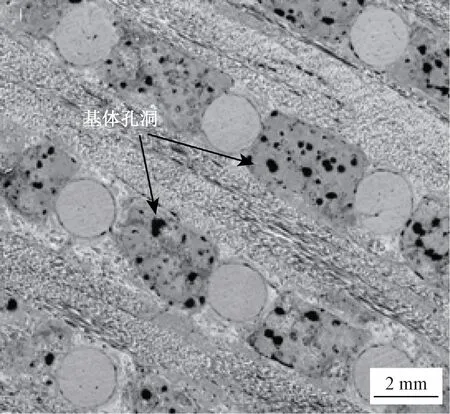
图2 三维编织C/C复合材料的扫描电镜照片Fig.2 SEM photograph of the 3D braided C/C composites

图3 三维编织C/C复合材料界面层的扫描电镜照片Fig.3 SEM photograph of interface between fiber bundle and matrix
2.2 纤维丝尺度单胞模型
根据第2.1节所述,三维编织C/C复合材料孔隙缺陷主要分布在三个区域:纤维束内部、纤维束/基体界面层和基体内部,纤维束内部孔隙主要是由于纤维丝浸渍基体不完全产生的,为了较为真实反映材料内部不同部位的孔隙缺陷,需要建立纤维丝尺度的单胞模型和纤维束尺度的单胞模型。
纤维束一般由数千根纤维丝平行排列而成,在材料制备过程中,纤维丝之间被沥青碳填充,假设纤维束中纤维丝截面为圆形、纤维丝呈周期性规则排列、纤维丝满足横观各向同性、基体为各向同性,建立轴向纤维束和径向纤维束纤维丝尺度的单胞有限元模型,如图4所示,其中轴向纤维束单胞尺寸为8.4μm×8.4μm×8.4μm,纤维含量为80%,径向纤维束单胞尺寸为9.96μm×9.96μm×9.96μm,纤维含量为57%,对单胞模型进行有限元网格离散,共划分网格单元分别为43680个和43725个。

图4 纤维丝尺度单胞有限元模型 (a)轴向纤维束;(b)径向纤维束Fig.4 Unit cell models for fiber bundles (a)axial fiber bundle;(b)radial fiber bundle
2.3 纤维束尺度的单胞模型
根据材料编织方式的周期性,建立纤维束尺度的单胞模型,如图5所示,其单胞可看作是由通过四根纤维棒中心,包含三层纤维束的长方体构成。单胞模型包括纤维增强相、基体相和界面相,单胞尺寸为5.54 mm×3.2 mm×3.3 mm,界面相厚度为20μm。建模过程中将轴向纤维束截面近似为圆形,径向纤维束截面形状近似为矩形,并假设纤维束空间走向为直线,不同方向纤维束/基体界面相厚度均匀一致,选取六面体单元和少量四面体单元对单胞进行网格离散,纤维相单元与界面相单元、界面相单元与基体相单元之间共节点连接,共划分网格单元80900个。

图5 三维编织C/C复合材料单胞有限元模型(a.单胞b.纤维增强相c.界面相)Fig.5 Unit cell FEM model of the 3D braided C/C composites(a.Unit cell b.reinforcement c.interface)
2.4 随机孔隙缺陷分布模型
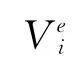
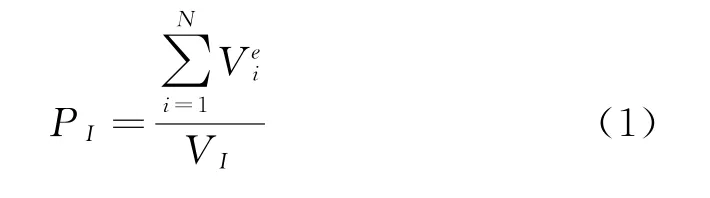
3 等效弹性性能预报方法
3.1 渐进均匀化方法[13]
对于具有周期性微结构的复合材料单胞模型,其等效弹性性能的均匀化控制方程为:
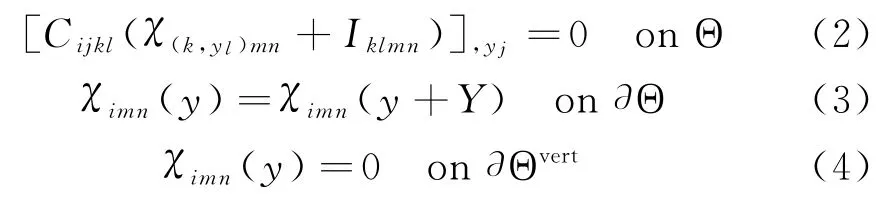
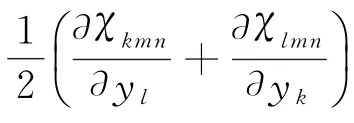
单胞等效刚度的均匀化系数可表示为:
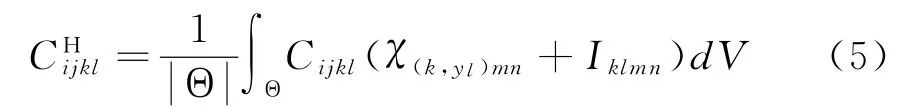
获得单胞等效刚度矩阵[CH],然后将其求逆[C]-1,进而获得材料柔度矩阵[S],最后利用柔度和工程弹性常数之间的关系,导出材料等效工程弹性常数。
3.2 周期性边界条件
采用均匀化方法计算单胞等效刚度时需要满足周期性边界条件,即单胞变形前后边界处位移要满足式(3)和式(4),通过在单胞六个自由面、边以及角的网格节点上建立相互之间的位移约束方程来实现。为了便于施加周期边界条件,要保持单胞的六个自由面上的网格节点一一对应,通过 ABAQUS 自编脚本(ABAQUS scripting)程序实现多点耦合约束方程(MPC equations)的施加。图6为单胞周期性变形示意图,变形前后单胞自由边界上任意两个距离为单胞尺度Y 的点p与q处的特征位移χ(y)相等。
3.3 等效弹性性能预报流程
采取两步均匀化流程,首先对图4所示纤维束单胞有限元模型施加周期性边界条件,引入纤维丝和基体性能,采用渐进均匀化方法计算得到轴向和径向纤维束等效弹性性能,然后将计算得到的纤维束等效弹性性能代入图5所示三维编织C/C 复合材料单胞模型中,并施加周期性边界条件,再次采用渐进均匀化方法进行计算得到材料整体等效弹性常数。
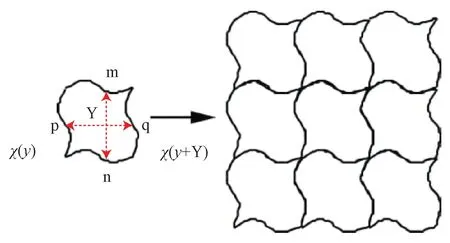
图6 单胞的周期性边界条件Fig.6 Periodic boundary condition for unit cell
4 实验内容
数值计算所需的T300纤维丝和碳基体在2500℃高温石墨化处理后的弹性性能见表1。材料拉伸实验在INSTRON5500型材料试验机上进行,如图7(a)所示,实验环境温度为(296±2)K,设计的单轴拉伸试样如图7(b),试样按照美军标MIL-HDBK-17 复合材料手册中关于碳纤维增强复合材料力学性能的测试要求设计。考虑到纤维束的模量要远大于基体碳的模量,而试件与外载荷垂直的截面内的碳纤维束呈周期性排布,为了获得更为准确的性能测试参数,试样横截面内纤维束在宽度和厚度方向均为整数根,并严格保证纤维束贯穿整个试样且平行于实验中心线,纵向变形用引伸计进行测定,横向粘贴应变片以测定泊松比,最大加载力为25 k N,加载速度为0.5 mm/min。剪切性能测试选用短梁剪切方法进行,采用Iosipescu剪切测定材料的剪切模量,通过在试样表面±45°方向贴应变片以测定ε+45°和ε-45°,工程剪切应变即为γ=ε+45°-ε-45°。Iosipescu剪切试样的V 型切槽角度为110°,剪切应力通过剪切破坏载荷除以剪切区域的横截面积得到,剪切模量通过剪切应力与应变关系计算得到。

表1 2500 ℃石墨化后纤维和基体性能[14]Table 1 Properties of fiber and matrix after 2500 ℃graphitization process[14]
5 结果与讨论
5.1 等效弹性性能预报值与实验值的对比

图7 拉伸实验机和拉伸试样实体照片(a)INSTRON 实验机;(b)拉伸试样Fig.7 Experiment apparatus and specimen (a)INSTRON instrument;(b)tensile specimen
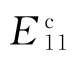

表2 纤维束等效弹性常数预报值/GPaTable 2 Predicted effective elastic constants of fiber bundles/GPa

表3 三维编织C/C复合材料等效弹性常数预报值与实验值/GPaTable 3 Predicted and experimental effective elastic constants of 3D braided C/C composites/GPa
5.2 纤维增强相孔隙率的影响
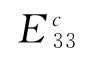
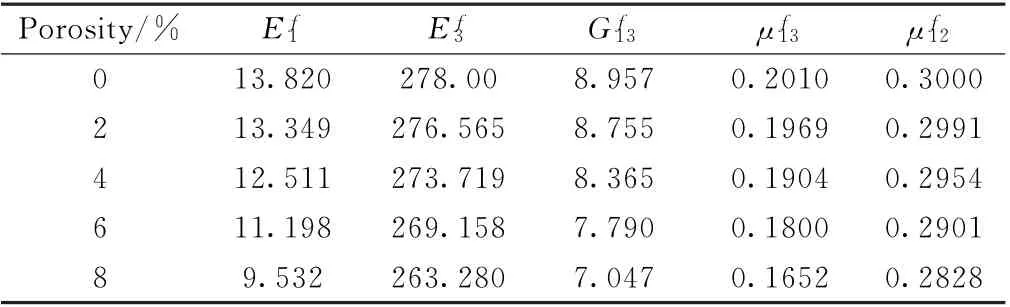
表4 不同孔隙率下轴向纤维束等效弹性常数/GPaTable 4 Predicted effective elastic constants for axial fiber bundle with porosity/GPa
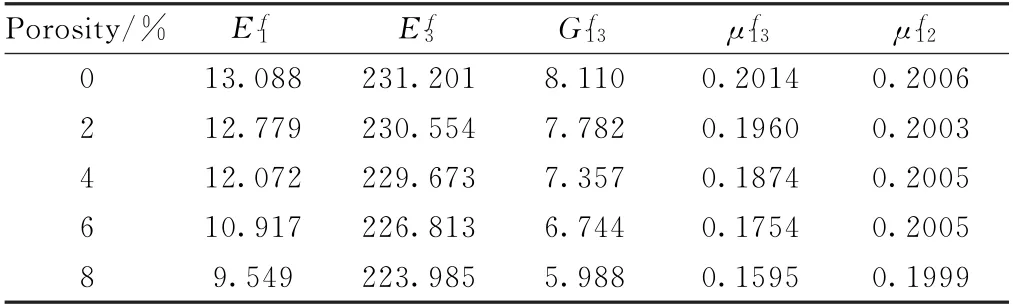
表5 不同孔隙率下径向纤维束等效弹性常数/GPaTable 5 Predicted effective elastic constants for radical fiber bundle with porosity/GPa
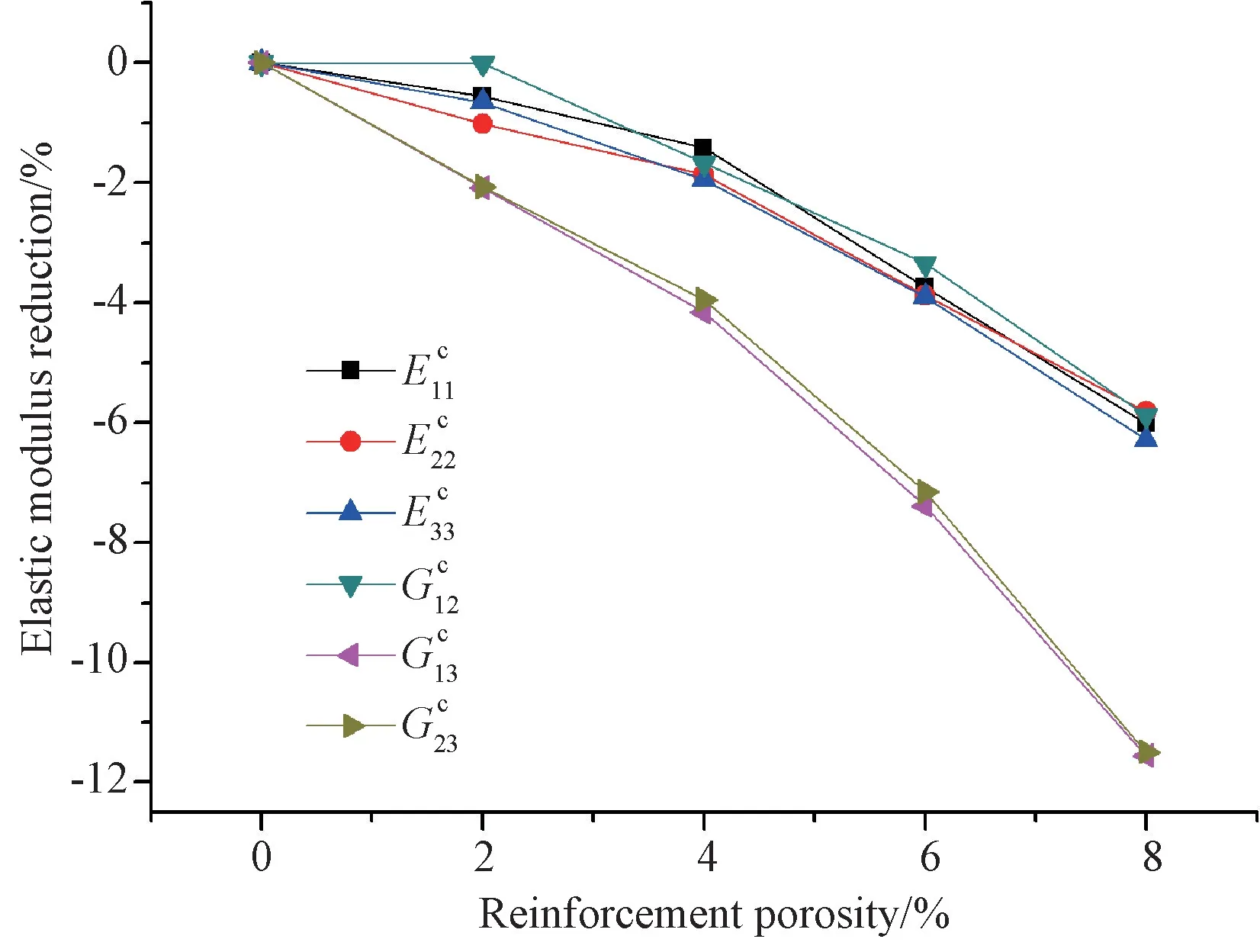
图8 纤维增强相孔隙率对C/C复合材料等效弹性模量的影响Fig.8 Effect of reinforcement porosity on the effective elastic modulus
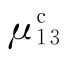
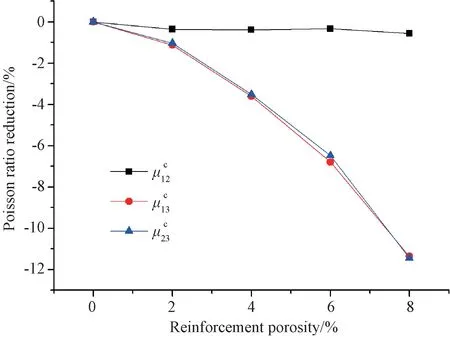
图9 纤维增强相孔隙率对C/C复合材料等效泊松比的影响Fig.9 Effect of reinforcement porosity on the effective poisson’s ratio
5.3 基体相孔隙率的影响

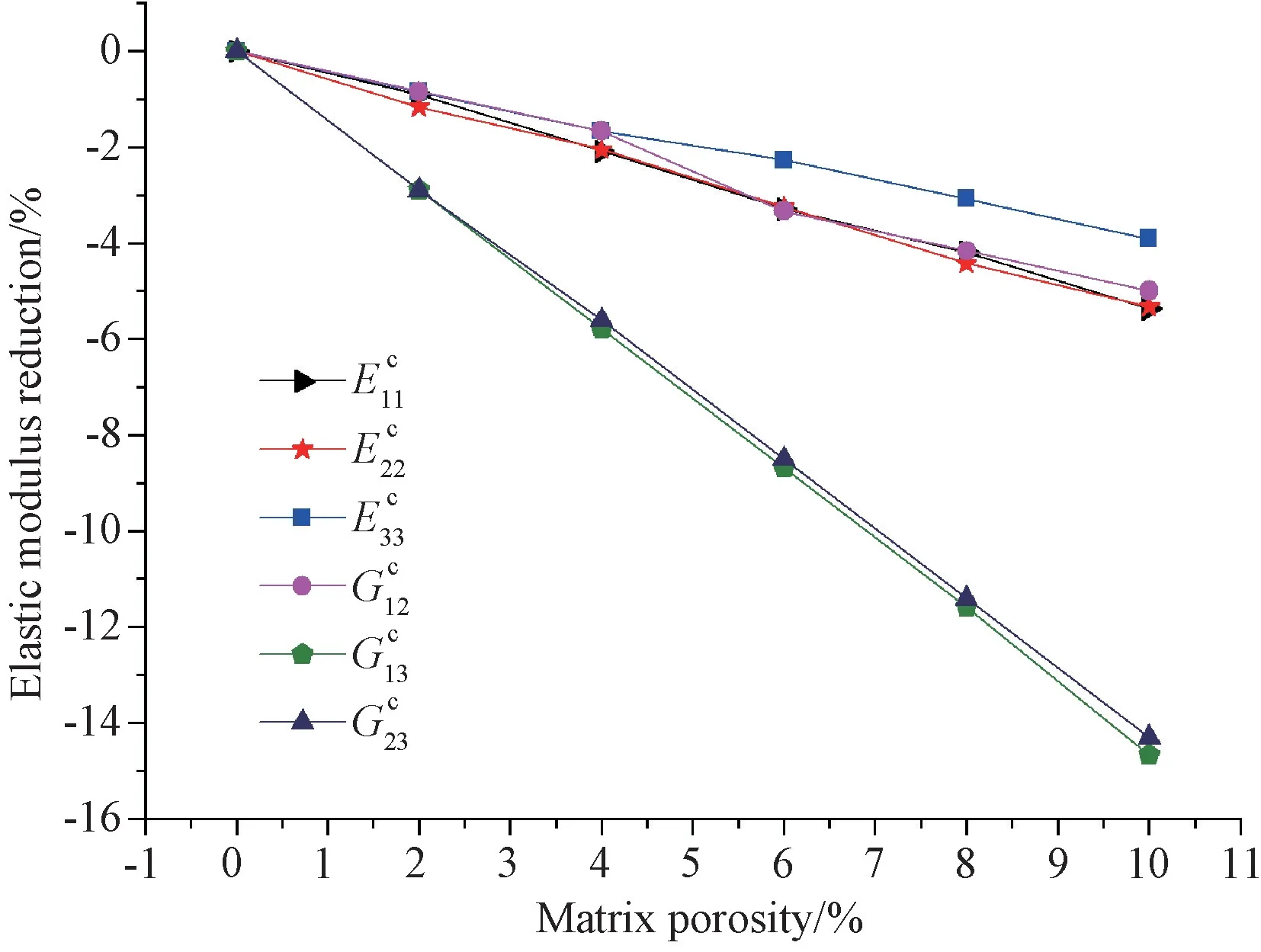
图10 基体相孔隙率对C/C复合材料等效弹性模量的影响Fig.10 Effect of matrix porosity on the effective elastic modulus


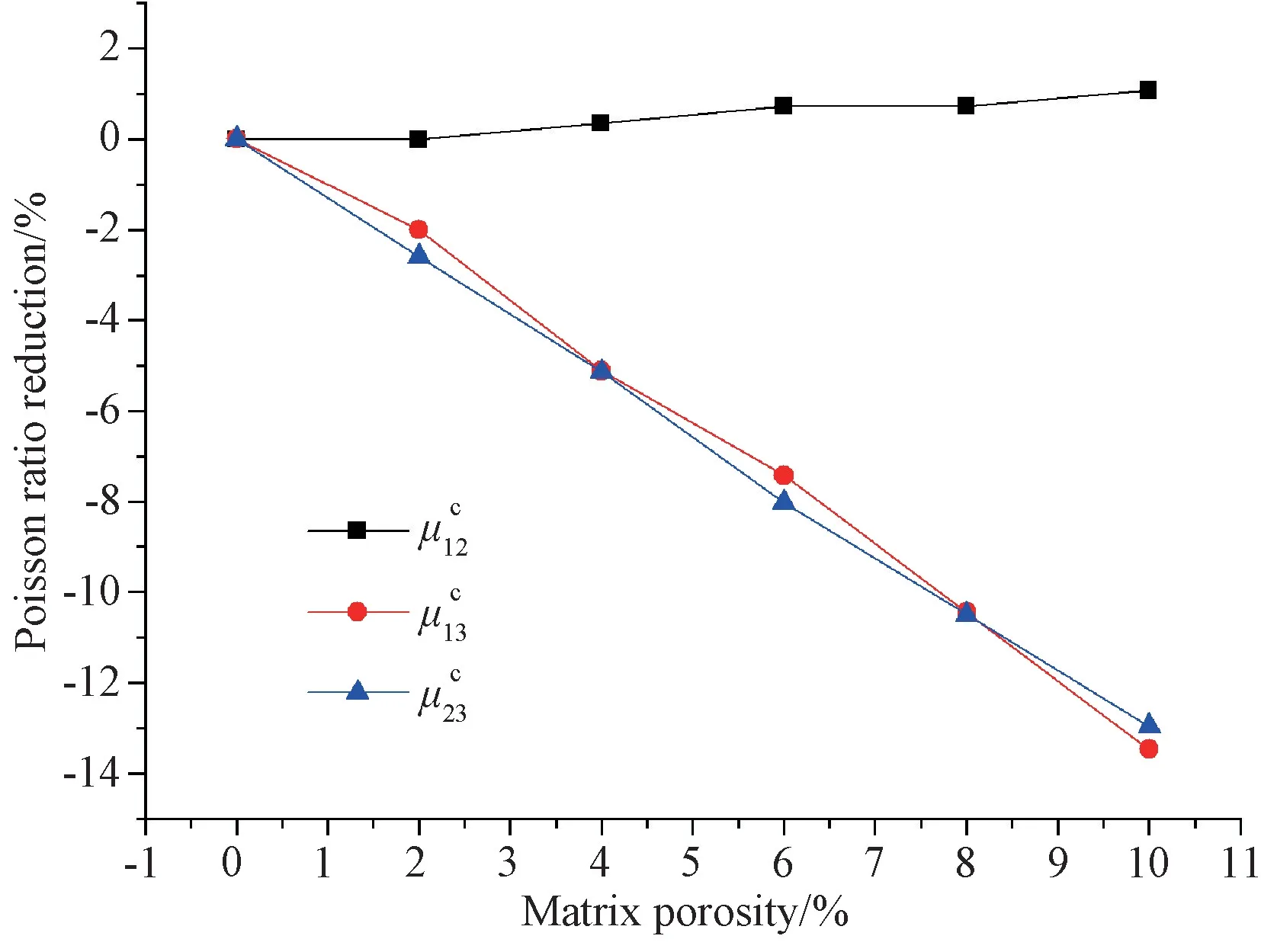
图11 基体相孔隙率对C/C复合材料等效泊松比的影响Fig.11 Effect of matrix porosity on the effective poisson’s ratio
5.4 界面相孔隙率的影响

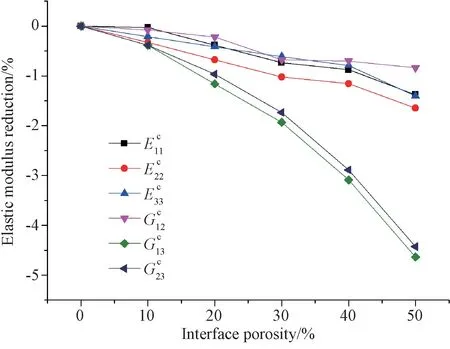
图12 界面相孔隙率对C/C复合材料弹性模量的影响Fig.11 Effect of interface porosity on the effective elastic modulus

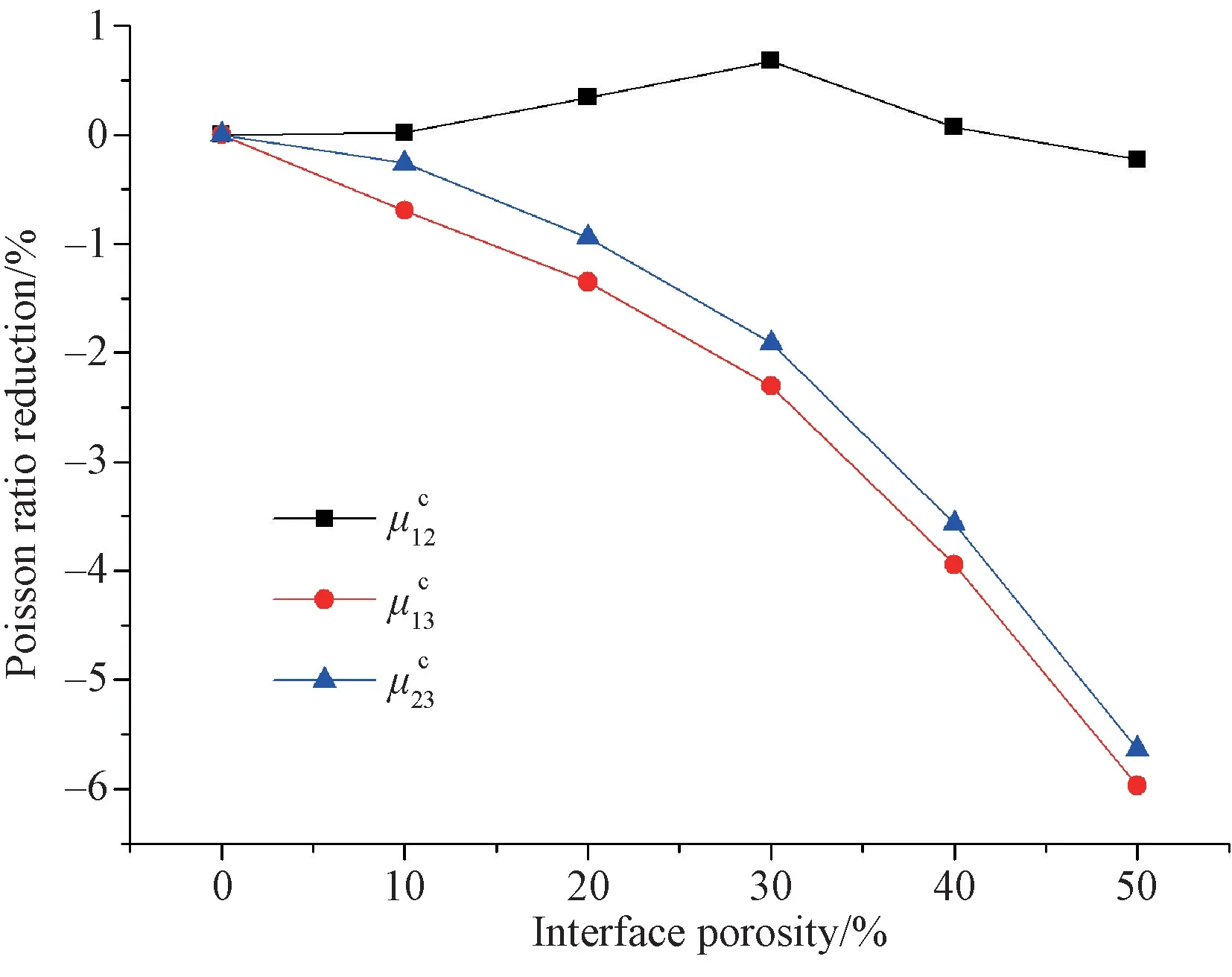
图13 界面相孔隙率对C/C复合材料等效泊松比的影响Fig.12 Effect of interface porosity on the effective poisson’s ratio
6 结 论
1.建立了考虑纤维增强相、基体相和界面相随机孔隙缺陷的三维编织C/C 复合材料等效弹性性能双尺度预报模型,通过与实测数据对比验证了双尺度预报模型的有效性,为此类材料结构精细化设计和工艺优化提供了参考;
2.随着孔隙率增加,材料弹性常数出现不同程度的递减,面外剪切模量减小幅度最大,而面内泊松比略微增大。当孔隙率为10%时,材料轴向和径向拉伸模量分别减小11.17%和12.30%,面内和面外剪切模量分别减小11.28%和29.74%,面外泊松比平均减小29.32%,面内泊松比略微增大0.26%。由于孔隙使得材料局部刚度减小,从而降低了材料的弹性模量,而不同方向弹性模量降低程度的差异使得泊松比变化规律不同;
3.基体孔隙率对材料等效弹性常数的影响总体上呈线性,纤维增强相和界面相孔隙率的影响呈非线性,各组分相的孔隙率对材料等效弹性常数的影响大小依次为:纤维增强相>基体相>界面相。由于纤维丝弹性模量大于基体,因而纤维增强相孔隙率的影响要大于基体相和界面相,而细观结构差异又导致不同组分相的影响规律各不相同。

