水分子对无定形C-S-H 凝胶微结构和力学性能的影响
马 彬,朱林伟,牛海华
(桂林电子科技大学建筑与交通工程学院,广西桂林 541004)
1 前 言
水化硅酸钙(C-S-H)是水泥基材料水化后的主要产物,对材料各项性能均有重要影响。目前,国内外学者对水泥水化过程及其相应产物结构的研究已有很多[1-3],但大多是在宏观层次上的试验和数值模拟研究,对其微观组分的结构特性和形成机制仍未有定论。
起初,通过核磁共振、扫描电镜、光谱法等[4-6]试验方法来研究C-S-H 的微观结构特性,认为C-S-H 为层状结构,且结构内部的钙硅原子比大约为1.2~2.3。由于通过已有试验方法得到的结果存在一定局限性,因此随着计算科学的发展,基于分子/原子层次的计算模拟方法无疑成为了研究材料纳米尺度结构的有效途径[7-9]。目前,通常采用Tobermorite 和Jennite类结晶体结构来研究C-S-H 的结构的特性和力学性能,但水泥水化产生的C-S-H 凝胶为无定形态,将初始晶态结构转变为无定形态结构并利用分子动力学模拟的研究成为了热点。已有的关于C-S-H 凝胶无定形态的报道多是通过高温退火或自上而下方法来实现晶态到无定形态的转变,但这些方法并不能完全体现水泥水化过程的随机性[10-11]。基于随机系统建立C-S-H 凝胶模型不仅能够体现凝胶结构的无定形态且能够满足水化过程的随机性,故本研究将采用随机系统建立CS-H 凝胶模型。
从水泥或混凝土材料的服役过程来看,水分子和C-S-H 凝胶微观结构的相互作用严重影响了材料整体力学性能和耐久性。水分子作为C-S-H 凝胶的重要组成部分,一直都是其微观结构研究的重点。Bonnaud等[12]研究了C-S-H 凝胶中的水对水泥浆体破坏过程的影响机制,并认为材料颗粒间水分子对层间粘聚力具有抑制作用,钙离子对层间粘聚力具有促进作用。Ji等[13]预测了含有五种不同水分子模型的C-S-H 模型的微观结构和弹性常数,并研究了凝胶结构内部水分子的动力学特性。郑巧等[14]研究了不同湿度下C-S-H 纳米颗粒间的相互作用,分析了湿度对材料干缩力和体积应变量的影响规律,并认为在含水量较高时材料的应力和变形受孔隙影响较大。Zehtab等[15]利用分子动力学方法研究了温度对C-S-H中不同离子和水分子扩散系数影响的规律,认为在高温下扩散系数较高。可见,目前已有文献多是针对C-S-H 结构分析和热动力学分析,少有开展水分子含量对无定形C-S-H 结构特征和力学性能影响的研究。
本研究基于随机系统建立C-S-H 凝胶无定形结构模型,利用分子动力学方法对其进行结构优化,结合径向分布函数和近邻原子数分析水分子含量对无定形C-S-H 凝胶微观结构和力学性能的影响规律。力图为水泥、混凝土等材料在干燥或高温环境下失水机制和应用提供理论指导。
2 模型建立与模拟过程
2.1 模型建立
随着水泥水化时间的增加,C-S-H 凝胶的结构逐渐接近于Jennite结构特征[16-17],其中氧化硅四面体为典型的三元重复结构。为使结构模型与实际结构更加吻合,本研究选取构成Jennite(Ca9Si6O18(OH)6·8 H2O)类结晶体结构的Ca离子、H2O 分子、OH 基团和Si3O10集团(如图1所示)作为基本单元构建无定形C-S-H 凝胶结构随机模型,其中各基本单元间的比例为9∶8∶6∶2,H2O/Si比值为1.33。

图1 C-S-H 凝胶模型的基本单元Fig.1 Basic units of C-S-H gel model
为进一步研究水分子含量对无定形C-S-H 凝胶的微观结构特征和力学性能的影响规律,确保在不同H2O/Si比值下Si原子数目为常数,分别选取H2O/Si比值为0、0.4、0.8和1.33的无定形C-S-H 凝胶结构模型为研究对象,其中水分子个数分别对应为80、48、24和0,具体基本单元数如表1所示。
2.2 模拟过程
首先,基于图1 所示的基本单元利用Materials Studio软件的Amorphous Cell模块采用随机构建的方式,建立C-S-H 凝胶体系的初始构型。根据文献[18],Ca9Si6O18(OH)6·8 H2O 无定形凝胶模型的密度设定为2.32 g/cm3,模型尺寸为19.8Å×19.8Å×19.8Å。然后,基于能量最小化综合方法(Smart minimizer)对初始构型进行几何优化,该方法的本质是组合使用最陡下降法、共轭梯度法和牛顿法对结构进行优化,确保系统能量最低。最后在系统的原子数、压力和温度均保持不变条件下对几何优化后的C-S-H凝胶模型进行分子动力学能量弛豫。从图2可见,系统的温度和势能在模拟早期波动均较大,但随着弛豫时间的增加,两者均在较小的范围内波动,表明体系趋于稳定。图3为分子动力学弛豫后的无定形结构模型,从图可见随着水分子含量的减少,模型中的硅氧四面体的聚集程度逐渐增加。
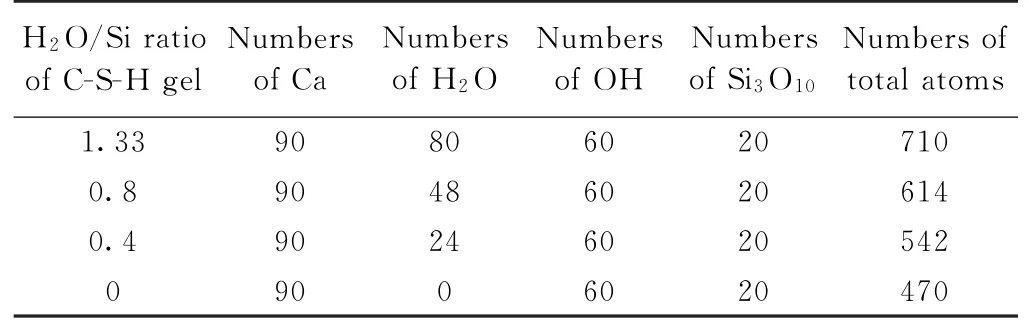
表1 不同C-S-H 模型的基本单元数Table 1 Basic units numbers of different C-S-H models

图2 分子动力学模拟过程中温度与势能的变化 (a)温度曲线;(b)势能曲线Fig.2 Changes of temperature and potential energy in process of molecular dynamics simulation(a)temperature curves;(b)potential energy curves

图3 分子动力学弛豫后的无定形结构模型 (a)H 2 O/Si=1.33;(b)H2 O/Si=0.8;(c)H2 O/Si=0.4;(d)H2 O/Si=0Fig.3 Amorphous structure models after molecular dynamics relaxation (a)H 2 O/Si=1.33;(b)H 2 O/Si=0.8;(c)H 2 O/Si=0.4;(d)H 2 O/Si=0
力场的选取决定着整个分子动力学模拟过程的准确性,鉴于C-S-H 凝胶体系为金属氧化物和非金属氧化物组成的混合体系,基本单元间的相互作用多为广义的无机共价键,故本研究采用可以精确计算众多分子及聚合物间共价和非共价作用力的Compass 力场[19]。在上述分子动力学模拟过程中为避免由于温度较高或不稳定引起热激活效应的复杂影响,系统温度控制在300 K,并采用Nose-Hoover方法进行等温调节[20],压力设定为1×10-4GPa。为保证体系达到能量最低的平衡状态,设定模拟过程的总弛豫时间100 ps,时间步长1 fs,模拟步数1×105。此外,分子动力学运动方程采用Verlet算法进行积分。
3 结果分析与讨论
3.1 径向分布函数分析
径向分布函数又称之为对关联函数是描述粒子系统中参考粒子附近粒子密度的一种方法[21],其物理意义为体系局域内的原子密度与体系平均密度之比,具体表达式为:

其中,d N 为与参考原子距离为r 到r+δr 的区域范围内的原子数,ρ 为体系的平均密度,δr 为区域距离。体系结构的差异会导致径向分布函数的取值和趋势不同,进而判断体系的状态。具有有序结构的晶体,其径向分布函数在近程和远程均有波峰出现,且随着半径的增大而增大,但并不趋向于1。粒子排列或分布无规律的非晶体,其径向分布函数仅在近程具有波峰,且随着半径的增大趋向于1。
图4为计算得到的不同H2O/Si含量的无定形CS-H 凝胶模型中Ca-O,Ca-H,Ca-Si,Si-Si原子对间的径向分布函数。从图可见不同H2O/Si含量下各原子对间的径向分布函数均在近程出现明显的波峰,随着原子间距的增大,其RDF 值逐渐趋向于1,符合非晶态结构特征即短程有序长程无序。

图4 不同原子对的径向分布函数 (a)Ca-O 原子对;(b)Ca-H 原子对;(c)Ca-Si原子对;(d)Si-Si原子对Fig.4 Radial distribution function of different atom pairs (a)Ca-O pair;(b)Ca-H pair;(c)Ca-Si pair;(d)Si-Si pair
从图4(a)可知,水分子含量的变化对C-S-H 凝胶中Ca-O径向分布函数第一波峰的位置和峰值均有一定的影响,H2O/Si取值分别为1.33和0.8时第一峰值明显下降,H2O/Si取值分别为0.4和0时第一峰值变化不大,这是因为随着水分子含量的增加,Ca离子附近的O原子从硅氧四面体中的O 原子变成了大量水分子中的O原子。从图4(b)可知,随着水分子含量的增高,Ca-H 径向分布函数第一波峰逐渐增大,硅氧四面体形成的硅链骨架层间水分子含量增多,导致Ca原子附近的H 原子逐渐增多。从图4(c)可知,随着水分子含量的增高,C-S-H 凝胶中Ca-Si径向分布函数第一波峰的位置有增大趋势,表明硅链骨架的层间距离增大。从图4(d)可知,随着水分子含量的增高,C-S-H 凝胶中Si-Si径向分布函数第一波峰的位置和峰值均变化不大,这是因为硅链骨架中主要是以Si-O 共价键存在,且两个Si-O共价键的距离是固定的,受水分子的影响较小。
3.2 近邻原子数分析
近邻原子数在一定程度上能够反映模拟对象的局域结构特征,其中最近邻原子数一般被认为是配位数(CN),其表达式为:
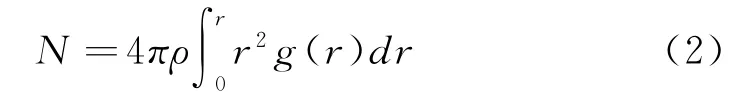
其中,r 为截断半径,ρ 为密度,g(r)为径向分布函数。
图5为通过式(2)计算得到不同H2O/Si含量的无定形C-S-H 凝胶模型中Ca-O,Ca-H,Ca-Si,Si-Si原子对的近邻原子数随截断半径变化的关系曲线。从图可见,随着原子距离的增加,各原子对的近邻原子数均增加且与截断半径r 的关系几乎均呈光滑曲线,但在截断半径r 取值较小时,近邻原子数的取值变化不大。该结果与文献[10]所模拟的稳定无序C-S-H 结构中各原子对的近邻原子数与截断半径r 关系一致。
从图5(a)可见,随着H2O/Si含量的增加,Ca原子附近出现更多的O 原子。但当H2O/Si取值分别为0.4和0时,两条近邻原子数曲线几乎重合,表明Ca原子附近的O 原子数变化不大,随着水分子的减少,硅链骨架间距趋于稳定,且硅链中的O 原子与Ca原子形成稳定的共价键。从图5(b)、(c)可见,近邻原子数曲线平滑,随着硅链骨架间水分子含量的增多,Ca原子附近的H 和Si原子逐渐减少,且结构趋于稳定。从图5(d)可见,近邻原子数曲线在远端均有波动现象,这是由于硅链骨架的出现所致。随着水分子的增多,Si原子附近的Si原子逐渐减少,硅链骨架间距逐渐增大。
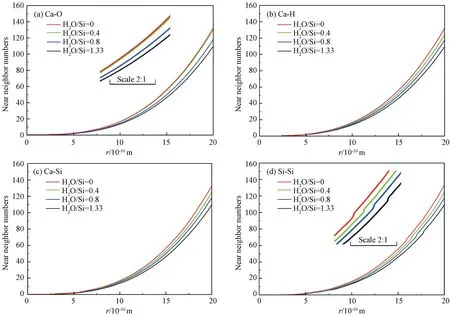
图5 不同原子对的近邻原子数 (a)Ca-O 原子对;(b)Ca-H 原子对;(c)Ca-Si原子对;(d)Si-Si原子对Fig.5 Near neighbor numbers of different atom pairs (a)Ca-O pair;(b)Ca-H pair;(c)Ca-Si pair;(d)Si-Si pair
3.3 力学性能分析
通过Materials studio 软件中Forcite 模块的Mechanical Properties功能对无定形C-S-H 凝胶结构模型进行分子动力学加压模拟,并计算得到模型的力学参量。通过Voigt-Reuss-Hill(VRH)法[22]得到模拟体系的体积模量K 和剪切模量G,并根据式(3)和(4)求解无定形C-S-H 凝胶结构模型的弹性模量和泊松比,其表达式为:

其中,K 为体积模量,G 为剪切模量,E 为杨氏模量,μ为泊松比。
表2为H2O/Si为1.33时无定形C-S-H 凝胶结构体系的力学参量值。可见,本研究模拟C-S-H 凝胶体系的力学模量值与文献[17]的结果吻合较好,略有偏差是由于结构模型的优化参数选取不同所致。与已有文献报道的实验值[23-25]相比,分子动力学模拟结果均有不同程度的偏差,这是由于模拟过程并未考虑实际材料的孔隙及实验过程中的堆积密度等因素所致。
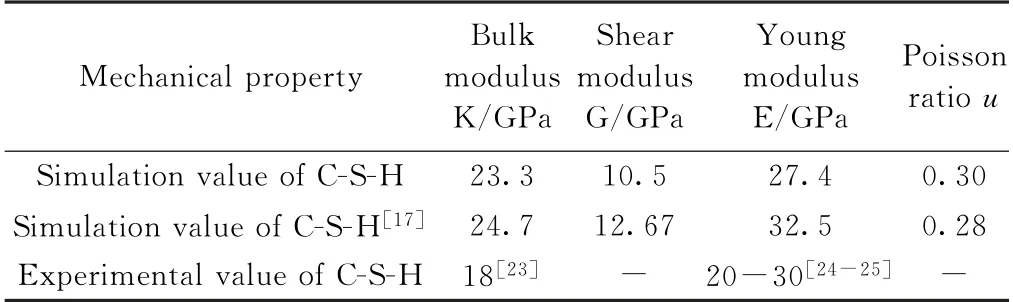
表2 H2 O/Si为1.33时C-S-H 模型的力学参量值Table 2 Mechanical parameters of C-S-H models when H2 O/Si is 1.33
根据式(3)和(4)分别计算出不同水分子含量下无定形C-S-H 凝胶结构体系的杨氏弹性模量E 和泊松比μ。图6为计算得到的不同H2O/Si含量下C-S-H模型的模量值变化曲线。可见,随着H2O/Si比值的增加,材料的杨氏模量E、体积模量K 和剪切模量G均减小,其中剪切模量值变化幅度相对较小。根据不同水分子含量下无定形C-S-H 凝胶结构体系的径向分布函数和近邻原子数分析可知,由于H2O/Si比值越大,凝胶结构体系层间距越大且充斥着大量的水分子,层间粘聚力减小,导致材料更容易发生变形。
4 结 论
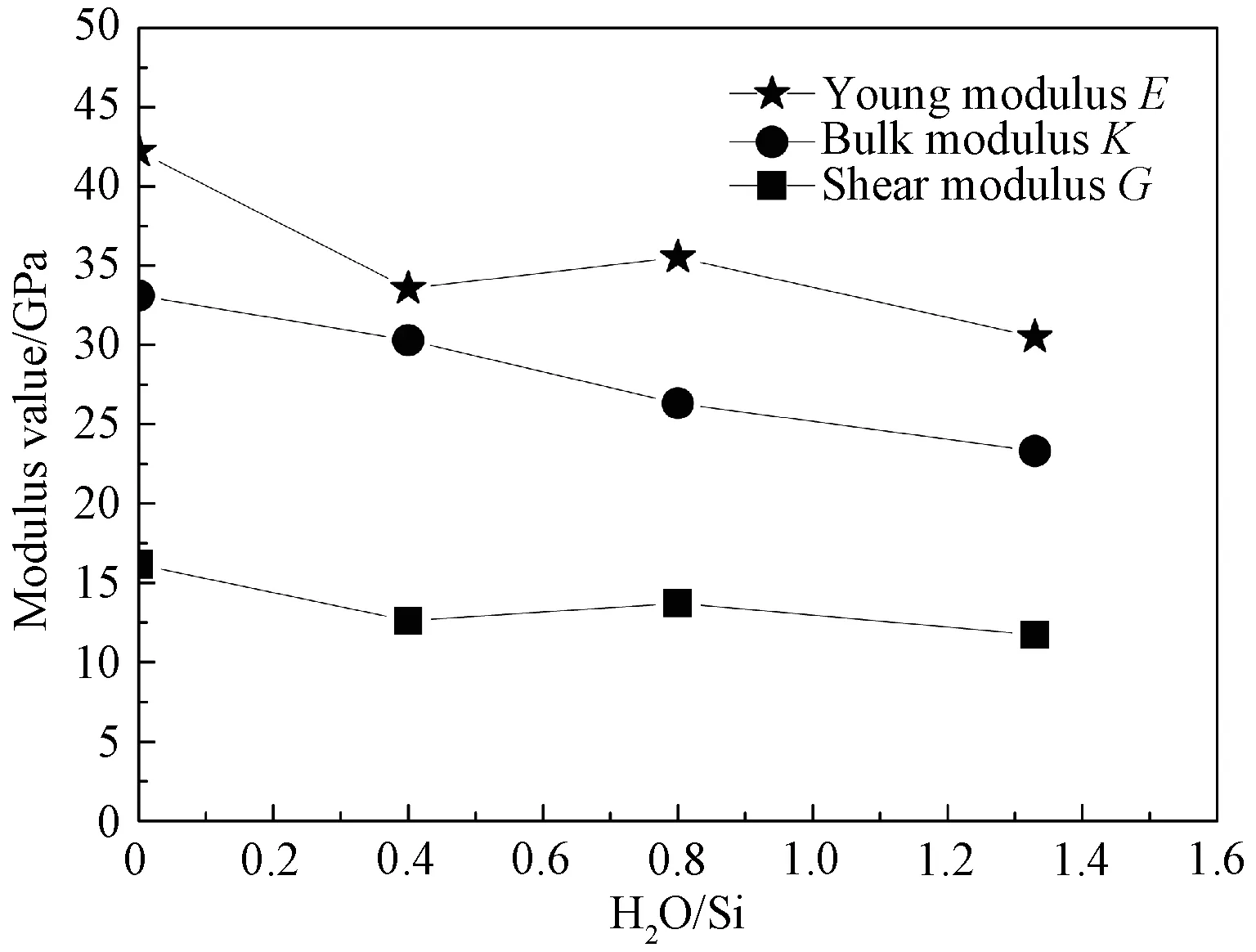
图6 不同H 2 O/Si含量下C-S-H 模型的模量值Fig.6 Modulus values of C-S-H models with different H 2 O/Si content
1.基于随机系统,利用Ca离子、H2O 分子、OH基团和Si3O10集团作为基本单元建立C-S-H 凝胶无定形结构模型,并结合分子动力学方法对模型结构进行优化,得到了不同H2O/Si含量的无定形C-S-H 凝胶体系。基于不同原子对的径向函数分布分析可知,无定型C-S-H 凝胶体系符合非晶态结构特征即短程有序长程无序。
2.通过不同H2O/Si比值下不同原子对的径向分布特征和近邻原子数分析显示随着水分子含量的增高,硅氧四面体形成的硅链骨架层间距增大,层间水分子含量增多。其中当H2O/Si取值小于0.4时,Ca-O原子间的近邻原子数曲线几乎重合,Ca-O 径向分布函数第一峰值变化不大,这是因为当结构内部水分子减少时,Ca离子附近的O 原子从水中的O 原子变成了硅氧四面体中的O 原子,形成新的共价键,结构趋于稳定所致。
3.基于微观结构分析可知,H2O/Si比值越大,结构内层间充斥着越多的水分子,层间粘聚力减弱,材料更易发生变形,导致材料体积模量、杨氏模量和剪切模量均减小,其中剪切模量值变化幅度相对较小。所模拟的C-S-H 凝胶体系的相关模量值与文献结果吻合较好。

