交货时间不确定环境下两级供应链库存决策与契约设计

蔡建湖,张玉洁,徐 芳,黄卫来

(1.浙江工业大学 管理学院，浙江 杭州 310023；2.杭州电子科技大学 管理学院，浙江 杭州 310018；3.华中科技大学 管理学院，湖北 武汉 430074)

0 引言

随着消费者需求层次的不断提升，市场竞争日趋激烈，产品更新换代速度越来越快，产品生命周期也变得越来越短[1]。本文将研究对象定位于短生命周期产品，这类产品往往只有一个相对较短的最佳销售季节，到了季末将贬值。例如，在IT行业，当新一代产品推出后，已上市产品的价值就会下降，并逐代在主流市场中淘汰，因此开发商不得不加快产品研发进程，以应对越来越短的销售周期。在乳制品行业，随着生活水平的提高和饮食结构的改善，人们对短生命周期乳制品(如酸奶、纯奶等)的消费需求呈现出高速增长的态势，而这些短生命周期乳制品大多具有易变质的特点，且需要在生产、加工和运输过程中保证全程冷链，所以如果产品不能及时配送到零售处，将会影响其实际销售周期。在疫苗行业，疫苗的市场需求波动比较频繁，如流感疫苗往往还带有季节性，即过了这个季节后将不能再使用，这给疫苗的供应链管理带来了巨大的挑战。因此，对短生命周期产品而言，供应商能否准时交货是影响客户需求和供应链性能的关键因素[2-5]。一旦交货延迟，产品就无法按时销售，从而缩短实际销售周期，影响供应链成员的利润并造成浪费[6]。

浙江省嘉兴欧尚超市南湖店销售的几乎所有水果都是由嘉兴水果市场供应的。2019年受早春冻害天气的影响，很多水果与去年同期相比出现产量减少、成熟期变晚等情况，因此当嘉兴欧尚超市南湖店发出订单后，嘉兴水果市场无法按时配送的情况时有发生，由于无法及时供货，嘉兴欧尚超市南湖店中该种品类的水果就无法按时上架，顾客需求也就无法满足，从而大大影响了超市的业绩。除了生鲜农产品以外，交货延期的问题在电子产品市场也时有发生。宁波亚虎进出口有限公司在2018年2月初接到了一笔来自荷兰连锁超市Action的订单，订单为在万圣节前夕出售的5万个“魔镜”儿童玩具，Action超市要求订单必须在2018年7月初完成交付。货物从宁波运送至荷兰的海运周期一般为35天，这就意味着该笔订单需要在5月底之前完成生产，宁波亚虎随即与镇海玖美工艺品有限公司签订了生产合同，由镇海玖美代为生产。但由于技术不成熟，镇海玖美生产的“魔镜”儿童玩具中大部分电子元件又都是外购的，这些外购的电子元件在组装时出现了很多质量问题，最终完成生产已经至2018年6月底。为此，宁波亚虎进出口有限公司不得不选择价格十分昂贵的空运来加快交货速度，并为此承担了近30万的损失。因此，交货时间不仅与运输效率有关，还与采购、生产、运输等整个运行流程的效率有关。类似的例子还可以在浙江吉利控股集团、苏州艾吉威机器人有限公司、浙江珂楹实业有限公司等企业的实践中观察到。

目前，已有一些学者开始关注交货时间不确定环境下的供应链管理问题。申成霖等[7]讨论了由一个制造商和两个零售商组成的两阶段分散式供应链系统，并假设制造商的实际交货期大于承诺交货期时会产生一个延迟交货成本，他们主要研究了价格和时间双敏感需求下的供应链定价与交货期联合决策模型，并给出了基于Stackelberg博弈的供应链定价和承诺交货期的最优决策;Safaei等[8]通过定义PERT网络中关键路径的方法来研究交货时间不确定的复杂供应链网络模型，为管理者控制和监控复杂供应链网络模型提供技术支持;Zhao等[9]研究了电子商务环境下两家电子零售商之间的价格竞争和承诺交货提前期竞争，将产品退货考虑在内，并假设其会受到交货时间不确定的影响，检验了竞争中是否存在纳什均衡;Weng等[10]研究了由单个供应商和单个购买商组成的两级供应链,分散供应链中供应商需要在销售季节开始之前交付货物，若货物未能及时交付，则需要通过降低批发价格来补偿购买商的期望利润损失，集成供应链中供应商和购买商共享成本和需求信息，同时决定库存量，研究发现当需求服从均匀分布时，集成供应链中的期望利润总是高于分散供应链中的期望利润;Dai等[11]构建了由一个流感疫苗生产企业和一个零售商组成的两级供应链模型，其中疫苗生产企业采用提前生产和常规生产双生产模式，而零售商面临着不确定的市场需求，提前生产模式保证了疫苗的及时交货，但由于疫苗生产企业不参与疫苗成分的设计(设计由疫苗咨询委员会负责)，生产的疫苗面临着全部报废的风险，常规生产模式生产的疫苗全部可用，但面临着交货时间不确定的风险。为了激励疫苗生产企业提前生产和降低双边际化效应，文献[11]设计了一个回购和延迟补偿联合契约来协调供应链，并实现了供应链总利润在疫苗生产企业和零售商之间的任意分配;Ray等[12]考虑了由一个经销商和一个零售商组成的两级供应链，同时考虑经销商的交货时间不确定和市场需求不确定，主要聚焦于分析集成和分散供应链中供应链成员的最优定价和库存决策。以上研究主要从购买商负责库存管理的视角出发来构建模型，属于零售商管理库存(Retailer Managed Inventory, RMI)，较少涉及供应商管理库存(Vendor Managed Inventory, VMI)。事实上，随着信息技术的发展，VMI模式在实践中得到了越来越多的应用。与RMI模式不同，VMI模式中零售商将库存决策权转移到上游供应商的手中，且与供应商实时分享市场信息[13]。Rad等[14]研究了由一个供应商和两个买家组成的两级供应链模型，其中供应商以有限的生产速率向两个买家提供相同的产品，研究发现，相较于RMI模式，VMI模式可以大幅度地降低供应链的总成本;Yu等[15]基于经济订货批量(Economic Order Quantity, EOQ)模型研究了VMI模式在全球环境下的性能，并假设零售商的需求和供应商的汇率均不确定，研究表明，与RMI模式相比，VMI模式可以通过确定更合适的订单数量来提高供应链的绩效。

契约是改善供应链性能的有效手段。Arvind等[16]研究了由单一供应商和单一零售商组成的简单报童模型，并引入回购、数量柔性、数量折扣、销售回扣和收益分享5种常见的供应链协调契约,研究发现，在RMI模式下的契约均能协调供应链，而VMI模式下数量柔性和销售回扣契约通常不能协调供应链;经有国等[17]从供应链角度出发，考虑了一个由新能源汽车租赁企业和政府组成的新能源汽车租赁二级系统，在需求随机且与推广努力水平相关的市场环境下，探讨了分散决策和集中决策下的最优车队配置和推广努力水平，并通过构建收益共享与成本共担契约来协调供应链，使系统成员获得帕累托改进;Krishnan等[18]研究了由一个供应商和两个零售商组成的两级供应链，其中零售商可以将剩余库存保留至下一阶段进行销售，证明了收益分享契约能够协调与优化该供应链;Palsule-Desai[19]提出的两种收益分享契约均能有效协调供应链，同时在收益潜力平稳下降时，相较于收益独立型的收益分享契约，人们更加倾向于选择收益依赖型的收益分享契约;Li等[20]研究了收益共享契约和成本分担契约对减排努力和企业利润的影响，并讨论了纳什议价模型下的均衡解;Cai等[21]研究了考虑消费者策略型选择行为的VMI供应链，在收益分享契约的基础上结合其他契约协调了供应链，并实现供应链总利润的合理分配;李绩才等[22]将双向期权契约引入产出不确定的两级供应链，研究发现，双向期权契约对供应商生产量和零售商订购量的调控具有良好的柔性，能有效控制不确定因素对供应链产生的影响。

本文针对RMI和VMI两种不同的库存管理模式，分别求得了交货时间确定和交货时间不确定两种情形下供应商与零售商之间的Stackelberg竞争均衡解。同时，在交货时间不确定情形下，通过引入收益分享契约和剩余补贴契约来实现供应链的协调。通过比对现有研究，本文的创新点概括如下：

(1)目前已有文献综合考虑交货时间和需求不确定环境下RMI供应链的库存决策问题，但鲜有文献涉及VMI供应链。本文同时考虑RMI和VMI两种库存管理模式，分析不同库存管理模式下供应链的协调问题。

(2)本文主要研究如何设计不同的契约(共4种契约)来协调供应链，从而减少交货时间不确定对供应链性能的负面影响。本文设计的批发价和收益分享因子联合契约、批发价和剩余补贴联合契约、收益分享因子和剩余补贴联合契约，均可以在协调供应链的同时实现供应链总利润的任意分配。

(3)目前鲜有文献关注交货时间不确定程度对供应链契约有效性的影响，本文对此进行了扩展研究。研究表明，如果以供应商交货时间确定时的离散供应链为比较基准，则当交货时间不确定程度满足一定范围时，本文设计的联合契约也能实现供应链性能的帕累托改进。

(4)本文在不同的库存管理模式下均提供了多样化的契约设计方案，使本文的研究成果能适应供应链在实际运行过程中的不同情形。这样的研究思路，增强了本文研究成果在实践中的应用价值。

1 模型的建立

考虑由一个供应商和一个零售商组成的两级供应链，零售商销售一种具有明确销售起点和销售终点的产品，销售季节的总时间长度为b，即共有b个销售时间单位，假设每个销售时间单位销售一个单位产品，则b个销售时间单位一共销售b个单位的产品。用y表示订单完成时间，即供应商在y时间点完成订单配送，y=0表示刚好在销售季节开始的时间点完成交货。因此，当y≤0时，表示供应商能够准时交货；当y>0时，表示供应商不能准时交货，并延长了y个时间单位，如图1所示。

Ej(qj)=pEmin(qj,D)-tqj+sE(qj-D)+

(1)

(2)

2 RMI模式下的库存决策模型

首先，考虑一个常见的收益分享契约来协调供应链，即在单位批发价格wa的基础上引入一个收益分享因子k(0≤k≤1)。为方便，将以上契约记为{wa,k}契约。根据{wa,k}契约，零售商在订购产品时首先向供应商支付批发价wa，当产品销售出去后再与供应商进行收益分享。每销售一个零售价格为p的产品，供应商获益kp，而零售商获益(1-k)p。同样地，对季末剩余产品，每处理一单位产品，供应商获益ks，零售商获益(1-k)s。在RMI模式下，供应链的决策流程可以描述如下：

(1)由供应商决定批发价wa和收益分享因子k。

(2)零售商根据供应商给出的批发价格和收益分享因子决定订购量qR1。

根据逆向归纳法，在给定供应商设定的契约参数条件下，零售商的期望利润为：

f(x|y,y>0)g(y)dxdy]。

(3)

(4)

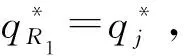
wa=(1-k)t。

(5)

当式(5)成立时，供应商的期望利润为：

(6)

零售商的期望利润为：

(7)

命题1在{wa,k}契约中，满足wa=(1-k)t时，供应链总是处于协调状态。同时，供应商可以通过调节收益分享因子和批发价格来实现供应链总利润在成员之间的任意划分。

根据命题1，在{wa,k}契约中，必定存在一个帕累托区间，供应商可以在该区间内选择合适的收益分享因子和批发价格，使得供应链成员的期望利润与未引入契约之前相比都得到提升，从而降低交货时间不确定对供应商与零售商造成的影响。

在对浙江珂楹实业有限公司进行调研时，笔者发现，在一些“战略开发”项目中，面料供应商会首先向珂楹收取一个较低的批发价格，等服装卖出后，再按照一定的比例向珂楹收取销售收益分成。这样的交易方式可以激励珂楹多订购，并在一定程度上帮助珂楹和面料供应商降低延期交货带来的影响，这与命题1的结论相符。

除了收益分享契约以外，剩余补贴契约也同样可以协调供应链。即零售商在订购产品时首先向供应商支付一个单位批发价格wa，销售季节结束后未销售完的产品供应商再给零售商一个单位补贴费用v，将以上契约记为{wa,v}契约。根据{wa,v}契约，在RMI模式下，供应链的决策流程可以描述如下：

(1)由供应商决定批发价格wa和补贴费用v。

(2)零售商根据供应商给出的批发价格和补贴费用决定订购量qR2。

根据逆向归纳法，此时零售商的期望利润为：

qR2f(x|y,y>0)g(y)dxdy]-

(qR2-x)f(x|y,y>0)g(y)dxdy]。

(8)

(9)

(10)

当式(10)成立时，供应商的期望利润为：

(11)

零售商的期望利润为：

(12)

根据命题2，{wa,v}契约具有和{wa,k}契约类似的性能，即相对于交货时间不确定的离散供应链，使用{wa,v}契约必定存在一个帕累托区间，使得零售商和供应商的期望利润都得到提高。

在文献[10]的研究中，为确保零售商的期望利润不受交货时间不确定的影响，供应商不得不降低批发价，但是作者没有考虑如何通过优化供应链整体性能来提升供应链成员的收益。而通过{wa,k}契约或者{wa,v}契约，供应商在一定条件下可以确保零售商的期望利润不受损，同时得到集成供应链的剩余利润，这实际上在增强供应商竞争力的同时，也提升了供应链的性能。如果将{wa,k}契约和{wa,v}契约下的供应链性能与供应商交货时间确定的RMI离散供应链的性能进行比较，得到以下命题。

命题3在{wa,k}契约和{wa,v}契约中，与供应商具有准时交货能力的RMI离散供应链相比，①当交货时间不确定程度满足α∈[0,0.675 8]时，供应商不但可以通过合理设计契约来确保零售商的期望利润不受损，而且能保证自身的期望利润不受损，甚至有所增加；②当交货时间不确定程度满足α∈(0.675 8,0.999 1]时，供应商可以通过合理设计契约来确保零售商的期望利润不受损，但此时供应商自身的期望利润将降低；③当交货时间不确定程度满足α∈(0.999 1,1]时，供应商无法通过设计契约来确保零售商的期望利润不受损。

证明在{wa,k}契约中：

由命题3的(1)可知，当交货时间不确定程度α较低(即满足α∈[0,0.675 8])时，供应商不但可以确保零售商的期望利润不受损，而且消除了交货时间不确定对自身期望利润造成的负面影响；由命题3的(2)可知，当交货时间不确定程度α相对较高(即α∈(0.675 8,0.999 1])时，供应商可以通过合理设计契约使零售商的期望利润不受损，同时自己获得集成供应链的剩余期望利润；根据命题3的(3)可知，当交货时间不确定程度α极高(即α∈(0.999 1,1])时，契约失效。此时，当市场上有其他供应商出现时，零售商可能会转而选择供货能力更强的供应商。显然，交货不确定程度极高的供应商在市场中将缺乏竞争力。命题3表明，相对于交货时间确定的RMI离散供应链，供应商可以通过设计合理的契约来有效提升交货时间不确定的RMI供应链性能，特别地，当供应商的交货时间不确定程度较低时，契约能完全消除供应商交货时间不确定带来的负面影响。

命题3中，{wa,k}契约和{wa,v}契约很好地扮演了风险共担的角色，使得供应链成员在作决策时能从供应链整体的角度出发，增强交货时间不确定供应链的竞争力。供应链成员通过契约建立交易模式后，即使市面上出现能力更强(例如，交货时间更稳定)的供应商，成员之间的这种合作关系也很难被打破。例如很多大型超市在与供应商合作时，首先会确定交易模式，这些交易模式可通过收益分享契约、批发价契约、剩余补贴契约等形式建立。一旦合同签订，即使市场上出现其他供货更稳定的供应商，这些大型超市也不会贸然更换供应商。

虽然{wa,k}契约和{wa,v}契约均能协调供应链，但两种契约也存在一些不同点：

3 VMI模式下的库存决策模型

st(4p+t-2s)-2p(s2+t2)=0。

(13)

接下来，同样考虑一个常见的收益分享契约来优化供应链性能。在VMI模式下，批发价格wb和收益分享因子φ(0≤φ≤1)的决定权掌握在零售商的手中，而由供应商来选择最优的库存量。和RMI模式类似，假设每销售单位产品，供应商获益φp，零售商获益为(1-φ)p。同时，每处理单位产品，零售商获益(1-φ)s，供应商获益φs。为方便，将以上契约记为{wb,φ}契约。在{wb,φ}契约下，供应链的决策流程描述如下：

(1)由零售商决定批发价格wb和收益分享因子φ；

(2)供应商根据零售商给出的批发价和收益分享因子决定库存量qV1。

根据逆向归纳法，此时供应商的期望利润为：

g(y)dxdy]。

(14)

(15)

wb=(1-φ)t。

(16)

当式(16)成立时，零售商的期望利润为：

(17)

供应商的期望利润为：

(18)

命题5在{wb,φ}契约中，满足wb=(1-φ)t时，供应链总是协调的。同时，零售商可以通过调节收益分享因子和批发价格来实现供应链总利润的任意划分。

尽管通过调节批发价和收益分享因子能够协调供应链，但是在零售商主导的VMI模式中，很多零售商都会认为这样的交易方式太过复杂，因为其必须先向供应商支付部分批发价格，在销售完毕之后再向供应商支付部分收益份额。因此，不设置批发价这种管理模式在零售商主导的VMI模式中非常普遍，即供应商在向零售商供货时，将不能得到批发价，而是等到销售季节结束，供应商直接按照一定的比例从零售商处得到相应的利润分成。此时，零售商首先确定收益分享因子φ，供应商确定库存量qV2。

根据逆向归纳法，供应商的期望利润为：

(qV2-x)f(x|y,y>0)g(y)dxdy]。

(19)

(20)

预料到供应商的反应函数，零售商的期望利润为：

(21)

为增加供应商的生产投入，这里考虑引入剩余补贴契约来协调供应链，即对季末未售出的产品，零售商提供给供应商一个单位补贴费用v，这里将以上契约称为{v,φ}契约。此时，供应链的决策流程可以描述如下：

(1)零售商确定收益分享因子φ和补贴费用v；

(2)供应商根据零售商给出的收益分享因子和补贴费用决定库存量qV3。

在给定零售商设定的契约参数条件下，供应商的期望利润为：

f(x|y,y>0)g(y)dxdy]-tqV3+(φs+v)

(22)

(23)

(24)

当式(24)成立时，零售商的期望利润为：

(25)

供应商的期望利润为：

(26)

根据命题5和命题6，{v,φ}契约具有与{wb,φ}契约类似的性能，即能够改进VMI供应链的性能，又能在一定范围内降低交货时间不确定对供应商与零售商造成的影响。此时，若零售商所处的市场中供应商的供应能力均不稳定，则作为博弈主导者的零售商只能通过契约来改进供应链本身的性能；若零售商所处的市场中有供应稳定的供应商，则零售商也同样有一个机会成本去选择交货能力更强的供应商。如果将{v,φ}契约和{wb,φ}契约下的供应链性能与供应商交货时间确定的VMI离散供应链的性能进行比较，我们得到以下命题。

命题7在{wb,φ}契约和{v,φ}契约中，与具有准时交货能力的VMI离散供应链相比：

证明在{wb,φ}契约中：

命题7表明，相对于供应商能准时交货的VMI离散供应链，零售商可以通过合理设计契约来改善供应商交货时间不确定的VMI供应链的性能。特别地，当供应商的交货时间不确定程度较低时，契约能完全消除供应商交货时间不确定带来的负面影响。因此，在VMI模式中，和命题3类似，{wb,φ}契约和{v,φ}契约也为构建供应链成员之间的紧密合作关系创造了有利条件，实现了供应链协调以及协调利润在成员之间的任意分配。

命题8在{v,φ}和{wb,φ}契约下，若零售商选择相同的收益分享因子φ，则为协调供应链，有v>wb。

证明：对比(16)式和(24)式易得到此命题。证毕。

由命题8可知，在{v,φ}和{wb,φ}契约下，当供应链处于协调状态时，若零售商选择相同的收益分享因子φ，我们有v>wb，此时在{v,φ}契约中零售商向供应商支付的补贴费用要高于在{wb,φ}契约中零售商向供应商支付的批发价格，这样的性质表明，尽管两种契约都可以协调供应链，但是在实际应用中有着不同的特性，当供应链成员之间采用{v,φ}契约时，供应商在向零售商供货时，将无法得到批发价格，只能当产品卖出去之后才能得到一定比例分成，因此其有可能为了防范供应链风险而选择比较低的库存水平，而零售商为了鼓励供应商提升库存水平，会选择相对较高的补贴费用，来提升供应链性能。

本文所有的解析结论如表1所示。

表1 本文相关的解析结论

4 数值分析

(1)分析交货时间不确定程度α给定时，契约对供应链成员期望利润的影响。

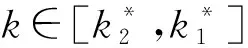
同理，由命题2、命题5和命题6得到的其他几个协调契约中，供应商与零售商的期望利润变动情况与图2类似，与RMI模式不同的是，在VMI模式中，零售商掌握竞争的主导权。

特别地，在{v,φ}和{wb,φ}两种不同的契约下，若此时零售商选择相同的收益分享因子φ=0.6，其他参数条件设置和ω1相同，则为协调供应链，我们有wb=4，v=4.5，这里v>wb，符合命题8的结论。

(2)分析交货时间不确定程度α未给定时，契约对供应链成员期望利润的影响。

假设供应链所处的市场环境中，存在其他有稳定交货能力的供应商，此时供应链成员之间使用契约能在一定条件下改善供应链的性能，增加交货时间不确定供应链的竞争力。

由表2可以看出，交货时间不确定程度α的增加会导致集成和离散供应链的库存水平、供应链成员的期望利润下降，这说明随着交货不确定程度的增加，决策者会适当减少库存水平以防范不确定带来的风险。同时，随着交货时间不确定程度α的不断增加，ΔE也不断下降，这说明契约对改进供应商交货时间不确定的RMI供应链性能的有效性随着α的增加而不断减弱。

表2 交货时间不确定程度α的变化对供应链成员的库存水平以及ΔE的影响

为更加直观地表示出交货时间不确定程度α对契约有效性的影响，结合命题3，分析α在不同的区间时，使用契约是否能有效改善供应链的性能。ΔE随α的变动情况如图3所示。

由图3可知，对比交货时间确定的RMI离散供应链，①当α在α∈[0,0.675 8]内变动时，ΔE≥0，即契约能完全消除交货不确定带来的风险，此时供应商可以通过合理设计契约来确保零售商的期望利润不受交货时间不确定的损害，同时也能保证自身的期望利润不受损。特别地，当α<0.675 8时，供应商在确保零售商的期望利润不受损的同时，自身的利润还能有所增加；②当α在α∈(0.675 8,0.999 1]内变动时，-888.89≤ΔE<0，即契约只能消除交货不确定带来的部分风险，此时供应商可以通过合理设计契约来确保零售商的期望利润不受损，但自身的利润会有所下降；③当α在α∈(0.999 1,0]内变动时，ΔE<-888.89，此时契约失效，零售商可能会转而选择其他供货能力更强的供应商。

表3 交货时间不确定程度α的变化对供应链成员的库存水平以及ΔH的影响

由表3可知，交货时间不确定程度α的增加会导致集成和离散供应链的库存水平、供应链成员的期望利润下降，这说明随着交货不确定程度的增加，决策者会适当减少库存水平以防范不确定带来的风险。同时，随着交货时间不确定程度α的不断增加，ΔH也不断下降，这说明契约对改进供应链性能的有效性随着α的增加而不断减弱。

为更加直观地表示出交货时间不确定程度α对契约有效性的影响，结合命题7，分析α在不同的区间时，使用契约是否能有效改善供应链的性能。ΔH随α的变动情况如图4所示。

由图4可知，对比交货时间确定的VMI离散供应链，①当α∈[0,0.528 7]内变动时，ΔH≥0，即契约能完全消除交货不确定带来的风险，此时零售商可以通过合理设计契约来确保自身的期望利润不受损，同时也能保证供应商的期望利润不受损，特别地，当α<0.528 7时，零售商在确保供应商的期望利润不受损的同时，自身的利润还能有所增加；②当α∈(0.528 7,0.826 9]内变动时，-184.67≤ΔH<0，即契约只能消除交货不确定带来的部分风险，此时零售商可以通过合理设计契约来确保自身的期望利润不受损，但无法保证供应商的利润不受交货时间不确定的损害；③当α∈(0.826 9,1]内变动时，ΔH<-184.67，此时契约失效，零售商可能会转而选择其他供货能力更强的供应商。

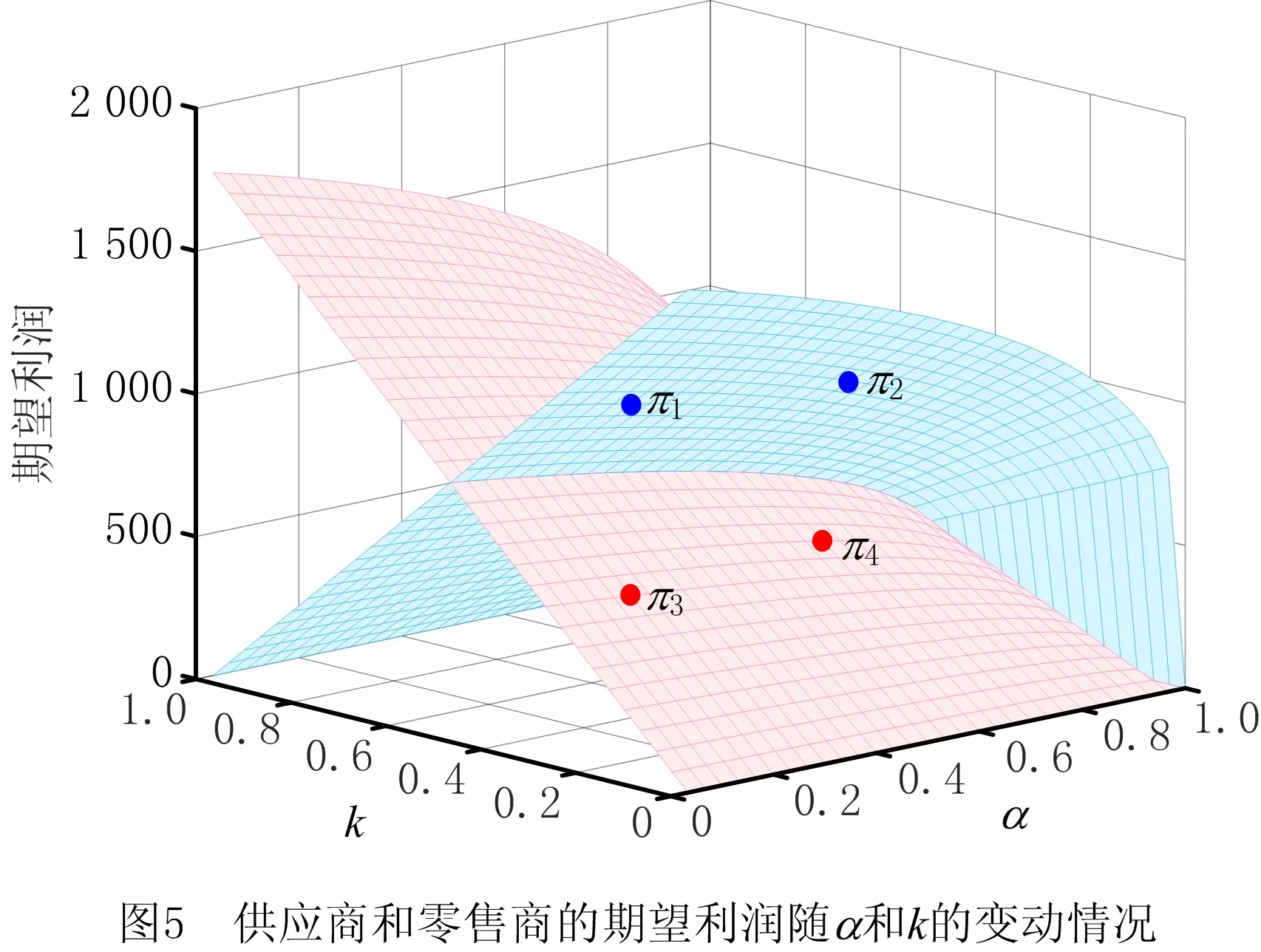
最后，为了更加直观地说明当交货时间不确定程度α改变时，博弈主导者如何通过契约来改进供应链性能，以RMI模式为例，分析当α和k同时变动时，供应商和零售商期望利润的改变情况。这里，再次取参数组ω2={p=50,t=10,s=5,b=100}，分析当α在α∈[0,1]，k在k∈[0,1]内变动时，供应链成员期望利润的变化趋势。如图5所示，π3点和π4点所在的区域面积表示供应商的期望利润，π1点和π2点所在的区域面积表示零售商的期望利润，且π1=(0.200 0,0.300 0,1 176.00)，π2=(0.525 0,0.200 0,1 176.00)，π3=(0.200 0,0.300 0,504.20)，π4=(0.633 3,0.366 4,504.20)。因此，π1和π2分别表示取不同的(α,k)组合时，零售商能够获得的期望利润；π3和π4表示取不同的(α,k)组合时，供应商能够获得的期望利润。对比π1和π2发现，当交货时间不确定程度α从π1的0.200 0增加至π2的0.525 0时，作为博弈主导者的供应商如果将收益分享因子从π1的0.3调至π2的0.2时，就能使零售商的期望利润保持不变，即始终为1 176.00；同理，对比π3和π4发现，当交货时间不确定程度α从π3的0.200 0增加至π4的0.633 3时，作为博弈主导者的供应商如果将收益分享因子从π3的0.300 0调至π4的0.366 4时，就能使自身的期望利润保持不变，即始终为504.20，这也进一步说明了契约对降低交货时间不确定所带来的风险的有效性。

5 结束语

本文研究了交货时间不确定环境下两级供应链的竞争模型和契约设计。研究发现，在零售商管理库存和供应商管理库存两种不同的库存模式下，批发价和收益分享因子联合契约、批发价和剩余补贴联合契约、收益分享因子和剩余补贴联合契约，均可以在协调供应链的同时实现供应链总利润的任意分配，从而减少交货时间不确定对供应链性能的负面影响。契约的影响包含两个方面：①相对于交货不确定环境下的离散供应链，契约一定能够实现供应链性能的帕累托改进，使得供应链成员都能获得更多的期望利润；②相对于能准时交货的离散供应链，契约也能在一定的条件下改善供应链的性能，增强交货时间不确定供应链的竞争力。当供应商的交货时间不确定时，也有零售商会通过选择多个供应商来降低缺货风险。因此，在一个两级供应链系统中，研究多个供应商如何协同供货是今后可以扩展的一个方向。