多障碍环境下机械臂避障路径规划
陈满意,张 桥,,张 弓,梁济民,侯至丞,杨文林,徐 征,王 建
(1.武汉理工大学 机电工程学院,湖北 武汉 430070;2.广州中国科学院先进技术研究所,广东 广州 511458;3.中国科学院深圳先进技术研究院,广东 深圳 518055)
1 问题的描述
如今,协作机器人发展迅速,在手机等3C行业发挥的作用越来越大,如图1所示为多机器人协作进行手机配件装盒。由于机器人布置密集,工作的时候存在很多干涉碰撞问题,因此协作机器人避障路径规划成为了一大关键突破点,众多学者都对其进行了研究。避障路径规划是指在工作空间存在障碍物的情况下,机器人在有限的时间内规划出一条无碰撞的路径[1-2],由于工业机械臂的应用环境越来越复杂,避障路径规划的作用也越来越重要。

人工势场法由Khatib[3]于1985年提出,其规划的路径质量高,但是容易陷入局部极小而发生振荡。快速扩展随机树(Rapidly-exploring Random Tree, RRT)算法由Lavalle[4]于1998年正式提出,其在多障碍物环境下搜索成功率很高,但是搜索随机性大、效率低。很多学者对这两种算法分别进行了改进,姬伟等[5]提出一种基于虚拟目标点的人工势场法用于机械臂逃离局部极小值;Wang等[6]提出一种基于改进吸引力势函数的人工势场法,实现机械臂关节角速度的平滑过渡;Seyyed等[7]提出一种基于代价函数的人工势场法,用于解决路径搜索容易陷入局部极小值和目标不可达的问题;陈晋音等[8]提出改进的EB_RRT算法,解决障碍物附近路径搜索迭代次数过高的问题;Wei等[9]提出一种S-RRT路径规划算法,提高路径节点扩展效率;何兆楚等[10]提出人工势场-RRT算法,解决路径搜索容易陷入局部极小值的问题。
以上研究都是在机械臂的关节空间进行规划,需要将障碍物转换到关节空间,计算复杂。为此,本文在笛卡尔坐标空间进行机械臂避障路径规划,为了在每个步长都取得最优的逆运动学关节角,保证前后步长对应关节角度值变化连续性,参考Craig[11]对机械臂运动学逆解的处理,提出最短行程逆解算法;参考Ketchel等[12]提出的包围球和圆柱包络法对障碍物和机械臂连杆进行近似模拟,检测机械臂连杆和障碍物的碰撞,提出一种低振荡人工势场—自适应快速扩展随机树(Adaptive RRT, ARRT)混合算法,先采用低振荡人工势场法进行搜索,当遇到局部极小、碰撞等情况时,切换成ARRT算法进行搜索,两种算法结合使用,直至到达目标点。低振荡人工势场法降低了路径的振荡程度,ARRT算法则在经典RRT算法的基础上加入自适应避障策略,提高搜索效率。另外,为提高路径质量,提出冗余路径节点删除策略,并使用四次贝塞尔曲线[13]对路径进行拟合。
2 算法原理
2.1 碰撞检测方法
本文研究对象为六自由度机械臂,碰撞检测指的是障碍物与机械臂连杆的碰撞检测,而实际工程应用中障碍物的外形一般不规则,很难通过精确的数学公式进行表达。因此,本文采用包围球对障碍物进行近似模拟,采用圆柱包络法对机械臂连杆进行简化,如图2所示。该方法虽然增加了障碍物和机器人本体的区域,但是大大简化了计算量。

在三维空间内计算障碍物中心点和每根连杆所在直线的距离dis,比较dis和R+r的大小,若dis≥R+r,则障碍物和连杆没有发生碰撞;若障碍物与机器人各连杆均满足无碰撞条件,则机器人当前状态满足无碰撞条件。
2.2 最短行程解算法
本次路径规划研究在笛卡尔空间完成,根据机械臂末端位姿采用逆运动学求解最多可求得八组解,为了在每个步长都取得最优的逆运动学关节角,保证前后步长对应关节角度值变化连续性,提出了最短行程逆解算法,因此两个步长之间每个关节的角度变化需尽可能小,即实现“最短行程”。机械臂空间搜索每移动一个步长的最短行程解即使得每一个关节角度变化最小,求出关节角变量的L1范数最小值即可,又因为机械臂6个连杆中靠近末端的连杆主要决定机械臂末端执行器的姿态,远离末端的连杆主要决定机械臂末端执行器的位置,所以求最短行程解时需要加权,满足式(1)的各关节角度值即为最短行程解:
(1)
式中:Δθi为每个关节角度值的变化量;ωi为每个关节角度值变化量的加权系数。
2.3 低振荡人工势场法
人工势场法是局部路径规划方法,目标点对机械臂产生引力作用,障碍物对机械臂产生排斥力作用,引力和斥力的合力方向决定机器人运动方向,如图3所示。
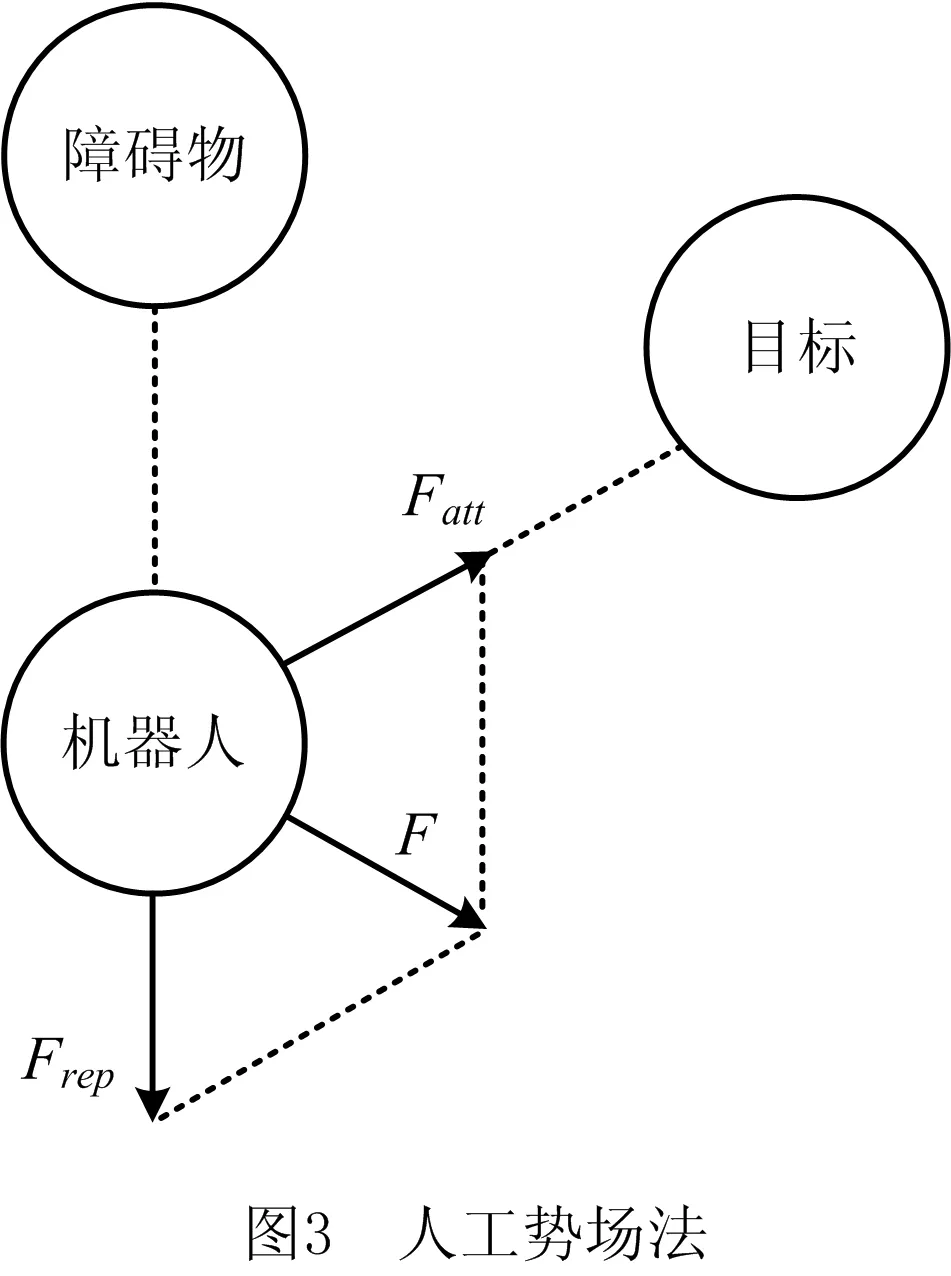

(2)
(3)
其中:Uatt为引力势函数;ka为引力系数,Probot为机器人当前位置;Pg为目标点位置;Urep表示斥力势函数;kr为斥力系数;l为机器人与障碍物之间的距离;l0为斥力场作用范围。对于如何选择其中的常量值,文献[14]进行了详细的论述。
机器人的势能总和
U=Uatt+Urep。
(4)
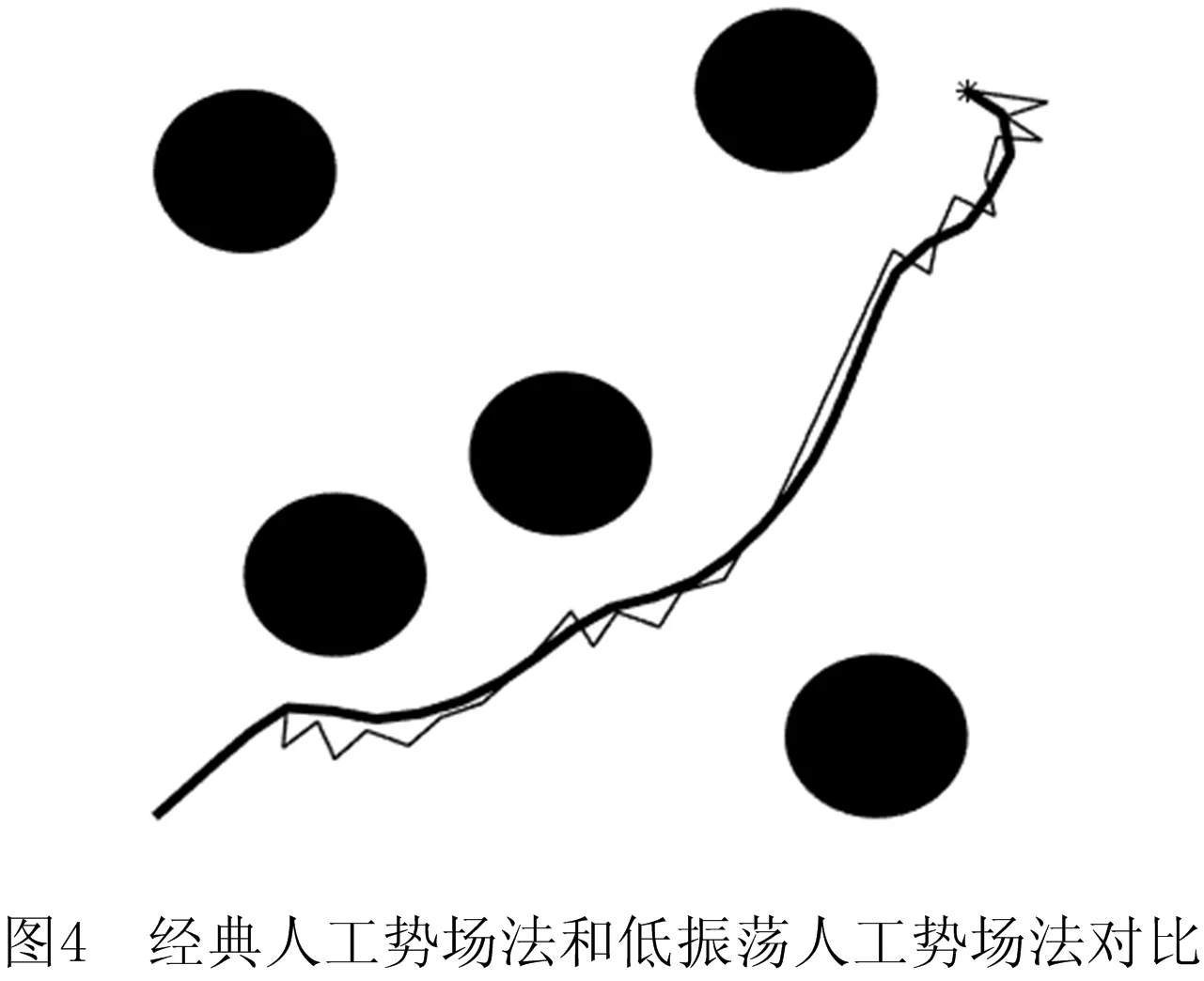
如图4所示为经典人工势场法和低振荡人工势场法的仿真效果对比。在障碍物、步长等其他条件均相同的情况下,图中粗线代表低振荡人工势场法规划的路径,其振荡幅度相比于经典人工势场法路径明显降低。
2.4 ARRT算法
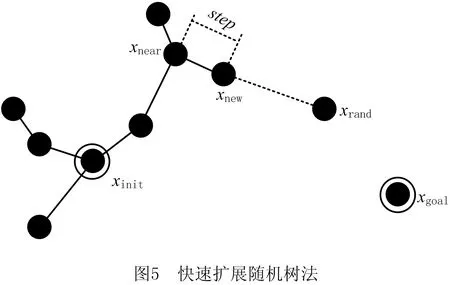
经典RRT算法的原理如图5所示,机器人每一次路径搜索都需要寻找一个随机点xrand,在已经存在的路径节点中选取距离xrand最近的点xnear并以步长step朝着随机点xrand的方向进行扩展,以此方式搜索路径直至到达终点。
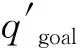
(x1-x0)(x-x0)+(y1-y0)(y-y0)+
(z1-z0)(z-z0)=0。
(5)
则通过式(5)可以计算
zE=(x1-x0)(x0+cosθ-x0)+
(y1-y0)(y+sinθ-y0)/z1-z0+z0。
(6)

x2=x0+
y2=y0+
z2=z0+
(7)
如表1所示为经典RRT算法和ARRT算法经过MATLAB仿真分析之后的迭代次数对比,在障碍物、步长等其他条件均相同的情况下仿真分析20次,ARRT算法的平均迭代次数相比于经典的RRT算法的平均迭代次数从143.8次降低到了89.8次,有效地提高了障碍物附近机器人避障路径搜索的效率。

表1 经典RRT和ARRT平均迭代次数对比
3 低振荡人工势场-ARRT混合算法
3.1 人工势场法和RRT算法的结合
利用一种算法的优点来弥补另外一种算法的缺点是学术研究的重要思路[15-16],本文提出低振荡人工势场—ARRT混合算法,机器人先采用低振荡人工势场法进行搜索,当遇到局部极小、碰撞等情况时,切换成ARRT算法进行搜索,两种方法结合使用,直至到达目标点。判断碰撞的方法已经在前文叙述,判断机器人由于局部极小值点等引起的振荡则采用以下策略。
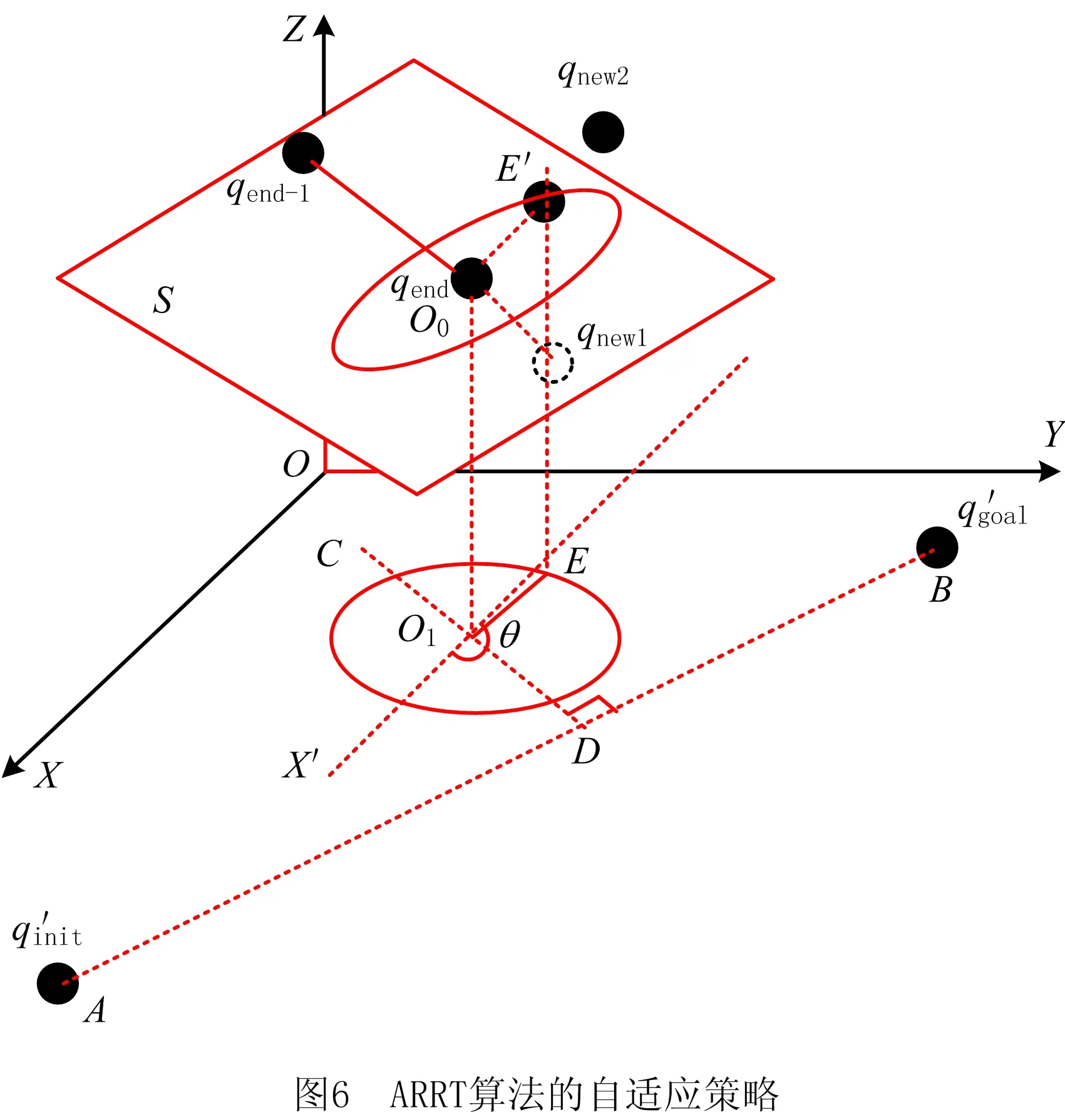
当前节点为qend,其前一个节点为qend-1,qnew为当前确定的新的路径节点。由图7中夹角θ可以看出,qend-1、qend、qnew这3个节点已经有出现振荡的趋势,因此判断夹角θ的大小即可判断人工势场法是否出现振荡,在平面内和三维空间都适用。设qend坐标为A(x0,y0,z0),qend-1坐标为B(x1,y1,z1),qnew坐标为C(x2,y2,z2),则由余弦定理:
(8)
具体阈值取θ≤π/6时,判定人工势场法可能出现振荡,切换为ARRT算法进行搜索,逃离之后再切换回低振荡人工势场法进行搜索。
算法伪代码如下:
low-oscillation artificial potential field-ARRT hybrid
1.T←init(qinit);
2.qnew←Low-Oscillation_Artificial_Potential(x);
3.Collosion_detection(qnew) or Oscillation_detection(qnew,qend,qend-1) then
4.qnew←∅
5.qnew←ARRT(x);
6.If Collosion_detection(qnew)
7.Return advanced;
8.Else
9.If qnew=qendthen
10.Return Reached;
11.Else
12.Extend(T,qnew)
13.Return Low-Oscillation_Artificial_Potential(x);
14.Else
15.If qnew=qendthen
16.Return Reached;
17.Else
18.Extend(T,qnew);
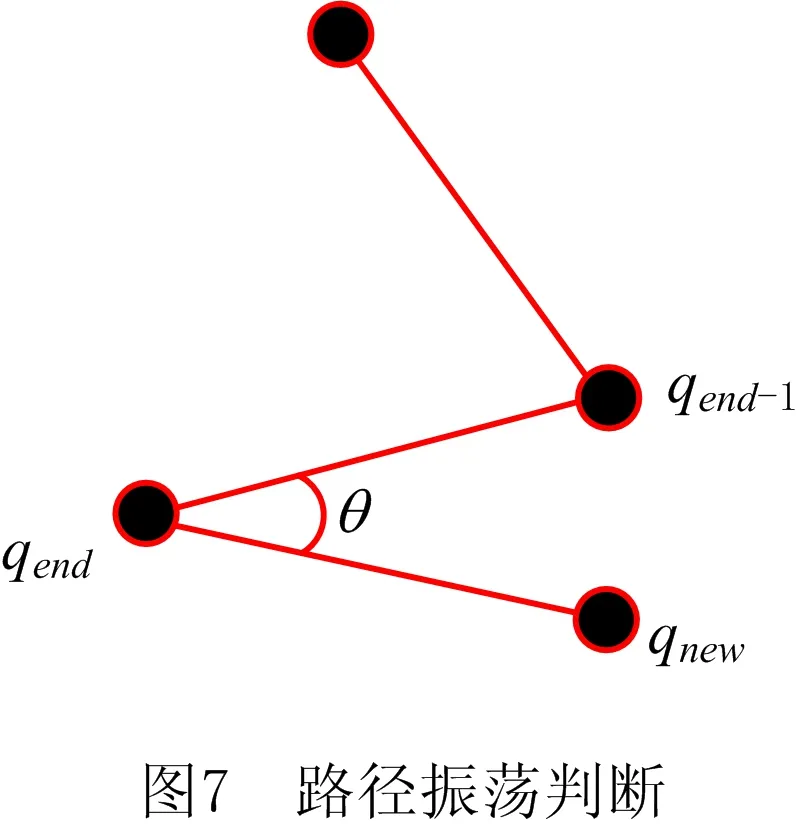
算法流程图如图8所示。使用最短行程解算法来保证机械臂在笛卡尔空间规划的关节角度变化连续性,规划过程在笛卡尔空间进行,不需要将障碍物转化到关节空间,可节省很大的计算量。
2.2 路径优化
2.2.1 冗余路径节点删除策略
由于RRT算法的随机性,Sudhakara等[17]提出RRT*算法进行节点路径的优化。但是RRT*的算法所使用的路径优化策略只针对于单独使用RRT算法的情况,因此本文提出一种冗余路径节点删除策略,其步骤描述如下:
(1)低振荡人工势场法切换到ARRT算法。
(2)定义Tree数组,Tree相当于一个节点容器用来收集低振荡人工势场—ARRT混合算法的节点。定义RRTtree数组,该数组用来收集ARRT算法的节点,确定本次ARRT扩展的新节点qnew。
(3)新增节点qnew到Tree数组,qnew的前一个节点,也就是当前节点为qend,将qend和qnew到RRTtree数组。
(4)按照节点添加的时间先后顺序,在RRTtree数组中从第一个节点开始计算和qnew的距离distance,已知步长d,假设满足如下条件:
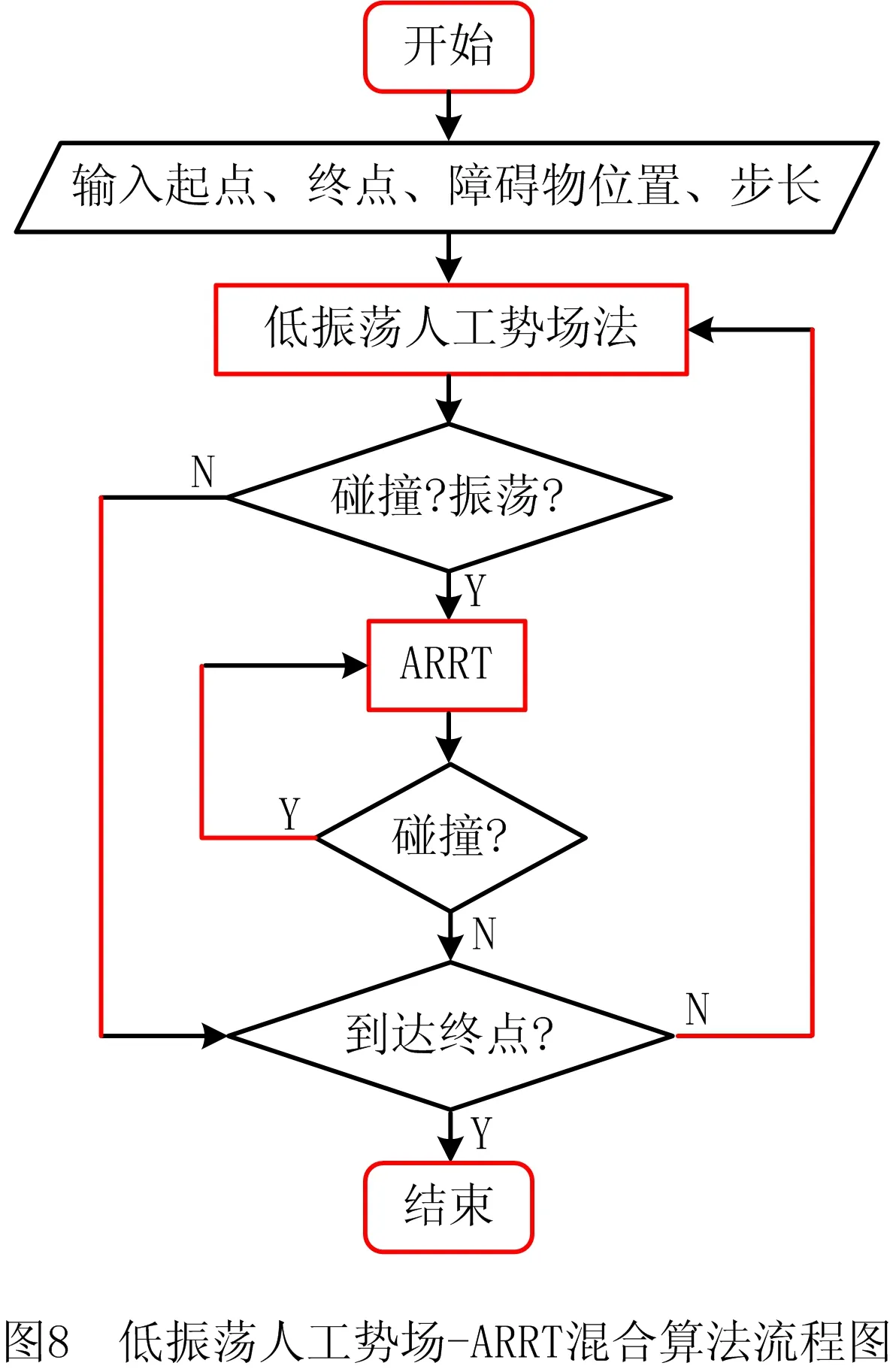
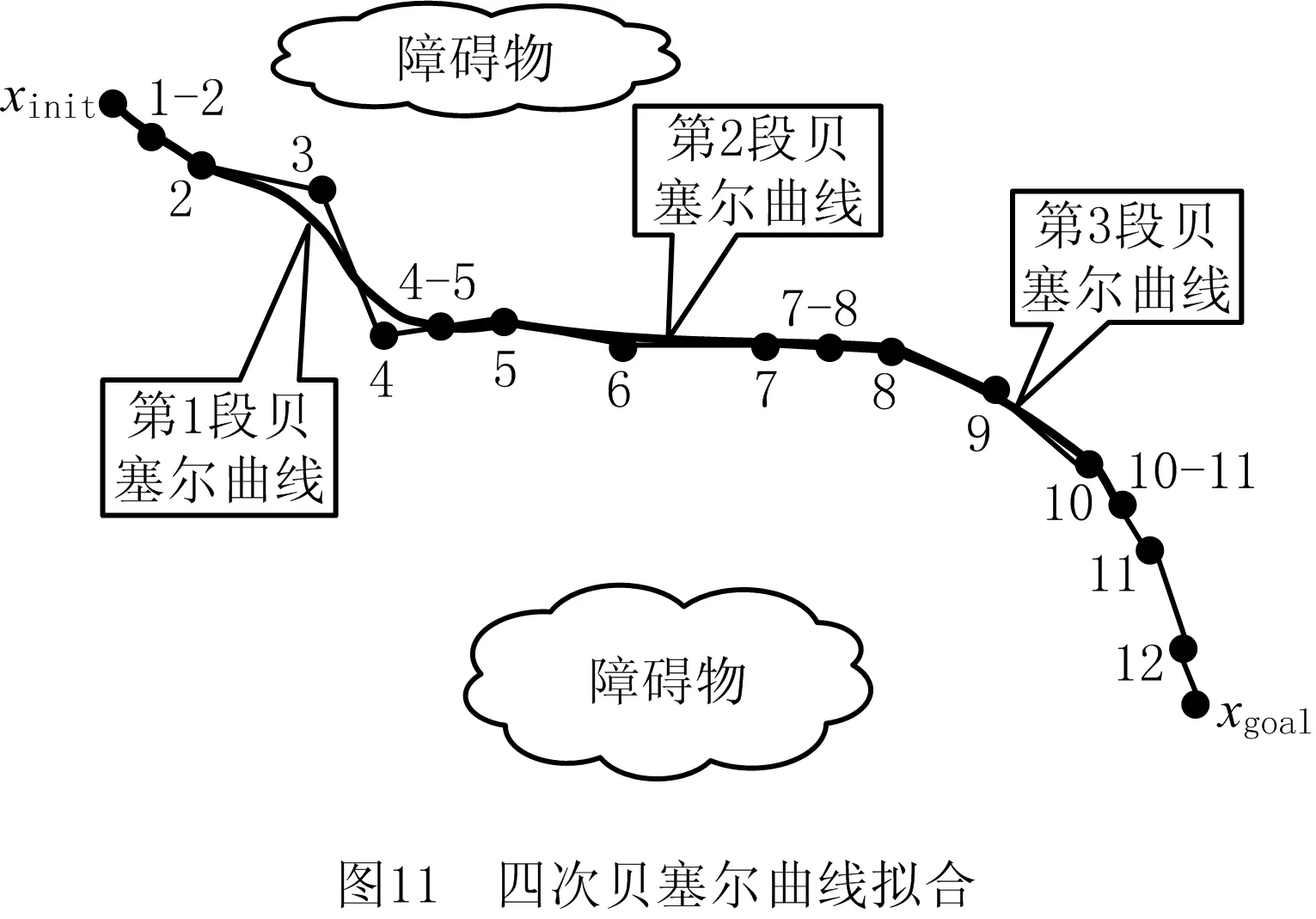
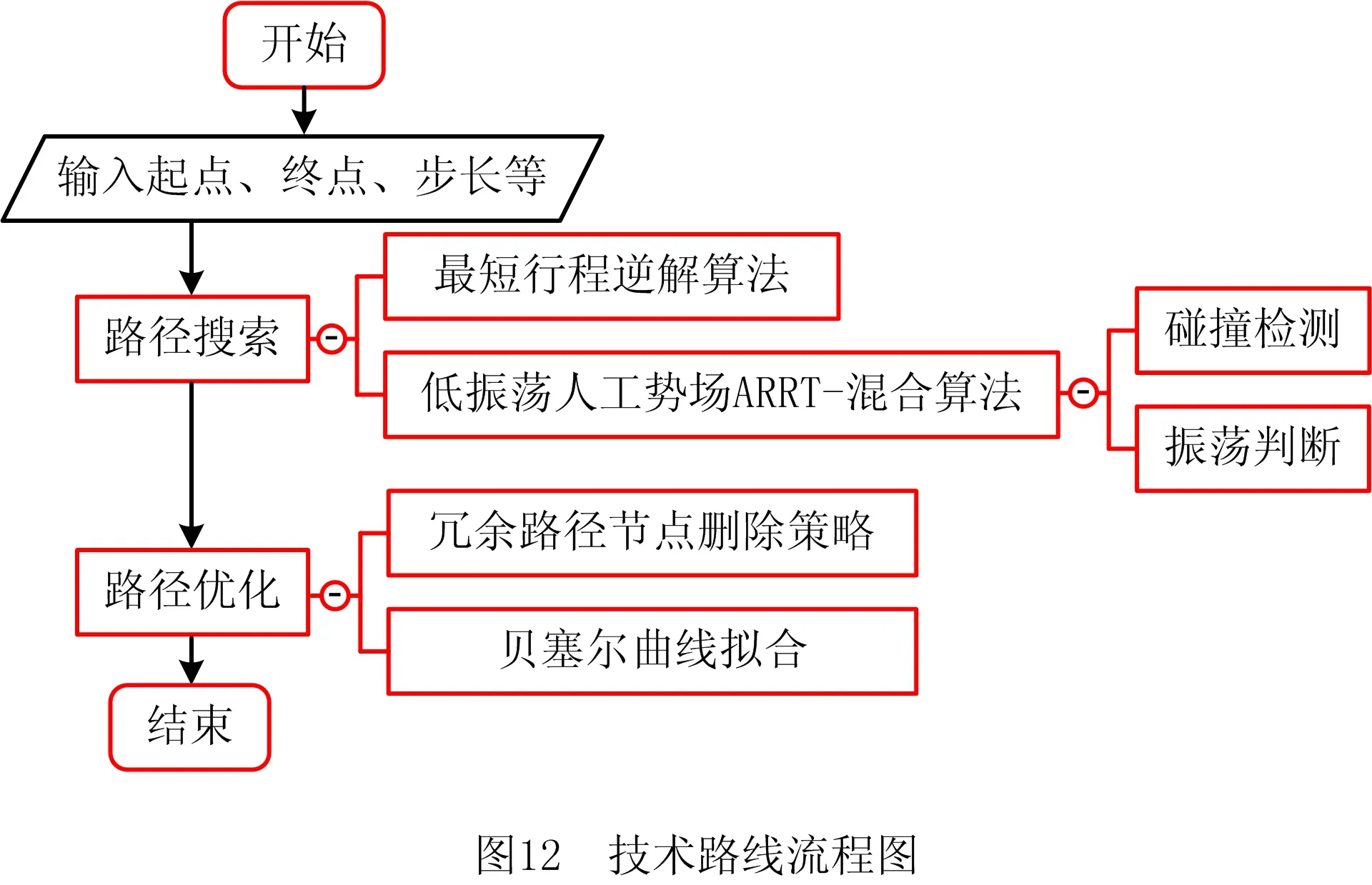
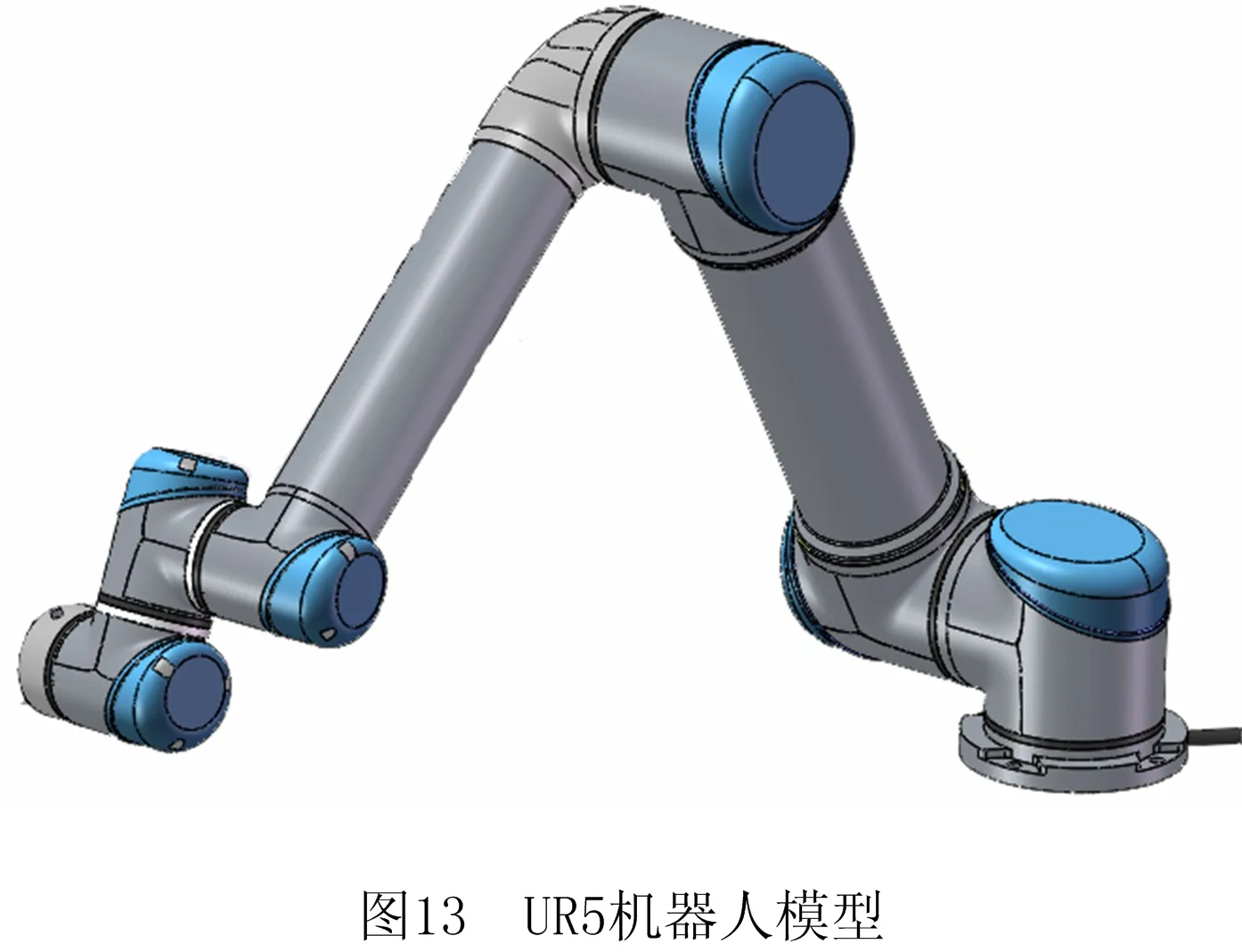
distance (9) 则定义该节点为qinter,并直接连接qnew和qinter,若没有节点和qnew的距离小于一个步长,则直接转步骤(6)。 (5)删除Tree数组和RRTtree数组中qinter和qnew之间的所有节点。 (6)切换回人工势场法。删除振荡中间点,即当前节点qend的前一个节点qend-1。 如图9所示,由节点2、3、4等可判断路径出现振荡,因此删除节点3,并连接节点2和节点4。又因节点4和12之间无碰撞,且距离接近一个步长,连接节点4和12并删除它们之间的节点5、6、7、8、9、10、11。 如图10所示为在低振荡人工势场-ARRT混合算法的基础上使用冗余路径节点删除策略与否的仿真效果对比。在障碍物、步长等其他条件均相同的情况下,使用冗余路径节点删除策略,路径明显得到优化。 2.2.2 四次贝塞尔曲线拟合 为了使得路径在节点转折点处变得光滑,使用四次贝塞尔曲线对路径进行拟合,包含n+1个顶点的n次贝塞尔曲线方程如式(5): (10) 式中:Pi为控制多边形的顶点;Bi,n(t)为伯恩斯坦基函数。 为了降低路径的波动性,但又需要尽量保证拟合的曲线和原轨迹曲线的一致性,选用四次贝塞尔曲线进行拟合,四次贝塞尔曲线最多只能拟合5个点,因此需要使用多段贝塞尔曲线进行拼接,为了保证几何连续性,在起点xinit与节点1中间取过渡点1-2,之后每隔3个节点取1个过渡点,每2个过渡点和它们之间的3个节点共5个点拟合一条四次贝塞尔曲线,以此类推,如图11所示。 已知起点、终点和步长,采用低振荡人工势场-ARRT算法进行搜索,每搜索一个步长,则采用最短行程逆解算法计算机械臂的最优关节角,再进行碰撞检测,规划出一条无碰撞路径之后,采用冗余路径节点删除策略和贝塞尔曲线拟合提高路径质量,如图12所示为技术路线流程图。 为验证算法的有效性,采用丹麦优傲公司的UR5机器人模型作为研究对象,使用MATLAB进行仿真分析。在空间中设置起点和终点,在有限的时间若能规划出一条从起点到终点的无碰撞路径,则避障路径规划成功。该机器人为六自由度机械臂,如图13所示。 如表2所示为机器人的运动控制参数,其中起点和终点根据机器人工作空间范围进行选择,搜索步长和斥力场作用范围根据机器人和障碍物外形尺寸进行设定。 表2 机械臂运动控制参数表 仿真分析1算法对环境复杂程度的适应性实验。 经过4次分析对比,每次相比前一次多增加一个障碍物,模拟环境复杂程度。由图14可以看出,随着障碍物数量增加,低振荡人工势场-ARRT混合算法仍然能够指引机械臂成功避障。 仿真分析2算法搜索效率验证。 在障碍物、步长等其他条件均相同的情况下,比较低振荡人工势场—ARRT混合算法与经典人工势场法、经典RRT算法的路径搜索成功率和搜索时间,实验环境为MATLAB 2016a,计算机处理器为Intel core i3,每组仿真分析均进行20次,结果取平均值,如表3所示。经典人工势场法虽然在障碍物比较少的情况下路径搜索时间短,但是障碍物数量一旦增加,路径搜索成功率低;经典RRT算法搜索时间长,而且随着障碍物数量的增加,其路径搜索成功率降低到60%;低振荡人工势场—ARRT混合算法随着障碍物数量增加,能保证路径搜索成功,满足避障要求,相比于经典RRT算法,在多障碍物环境下的平均路径搜索时间从26.1 s下降到3.6 s,避障路径规划效果得到显著改善。 表3 低振荡人工势场-RRT混合算法路径搜索成功率和搜索时间与经典算法的比较 本文通过分析机械臂在工业生产以及协调作业方面的需求,对机械臂在工作空间中避障的能力进行了研究。在机械臂的正逆运动学的基础上提出了最短行程逆解算法,在经典人工势场法和快速扩展随机树法(RRT)的基础上提出了低振荡人工势场法和自适应快速扩展随机树法(ARRT),并将两种算法结合成低振荡人工势场—ARRT混合算法,完成了对算法在多障碍物环境下的适应能力的提升,提高了算法的搜索成功率和搜索效率。通过仿真分析验证了算法的效果,实现了在多障碍物环境下避障路径搜索,满足避障要求,相比于经典RRT算法,算法在多障碍物环境下的平均路径搜索时间从26.1 s下降到3.6 s,避障路径规划效果得到显著改善。 本文针对机械臂的避障研究基于静态障碍物环境,下一步将针对动态障碍物环境对机械臂的避障算法进行研究,加快算法实时性,在满足机械臂动力学参数的情况下优化路径质量。
2.3 技术路线流程图
3 仿真分析
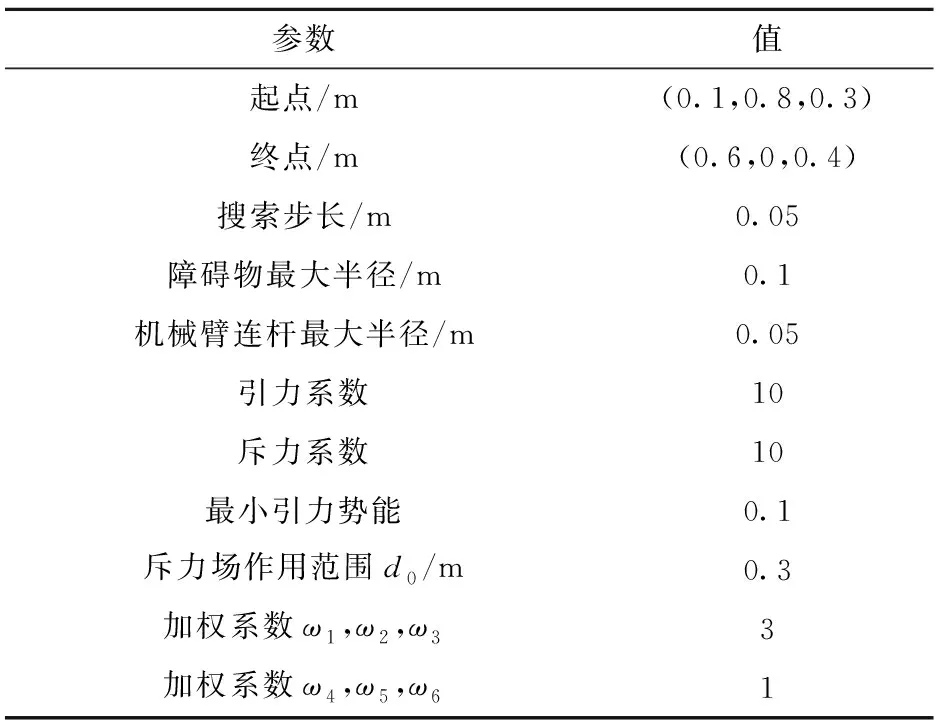
4 结束语

