面向多机器人协调运动规划的层级化任务分配方法
赵文政,刘银华+,金 隼
(1.上海理工大学 机械工程学院,上海 200093;2.上海交通大学 机械与动力工程学院,上海 200240)
0 引言
多机器人光学测量系统以其非接触、可在线等特点在汽车制造领域得到广泛推广,检测系统的路径规划研究也逐渐受到学者们的关注[1]。在实际应用中,多机器人光学检测系统的运动规划需要综合考虑任务分配、机器人路径规划和多机器人协调等问题[2-4],其中在线检测的任务分配是光学测量路径规划的重要环节,也是影响检测周期、多机器人冲突以及测量路径结果的重要因素[5]。
多机器人任务分配问题是典型的混合整数线性规划问题(Mixed Integer Linear Programming, MILP),需要对考虑机器人路径规划和机器人之间协调等条件下的多约束问题进行优化求解。典型的方法有基于MILP模型的求解策略研究[6-7],另外Spensieri等[8]通过建立的MILP模型,利用分支定界的方法实现焊点分配,并搜索得到最优解;Lopes等[9]在MILP模型框架下,考虑机器人参数变换、分布限制、运动时间和机器人干扰约束等因素,对机器人焊接生产线进行任务分配。MILP求解可获得最优解,但其计算资源占用量大,计算效率低,因此不适合大规模问题求解。为了提高求解效率,一些学者利用启发式算法进行任务分配,如遗传算法(genetic algorithm)、拍卖算法模型(auction algorithm)及博弈论(game theory)[10-12]等。进一步,Jones等[13]提出双层拍卖方法解决路径约束的多机器人任务分配问题;Garapati等[14]通过比较博弈论算法找到无人机之间的冲突平衡,并通过投票制度获得最终的分配结果;Zitouni等[15]首先采用萤火虫算法进行全局分配,然后结合量子遗传算法和人工蜂群优化进行局部任务分配;杨煜俊等[16]以最小化完工时间为优化目标,利用领域搜索策略和启发式规则相结合的混合遗传算法求解作业车间内多机器人制造单元调度问题;张则强等[17]针对装配线平衡问题的具体特点,综合考虑装配作业时间和后续任务数的分级位置权重,通过改进蚁群算法进行装配线平衡问题求解。
上述算法可实现多机在规定时间内的任务均衡分配。但随着任务数目增加,以上方法存在计算量指数增加的问题。为此,学者们提出对任务集进行聚类分析[18-20],并对聚类后的簇进行多机分配以达到降低计算量。如早期研究中,Elango等[21]首先基于K-means和最小距离对任务集进行聚类,然后计算每个机器人与聚类集群所组成集合的成本,最终根据拍卖算法进行任务分配;Janati等[22]利用K-means算法将任务划分为机器人的数量,利用线性分配将机器人分配给任务集。
从上述研究可以看出,已有任务分配方法主要适用于单层次任务分配问题,即任务到多机器人的分配。而在车身在线检测(生产节拍为60~90 s)过程中,需要将数百甚至上千个检测任务同时分配到多机器人、多批次车身,以实现有限检测周期内车身特征的全检,同时满足多机器人动态环境下的协调运动等需求。面对大量检测任务到多批次车身、多机器人的分配问题,当机器人数目、车次数目一定时,潜在的任务分配方案的数目与待分配任务数目之间呈指数关系,且每次候选分配方案均涉及机器人运动学与路径规划的优化求解。因此,本文提出层级化测量任务分配(Hierarchical Inspection Task Allocation, HITA)算法,通过将待测任务集的初步分配、模糊聚类以及面向多机协调的多目标优化的细化分配,实现检测任务的高效分配,降低算法复杂度(具体分析见2.2节),提升在线检测效率。
1 车身光学在线检测的任务分配问题
在汽车车身装配生产线中,光学在线检测(如图1)是实现车身质量100%测量的重要手段。考虑到车身大型曲面结构,需通过多台搭载光学传感器的机器人对车身特征(如孔、槽、曲面、边缘、螺纹等)进行非接触和在线测量。图2所示为多机器人光学在线检测过程,其中BIW(body in white)表示白车身。由于在线生产节拍的限制,多机器人工位无法从单一车身上采集到所有关键特征的信息。这就要求将任务集分配给同一批次内连续m个车次进行检测,每台车身分配到的任务子集互不相交且各子集之和为任务全集。另一方面,针对确定的车次,需将检测任务分配给工位内不同机器人,并要求多机器人系统无干涉协调运动,且满足工位内检测周期、多机运行时间一致性等要求。


本文的目的是将检测任务分配到不同检测车次内的各机器人,使得每个机器人所分配的任务量的检测时间尽可能短且满足生产节拍限制等约束。结合上述问题描述,本文层次化任务分配过程进行如下假设:
(1)多层次任务分配时,待分配车次的数目为提前预设;
(2)各待测特征的光学最佳测量参数(如入射角、景深等)及公差已知;
(3)车身检测过程各机器人的起始测量时间相同;
(4)针对不同类型的待测特征,其光学检测时间相同,即机器人到达测量位置后的测量时间相同;
(5)机器人完成单车次任务检测后均返回其初始位置。
基于上述假设,本文的在线检测多任务分配模型可表达为:
minTi(Ri),Ri={Ri1,Ri2,…,Rin},Ri∈R。
(1)
s.t.
Ti (2) ΔTi<ε; (3) R11∩R12∩…∩Rmn-1∩Rmn=∅; (4) R11∪R12∪…∪Rmn-1∪Rmn=R。 (5) 其中各符号的含义如下: n为检测工位内机器人总数; m为批次内车次总数; Rij为第i个车次第j个机器人分配的任务集,i={1,2,…,m},j={1,2,…,n}; Ri为批次内第i个车次下各个机器人候选任务集; R为检测任务全集; Ti为第i车次的实际检测周期; T0为在线检测工位的生产节拍; ΔTi为第i个车次内n个机器人中检测时间的极差; Tij为第i个车次第j个机器人的检测时间; ε为最大的运行时间极差阈值。 第i个车次第j个机器人在给定任务集下检测时间的计算公式可表示为: (6) (7) (8) 其中:t01、tM0为分别表示从机器人运动路径中初始位置到首个待测特征和最终待测特征返回机器人初始位置的机器人运动时间;xpq为0,1变量;tpq为给定车次下某机器人从特征Fp移动到特征Fq的运动时间; 为了提高在线检测效率,本文采用层级化方法对该分配问题进行启发式求解,具体流程为:首先基于懒惰旅行商问题的求解策略,将检测共享空间内的检测特征分配给不同机器人,实现检测任务全集到多机器人的初步分配。然后,针对上述机器人分配到的任务集,采用模糊C-Means(Fuzzy C-means, FCM)算法进行聚类分析,获得与检测工位机器人数目相同的任务簇。最后,提出考虑任务簇中心和单机运动时间等多目标的任务分配优化模型,实现测量任务到具体车次、机器人的细化分配。 通常,搭载光学测头的六轴机器人左右对称分布于在线检测工位,车身尺寸特征通常会落在一个或多个机器人可达范围内。当检测特征落在多机器人共享空间内时,需将其分配给某个确定的机器人。传统基于距离的分配方法将导致每个车次下多机器人检测时间的极差增大,从而导致检测效率不高。因此,为了保证每个车次机器人工作时间的一致性,本文在设置每个机器人所分配检测特征数目约束的条件下,利用懒惰旅行商问题(lazy Traveling Salesman Problem, lazy TSP)的求解策略,将共享空间内的检测特征粗分配到每个机器人。具体共享空间内检测任务的分配策略如下: (1)根据机器人可达性计算得到多个机器人共享空间内的检测特征集合,如第j个和第j+1个机器人共享空间内检测特征集合为Uj,j+1。以Uj,j+1内的特征为例,说明提出算法的分配过程。 (2)根据检测特征的总数目以及机器人的数目,设置单机器人最大检测特征数目的阈值为φ。 (5)若同时满足Lj (6)重复步骤(3)~步骤(5)直到Uj,j+1内的特征分配完成。 基于上述分配算法,即可得到每个机器人分配的特征任务集R1,R2,…,Rn。具体分配过程的伪代码如下: imax=sizeof(Uj,j+1);%imax表示Uj,j+1内集合的数目; for i=1:imax if Lj elseif Lj end end 对检测任务粗分配后,需进一步将其细分给批次内不同车次下的多个检测机器人。传统将路径距离或检测时间作为目标函数的MILP模型的任务分配方法,往往忽略多机器人分配任务集之间的关系,导致多机协调阶段机器人发生冲突甚至停机的现象,从而降低了检测效率。为解决该问题,本文基于聚类算法将第j个机器人的粗分任务集Rj划分成m类。然后,根据式(6)计算机器人无碰检测路径的最短时间。进一步,考虑批次内多车次下机器人的检测时间一致性,以及多车次下相邻机器人任务集的聚类中心间距离,构建任务细化分配的多目标优化模型,并利用改进的模拟退火(Simulated Annealing, SA)算法进行求解,获得不同车次内多机器人的任务分配结果。 传统K-means聚类是一种将每个任务对象非此即彼地严格分类的聚类算法。然而,在多机器人检测工位中,对于检测任务集内的部分测量任务可以由多个车次内多个机器人检测,即并非严格的“0-1”关系,若利用K-means进行聚类,将很难得到较为明显的簇,且由于车身检测特征分布差异较大,致使各个簇内元素较为分散,优化分配后会增加各车次内的机器人运行时间增加,降低检测效率。FCM算法作为一种无监督聚类算法,利用模糊理论对重要数据进行分析和建模,使得被划分到同一簇的任务之间相似度较大,而不同簇之间的相似度较小。因此,FCM能通过优化每个检测任务的隶属度获得较为明显的聚类效果,使得簇内元素分布较为集中,从而为后续分配优化提供基础。 综上所述,本文基于FCM算法对任务集Rj进行聚类,具体过程为:设第j个机器人的任务集为Rj={F1,F2,…,FN},其中N为Rj内测点数量,F为Rj内的测点;通过迭代的方法将任务集Rj分解为m个子集Cij(i=1,2,…,m,j=1,2,…,n),并根据隶属度计算每个子集聚类中心vij(i=1,2,…,m)。因此,基于FCM算法求解,可将2.1节中每个机器人分配到的检测任务集Rj分解成n×m个子集。 在上述任务集聚类基础上,为了缩短机器人之间的运行时间差,同时减少机器人之间发生冲突的概率,本文以SA算法对不同车次、多机器人检测任务进行优化分配,算法流程如图3所示。 具体算法流程如下: (2)基于上述计算得到的每个车次内机器人检测时间Tij及产生的新解W,计算各车次内检测时间的极差值ΔTi。其中单车次下机器人检测时间的计算方法如下:针对给定的机器人检测任务,本文采用几何避障算法对机器人初步分配得到的测点集Cij内的两两检测特征的局部无碰撞路径进行优化,建立两两检测测点之间的无碰撞运动时间矩阵[23-24]。同时,为了保证单机器人检测时间最优,将问题转换为寻找时间最短的无碰撞路径的TSP。对于TSP,可通过SA、GA以及分支定界等算法进行求解,最终得到每个机器人对不同测点集Cij的检测时间Tij。 (3)以ΔTi和相邻两机器人(若两机器人之间存在检测共享空间,即为两机器人相邻)所分配的任务集Cij的聚类中心vij之间距离建立SA算法的加权多目标函数: (9) (4)通过不同行内元素相互交换产生新解W′(如图4),计算ΔF=F(W′)-F(W)。 (5)计算ΔF,并判断其是否小于零,若ΔF<0,则接受W′为新的当前解;若ΔF>0,则以一定概率接受为新解。 (6)判断W′是否满足迭代终止条件,满足则输出多车次、多机器人任务分配结果;否则,添加扰动产生新解,并返回步骤(2)。 基于上述改进SA算法对聚类后的测点集进行多目标优化,即可求解得到不同车次内满足节拍周期T0分配结果。本文以每个工位内相邻机器人测量任务集的聚类中心之间的距离为优化参数,当相邻两机器人之间的聚类中心差值越大时,则所建立的目标函数F越小,使得相邻机器人检测任务集在空间位置中得到分离,减少机器人检测任务集之间相互“交叉”的现象,从而降低了机器人间发生碰撞的概率。 为进一步减少机器人在运行过程中由于潜在冲突造成的时间损耗,本文通过解耦法实现多机器人协调运动。第一阶段采用几何法避障[23-24]实现每个机器人两两检测任务在静态环境中的局部无碰撞路径规划,建立检测任务之间无碰撞时间矩阵,从而将单机器人路径优化问题抽象为TSP问题,通过优化序列完成路径优化;第二阶段以各机器人完成检测任务的周期时间最短为优化目标,采用动态优先级的策略实现多机器人在碰撞状态空间的协调优化[25]。 从算法的时间复杂度上看,以基于模拟退火算法的单层次任务分配算法为例,其任务分配的时间复杂度约为O((log(Qmin/Q)L)2R0N)。其中:Q为模拟退火算法的初始温度;Qmin为模拟退火算法的温度下限;L为每次得到的Q值下算法的迭代次数;R0为各工位、各机器人中分配任务数目的最大值;N为待分配任务数目。而基于所提出HITA算法的时间复杂度约为O((log(Qmin/Q)L)2R0)。因此,所提出的HITA算法可有效地降低多车次多机器人检测任务分配的算法复杂度,提高在线检测任务分配问题的求解效率。 结合某整车制造企业在线检测工位对所提方法进行应用,该车型待测特征数目为200,其检测测点位置与矢量方向如图5所示。该检测工位布置有4个搭载有光学测头的工业机器人,型号为FANUC 2000iB-125L,在批次内拟对4个车次白车身进行全特征检测,在线检测工位检测时间阈值T0=45 s。为了验证所提方法的有效性,本文引入目前广泛应用的就近原则和基于SA算法的求解方法[11,26](以下称为对比方法)与本文提出的HITA方法进行对比,通过提取各车次检测周期、工位内多机运动时间差等指标对各方法的有效性进行验证。 基于就近原则分配到各检测机器人的任务集R1、R2、R3和R4中测点数目分别为63、36、46和55。进一步基于SA退火算法[26]对不同车次内多机器人的检测任务进行优化分配,获得最终的检测任务细化分配结果如图6所示。 根据本文提出的层次化任务分配算法,各检测机器人的任务集R1、R2、R3和R4中测点数目分别为48、52、49和51,如图7所示。 进一步,利用FCM聚类算法对上述机器人的检测任务集Rj进行聚类,并划分为4个簇。同时,考虑机器人与车身之间的碰撞检测规避,计算每个任务簇内单机无碰撞检测路径所需运行时间。然后,利用提出的改进SA算法将机器人检测任务集的每个簇进行组合优化分配给各个车次。其中,需考虑不同任务簇组合时机器人的动态碰撞规避,并根据碰撞情况更新各簇内检测路径所需运行时间,分配结果需满足检测周期,即T0<45 s,同时尽可能减少多机运行时间差ΔT。如图8所示为基于所提出的HITA方法给出的各车次任务分配结果。 基于上述两类方法的任务分配结果,计算各车次在检测工位内各机器人的检测时间并进行对比分析。如表1所示为不同任务分配方法下的多机器人工位检测时间。如图9所示为不同车次在多机器人测量工位的检测周期T0与多机最大运行时间差ΔT。 表1 不同任务分配方法下的多机器人工位检测时间对比 s 从图6和图8的测点集位置图可见,对比方法得到每个车次的各机器人所分配测点在空间位置中出现相互”交叉”的现象,如图6中方框内测点,这将增大多机器人在运行过程的干涉可能性。而基于HITA算法得到的每个机器人分配测点集在空间位置上尽可能相互独立,减少了多机器人运行过程中的干涉可能。这种相互分离的分配策略虽然存在延长机器人运行时间的可能性,但将有效降低机器人间协调规划成本。 从任务分配结果的检测时间上看,图9显示两种方法得到各机器人在不同车次的检测周期在34~44 s。基于对比方法,得到不同车次检测周期平均为41.17 s,基于HITA算法的平均检测周期为37.84 s,减少3.33 s,这将为在线测量中的测点数目增加提供条件。另外,针对多机运行时间的一致性,本文将各车次的多机最大运行时间差的平均值降低5.25 s,有效提升了多车次内各机器人运行时间的均衡性。因此,本文所提算法在既定检测任务下,可保证工位内多机器人检测时间的一致性,同时可有效提高检测工位内多机器人工作效率,更好地保证车身精度的在线测量需求。 本文提出一种在线光学检测系统层级化任务分配方法,包括机器人间特征分配、面向车次的特征聚类及任务集组合优化分配求解等步骤。通过基于欧式距离的惰性旅行商问题求解确定了各机器人的检测特征任务集,为后续进行车次间任务分配提供了基础。通过FCM算法对机器人获得的检测任务集进行聚类,并利用改进的SA算法将各任务簇细化分配给不同车次,在保证生产节拍、多机运行时间差等多约束下,提升了车身在线检测效率。通过案例分析,验证了本文算法对在线检测过程中任务分配问题求解的有效性,也将为多机器人检测系统的运动规划仿真软件开发提供算法基础。2 层次化检测任务分配
2.1 检测任务到机器人系统的粗分配



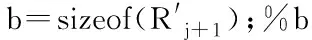


2.2 针对不同车次下多机器人的细化分配




3 案例分析







4 结束语

