改进的球头铣刀加工表面形貌建模方法

王仁伟，张 松+，葛人杰，栾晓娜，王家昌，鲁韶磊

(1.山东大学 机械工程学院高效洁净机械制造教育部重点实验室，山东 济南 250061；2.山东大学 机械工程国家级实验教学示范中心，山东 济南 250061；3.青岛海信模具有限公司，山东 青岛 266114)

0 引言

为了满足流体力学等功能性需求及人们日益增长的审美需求，复杂曲面结构被广泛应用于航空航天、天文、航海、汽车零部件、模具和生物医用植入等领域的众多工业产品及零件的重要工作面。球头铣刀具有几何自适应性好、轨迹规划算法简单、干涉易于检测等优点，常用于复杂曲面的数控加工[1]。表面形貌是表面完整性的重要内容，对零件的耐磨性、抗腐蚀性和密封性等诸多性能具有重要的影响[2]。因此，分析球头铣刀加工表面形貌的形成机理，对改善复杂曲面零部件的加工表面质量、提高服役性能具有重要的研究意义及工程价值。

与实验研究相比，理论建模方法易于揭示铣削表面形成机理、便于研究单一因素对表面形貌的影响，因此铣削表面形貌建模研究受到了极大关注[3]。Yang等[4]建立了变齿距铣刀加工表面形貌仿真模型，并分析了切削参数、刀具跳动、刀具螺旋角等对表面粗糙度的影响;Arizmendi等[5]对利用球头铣刀制备表面微凹坑的过程进行仿真，并分析了刀具倾角、切削参数等对凹坑尺寸及的影响，为改善表面间的摩擦性能提供了参考;Zhao等[6]利用几何建模与神经网络相结合的方法，建立了球头铣刀加工表面形貌的多尺度预测模型;Peng等[7]分析了刀具初始相位角对球头铣刀微细加工表面形貌的影响，并通过规划刀具路径实现了刀具初始相位角及加工表面形貌的控制;Zhang等[8]分析了进给量和铣削宽度对球头铣刀加工表面粗糙度及材料去除效率的影响，并在给定材料去除效率的限制下，通过合理选择切削参数获得了理想的加工表面粗糙度;Wang等[9]分析了薄壁零件切削加工中，切削振动对表面形貌及粗糙度的影响;Xu等[10]建立了考虑机床动态进给速率的表面形貌仿真模型，提高了复杂刀具路径时表面形貌预测精度;Zhang等[11]和Li等[12]利用迭代方法计算刀刃扫掠面与工件网格参考线交点，进而改善了表面形貌模型的预测精度。综上所述，基于时间步长控制的铣削表面形貌仿真算法，通过在单个切削时间步上预测工件离散网格点的表面形貌值，有利于综合考虑多种因素对表面形貌的影响，具有极强的扩展能力。

然而，为了保证模型的稳定性和预测精度，在传统时间步形貌模型中，需要严格限制刀刃微元尺寸及切削时间离散步长，即保证刀刃微元在单个切削时间离散步至多扫掠一个工件网格点，增加了模型的数据量及计算时间，降低了模型的计算效率。相比于离散点云模型而言，三角形网格模型能够更好地表达刀刃扫掠面的几何特征，已被成功地用于球头铣刀铣削加工仿真的刀刃切削状态识别[13]和未变形切屑厚度计算[14]。

本文将三角形划分引入基于时间步长控制表面形貌模型中，提出一种改进的时间步形貌模型。基于不同刀具倾斜角时刀具与工件接触关系，建立了切入刀刃模型，同时基于单个切削时间步刀刃微元扫掠面的三角形网格模型，提出了面向扫掠面三角形网格与过工件网格点竖直参考线相交的铣削表面形貌仿真方法。最后，利用AISI P20钢球头铣刀加工实验，验证了改进时间步形貌模型的有效性，并与传统时间步形貌相比较，验证了改进时间步形貌模型的性能的优异性。

1 表面形貌建模

1.1 球头铣刀刀刃方程

(1)

式中：R为刀具半径，(单位：mm)；κ为点P与球心连线与刀具轴线的夹角，即轴向位置角，(单位：rad)；φ为点P在XjYj平面上的投影P′与Oj的连线与Xj轴的夹角，即螺旋角，(单位：rad)。对于等导程铣刀而言，螺旋角φ可表示为如式(2)所示的关于轴向位置角κ的函数[15]：

φ=tanβ0-tanβ0·cosκ。

(2)

式中β0为名义螺旋角，在底刃与侧刃交点处测量。

(3)

式中φj为Xj轴与XT轴的夹角，(单位：rad)。对于刀刃数nf的等齿距铣刀而言，φj可以表示为如式(4)所示的关于刀刃数的函数：

(4)

1.2 刀刃扫掠面方程

(5)

式中：α为刀具绕主轴轴线转过的角度，α=ω·t+α0，(单位：rad)；ω为主轴旋转角速度，(单位：rad/s)；t为切削加工时间，(单位：s)；α0为初始加工时刻XS轴与XT轴的夹角，即刀具初始相位角，(单位：rad)。

(6)

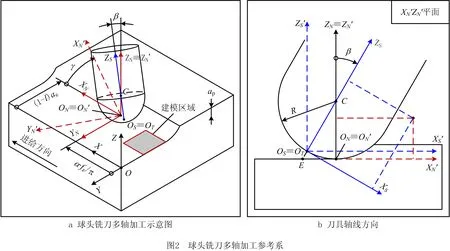
为描述刀具与工件之间的相对运动关系，建立如图2a所示的工件坐标系O-XYZ：其原点O位于设计表面上，Z轴沿着设计表面的法线方向；X轴沿着刀具进给方向；Y轴分别垂直于X轴和Z轴，并构成右手笛卡尔坐标系。因此，对于刀触点坐标系

在投融资方案上充分发挥政府投资对社会资本的引导放大作用，吸引社会资本参与。要坚持以市场为导向，以制度建设为重点，形成市场融资为主导、政府投资为补充、民间投资健康发展的投融资格局。在旅游、医疗、教育、停车等社会化产业服务领域，坚持以政策导向引领，社会资本主导参与建设为原则，通过出让特许经营权、第三方付费、使用者付费结合少量政府补助的方式，鼓励社会资本加大此类应用的建设力度和速度。利用社会资本的灵活性和企业服务的创新性实现智慧城市的长期可持续发展。

(7)

式中：nf为铣刀刃数；fz为每齿进给量(单位：mm/tooth)；l为刀具路径编号；ae为铣削宽度(单位：mm)。

联立式(1)～式(7)，可得工件坐标系下的刃刃扫掠面方程为

(8)

式中：TNW、TSN、TTS、TjT为坐标转换矩阵。

1.3 铣削表面形貌仿真算法

铣削加工中刀刃断续去除工件材料形成表面材料残留，并形成最终的铣削表面形貌，因此加工表面的残留高度由刀刃扫掠面与工件交点的最低值决定。因此，通过求解出工件在采样点处与刀刃扫掠面的最低交点，可实现铣削表面形貌的仿真，具体表面形貌仿真步骤如下：

(1)如图3所示，利用Z-map方法将工件的待加工表面划分为m×n个正方形网格，网格间距为dw。将工件表面各个网格点的Z坐标值保存在一个二维数组H中，铣削仿真开始前，设置每个网格的Z坐标值均为轴向切削深度ap。

(2)如图4所示，给定球头铣刀半径R、铣削深度ap、倾斜角β，分别按式(9)和式(10)求出参与切削刀刃的最小轴向位置角κ1及最大轴向位置角κ2。按照等弧长原则将切入刀刃离散为nce个刀刃微元[16]。

κ1=

(9)

κ2=β+arccos(1-ap/R)。

(10)

(4)利用文献[12]中的方法搜索落入三角形网格在XY平面投影中的工件网格点，并计算通过该网格点的竖直参考线与扫掠面近似三角形网格的交点(如图5)[17]，保留交点高度与工件网格原始高度之间的最小值(即Z坐标值)作为工件网格点的表面形貌值。

(5)对应每个刀齿上的刀刃微元重复步骤(3)和步骤(4)。

(6)最终，基于矩阵H中所保存的工件表面网格点的高度值，绘制表面形貌及计算表面粗糙度。

按照如图6所示算法流程，利用MATLAB 2020a软件编写铣削表面形貌仿真程序，绘制铣削表面形貌图及计算表面粗糙度值。仿真用计算机配置如下：处理器i5-10400@2.9 GHz，内存8 GB DDR4。

2 验证实验

为验证改进形貌模型的有效性，参考刀具样本、模具实际加工及已发表文献[18-19]，设计了加工参数如表1所示的切削实验。球头铣刀加工实验在5轴立式加工中心(DMU60P，德玛吉)上进行，采取干式切削加工方式，以避免使用切削液带来的能源消耗。工件材料为切削加工性能较好的预硬塑料模具钢AISI P20，其化学成分和材料属性如表2和表3所示。刀具选择整体式球头立铣刀(970100-TRIBON，山高)，刀具齿数为2，半径为5 mm，螺旋角为30°，刀具悬伸长度为25 mm。

表1 切削实验加工参数

表2 P20塑料模具钢化学成分(wt%)

表3 P20塑料模具钢材料属性

铣削完成后，采用超声清洗去除已加工表面杂质。在加工表面稳定切削区域均匀布置3个采样区域(1.5 mm×1.5 mm)，利用光学轮廓仪(WYKO NT9300)测量已加工表面高度坐标，利用式(11)计算加工表面粗糙度[20]：

(11)

式中：M为在采样区域内沿着X轴方向的采样点数目，N为在采样区域内沿着Y轴方向采样点数目，M与N均等于1 537;Zmn为采样点与平均平面之间的距离。

3 结果分析

3.1 模型稳定性分析

如图7a所示，当刀刃微元尺寸ΔS从0.02 mm增加到0.12 mm时，表面粗糙度预测值基本不变，表明当刀刃微元尺寸小于0.12 mm时，改进表面形貌模型处于稳定状态，具有较为可靠的预测能力。当刀刃微元尺寸大于0.12 mm，表面粗糙度预测值出现波动，且随着刀刃微元尺寸的增加，波动范围逐渐变大，表明刀刃微元尺寸大于0.12 mm时，改进表面形貌模型处于不稳定状态，不再具有可靠的预测能力。在改进表面形貌模型处于稳定状态时，程序运行时间随着刀刃微元尺寸的增加而降低，并且降低速率逐渐变小。如图7b所示，切削时间离散步长对模型稳定性与计算效率的影响与刀刃微元尺寸影响类似。由图7可知，模型处于稳定状态时的刀刃微元尺寸(0.02 mm～0.12 mm)及刀刃微元单个切削时间步轨迹长度(0.02～0.6 mm)均大于工件网格尺寸(0.02 mm)，表明改进时间步形貌模型突破了工件网格尺寸对刀刃微元尺寸及切削时间离散步长的限制。

3.2 模型预测精度及计算效率分析

铣削表面沿进给方向存在5个材料残留，且相邻两个材料之间的距离与每齿进给量相等(如图8a)；铣削表面沿垂直进给方向存在6个材料残留，且相邻两个材料残留之间的距离与铣削宽度相等。因存在刀具初始相位角α0，使得相邻刀具路径上的材料残留沿着进给方向发生偏移。实验测量及仿真铣削加工表面的材料残留分布基本一致，表明形貌仿真模型能够较为准确地预测铣削表面材料残留。

4 结束语

本文基于建立的刀刃扫掠面三角形网格模型，提出了改进的面向时间步控制的铣削表面形貌仿真模型。分析了刀刃微元尺寸及切削时间离散步长对模型稳定性及计算效率的影响，并对比形貌仿真与实验测量得到的球头铣刀加工表面形貌及粗糙度结果，获得主要以下结论：

(1)在工件网格dw=0.02 mm时，刀刃微元尺寸处于0.02 mm～0.12 mm范围内、刀刃微元单个时间步轨迹长度处于0.02 mm～0.6 mm范围内，改进的时间步形貌模型表面粗糙度预测值均收敛，表明其突破了传统时间步形貌模型工件网格尺寸对刀刃微元尺寸及切削时间离散步长的限制。

(2)改进时间步形貌模型预测表面与实验测量表面上的材料残留物数量及分布具有良好的一致性，且表面粗糙度结果偏差在15%以内，表明改进的时间步形貌能够有效地预测球头铣刀加工表面形貌和粗糙度值。

(3)通过对比分析利用传统时间步形貌模型与改进时间形貌模型所预测的表面粗糙度预测值及程序运行时间，发现改进的时间步形貌模型具有更高的预测精度及计算效率。

为改善复杂曲面球头铣刀加工表面质量，降低表面粗糙度，下一步将利用提出的改进形貌模型进行复杂曲面加工过程中表面形貌和粗糙度预测，以及切削参数优化。