CL-20 热膨胀和相变的ReaxFF-lg 分子动力学模拟

李昌霖，甘 强，冯长根，胡靖伟，朱双飞，程年寿

（北京理工大学爆炸科学与技术国家重点实验室，北京 100081）

1 引言

笼形多硝基化合物六硝基六氮杂异伍兹烷（简称HNIW 或CL-20）［1］是已应用能量最高的单质炸药，由于分子中硝基空间取向和晶格堆积方式不同，常温常压下CL-20 主要存在α、β、γ 和ε 四种晶型，其中ε 晶型密度最大。在极端条件下CL-20 可发生复杂相变反应，导致密度减小或内部缺陷产生，影响其爆轰性能和安全性。实验研究表明，β-CL-20 在高温和高压下发生β→ε 和β→α 相变，γ-CL-20 可由β-和γ-CL-20 转化而成［2］，高温下发生ε→γ［3-5］和α→γ 相变［6］，高压下存在ε→γ［7-8］相变。由于升温速率等实验条件不同，已报道CL-20 相变温度存在一定差异，且实验方法一般只能适用于CL-20 两相体系相变分析，难以考察晶体中分子微观变化。2016 年张力［9］采用分子动力学方法和凝聚态优化分子力场（COMPASS）计算表明，ε-和β-CL-20 相变温度分别为450 K 和490 K，略高于实验值［10］。

2001 年，van Duin 等［11］首次在分子动力学模拟方法中引入键级概念，提出针对碳氢化合物的反应性力场（Reactive Force Field，ReaxFF），2011 年Liu 等［12］对该力场的长程色散作用进行低梯度校正，提出适用于含能材料的ReaxFF-lg 力场，对黑索今（RDX）、奥克托今（HMX）等含能材料计算晶胞参数误差≤1%，已应用于HMX 的热膨胀和相变研究［13］，尚未应用于CL-20高 温 相 变 分析。Wang 等［14］采用ReaxFF-lg 力 场 研 究了ε-CL-20 热分解机理，但常态下计算密度只有1.921 g·cm-3，与实验值（2.035 g·cm-3）［15］偏差较大；Ren等［16］采用ReaxFF-lg力场研究β-CL-20热分解机理，计算密 度 为1.938 g·cm-3，也与实 验 值（1.989 g·cm-3）［17］有一定偏差。

本研究对ReaxFF-lg 力场的价角势能截距进行了修正，计算了ε-、β-和γ-CL-20 的晶胞参数、晶格能和升华焓，采用Birch-Murnaghan 固体状态方程拟合了ε-CL-20 的p-V 状态曲线，验证力场适用性。通过晶胞参数、晶体结构变化考察了ε-、β-和γ-CL-20 高温相变过程，分析CL-20 热膨胀规律。

2 实验部分

2.1 ReaxFF-lg 力场表达式及价角势能修正

采用ReaxFF-lg 力场开展分子动力学模拟，其系统总能量由下列价键作用组成［11-12］：

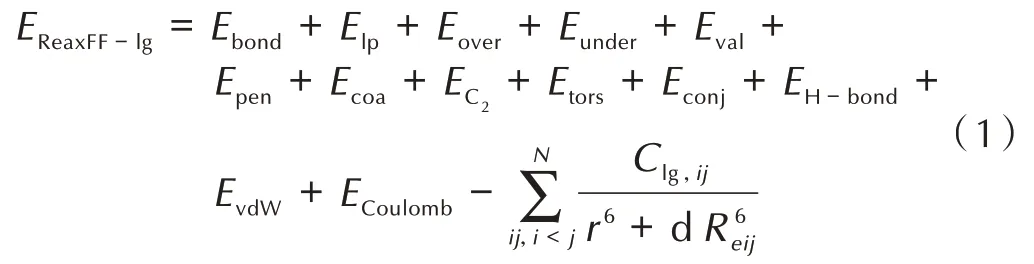
式中Elp、Eover、Eunder为原子本身贡献，Ebond、EC2为双原子体系贡献，Eval、Epen、Ecoa为三原子体系贡献，Etors、Econj为四原子体系贡献，EH-bond为氢键贡献，EvdW、ECoulomb为非价键作用力，kJ。价角能Eangle是Eval的主要组成部分，力场将单原子与两键认作键角体系，由两键的键级BOa、BOb与两键所成角度θ 来表达价角能的值，价角能Eangle表达式为：

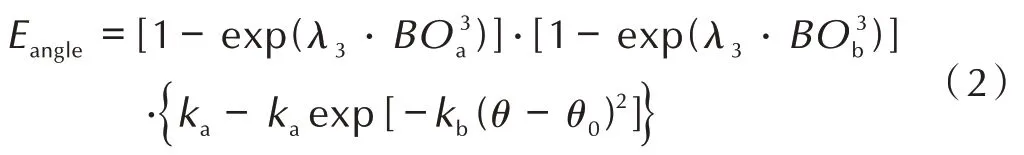
式中，λ3为力场参数决定的价角参数；ka为特定角的首要力常数；BOa、BOb为两键键级；θ 为键角角度，θ0价角的平衡角度，单位为（°）。当组成此角的两键中的任意一键键级小于此截距时，反应力场便会忽略此角，其缺省值为10-3。该力场中存在键级为10-3～10-2的弱键存在于同分子的两端或不同分子之间，影响低梯度范德华力的表达。所以控制价角的键级截距，可消除这部分弱键对体系能量影响，提升该实验方法的准确度。

2.2 模型建立与晶格参数分析

模拟计算采用大规模原子分子并行模拟程序（Large-scale Atomic/Molecular Massively Parallel Simulator，LAMMPS）［18］。从剑桥晶体数据中心提取ε-CL-20［15］、β-CL-20［19］与γ-CL-20［20］晶体数据，初始单胞内均含有4 个分子，共144 个原子。

对初始单胞三个方向分别进行3 倍、3 倍、2 倍的周期性扩增，构建包含72 个CL-20 分子，共2592 原子的ε-、β-和γ-CL-20 超晶胞，并将力场的价角能截距由缺省值10-3修改为10-2。采用Polak-Ribiere 共轭梯度算法［21］将各晶型CL-20 超晶胞进行能量最小化，收敛精度为4.19×10-6（kJ·mol-1）·Å-1，获得0K 时的优化后的原子位置。随后采用Maxwell-Boltzmann 随机分布，给予各体系内每个原子一个随机初始速度。在正则（Canonical Ensemble，NVT）系综下弛豫10 ps 后，在298 K 和0 GPa 条件下，使用等温等压（Isobaric-Isohermal Enermble，NPT）系综弛豫100 ps，得到充分弛豫后结构。NVT 与NPT 系综所依据的运动方程均为结 合Martyna 静 水 力 学 方 程［22］与Parrinello-Rahman应变能方程［23］的Shinoda 运动方程［24］，并遵循Tuckerman 时间积分方案［25］。以上弛豫过程中时间步长均为0.1 fs，每一步生成一次原子近邻列表，取最后10 ps的数据进行统计分析，绘制密度与体系总能量随模拟时间的趋势变化曲线。

2.3 升华焓

将单个分子周围留有足够空间可得到近似孤立分子模型，认为其与周期性边界条件周围分子无任何相互作用力。以ε-CL-20 为例，在NPT 系综和700 K、0 Pa 压力下反应20 ps，时间步长为0.1 fs。因分子尚未发生分解，取5～20 ps 平衡后能量均值除以分子数，作为凝聚态单分子能量。创建与上述晶胞大小相同的空盒，仅放入一个CL-20 分子，通过周期性边界条件预测孤立分子的能量，持续运算250 ps，取最后10 ps 轨迹的平均能量作为该分子的能量。该晶体分子晶格能（Elatt）由式（3）计算［27］：

式中，Es为单个固体分子能量，Eg为空盒子孤立分子所碎裂成原子的总能量，kJ。晶格能Elatt与升华焓成线性关系，根据Svatopluk 等［27］的含能材料晶格能和升华焓关系式Elatt=-1.2187ΔHsub+8.1804，对各晶型CL-20升华焓进行预测。

2.4 p-V 曲线拟合

为避免使用NPT 系综时，各方向独立控压可能导致的超晶胞在高压下的异常变形现象，参考低压实验［28］与高压DFT 模拟结果［29］的晶胞参数值，在NVT系综下改变盒子大小以控制压缩率，计算298 K 时模型所受的压力得到不同压缩比的p-V 曲线，使用连续介 质 中 的 三 阶Birch-Murnaghan 固 态 方 程［30-31］进 行拟合：

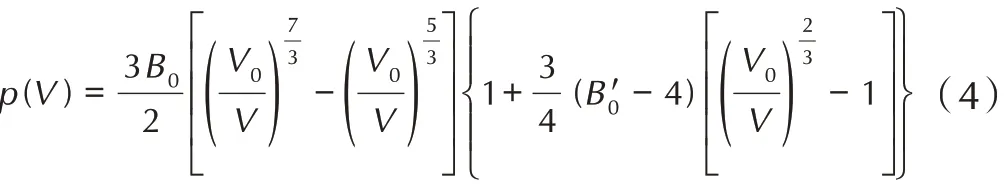
式中，p 为压力，GPa；B0与B′0分别为晶体的体积模量及其对压力偏导数；V0/V 为晶体初始体积与在该压力下的体积的比值。拟合三阶Birch-Murnaghan 固体状态方程，预测ε-、β-和γ-CL-20 的体积模量与其对压力偏导数，与已有报道对比。

2.5 均方位移与分子质心径向分布函数

编写程序计算ε-CL-20 分子的质心，计算相对初始原子位置的均方位移与分子质心的径向分布函数。因衍射实验值晶体模型与模拟优化值晶体模型的结构原子数量与顺序均相同，因此无需考虑质量加权。

不考虑质量加权的均方位移（RMSD）定义如下［32］：

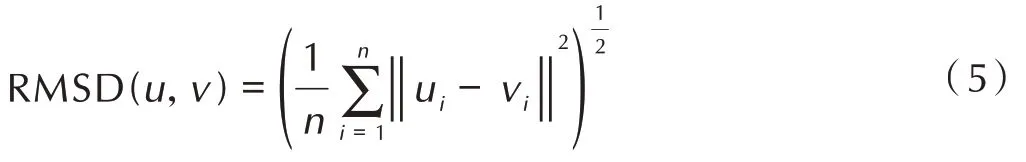
式中，u、v为两原子的位置坐标，i为原子序号。使用模拟值与初始值进行比对，RMSD 越小，代表两者结构越加相似，用该力场表示CL-20分子结构的置信度就越高。

同时，为验证密度突增现象是否对应晶胞内分子分布的变化，将相变温度对应密度突变前后状态的ε-CL-20 在NPT 系综下弛豫40 ps，计算晶胞内各个分子不同时刻的质心坐标，对距原点分子质心0～20 Å 范围内，的圆环内分子质心的出现概率进行统计（距离精度0.1 Å），归一化处理后绘制分子质心径向分布函数（RDF）曲线。

2.6 热膨胀及相变分析

充分弛豫得到平衡态ε-、β-和γ-CL-20 超晶胞，在0 GPa 和298～473 K 温度下进行40 ps NPT 模拟，时间步长0.1 fs，统计不同温度下晶胞参数与体积，分析各晶型CL-20 热膨胀系数与可能存在的相变现象。为探究γ 晶型在高压下的相变现象，在413 K、0～1 GPa下对γ-CL-20 进行计算。线膨胀系数和体积膨胀系数计算式如下：

式中，k 为线性系数；αn为膨胀系数（n=a、b、c、V），αn0分别为四个膨胀系数在常温下对应的初始值，K-1。

3 结果与讨论

3.1 力场适用性分析

3.1.1 常态下CL-20 晶胞参数

表1 给 出 了 在298 K、0 GPa 条 件 下，ε-、β-和γ-CL-20 的晶胞参数和密度，并给出与实验值相比［17］的RMSD 值。

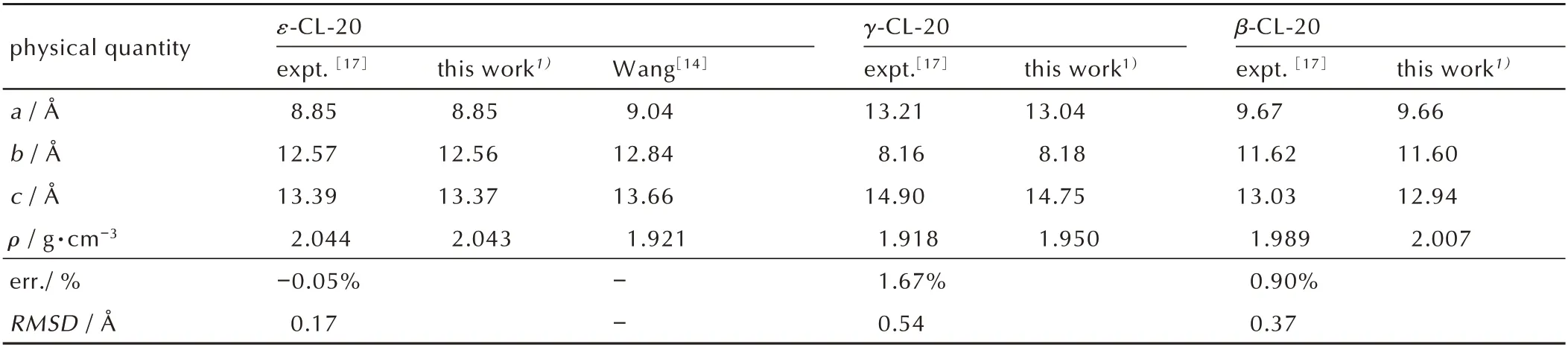
表1 各晶型CL-20 晶胞的平衡参数、密度与实验值对比Table 1 Comparison of equilibrium parameters，densities with experimental values of CL-20 cells

修正ReaxFF-lg 力场的价角势能截距，可减小非现实弱键对分子晶体体系能量的影响，提升该力场的准确度。从表1 可见，本文得到常温常压下ε-、β-和γ-CL-20 晶胞参数和密度与实验值误差低于2%，且三种晶型CL-20 与实验值的RMSD 值均在0.3 Å 左右，证明两者无几何偏差［32］，说明修正的ReaxFF-lg 力场对CL-20 的 适 用 性。Wang 等［14］采 用ReaxFF-lg 力 场 计算常温下ε-CL-20 密度（1.921g·cm-3）与实验值相差较大，可能是由于力场未经价角势能截距优化，导致体系进入亚稳定状态。

3.1.2 晶格能与升华焓

计算得到ε-、β-和γ-CL-20 的晶格能（EL）与升华焓（Esub），如表2 所示。由表2 可见，三种晶型CL-20 晶格能与Wei 等［26］报道的晶格能基本一致，误差在3%之内，优于Liu［33］的模拟结果。采用Svatopluk 关系式得到ε-、γ-和β-CL-20 的升华焓，其中ε-CL-20 的升华焓与Dorofeeva 等［34］在700 K 附 近 预 测 的 升 华 焓 相 符合。对比三种晶型CL-20 的晶格能可见，β-与γ-CL-20的晶格能大于ε-CL-20，说明ε 晶型稳定性高于其他两种晶型，与文献［26］报道一致。

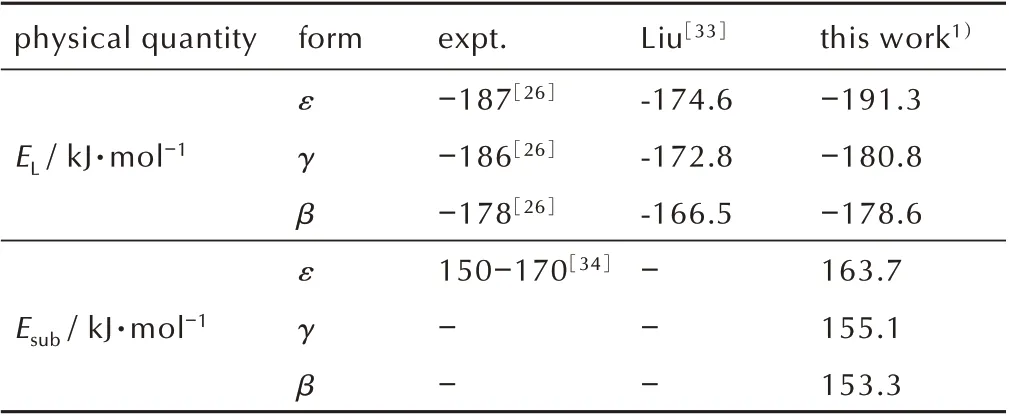
表2 三种晶型CL-20 晶格能与升华焓预测Table 2 Prediction of lattice energy and sublimation enthalpy of CL-20

3.1.3 ε-CL-20 的p-V 曲线

采用三阶Birch-Murnaghan 固态方程［30-31］拟合了0～280 GPa 压力范围内ε-CL-20 的p-V 曲线，如图1 所示。拟合得到体积模量（B0）及其对压力偏导数（B′0）见表3。

从表3 可见，在不同压力范围内，拟合所得ε-CL-20 的体积模量B0逐渐增大，反映了ε-CL-20 对外界均一性压缩的抗性增大；其对压力偏导数B′0趋近于4，说明随着压力增大，拟合结果趋近于二阶Birch-Murnaghan 固态方程。Gump 等［38］通过静水压测试，得到较低压力范围内ε-CL-20 的体积模量B0及其对压力偏导数B′0分别为（34.3±0.62）GPa 和（3.57±0.31）GPa，后续研究将数据校正为（13.6±2.0）GPa和（11.7±3.2）GPa［5］。Pu 等［35］和Sorescu 等［36-37］分别采用分子对接方法和色散力校正的密度泛函理论对ε-CL-20 的体积模量B0及其对压力偏导数B′0进行计算，计算结果均与Gump 等［5］的结果较接近，本研究在0～3 GPa 范围得到B0和B′0分别为（18.8±0.5）GPa 和（9.5±0.7）GPa，趋近于上述实验和模拟结果。Xu［29］等模拟了0～400 GPa 范围内ε-CL-20 的压缩特性，高压数据跟本研究拟合曲线较吻合，但对三阶Birch-Murnaghan 固态方程拟合度较差。

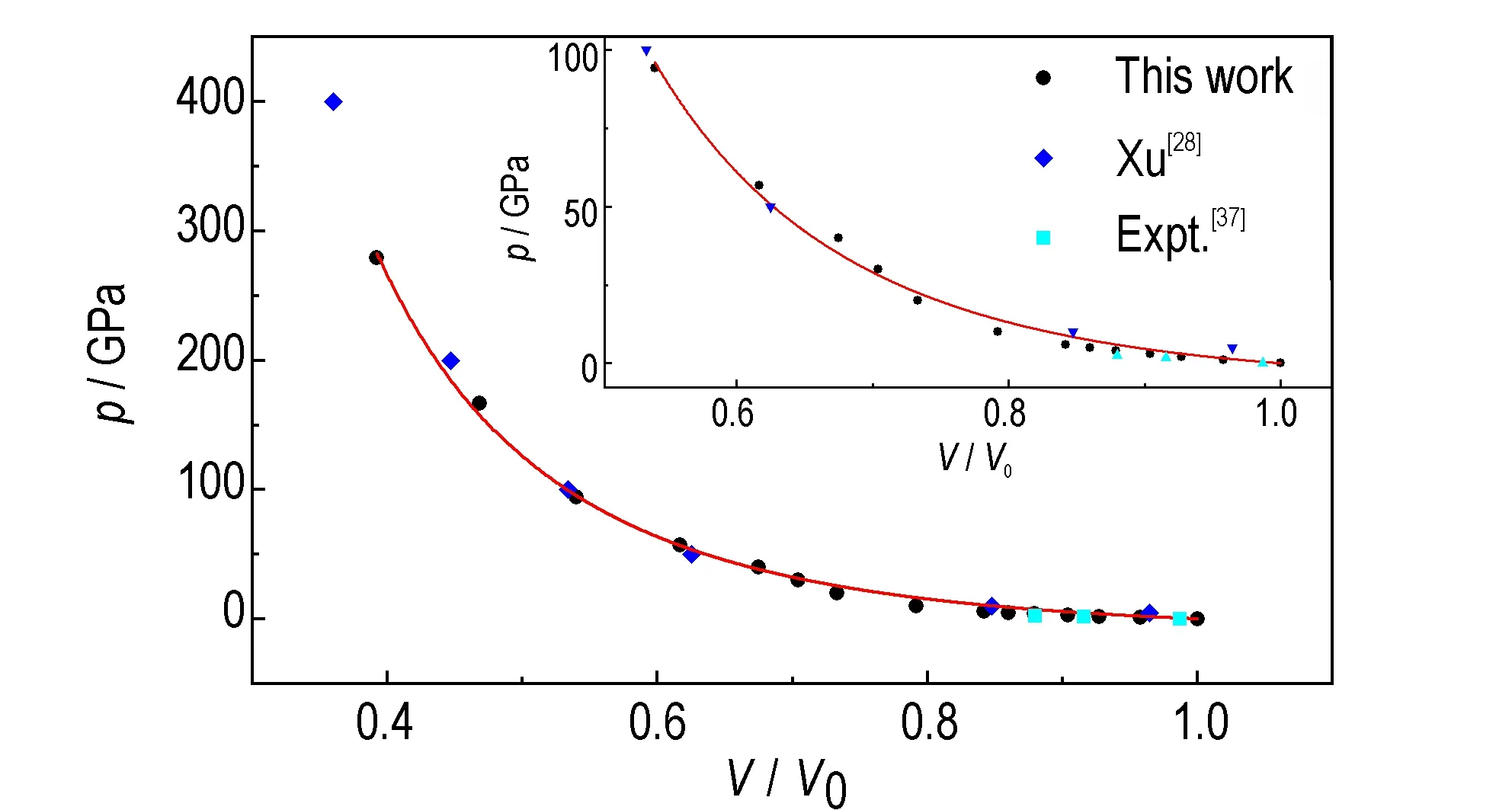
图1 ε-CL-20 的p-V 拟合曲线Fig.1 p-V curve of ε-CL-20

如上所述，研究依据晶胞参数、RMSD、晶格能、升华焓和p-V 状态函数等方面，说明了修正的ReaxFF-lg力场对各晶型CL-20 的适用性。上述结果说明本研究采用的修正ReaxFF-lg 反应力场能够可靠描述CL-20的压缩特性。

表3 ε-CL-20 的体积模量B0及其对压力偏导数B′0Table 3 Results of bulk modulus（B0）and partial derivative to pressure（B′0）of ε-CL-20

3.2 CL-20 高温相变分析

3.2.1 晶胞参数分析

考 察 了 在298～473 K 温 度 范 围 内ε-、β-和γ-CL-20 的密度变化，以及413 K 下γ-CL-20 密度随压力变化，如图2 所示。对423 K 温度下ε-CL-20 超晶胞中分子形貌变化进行了分析，如图3 所示。

在升温过程中，所考察三种晶型CL-20 晶胞参数与体积随温度上升均发生突变。从图2a 和图3 可见，ε-CL-20 在423 K 时发生晶胞参数突变，表现为密度快速下降，并略低于同温度γ 晶型。分子排布更为疏松，CL-20 分子中部分硝基的取向从赤道转向轴向，即转变为γ 晶型。如图2b 所示，将γ 晶型超晶胞在413 K下加压，在0.5 GPa 发生晶胞密度突增，超晶胞中部分CL-20 分子的一个硝基从轴向转向赤道，即转变为ε晶型，导致分子排布更加密集。Bircher 等［4］研究表明ε→γ 相变发生在347～437 K 升温过程中；Gump 等［5］提 出398 K 时 发 生ε→γ 相变，413 K 和0.4 GPa 条件下发生γ→ε相变。本文采用价角势能修正的ReaxFF-lg力场下得出423 K 时发生ε→γ 相变，413 K 和0.5 GPa下发生γ→ε相变，与上述两实验结果接近。

由图2a 可见，β 晶型在温度至448 K 时发生密度的突变，表现为分子的排布更加紧密，密度略有增大，推测发生β→ε 相变，导致密度增大。Russell 等［2］提出413～453 K 下发生β→ε 相变，与研究结果相符。

3.2.2 晶体结构变化

对398 K 与423 K 两个温度下ε-CL-20 超晶胞进行了RDF 分析，结果见图4。

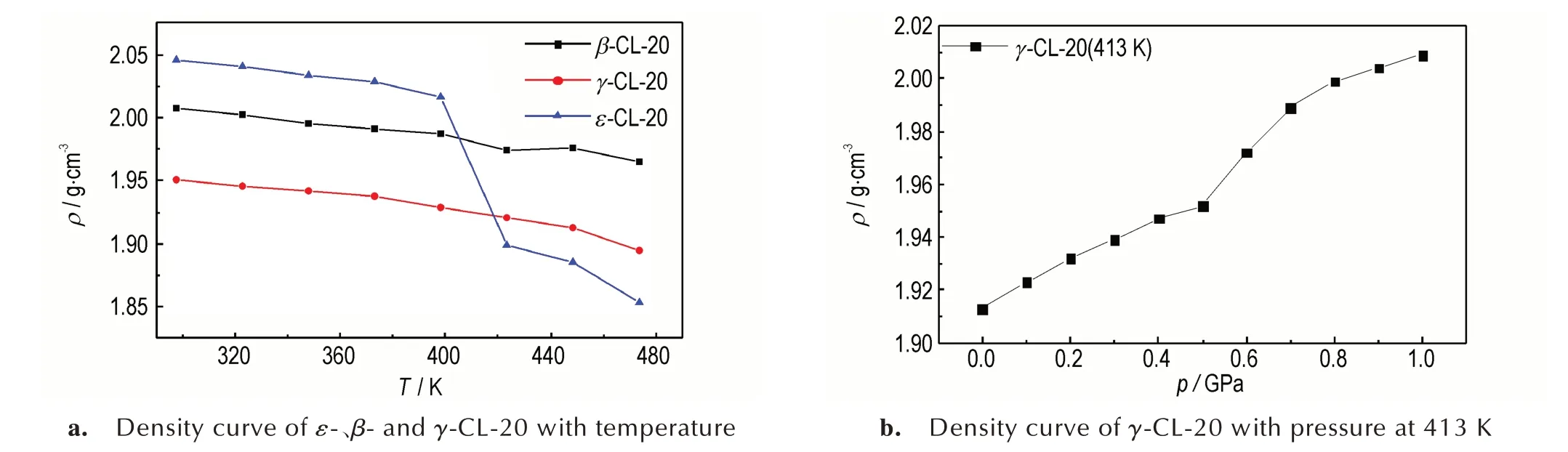
图2 各晶型CL-20 密度随温度或压力变化曲线Fig.2 Density curve of CL-20 with temperature or pressure

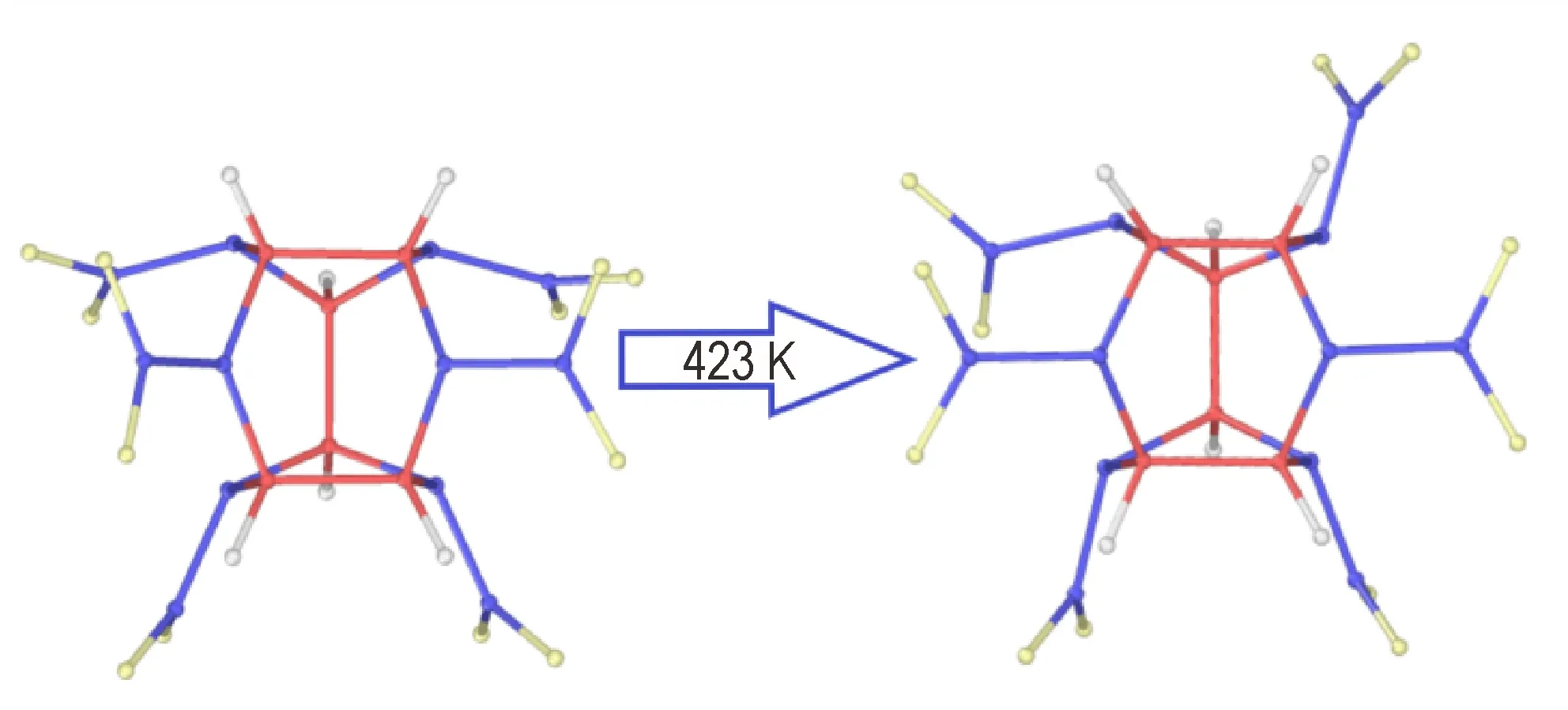
图3 423 K 时ε-CL-20 晶胞内分子形貌变化Fig.3 Change of molecular morphology in ε-CL-20 at 423 K

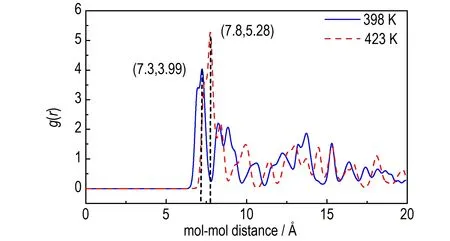
图4 398 K 与423 K 下ε-CL-20 晶体的RDF 分析Fig.4 RDF analysis of ε-CL-20 at 398 K and 423 K

观察升温过程中ε-CL-20 晶体内分子变化，发现423 K 时ε-CL-20 晶胞内部分分子中一个硝基从赤道位置转向轴向，证明发生ε→γ 相变（见图3）。RDF 曲线中第一波峰表示两个邻近分子质心的距离。根据Bolotina［15］的CL-20 晶体衍射数据在相应温度下进行RDF 分 析，结果表明ε 与γ 晶型CL-20 晶体内邻近分子质心距离分别为7.0 Å 与7.8 Å。从图4 可见，从398 K升 温到423 K 时，ε-CL-20 体 系 的RDF 第 一 波 峰位 置从7.3 Å 变为7.8 Å，超晶胞内分子质心分布发生明显变化，也证明升温过程中发生ε→γ 晶型转变。

3.2.3 热膨胀系数分析

对298～398 K 温 度 范 围 内ε-、β-和γ-CL-20 晶 胞参数和体积进行线性拟合，得到各晶型CL-20 线膨胀系数与体积膨胀系数，如表4 所示。

从表4 可见，ε-CL-20 三方向热膨胀系数差异小于2.5%，无明显各向异性，体膨胀系数较实验值大2.9%，计算结果与实验结果相符，证明力场对ε-CL-20分子作用力表达较为完备。Sorescu 等［39］采用RDX 势进行热膨胀模拟，结果a 方向的热膨胀系数明显小于b、c 方向，且体膨胀系数与实验值的误差超过50%。

β-CL-20 笼状结构上的氢原子在c 方向上与相邻分子所延展的硝基较为接近，将会在两者之间形成氢键，这些氢键的分布是交叉的，从而抑制了该方向的热膨胀，表现为c 方向的热膨胀系数远远小于其余两个方向［35］。表4 中β-CL-20 在c 方向的热膨胀系数略微小于a、b 方向，相比于实验值有所差异，这可能是由于力场对β-CL-20 分子间作用力的表达精度不足。而Sorescu 等［39］的模拟结果可见a 方向热膨胀系数明显大于b、c 方向，与实验值不符。

表4 ε-、β-和γ-CL-20 热膨胀系数Table 4 Coefficient of thermal expansion of ε-，β- and γ-CL-20

Pu 等［35］实验研究表明，γ-CL-20 在b 方向的分子堆积方式按分子质心连线可构成六元环单元，其中垂直于b 的H—O…N 分子间作用力在同类型键中较弱，导致热膨胀时六元环优先沿弱键方向膨胀，六元环沿b 方向畸变而产生负膨胀现象。本研究的结果表明，γ-CL-20 在b 方向热膨胀系数 显 著 小 于a 和b 方 向，数值相差达60%，表现出明显各向异性，与Pu 等的实验结果一致，但未表现出负膨胀的现象。而Sorescu等［39］计算结果中b 方向热膨胀系数反而有所增大，与实验值不符。

如上所述，本研究模拟得到ε-、β-和γ-CL-20 膨胀系数与Pu 等［35］的实验值较一致，显著优于Sorescu等［39］的热膨胀计算结果。由于ReaxFF-lg 力场对氢键作用的表述精度有待提高，导致了β-和γ-CL-20 的热膨胀各向异性差异不显著，有待对力场进一步改进。

4 结论

对ReaxFF-lg 力场进行价角势能截距修正，验证了该力场对含能材料CL-20 适用性，并在该力场下对CL-20 展开了热膨胀和相变研究，取得如下结论：

（1）计算了常温常压下ε-、β-和γ-CL-20 的晶胞参数、晶格能和升华焓，以及0～280 GPa 范围内ε-CL-20的p-V 曲线，表明修正的ReaxFF-lg 反应力场能够可靠描述CL-20 理化性质。

（2）高温相变研究表明，ε-CL-20 在423K 时发生ε →γ 相 变，β-CL-20 在448 K 时 转 变 为ε 晶 型，而γ-CL-20 在413 K 和0.5 GPa 转变为ε 晶型。

（3）热膨胀系数分析表明，ε-CL-20 在升温膨胀过程中无明显各向异性，与实验结果一致。而β 与γ 晶型CL-20 分别在c 方向和b 方向的热膨胀明显小于其他方向，表现出各向异性，与实验值有一定差异，需对ReaxFF-lg 的氢键作用进一步修正。