3～4 K温区热阻法温度波动抑制实验研究

潘小珊， 崔晓钰， 刘少帅， 杨志明， 蒋珍华， 吴亦农*

(1.上海理工大学 能源与动力工程学院， 上海 200093； 2.中国科学院 上海技术物理研究所， 上海 200083)

超导单光子探测器可实现远距离卫星测量，稳定可靠的3～4 K温区是探测器得以高性能工作的重要保障[1-4]。JT制冷系统具有体积小、重量轻、结构紧凑、机械振动小等优势，在空间长寿命任务中得到应用[5-8]。JT制冷机常用预冷冷源主要是脉管制冷机和斯特林制冷机等低温回热式气体制冷机，其换热部分为蓄热式换热器，冷热流体在其中周期性往复流过，导致制冷机冷头温度不可避免的随之产生温度波动，这对探测器工作是极其不利的。通常抑制冷头温度波动方法主要有被动控制法和主动控制法2种，被动控制法又分为热阻法和热容法。在热阻法抑制回热式制冷机冷头温度波动的研究上，国内外学者开展了很多工作。日本埼玉大学Yasuhiro Hasegawa等[9]在通过PID主动控制冷头温度的前提下，在GM制冷机二级冷头和铜块之间增加G10材料，在4.2 K时将冷头温度波幅从200 mK降低到5 mK。国内张祥等[10]在GM制冷机二级冷头和测温铜块之间添加不锈钢金属，在4.2～20 K时测温铜块温度波幅为3 mK。董斌等[11]在GM制冷机冷头和测温铜块之间增加聚四氟乙烯(PTFE)材料作为热阻尼器，使测温铜块温度波幅在20 K温度时小于4 mK。黄永华等[12]基于温度控制仪控制二级脉管制冷机冷头温度，在样品和冷头之间增加不同不锈钢叠片组合对温度波动进行抑制，在15 K时将冷头温度波幅抑制到5 mK以内。由于上述热阻法抑制冷头温度波动的研究都是在4～20 K的基础之上，更低温区的冷头温度对制冷机回热器周期工作更加敏感，冷头温度波动控制难度更大。目前国内外缺乏对4 K温区以下不同热阻对制冷机冷头和测温铜块之间传热热阻和温度波动之间的定量研究。课题组在黄永华团队的研究基础之上，采取10 μA激励电流高精度测温技术及多层防漏热措施，减少外界环境对温度波动的影响。基于GM制冷机进行实验研究和定量分析了3～4 K温区不锈钢厚度、叠片方式、传热热阻对温度波动、测温铜块和冷头的温差之间的关系，为更低温区热阻法抑制冷头温度波动的应用提供了参考。

1 热阻法抑制温度波动模型

热阻法抑制冷头温度波动模型如图1所示。

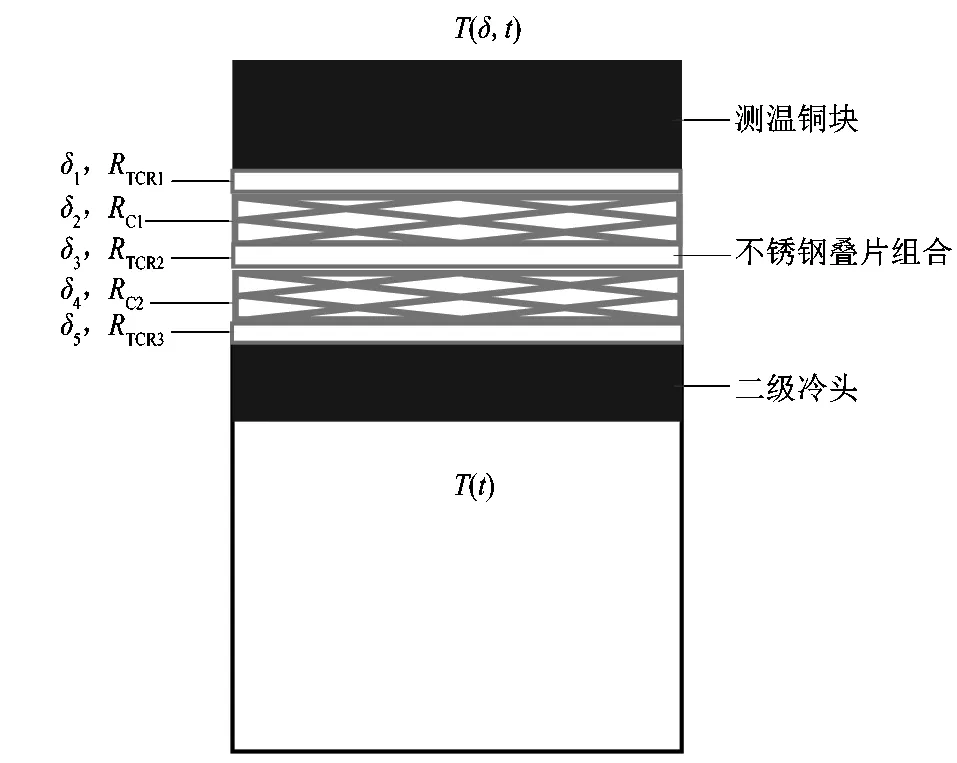
图1 热阻法抑制冷头温度波动模型Figure 1 Thermal resistance method to suppress cold headtemperature fluctuation model

如果不考虑添加抑制措施，制冷机冷头温度波幅一般不小于100 mK，基于工程实际应用，采用热阻法冷头温度波动抑制目标如表1所示。

表1 温度波动抑制目标

由于GM制冷机安装及所处的真空环境不同，其二级冷头温度波动状况不同。为了能更好地对制冷机温度波动进行控制，首先在原GM制冷机二级冷头上直接安装测温铜块进行温度波动测试。实验结果表明：由于热阻的存在，当二级冷头温度最终稳定在3.325 K时，温度波幅(波峰-波谷)约155 mK，波动频率约为1 Hz，其温度波动曲线图如图2所示。

GM二级冷头温度以类正弦曲线形式震荡，假设制冷机冷头和测温铜块之间未加入不锈钢片时制冷机冷头温度波幅(波峰-波谷)为A0，加入不锈钢后测温铜块温度波幅为A1。则二级冷头温度可以表示为：

(1)

式中：f为特征频率，Hz；t为特征时间，s；Tm为冷头平均温度，K。假设加入不锈钢片后，测温铜块温度仍以正弦曲线形式震荡且震荡频率不变，假设震荡幅值为A(δ)，初相为φ(δ)，对测温铜块温度建立数学模型：

T′(δ，t)=A(δ)sin (2πft+φ(δ))+Tm1。

(2)

式中：Tm1为测温铜块平均温度，K；δ为冷头与测温铜块之间不锈钢叠片的厚度，m；φ(δ)为sin函数关于δ的初相。加入不锈钢片后，由于整个实验台处于高真空状态，并在外围设置了防辐射冷屏和绝热多层材料，所以可以忽略对流换热和辐射换热，其传热可以看做一维非稳态导热过程。根据一维非稳态导热微分方程计算测温铜块温度[13]：

(3)

(4)

(5)

式中：a为热扩散系数，m2·s；ρ为固体材料的密度，kg/m3；c为材料比热容，J·(kg·K)-1；λ为有效导热系数，W·(m·K)-1。令A(δ)=eB(δ)并将式(2)分离变量可得：

T′(δ，t)=eB(δ)e(2πft+φ(δ))i+Tm1=e(B(δ)+φ(δ)i)e2πfti+Tm1。

(6)

式中：B(δ)为关于δ的一个变量。将式(6)代入式(3)中：

2πfi=a[B″(δ)+φ″(δ)i+(B′(δ))2+2B′(δ)·φ′(δ)i-(φ′(δ))2]；

(7)

2πfi=a[B″(δ)+(B′(δ))2-(φ′(δ))2]+a[φ″(δ)i+2B′(δ)φ′(δ)i]；

(8)

(9)

(10)

式中：c1，c2为常数。

通过求解可得测温铜块温度为：

(11)

故测温铜块温度波幅A1为：

(12)

2个表面接触，由于不可避免的表面粗糙度和表面起伏变形的存在会使其产生接触热阻，因此，本研究中温度波动模型中λ可以等效为：

(13)

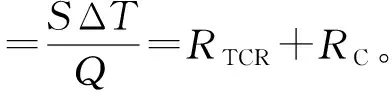
(14)

式中：RTCR为接触热阻，m2·K/W；RC为不锈钢导热热阻，m2·K/W；S为不锈钢间接触面积，m2；ΔT为测温铜块和冷头之间的温差，K；Q为通过不锈钢热阻的热量，W。当A0=0.155 K，f=1 Hz，ρ=7 980 kg/m3，c=5.920 3 J·(kg·K)-1时(4 K)，测温铜块温度波幅随不锈钢片厚度和有效导热系数变化曲线如图3所示。由图可知当GM制冷机二级冷头温度波动频率、热容和密度不变时，测温铜块温度波幅随着不锈钢厚度的增大和有效导热系数的减小而减小，而有效导热系数又是接触热阻和不锈钢导热热阻的函数，即可以通过增大二级冷头和测温铜块间的接触热阻和导热热阻的方法抑制冷头的温度波动。所以课题组通过在GM制冷机二级冷头和测温铜块之间增设不同叠片组合的不锈钢片，即增大测温铜块和冷头之间的导热热阻和接触热阻实现对温度波动的抑制。

图3 测温铜块上温度波幅随不锈钢片厚度和有效导热系数变化曲线Figure 3 Temperature fluctuation on copper blocks with stainless steel sheet thickness and effective thermal conductivity variation curve

2 实验系统

图4为本研究的热阻法抑制冷头温度波动实验装置。实验装置采用中船重工鹏力超低温技术有限公司生产的2级GM氦低温制冷机作为冷源。为了减少外界环境对温度波动测量值的影响，测试台安装在真空罐内并辅以真空泵组保持系统在10-7kPa的真空度。在二级冷头上布置一、二级防辐射冷屏，并在一级冷屏外包裹绝热多层材料。为了减小测温导线热阻对测温精度的影响，实验装置温度传感器采用四线制接法，并采用低导热系数磷青铜材料作为导线。由于本研究的总传热热阻是通过热量和温差计算的，为了减少温度传感器自热效应对温差测量的影响，实验台采用10 μA恒流源对温度传感器进行激励，并采用LabVIEW程序对温度数据进行实时采集。

不同厚度和不同数量的不锈钢叠片组合如表2所示。由于课题组主要是对热阻法抑制冷头温度波动进行研究，所以为了减少热容对实验的影响，所有的不锈钢片截面积、材料型号都一致。为了使每片不锈钢片接触热阻数值相同，所有不锈钢片表面粗糙度都相同，且都通过扭矩扳手施加相同扭矩螺纹连接固定在GM制冷机二级冷头上。

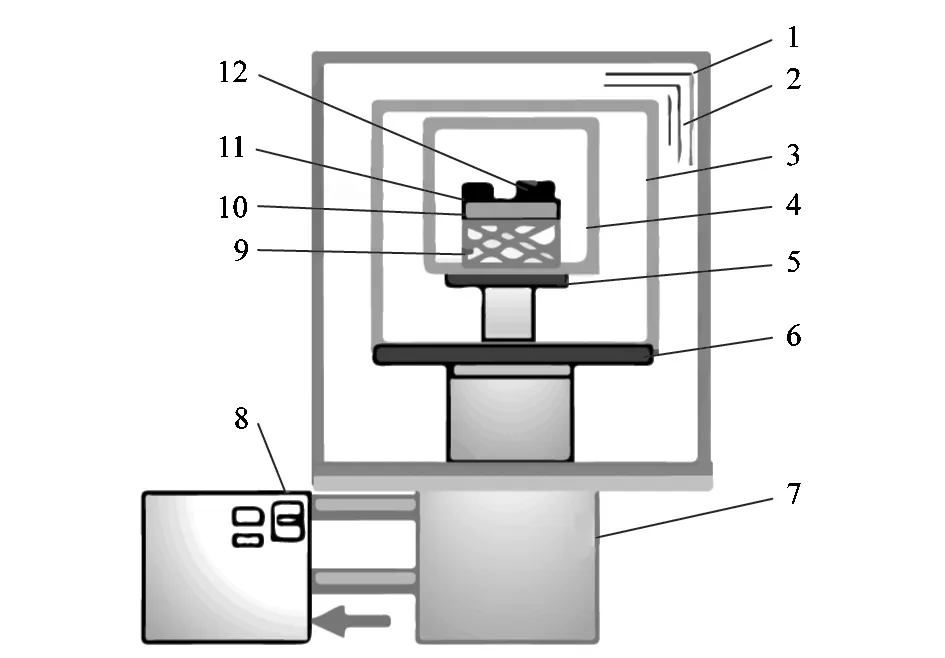
1—真空罐；2—绝热多层材料；3—一级冷屏；4—二级冷屏；5—二级冷头；6—一级冷头；7—GM制冷机；8—压缩机系统；9—不锈钢叠片；10—测温铜块；11—温度传感器；12—加热片。图4 实验装置图Figure 4 Experimental device

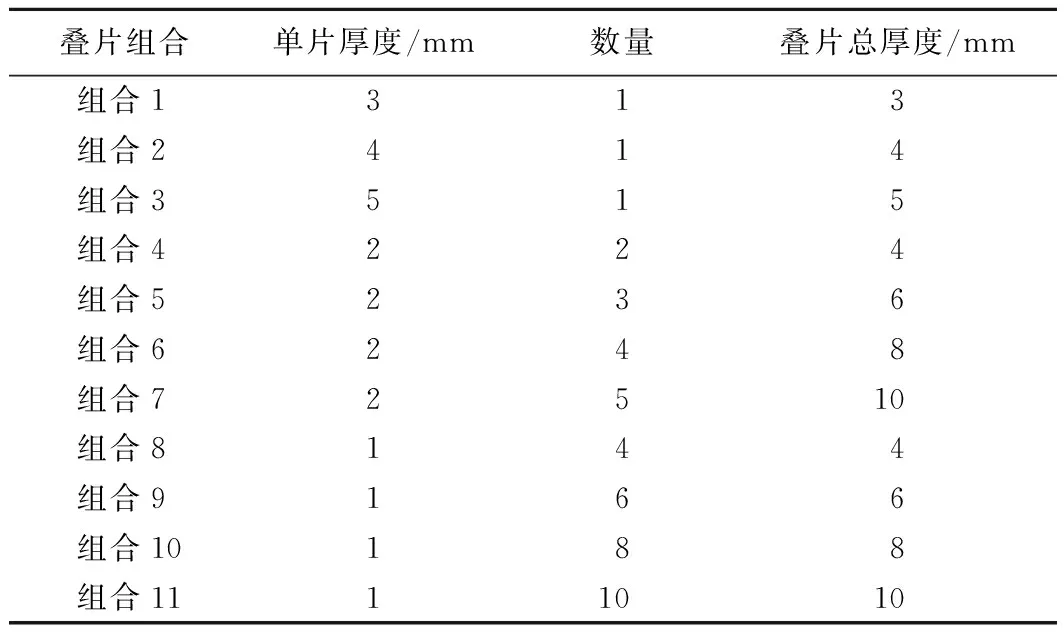
表2 不同厚度和数量的不锈钢叠片组合

3 实验结果及分析

基于上述实验装置，对11组不同组合不锈钢叠片对GM二级冷头温度波动抑制情况进行实验研究。图5～8分别为GM二级冷头温度为3.3 K附近时不同组合不锈钢叠片的实验结果。由图5可知，不改变冷头和测温铜块之间的总接触热阻时，随着单片不锈钢厚度的增加，冷头和测温铜块之间的导热热阻增大，测温铜块和冷头之间的总传热热阻也随之增加，测温铜块温度波幅减小，但是测温铜块和冷头上的温差也随之增大。当δ=3 mm时，温度波幅A1(波峰-波谷)约为65 mK，温差为20 mK；当δ=4 mm时，温度波幅A2约为40 mK，温差为40 mK；当δ=5 mm时，温度波幅A3约为27 mK，温差为63 mK。

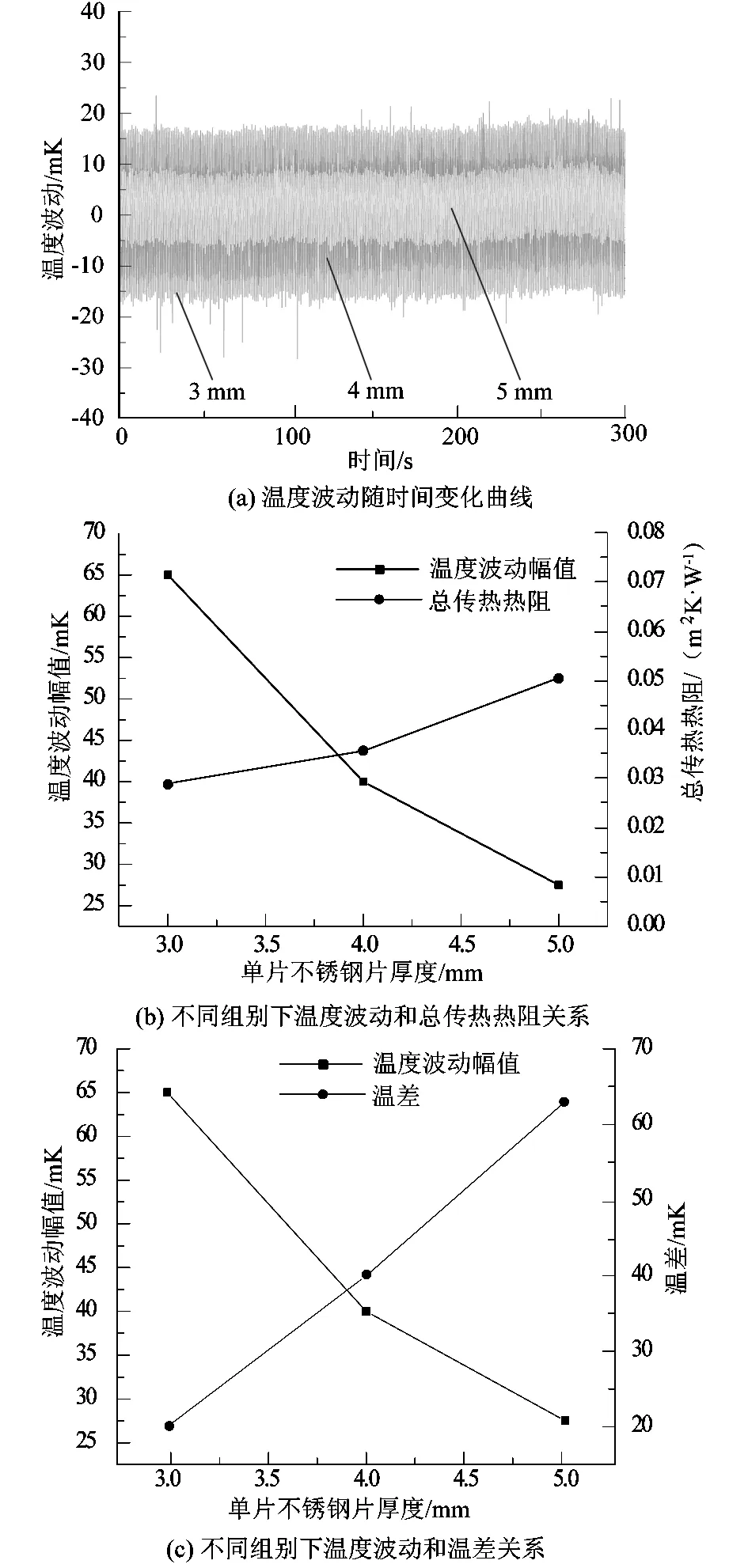
图5 组合1～3测温铜块上温度波幅Figure 5 Temperature fluctuations on copper blocksof group 1～3

不锈钢叠片组合1片(δ=4 mm)，2片(δ=2 mm)，4片(δ=1 mm)对冷头温度波幅抑制情况如图6所示，当不锈钢总厚度相同时，随着不锈钢叠片数的增加，测温铜块上的温度波动减小。这是由于叠片数的增加使得测温铜块和冷头之间的接触热阻增多，测温铜块和冷头之间的总传热热阻也随之增加，测温铜块温度波动减小。当组合为4片(δ=1 mm)，温度波幅A8(波峰-波谷)约为35 mK，温差为51 mK。由此可知，不改变不锈钢导热热阻(厚度)只增加接触热阻(叠片数)时，由于总传热热阻的增加，测温铜块温度波幅也随之减小。由以上可知，增加导热热阻或接触热阻都能起到抑制冷头温度波动的效果。

图6 组合2，4，8测温铜块温度波幅情况Figure 6 Temperature fluctuations on copper blocks of group 2，4 and 8

为了进一步研究冷头和测温铜块之间的总传热热阻对抑制温度波幅的效果，对不同厚度的不锈钢叠片组合(组合4～11)进行实验研究。由图7可知，当单片不锈钢厚度为2 mm，随着不锈钢片数的增加，冷头和测温铜块之间的总传热热阻增大，测温铜块温度波幅减小，温差增大。当δ=4 mm时，温度波幅A4(波峰-波谷)约为37.5 mK，温差为43 mK；当δ=6 mm时，温度波幅A5约为27.5 mK，温差为53 mK；当δ=8 mm时，温度波幅A6约为12.5 mK，温差为80 mK。当δ=10 mm时，温度波幅A7约为11 mK，温差为92 mK。

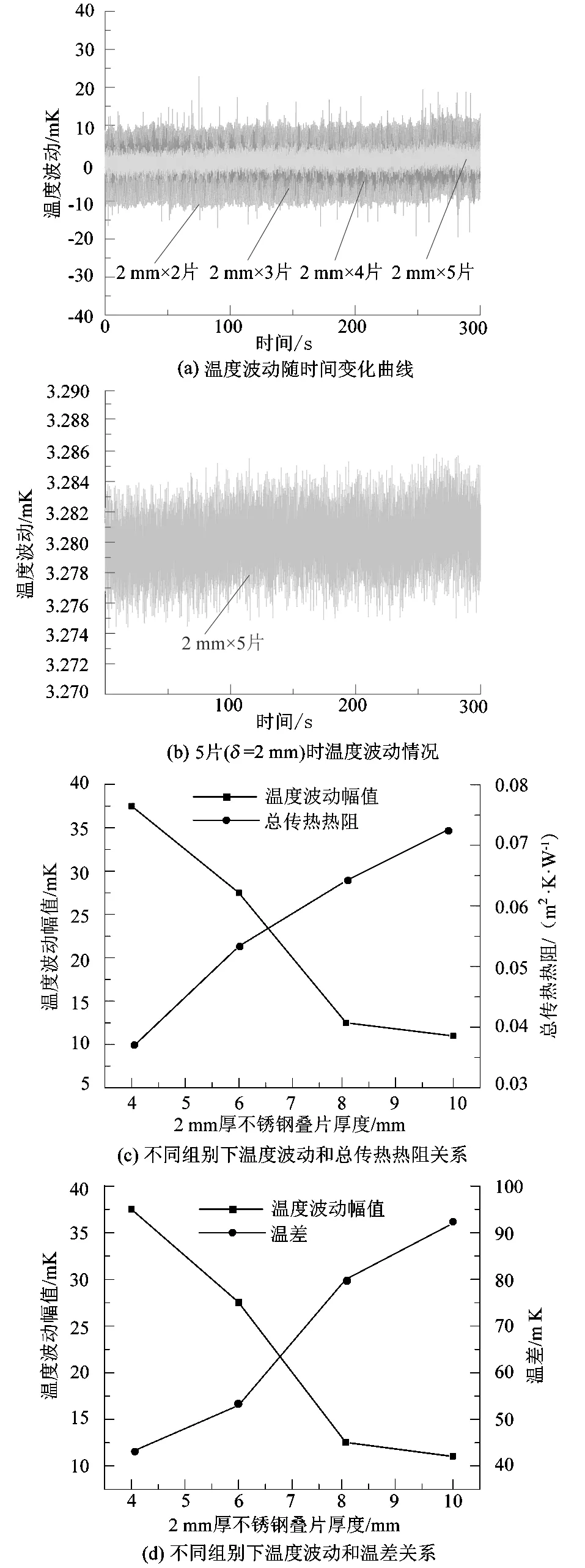
图7 组合4～7测温铜块上温度波幅Figure 7 Temperature fluctuations on copper blocks of group 4～7

由图8可知，当单片不锈钢厚度为1mm，随着不锈钢片数的增加，冷头和测温铜块之间的总传热热阻增大，测温铜块温度波幅减小，温差增大。当δ=4 mm时，温度波幅A8(波峰-波谷)约为35 mK，温差为51 mK；当δ=6 mm时，温度波幅A9约为20 mK，温差为82 mK；当δ=8 mm时，温度波幅A10约为10 mK，温差为90 mK。当δ=10 mm时，温度波幅A11(波峰-波谷)约为8 mK，温差为102 mK。

综上所述，不锈钢叠片组合总传热热阻对GM制冷机冷头温度波动抑制效果明显，通过增加不锈钢厚度即增加不锈钢热阻和增加不锈钢叠片之间的接触热阻都可以达到减小冷头温度波动的效果。相同总厚度下，单片1 mm厚度的不锈钢片组合对温度波动的抑制较厚度为2 mm的不锈钢片组合效果更好。10片厚度为1 mm不锈钢片组合对冷头温度波动抑制效果最好，冷头温度3.3 K时，温度波幅由155 mK降低至8 mK，此时测温铜块和冷头温差为102 mK。

4 结论

课题组研究了在3～4 K温区，测温铜块和制冷机冷头之间的总传热热阻对冷头温度波动抑制情况。通过改变测温铜块和冷头之间不锈钢叠片的厚度和数量对冷头温度波动抑制效果进行实验研究和定量分析，得到了总传热热阻、温差和温度波幅之间的关系。

1) 对热阻法抑制冷头温度波动模型进行理论分析可知，当GM制冷机二级冷头温度波动频率、热容和密度不变时，测温铜块温度波幅(波峰-波谷)随着不锈钢厚度的增大和有效导热系数的减小而减小，而有效导热系数又是接触热阻和不锈钢导热热阻的函数，即可以通过增大二级冷头和测温铜块间的接触热阻和导热热阻的方法抑制冷头的温度波动。

2) 不改变冷头和测温铜块之间的总接触热阻时，随着单片不锈钢厚度的增加，冷头和测温铜块之间的导热热阻增大，测温铜块和冷头之间的总传热热阻也随之增加，测温铜块温度波幅减小，但是测温铜块和冷头上的温差也随之增大。

3) 不改变不锈钢导热热阻(厚度)只增加接触热阻(叠片数)时，测温铜块温度波幅也随之减小。这是由于叠片数的增加使得接触热阻增多，测温铜块和冷头之间的总传热热阻也随之增加，测温铜块温度波幅随之减小。

4) 相同总厚度下，单片1 mm厚度的不锈钢片组合对温度波动的抑制较厚度为2 mm的不锈钢片组合效果更好。10片厚度为1 mm不锈钢片组合对冷头温度波动抑制效果最好，在3.31 K温度将155 mK的冷头温度波幅抑制到8 mK，此时测温铜块和冷头温差为102 mK。

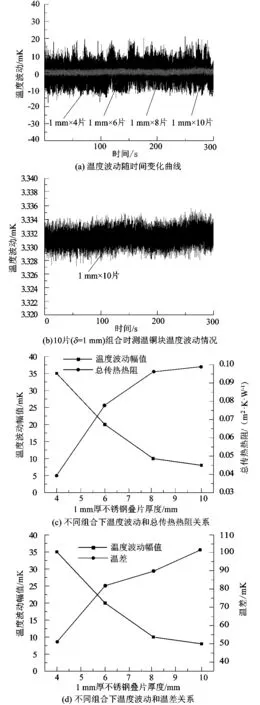
图8 组合8～11测温铜块上温度波动情况Figure 8 Temperature fluctuations on copper blocks of group 8～11