学生视角:让数学学习接地气
王淑芳
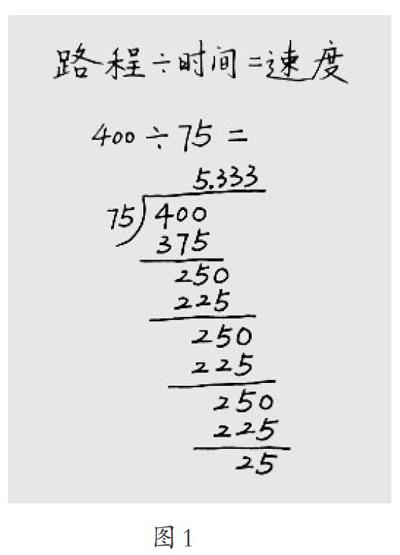

学生视角,即教师俯下身子从学生的认知视角出发,顺着学生的认知思路展开教学,让学生较好地理解数学知识的本质,促进其学习力和数学核心素养的提升。学生视角不仅是一种教学观念,更是一种教学方式。学生视角不是一蹴而就的,需要一系列复杂的思考和实践过程才能找到门道。笔者以人教版小学数学教材五年级上册“循环小数”教学为例,阐述学生视角的内涵及践行所需要的阶段和相应环节。
一、解读教材,厘清本质
践行学生视角的前提是教师要深刻理解教学内容,认真解读教材,厘清知识本质。在教学“循环小数”时,教师利用教材中的例7,首先以运动会场景图为素材,让学生迅速明白要求的是王鹏跑步的速度,马上想到“路程÷时间=速度”,从而快速列出算式。接着以“400÷75”的竖式计算为样本,让学生发现计算过程的规律。教材呈现了三个规律:永远除不完、商的小数部分重复出现3、余数25依次不断重复出现。这三个规律哪一个最关键呢?笔者认为,余数25依次不断重复出现,导致算式除不尽,也导致商的小数部分重复出现3,因此“余数25依次不断重复出现”这一规律最关键,要特别关注。
教材中的例8安排了两道算式,让学生先计算,再说一说商的特点。笔者认为,第一道算式和例7类似,都是商的小数部分重复出现一个数字,可以省略。第二道算式的商重复出现两个数字,是新的循环形式,应该重点关注。在学生有所体验的基础上,教师再揭示循环小数、循环节的概念以及循环小数书写的简便形式。
教师最后引导学生观察“15÷16”和“1.5÷7”这两道算式的商,让学生直观地认识什么是有限小数,什么是无限小数。循环小数当然是无限小数,但无限小数不一定是循环小数,教师可借助相应例子让学生领会这种关系。
二、课前调查,把握学情
解读教材可以厘清知识起点,但知识起点不一定是学生的实际起点。因此,要想让学生视角落在实处,课前还是要通过一定的方式了解学生的实际起点。教师在班上做了一个小调查,调查问题如下。
1.大家听说过循环小数吗?(5个学生举手)
2.你们认为循环小数是怎么样的?(第一个学生:循环小数就是除不完的小数。第二个学生:循环小数就是有数字循环出现的小数。第三个学生:0.33333…就是循环小数。第四个学生:循环小数就是有一个数字循环出现的小数。第五个学生:我只是听说,没看到过。)
经过调查,笔者了解到全班近一半学生听说过循环小数,也可能知道循环小数的一些特点,但这些“知道”都是碎片化的、不完整的。由此可见,教师不能完全照搬参考用书及参考资料上的做法,一定要在课前了解学生的真实起点,选择适合本班学情的教学方法。
三、顺应学生,层次推进
教师在教学时要努力顺应学生,然后有层次、有节奏地推进,这是践行学生视角的关键。笔者在解读教材及学情调查的基础上,决定以教材上的思路为主,适当做了一些调整,经历了如下的教学过程。
(一)算用结合,列式计算
算用结合有助于将计算与问题解决融为一体,适合学生视角,是新教材编排的一大特色。笔者先出示教材中的例7主题图,然后依次围绕下面三个问题展开教学。
1.“平均每秒跑多少米”是求什么?
2.怎么求速度?
3.真的除不完吗?
这一教学环节显得干脆利落,在算用结合中把学生迅速引向列式计算,让学生初步感受循环小数的特点。当学生纷纷表示除不完的时候,笔者顺势和学生一起在黑板上计算,展示计算过程(如图1)。
(二)观察算式,发现规律
呈现计算过程有利于学生发现规律。根据黑板上的算式,笔者依次围绕下面四个问题展开教学。
1.观察这个竖式,你发现了什么?
2.商的小数部分重复出现“3”的原因是什么?
3.算式除不完的原因是什么?
4.这三个规律,最关键的规律是哪一个?
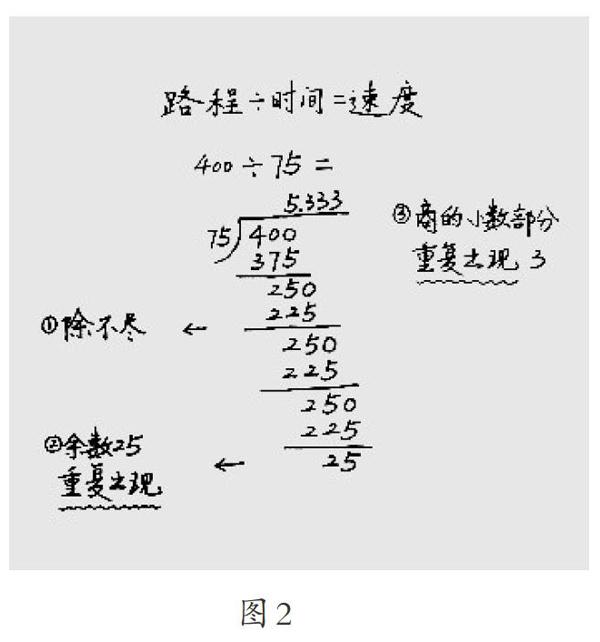
学生在回答第一个问题时,笔者根据学生回答情况适时在算式旁边板书三个规律:永远也除不完、余数25重复出现、商的小数部分重复出现3(如图2)。
在抛出第二个问题后,学生不知不觉地把目光聚向余数,当余数25第一次出现时,商出现3;第二次出现时,商出现3;第三次出现时,商又出现3。于是学生纷纷明白:原来余数出现25,商的小数部分就出现3,因此商的小数部分重复出现3的原因是余数25重复出现。有了解决第二个问题的经验,第三个问题就可以迎刃而解。
当解决了前三个问题后,第四个问题也就水到渠成,最关键的规律就是余数25重复出现。至此,学生自然就建立起这样一个观念:余数重复出现会造成商的小数部分重复出现某个数字;余数重复出现,除法竖式就除不完。
(三)认识名称,体验变化
学生的感性认识是建立数学概念的必要条件。在学习例7的基础上,笔者顺势提出“5.3333…”就是循环小数,重复出现的3只要写一个3,但要在它的上面点上一点,这个点就叫作循環点,表示重复出现。这个循环小数读作:五点三,三循环。然后写好单位,把题目做完整(如图3)。
然后,笔者引导学生围绕下面几个问题展开教学。
1.结果是循环小数吗?它的简便形式怎么表示?
2.为什么商的小数部分会有两个数字重复出现?
由于商的小数部分中的45重复出现,学生都知道这是循环小数。简便形式就是商的小数部分重复出现的45只写一个,并且在4和5上面点上循环点。
由于有了上一环节的知识,学生会知道因为余数5和6依次不断交替重复出现,所以商的小数部分就会重复出现45。这样一来,学生加深了对循环小数的认识。
(四)提炼特征,建构概念
在学生感性经验积累到一定程度的时候,适度的提炼有利于学生更好地厘清概念本质。笔者在完成上一教学环节的基础上,让学生阅读教材33~34页的内容,然后围绕下面三个问题展开教学。
1.這两个循环小数共同的特征是什么?
2.什么叫依次不断?什么叫循环节?
3.什么叫循环点?如何点?
在回答第一个问题后,笔者顺势板书:小数部分的一个数字或几个数字依次不断重复出现。
第二个问题,学生会根据板书回答:“依次不断,就是按顺序重复出现,不会停下。”学生也会明白小数部分重复出现的数字叫循环节,抓住教材中的“6.9258258…”这个循环小数,让学生明白它的循环节是258,它是重复出现的,后面的省略号就表示依次不断重复出现。
第三个问题,同样抓住“6.9258258…”这个循环小数,它的循环节有三个数字,在此强调循环节有三个或三个以上的,只要在首和尾两个数字上点循环点就可以,中间的数不用点循环点。
(五)定向训练,巩固新知
有针对性的定向训练是巩固新知的必要手段。本节课涉及知识点较多,考虑实际学情,笔者不想过多拓展,只围绕核心知识点设计练习,有助于学生厘清知识要点。
1.判断。
(1)一道除法算式,发现余数总是34,那么商肯定是一个循环小数。()
(2)9.99999÷3的商是一个循环小数。()
(3)两个数相除,除不尽时,商是无限小数,而且是循环小数。()
2.比大小。
0.123○0.12 0.9999999○0.9
2.268○2.267 0.1234○0.123
3.用简便形式表示循环小数。
1.5555… 1.7676… 1.2567567…
4.下面这个数的小数部分第99位是什么数字?小数部分前99位数字的和是多少?
0.234234…
第1题重在巩固循环小数的本质特征、相关概念与无限小数的关系;第2题重在巩固循环小数的特征;第3题重在巩固循环小数的简便记法;第4题重在巩固学生对无限小数概念的理解,拓展学生的抽象思维。
总之,学生视角可以让数学学习更接地气。有了学生视角,我们就会考虑学生的学习起点、学习重点和难点、容易混淆的知识点、练习设计的针对性……由此可见,学生视角是促进学生学习力和数学核心素养提升的有效手段。
(作者单位:浙江省仙居县田市镇中心小学)

