基于CCD法的应变式测力仪优化设计*

郭 强，赵知辛，薛旭东，潘晓阳

(陕西理工大学机械工程学院，陕西 汉中 723000)

0 引言

在切削过程中，切削力对刀具寿命、切削加工的温度及成形后表面质量有重要的影响[1-3]。在许多机床上，切削过程中加入了切削力的实时监测，以实现对一些成本较高、加工要求苛刻零部件的精确加工。针对现有测力仪结构出现的一些问题[4]，譬如：抗干扰能力差、易受外界影响、在较大应变测量时结果出现较大的非线性等。如何提高切削力测量的精准度和灵敏度，成为当前测力仪理论及应用研究的方向之一。

针对上述问题，国内外诸多学者展开了相关研究。如Korkut I[5]基于应变测力计开发了相关数据采集系统，在一定载荷范围内可以保证较低的交叉灵敏度；易力力等[6]研发了新型切削力测量装置，通过对三向电的校准，确保相关响应系数稳定；Panzera T H等[7]通过方差分析，验证了设计的应变测力计在切削深度上具有和压电式测力计具有相近性能； Sheikh-Ahmad J Y等[8]通过有限元法确定应变节点和灵敏度节点位置，并研制了一种搅拌摩擦焊测力仪，通过试验发现具有高线性响应，受干扰较小；刘明尧等[9]将光栅应变传感器用于检测切削力，通过试验发现能有效的避免电磁影响。

大多学者通过开发相关系统或研究传感器来提高测量精度，根据相关文献[10-12]可知，使用灵敏度较高的应变传感器可以提高传递率、提高传感器弹性体固有频率可以改善响应特性。本文将通过对测力仪本身结构进行优化，提高测力仪的应变与结构一阶固有频率来提高应变片感知变形的能力，在降低测量误差的同时降低切削过程中产生结构共振的可能。

1 测力仪结构参数及工作原理

测力仪结构组成如下：刀具、刀具装夹体、弹性体(粘贴应变片)与底座，结构简图如图1a所示。刀具装夹在刀架上，通过弹性体与底座相连，应变片则贴在弹性体上，如图1b所示(标明数字处为粘贴应变片位置)。本文采用的材料为沉淀硬化钢(17-4PH)，这种材料具有高强度、高硬度与较好的耐腐蚀性等，被广泛运用于民用工业。测力仪主要材料属性如表1所示。

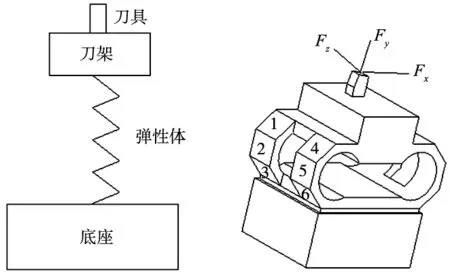
(a) 结构简图 (b) 三维示意图图1 八角环测力仪

表1 八角环材料属性

八角环测力仪原理由圆环演变而来[13]。圆环的受力分析如图2所示。Fx使4个圆环受到切向力；Fy使4个圆环受到压力；Fz使4个圆环上半部受拉，下半部受压。受到载荷作用圆环表面将产生变形，使粘贴在圆环外壁的应变片感知，应变片产生变形。根据应变片形成的电桥电路，通过应变量与载荷关系可以求出作用力[14]。

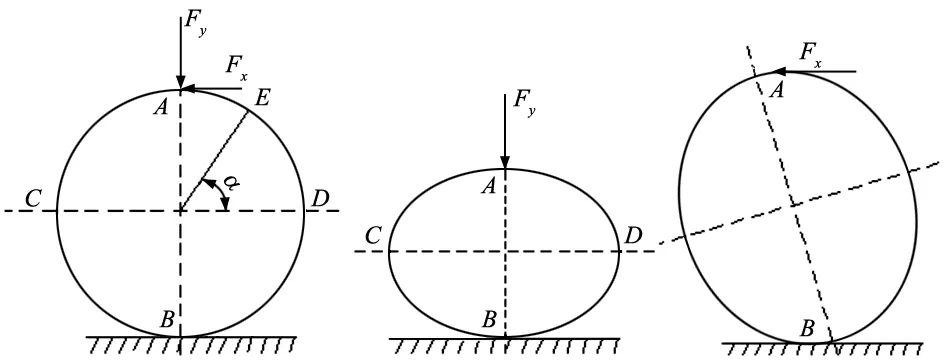
(a)未变形 (b)Fy作用变形 (c)Fx作用变形图2 圆环受力分析

由材料力学摩尔积分可得，当圆环受到径向力时，任一截面的弯矩[14]：

(1)

由上式可知：当α=0°(D点)时，弯矩与应变分别为：

(2)

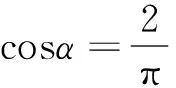
(3)

上式中，E为八角环弹性模量，b为八角环宽度，t为八角环厚度，r为八角环平均半径，相关参数如图3所示。

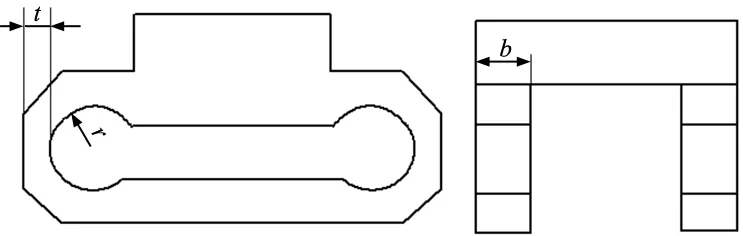
图3 部分结构参数示意图

假定Fx、Fy、Fz都是500 N，带入式(2)和式(3)中，计算出的应力值均在材料安全范围内。

2 有限元分析

2.1 静力学分析

通过有限元软件建立三维模型，把刀具装夹体及八角环进行网格细化，测力仪的约束条件为底座四周与底部约束，限制测力仪三方向自由度。通过施加载荷，分析出测力仪的应变与应力云图如图4所示。

(a) 应变云图

(b) 应力云图图4 测力仪应力云图

受到Fx作用时，测力仪沿Z向变形；受到Fy作用时，测力仪沿Y向变形；受到Fz作用时，测力仪绕Z轴旋转变形；同时受到Fx、Fy、Fz作用时，测力仪沿XY面倾斜变形。由分析可知测力仪的最大应力约3.9 MPa，最大应变约为1.9×10-5。测力仪产生的变形较小，且材料具有较高的屈服极限，结构满足强度要求。

2.2 模态分析

约束条件同静力分析相同，分析测力仪前6阶模态振型，其中第一阶振型云图如图5所示，前6阶振型描述如表2所示。

图5 一阶模态振型

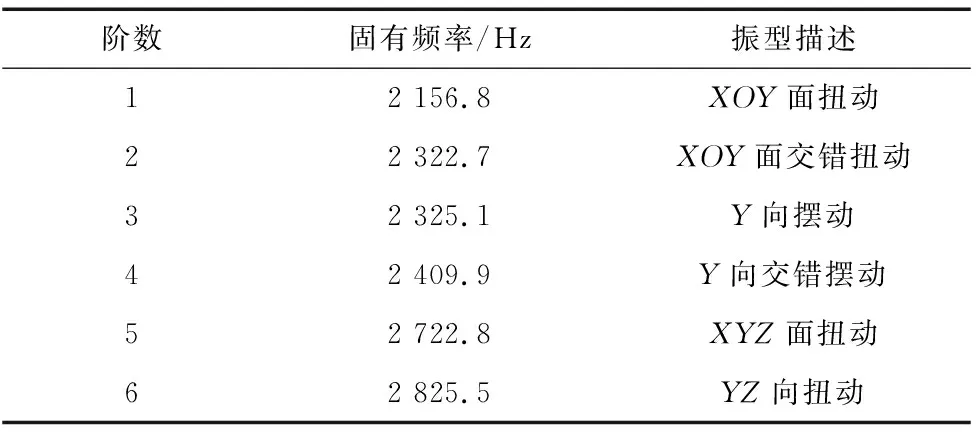
表2 八角环前6阶固有频率与振型

通过模态分析可知，多阶振型均集中在八角环的外壁处，即粘贴应变片位置。平稳的工作条件也是提高测量精度的一种措施，如果振动过大将影响测力仪正常工作，因此提高固有频率可以提高测力仪在工作状态下的抗干扰能力。

3 八角环结构优化

结构优化的目标是保证模型在约束条件下，尽可能使测力仪在同等载荷下的应变量和一阶固有频率得到提高。根据八角环的结构并结合有限元静力学分析结果，确定八角环的设计变量：内圆环半径P1、八角环外壁边长P2与同侧两圆环上下间距P3、P4。各参数与数值如图6与表3所示。

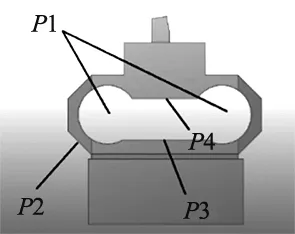
图6 设计参数

表3 设计参数初值(mm)

3.1 灵敏度分析

灵敏度分析是通过数学方法对输入参数与输出参数关系的分析，从而确定对结构影响较大的参数为优化参数[15]。测力仪的响应特征可通过灵敏度来进行分析比较。灵敏度分析数学表达式为：

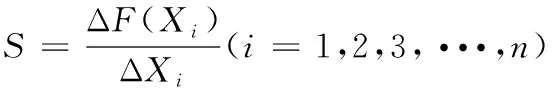
(4)

以上述4个变量作为设计变量进行灵敏度分析。通过迭代运算得到了4个设计变量对八角环的应变及固有频率的变化的关系，如图7、图8所示。

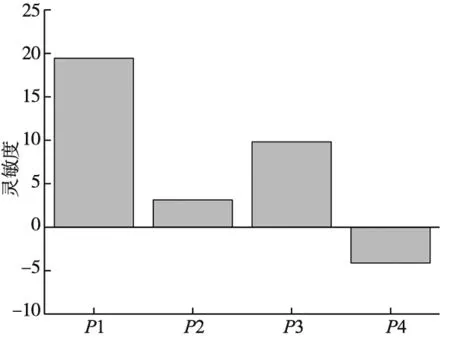
图7 应变灵敏度

图8 固有频率灵敏度

由图8与图9可知，测力仪环半径P1对应变和固有频率影响最大。结合式(2)和式(3)亦可知，在测力仪宽度和测力仪厚度不作优化参数时，测力仪环半径P1对应变的影响最大。变量P3和约束底座直接接触且接触面积较大，所以在受到切削力时测力仪发生振动的频率较低，因此P3对固有频率的影响非常小。但结合图8发现P3对应变的影响仅次于P1，综合考虑保留这4个变量作为优化参数。

结合有限元的仿真分析，确定变化范围，以提高应变量f1(P5)及一阶固有频率f2(P6)为目标，并约束一阶固有频率S。得出优化数学模型为：

3.2 响应面优化分析及结果

响应面法可以通过分析输入变量与输出变量的关系来简化优化程序。模型的建立一般是通过将有限元中产生的设计点作为样本数据，再构建模型进行处理，最终得到各参数的变化规律[16]。构建二阶响应面近似模型多项式为[17]：

(5)

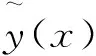
为了验证近似模型是否满足后期精度要求，可以采用决定系数R2进行判定。决定系数R2的表达式为：

(6)

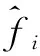
决定系数R2的数值越接近于1则表明拟合精度越高，越靠近工程实际工作情况[18]。

为了更好求解测力仪的应变及固有频率与各设计变量有关的二阶响应模型，采用CCD法对模型进行采样，得到多个样本试验点，取其中25个样本试验点进行最小二乘法计算并进行数据拟合，样本点数据如表4所示。

通过CCD法，分别对应变、固有频率进行拟合得到二阶响应面模型分别为：

F1max= -0.000076 + 10-7×(19.8828p1-15.4226p2-

0.18872p1p2-0.0004198p1p3-0.0158p1p4+

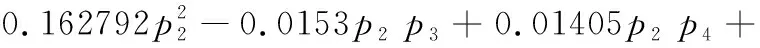
F2max= -14799.0362 + 125.9706p1+ 154.66582p2+

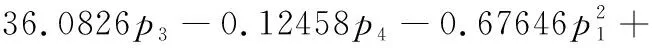
0.37107p1p2+ 0.08542p1p3-0.50875p1p4-

表4 设计样本点及结果

表5所示为上述两模型的决定系数。可以看出固有频率模型响应度大于应变，反应出应变的响应非线性程度较高。但决定系数数值都接近1，表明两个响应面模型精度满足要求，可以进行优化设计。

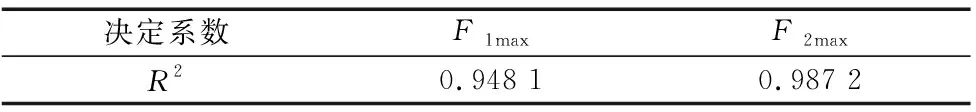
表5 各模型决定系数

4 优化结果分析

在静力学及模态分析基础上，以最大应变及提高一阶固有频率为目标，并在优化中对应变P6及固有频率P7进行相关设置，最终求解得到表6的三组候选点。

通过下表发现，候选点1与候选点2所求解的应变及一阶固有频率较为接近，且都低于候选点3的数值，结合优化目标选取候选点3作为最终优化方案。用候选点3作为优化法案可以发现：

变量P1、P2、P3相对于结构初值分别降低了约10%、7.5%和1.18%；而变量P4相对于结构初值提高了约5.75%。

应变值P5提高11.05%，较为明显，能使测力仪在同样的环境条件下更好感知应变片从而提高测量精度；一阶固有频率P6提高9.63%，增加了测力仪工作时抗干扰能力，使工作时更平稳，且优化后强度均满足要求。

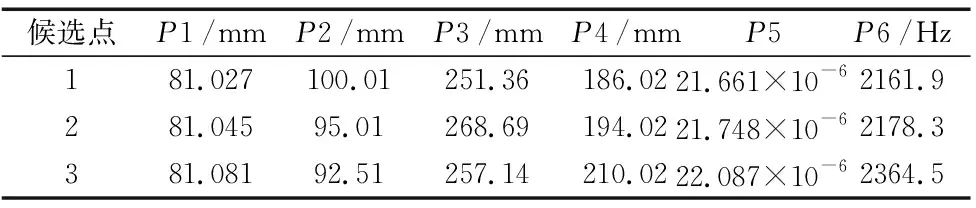
表6 优化参数候选点

5 结论

(1)采用响应面法对平行八角环测力仪进行结构优化，对CCD实验法产生的样本点进行了数据拟合，通过决定系数表明拟合良好，降低了优化工作量。

(2)优化后表明，基于响应面法的八角环测力仪优化设计，可以明显提高其应变量与固有频率，提高测力仪检测切削力的精度与工作时抗干扰的能力，为后续测力仪的研制与设计、提高测力仪的检测精度提供一种理论参考。同时制约应变式测力仪进一步发展的关键在于寻找线弹性范围更广的材料。