改进的蚁群算法在智能车辆路径规划中的运用*

蓝 丹，樊东红，陈 强，危 维

(1.广西生态工程职业技术学院汽车与信息工程学院，广西 柳州 545004；2.广西民族师范学院数理与电子信息工程学院，广西 崇左 532200；3.柳州电信分公司，广西 柳州 545004)

0 引言

随着互联网、大数据以及人工智能等高新技术在车辆领域的广泛运用，车辆正由人工操控加速向智能化系统控制转变，智能车辆已成为产业技术的战略制高点，受到广泛研究人员的关注[1-3]。路径规划作为智能车辆的核心技术之一，其主要功能是根据给定的环境模型，在一定约束条件下，规划出一条连接车辆当前位置和目标位置的无碰撞路径，是确保车辆正常行驶的关键，也是智能车辆技术研究中的重点[4-6]。

当前，大量学者对智能车辆路径规划问题开展了广泛的研究：文献[7]运用人工势场算法对车辆进行局部路径规划，实现了车辆在满足动力学约束以及平稳性、安全性要求前提下的避障换道，但仅限于规避静态障碍物；文献[8]在传统人工势场算法中引入速度斥力势场，以此规划出车辆运动的动态路径，实现了车辆的动态避障，且能满足车辆转向要求；文献[9-11]进一步对传统人工势场算法进行改进，引入调节因子，进行车辆运动的路径规划，较好的克服了陷入局部最优且不适用于动态环境等问题。以上是传统的人工势场法在车辆路径规划中的应用。随着人工智能技术的快速发展，模糊逻辑算法、遗传算法、快速扩展随机树等智能算法在车辆路径规划问题中也得到了较好的应用。文献[12]提出了一种分层分级的模糊控制方法，通过设计避障控制器和目标趋向控制器实现了车辆的运动避障，减少了算法的计算量；文献[13]对传统遗传算法进行改进，提出了一种车辆路径规划方法，大大提高了系统收敛速度；文献[14]设计期望避障路径模型，提出一种改进RRT路径规划算法，较好的解决了传统RRT算法随机性太大导致的路径不平滑问题，使得规划路径能够满足车辆动力学约束。

本文针对智能车辆路径规划问题，提出一种改进蚁群智能路径规划方法，较好地解决了传统蚁群算法搜索时间长和容易陷入局部最优等缺陷，在提高算法效率的同时保证了路径的平滑性并能实现实时动态避障，有效提高了车辆行驶的安全性。

1 传统蚁群算法原理及缺陷

在t时刻，蚂蚁k从栅格i转移到栅格j的概率为：

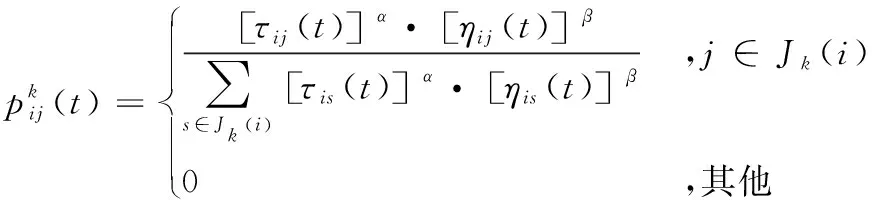
(1)

式中，Jk(i)表示蚂蚁k下一步可选栅格的集合。τij表示当前路径的信息素浓度，ηij表示一个启发因子，α和β分别表示信息素和期望启发因子的相对重要程度。

式(1)中，ηij具体表达式为：

(2)

式中，d(j,G)表示栅格j到目标栅格G的距离。

信息素更新公式为：

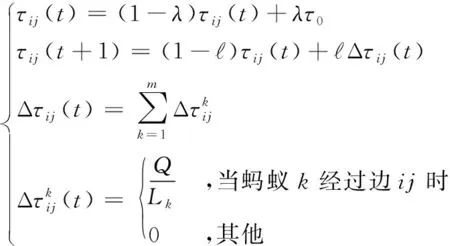
(3)

式中，λ为局部信息素挥发速率，表示全局信息素挥发速率，Δτij表示全局信息素浓度，Q为正常数，Lk为第k只蚂蚁在本次周游中的最短路径长度。

根据以上原理，算法的主要流程为：

步骤1：创建栅格化地图环境，输入由0和1组成的矩阵表示需要寻找最优路径的地图，其中0表示可行道路，1表示障碍物；

步骤2：信息素矩阵、初始点、终止点、启发因子等各类参数初始化设置；

步骤3：选择从初始栅格下一步的可行栅格，并根据路径的信息素浓度，通过公式(1)求得前往每个节点的概率，通过轮盘算法获得下一步的初始栅格；

步骤4：更新栅格路径以及路程；

步骤5：重复步骤3、4，直到蚂蚁到达目标栅格或者无路可走；

步骤6：重复步骤3、4、5，直到m只蚂蚁迭代结束；

步骤7：按公式(3)更新信息素矩阵，没有到达目标栅格的蚂蚁除外；

步骤8：重复步骤3～7，直到n代蚂蚁全部迭代结束。

从算法的基本原理和主要流程来看，传统蚁群算法主要存在以下缺陷[16]：

(1)由于蚂蚁寻找路径的随机性比较大，且初始时刻各路径的信息素大致相同，导致了搜索时间较长；

(2)根据路径选择概率公式，蚂蚁会朝着信息素浓度较大的路径前进，但当搜索规模较大时，容易陷入局部最优。

2 改进蚁群算法

2.1 优化路径选择概率

在传统蚁群算法中，从蚂蚁选择概率公式(1)可以看出，蚂蚁在选择下一步移动栅格时，取决于信息素浓度τij以及仅包含栅格j到目标栅格G的距离信息的启发信息ηij，完全没有考虑障碍栅格信息，算法通过提供的先验位置信息，判断可行区域，能够实现有效静态避障，但对于动态障碍物，此法失效。为保证蚂蚁能够有效实现动态避障，现将障碍栅格信息引入选择概率中。改进后的路径选择概率公式为：

(4)

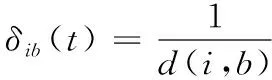
(5)

式中，d(i,b)表示障碍栅格与自由栅格的距离，γ为障碍距离的启发因子，用以表示δib(t)的重要程度。

同时为了增加路径选择的多样性，避免算法陷入局部最优，对启发式因子ηij进行改进：

(6)

式中，C为正常数。

2.2 改进信息素更新方式

在传统蚁群算法中的初期时，蚂蚁每进行一次移动时，走过路径的信息素都会按照一定的挥发速率而减弱，当搜索问题规模较大时，可能会导致该条路径信息素挥发至0，从而较低算法搜索能力，为此，对局部信息素挥发系数改进如下：

(7)

式中，0.95λ(t)表示取95%的信息素挥发因子的上限，λmin表示信息素挥发因子的下限。

同时，为避免某条路径信息素浓度过大或过小，而导致出现搜索停滞，对其做出范围限制如下：

(8)

通过改进局部信息素挥发系数以及限定信息素浓度的阈值，能有效防止某条路径上的信息素浓度过高或过低，从而实现在保证路径选择多样性的同时，提高算法的局部搜索能力和收敛性。

2.3 路径平滑处理

图1为智能车辆简化模型，考虑车辆处于较低速度行驶状态，此时车辆运行相对稳定，车辆转向灵敏性可通过转向半径来表示，具体表达式为[8]：

(9)

式中，R为车辆转向半径，δ为车辆前轮转向角，L为车辆轴距。

当车辆进入弯道转向时，应满足：

(10)

式中，车辆转向角通常在30°～40°，乘用车辆轴距一般在2.3～2.45 m之间，取δmax=40°，取Lmax=2.45 m。

图1 智能车辆模型

传统蚁群算法的路径规划并没有考虑路径拐点的转弯半径，而车辆在行驶过程中为避免侧翻，需满足一定的转向特性，为此，本文在改进传统蚁群算法路径选择概率和信息素更新方式的基础上，再通过样条插值方法对规划路径进行平滑处理，使得其转向半径满足公式(10)，从而确保车辆行驶的稳定性。

综上所述，改进后的蚁群算法基本流程如图2所示。

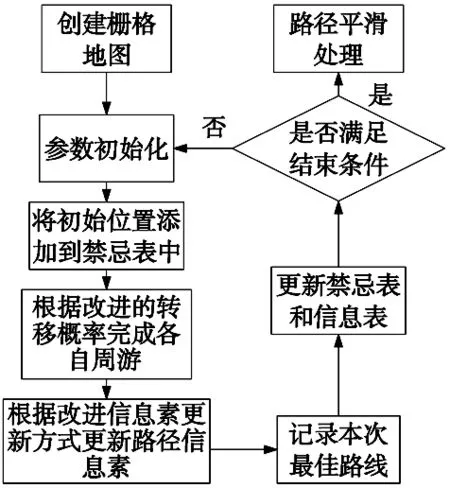
图2 改进蚁群算法流程图

3 仿真实验

为验证本文所提改进蚁群路径规划算法的有效性，以智能车为对象，采用栅格地图环境进行对比仿真实验。

3.1 栅格地图环境创建

在栅格地图中，分别通过用0和1表示可行区域和障碍物区域，为充分验证本文所提算法的有效性，分别创建如图3a所示的20×20的静态方格地图，以下称为1号地图，该地图中仅存在静态障碍物，以及如图3b所示的11×15的动态车道地图，以下称为2号地图，该地图存在静态和动态两种障碍物。

(a) 1号静态方格地图

(b) 2号动态车道地图图3 栅格地图环境

图中，黑色方格表示静态障碍物以及车道边界等不可行区域，红色方格代表起点，蓝色方格代表终点，黄色方格代表动态障碍物，其沿x轴方向移动。

3.2 仿真运行结果

分别使用传统蚁群算法和本文改进蚁群算法在1号地图和2号地图进行仿真实验，仿真参数设置为：蚂蚁个数M为50，迭代次数K为100，信息素全局蒸发系数为0.8，信息素局部蒸发系数λ为0.6，重要程度参数α为2，β为4，信息素强度Q为2。得到仿真结果如图4～图6所示。

1号地图仿真结果如图4所示。

(a) 传统蚁群算法路径规划结果

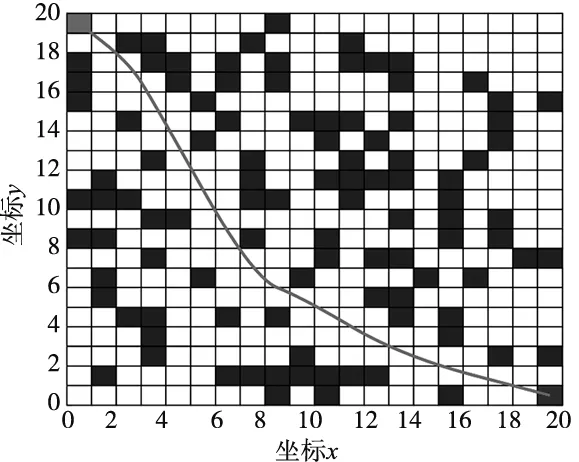
(b) 本文改进蚁群算法路径规划结果图4 1号地图中仿真结果

表1 1号地图仿真结果数据

分析1号地图两种算法仿真结果，从图4a中可以看出，传统蚁群算法可有效避开已知静态障碍物，而规划出一条全局路径；从图4b中可以看出，本文改进的蚁群算法能够有效避开图中静态障碍物，且规划出的路径相对较为平滑；从表1所示的仿真结果对比中可以看出，改进蚁群算法较传统蚁群算法最优路径长度减少了17.5%，运行时间减少了75.8%。

1号地图两组仿真实验重点证明了改进算法在收敛速度和全局优化上较传统算法具有明显的优越性。

2号地图仿真结果如图5所示。

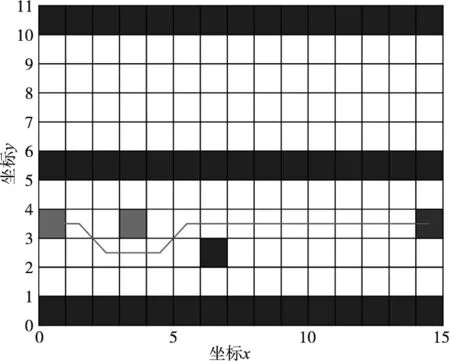
(a) 初始状态路径规划结果

(b) 动态障碍位置变化后路径规划结果图5 2号地图中传统蚁群算法仿真结果

分析2号地图传统蚁群算法仿真结果，从图5可以看出，初始状态时该算法能够较好的同时避开动态和静态障碍物，而当动态障碍物位置发生变化时，由于算法中的路径选择概论并没有对动态障碍物位置信息进行更新，所以路径规划结果不会发生变化，无法有效避开位置更新后的动态障碍物。

分析2号地图改进蚁群算法仿真结果，从图6可以看出，初始状态时该算法能够较好的同时避开动态和静态障碍物，当动态障碍物位置发生变化时，由于改进算法中的路径选择概率引入了动态障碍物位置信息，因而能根据动态障碍的实时位置进行路径规划，从而有效避开动态障碍物，且规划出的路径平滑性较好。

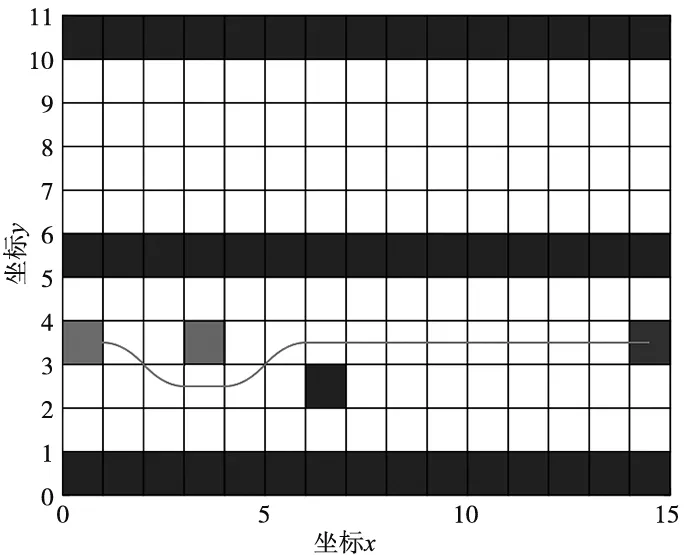
(a) 初始状态路径规划结果

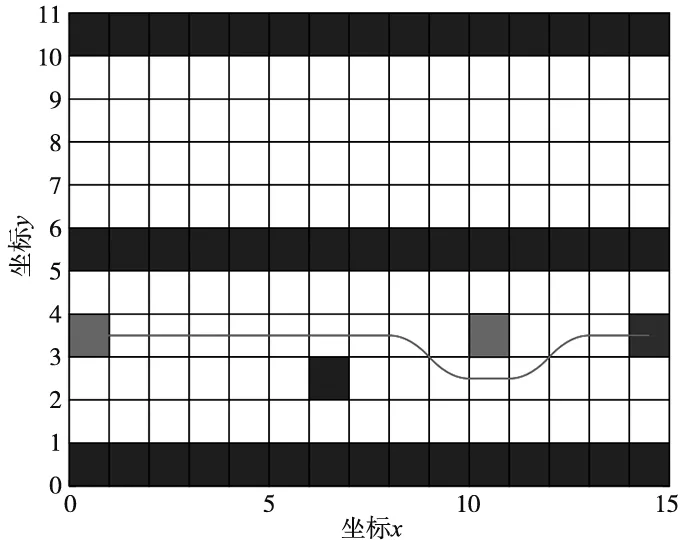
(b) 动态障碍位置变化后路径规划结果图6 2号地图中改进蚁群算法仿真结果

2号地图两组仿真实验结果重点证明了改进算法在动态避障以及路径平滑上较传统算法具有明显优越性。

4 结论

本文针对智能车辆路径规划问题，提出一种改进蚁群智能路径规划方法，较好的解决了传统蚁群算法搜索时间长和容易陷入局部最优等缺陷，在提高算法效率的同时保证了路径的平滑性并能实现实时动态避障，进一步提高了车辆行驶的安全性。两种不同工况下的对比仿真实验充分验证了所提改进蚁群算法具有以下优越性：一是通过在概率转移公式中引入障碍物位置信息，实现了动态避障；二是通过改进信息素更新方式，提高了算法的收敛性；三是通过样条插值方法提高了路径的平滑性。