基于指定聚类数目AP算法的滚动轴承故障诊断*

杨庆勇，刘雪涛，倪 伟，徐 飞，蒋占四

(桂林电子科技大学机电工程学院，广西 桂林 541004)

0 引言

旋转机械故障诊断是机械故障诊断十分重要的内容。由于旋转机械设备复杂，机械系统的故障研究受到了很大的限制，当前旋转机械的故障诊断研究大多针对其关键零部件轴承和齿轮[1]。传统的旋转机械故障诊断是基于信号时频分析，如快速傅里叶变换、短时傅里叶变换、Wigner-Ville分布、小波变换、经验模态分解等信号时频分析方法都具有各自的适用范围[2]。近十几年来，随着大数据和人工智能技术的发展，基于模式识别的故障诊断技术得到了充分的发展，支持向量机、BP神经网络[3]、深度学习[4-5]、聚类分析[6-7]等方法广泛的应用到机械故障诊断领域，推动了智能故障诊断技术的发展。

仿射传播聚类算法(AP)是2007年由Frey B J等提出的聚类算法[8]，经过十几年的发展和研究，已有很多改进的AP算法被提出。但AP算法具有局限性，在处理某些数据集会出现振荡不收敛，处理高维数据计算速度慢的情况[9]。众多学者对AP算法的研究和优化主要集中在偏向度(P)[10]、阻尼系数[11]和相似度矩阵(S)三方面[12-14]，有学者研究AP算法与其他聚类算法相结合的复合聚类算法[15-16 ]。Wang K等[17]提出一种自适应的AP算法，该算法首先生成不同数目的聚类结果，再比较各聚类结果的轮廓系数，选出轮廓系数最佳的聚类结果。Wei Z等[7]把AP算法应用到滚动轴承故障诊断中，取得了很好的效果，但AP算法中的P值需要人为调整来达到最佳的聚类精度。上述对于AP算法中P值的改进主要是如何快速地找到正确聚类数目下的P值，让聚类的过程耗时更短。根据研究可以发现，在很多数据集中不同的P值可以得到相同的聚类数目，对于如何在不同P值取得相同聚类数目的聚类结果集中选出最佳聚类结果少有研究。因此研究了一种指定聚类数目AP算法(SNAP)并应用在滚动轴承故障诊断领域中，该算法首先找出所有不同P值下聚类数目相同的聚类结果，通过对比聚类结果的轮廓系数，再挑选出轮廓系数大的聚类结果作为最终的聚类结果。

1 仿射传播聚类算法AP

1.1 AP算法原理

与一般聚类方法不一样的是，AP算法把所有的数据样本都看作潜在的聚类代表点，所有样本的初始权重都设置为一样。AP算法主要有相似度矩阵S、偏向度P、归属度A、吸引度R以及阻尼因子λ[18]。相似度矩阵S是样本间特征点之间的相似度，以欧式负距离来衡量，公式如下：

(1)

P是与聚类数目相关的参数，AP算法不需要事先知道样本类数，改变P就可以控制聚类数目；归属度A和吸引度R是两个传递信息的参数，AP算法的分类就是根据这两个参数来作为依据，先计算出候选类代表k能够作为数据i的类代表的吸引程度R(I，k) 和数据i认同数据k为类代表的归属程度A(i，k)，然后根据式(5)来判断，值越大，表明数据k作为最终聚类中心的可能性越大，不断循环迭代，直到超过初始化时设定的迭代次数最大值或者吸引度和归属度的值趋于稳定即收敛( 聚类数目确定)，只要满足其中一个条件即可停止。下面是归属度A和吸引度R的一些计算公式:

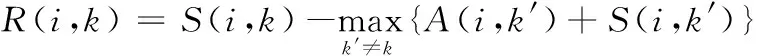
(2)

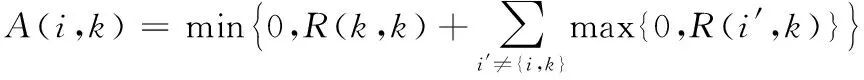
(3)

(4)

E(i,k)=A(i,k)+R(i,k)

(5)

阻尼因子是为了防止算法迭代不收敛，取值范围为[0.5,1]。

Rnew(i,k)=λRold(i,k)+(1-λ)Rnew(i,k)
Anew(i,k)=λAnew(i,k)+(1-λ)Anew(i,k)

(6)

运用AP算法进行聚类时，输入的是S与P，而且需要预先设置最大迭代数、阻尼因子等参数的初值，输出的是聚类的个数及索引向量。

1.2 AP算法中偏向度P存在的问题

由AP算法的原理可知，P是与聚类数目密切相关的一个参数，改变P，则得到的聚类数目可能会改变。图1是研究三类样本数据在不同的P值与聚类数目、聚类精度的关系。实验用到的AP算法相关参数设置：maxits=200;convits=50;lam=0.85;plt=0;details=0;nonoise=0。图中的横坐标是P取S的均值倍数，实验迭代了20个倍数，所用到的数据集由表1列出，Iris和Wine数据集由UCI机器学习数据库中下载得到，Bearing为机械综合故障模拟实验平台(MFS-MG)采集的滚动轴承数据集，在3.1节有详细介绍。

表1 实验数据集

由图1可知P的确影响着聚类的数目，不同P值得到相同聚类数目得聚类结果，其精度也有差异。以滚动轴承数据为例，偏向度倍数取2～6时，聚类的数目都为5类，与样本的实际分类一致，但分类的正确率有所变化，如表2所示。如何找出指定聚类数目下的最佳聚类结果，这是研究的重点。

图1 P值与聚类数目、聚类精度的关系

2 指定聚类数目AP算法

2.1 轮廓系数(SC)

在实际的聚类过程中，特征数据集的类别往往是未知的，基于内部簇类有效性指标是检验聚类结果最常用的方法[19]，采取轮廓系数(SC)来评价聚类的结果具有一定的优势。SC适用于实际类别信息未知的情况，取值范围[-1,1]，取值越大，簇的密度越高，聚类结果越好。计算公式如下：

(7)

(8)

式中，a(i) 表示样本i与它同类别中其它样本的平均距离，b(i)表示样本i与它距离最近不同类别中样本的平均距离。对于一个样本集合，所有样本轮廓系数的平均值就是这个样本的整体SC值。

2.2 指定聚类数目的AP算法(SNAP)

针对指定聚类数目的条件下，如何找到聚类数目与指定数目相等并且聚类精度最高的对应P的问题，设计出SNAP算法，该算法输入的是指定的聚类数目number及样本特征数据data，输出的是聚类精度最高的聚类结果。算法伪代码如表3所示，T表示P取几倍的相似度矩阵均值，即P=T×mean(S),AP算法默认P=mean(S)。算法可以分为三步走：第一步为不断改变P值，T每迭代一次加1，即P迭代的步长为S的均值。当聚类结果恰好等于指定的聚类数目时，记录下当前的T。第二步是找出聚类数目等于指定聚类数目的聚类结果，并且记录下每次聚类结果的SC值，当聚类结果数目小于指定聚类数目时，停止迭代。第三步是比较第二步记录下的SC值，选择SC值最大的聚类结果作为最终聚类结果。AP算法流程图见图2。

表3 算法伪代码

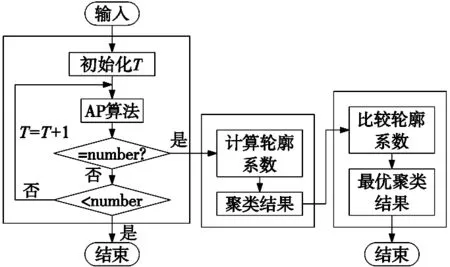
图2 指定聚类数目AP算法流程图

3 实验验证

3.1 滚动轴承故障实验数据与特征提取

实验数据采用美国Spectra Quest公司生产的机械综合故障模拟实验平台(MFS-MG)采集，主要结构如图3所示。

实验数据的获取、处理以及聚类特征的提取主要用文献[7]中提到的方法，在12.8 kMHz采样频率下采集了5种工况下的轴承振动数据，这5种工况分别是内圈故障、外圈故障、滚动体故障、保持架故障和正常的轴承。首先把5种工况的振动信号中间部分稳定信号各取30个样本数据，每个样本数据为2048个采样点的信号段，得到150个样本数据。再对每个样本数据提取时域、频域和能量3个方面的特征，首先对每个样本提取14种时频域特征，得到150×14的特征样本矩阵。

图3 机械综合故障模拟实验平台

每个样本进行小波包(WP)分解，对前8个分量进行时频域特征提取，得到150×112的特征样本矩阵；再对小波包分解的8个分量进行能量特征提取，得到150×8的特征样本矩阵；最后把三种特征整合到一起，得到150×134的总特征样本矩阵，这个特征矩阵就是聚类的输入特征矩阵。

图4 滚动轴承5个工况的部分振动信号图

3.2 滚动轴承故障数据聚类结果

由3.1节得到滚动轴承5个工况下的聚类特征样本矩阵150×134，总共150个样本，134个特征。把特征矩阵作为原AP算法的输入，相关参数maxits=200;convits=50;lam=0.85;plt=0;details=0;nonoise=0;偏向度也设置为默认P=mean(S)；得到的聚类结果如图5所示，实际样本只有5类，图示结果分类混乱，聚类数目明显增多。

当指定类数为5时，把指定类数5和特征矩阵作为SNAP算法的输入，当聚类数目小于指定聚类数目时，迭代停止，根据表4可知，P取2～6倍数的相似度均值时，聚类数目等于指定数目，P取3～4时，轮廓系数最大，其聚类准确度也最高，最佳聚类结果如图6a所示。当把滚动轴承5个工况下的样本数据划分为有故障的样本数据和正常的轴承数据时，即指定分类数目为2，输入分类数目2和特征矩阵，经过运算，不同的P得到的聚类结果一样，如图6b所示，类间差距明显，经过验证其准确率也是100%。

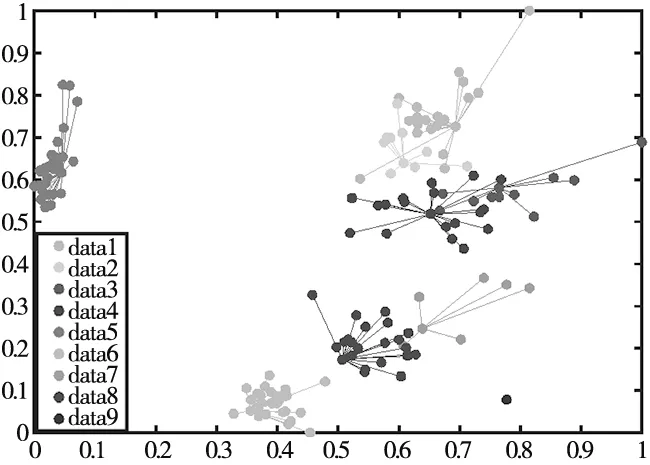
图5 默认偏向度下AP轴承数据聚类结果图

表4 相似度均值倍数(T)对聚类结果影响

(a) 指定聚类数目为5 (b) 指定聚类数目为2图6 指定聚类数目最佳聚类图

3.3 不同聚类算法结果的比较

为了验证所提算法的有效性，对三类数据集分别用K-means、K-medoids和AP进行处理，得出结果与SNAP处理所得结果进行比较。聚类结果的评价指标有ACC(精度)、SIL(轮廓系数)、AMI(互信息)和Num(聚类数目)，如表5所示。

表5 不同聚类算法对数据集处理结果比较

4 结论

针对指定聚类数目的AP聚类问题，研究了如何在指定聚类数目下，运行算法得到最佳聚类结果。提出指定聚类数目的AP算法(SNAP)，该算法需要输入所指定的聚类数目和样本特征矩阵，输出相对应的聚类数目的样本的标签。该算法的主要原理是首先找到指定聚类数目下不同偏向度的所有聚类结果，再通过比较所有聚类结果的轮廓系数，把轮廓系数最大的聚类结果作为最终聚类结果。通过三种真实数据在K-means、K-medoids 、AP和 SNAP不同聚类方法下的聚类结果比较，证明指定聚类数目AP聚类算法可行且准确率较高，并适用于未知标签的滚动轴承故障数据分类。聚类分析是机械智能故障诊断的一类重要方法，但并不是所有的聚类方法都可以直接应用到故障诊断上，SNAP算法为其他聚类分析方法在智能故障诊断上的应用提供新的改进思路。